Регулярные выражения (РВ) — это очень удобная форма записи так называемых регулярных или автоматных языков. Поэтому РВ используются в качестве входного языка во многих системах, обрабатывающих цепочки. Рассмотрим примеры таких систем:
В данной статье мы сначала ознакомимся с конечными автоматами и их видами (ДКА и НКА), и далее рассмотрим пример построения минимального ДКА по регулярному выражению.
Конечный автомат (КА) — это преобразователь, который позволяет сопоставить входу соответствующий выход, причем выход этот может зависеть не только от текущего входа, но и от того, что происходило раньше, от предыстории работы конечного автомата. Даже поведение человека, а не только искусственных систем можно описать с помощью КА. Например, ваша реакция на то что ваш сосед слушает громко музыку по ночам, будет одной после первого такого случая и совершенно другой после нескольких таких случаев. Таких предысторий может быть бесконечное число, возникает вопрос: какой памятью должен обладать КА, чтобы вести себя по разному для каждой предыстроии? Понятно, что хранить бесконечное число предысторий невозможно. Поэтому автомат как бы разбивает все возможные предыстории на классы эквивалентности. Две истории являются эквивалентными, если они одинаково влияют на поведение автомата в дальнейшем. Класс эквивалентности к которому автомат отнес свою текущую предысторию, называют еще внутренним состоянием автомата.
Рассмотрим пример работы примитивного КА:

Данный КА состоит из:
Считывающее устройство может двигаться в одном направлении, как правило слева на право, тем самым считывая символы входной цепочки. За каждое такое движение оно может считать один символ. Далее, считанный символ передается блоку управлений. Блок управления изменяет состояние автомата на основе правил переходов. Если список правил переходов не содержит правила для считанного символа, то автомат «умирает».
Теперь рассмотрим, какими способами можно задать КА. Они могут задаваться в виде графов или в виде управляющих таблиц. В виде графа КА задается следующим способом:
В виде управляющей таблицы, так:
Пример КА в виде графа и в виде управляющей таблицы будет представлен ниже.
Основное отличие ДКА и НКА состоит в том, что ДКА в процессе работы может находится только в одном состоянии, а НКА в нескольких состояниях одновременно. В качестве примера работы НКА можно привести идею американского физика Хью Эверетта от том, что любое событие разбивает мир на несколько миров, в каждом из которых это событие закончилось по-своему. Например, в одном мире Гитлер выиграл Вторую мировую войну, в другом – Ньютон вместо физики занялся бизнесом и открытие законов классической механики пришлось отложить лет на 50. Чтобы сделать какие-то выводы из работы автомата, следует изучить все «миры». После того как вся входная цепочка будет считана, мы полагаем, что НКА допускает данную цепочку, если он завершил работу в допускающем состоянии хотя бы в одном из множества «миров». Соответственно, автомат отвергает цепочку, если он завершил работу в недопускающем состоянии в каждом «мире». ДКА же принимает цепочку, это очевидно, если после считывания всей входной цепочки он оказывается в допускающем состоянии.
В большинстве случаев построить НКА гораздо проще чем ДКА. Но, не смотря на это использовать НКА для моделирования — не самая хорошая идея. К счастью, для каждого НКА можно построить ДКА, допускающий тот же входной язык. В данной статье мы не будем приводить алгоритм построения ДКА по НКА, а рассмотрим данный алгоритм на основе наглядного примера ниже.
Для начала приведем список операций РВ используемый в данной статье, в порядке их приоритетности:
Рассмотрим пример, дано регулярное выражение:
xy* (x | y*) | ab (x | y*) | (x | a*) (x | y*)
Нужно построить минимальный ДКА по регулярному выражению и продемонстрировать распознавание корректной и некорректной цепочки.
Для начала упростим данное РВ, используя правосторонний дистрибутивный закон конкатенации относительно объединения получаем следующее РВ:
(xy* | ab | (x | a*)) (x | y*)
Теперь строим автомат по данному РВ:

По правилу преобразования конкатенации (не будем приводить правила преобразования РВ в КА, так как они довольно очевидные), получаем следующий автомат:

По правилу преобразования объединения:

По правилу преобразования конкатенации:

И в конце применяем правило преобразования замыкания и получаем εНКА. Здесь нужно оговорится, что εНКА — это НКА, который содержит ε-переходы. В свою очередь ε-переход — это переход, при котором автомат не учитывает входную цепочку или другими словами переход по пустому символу.
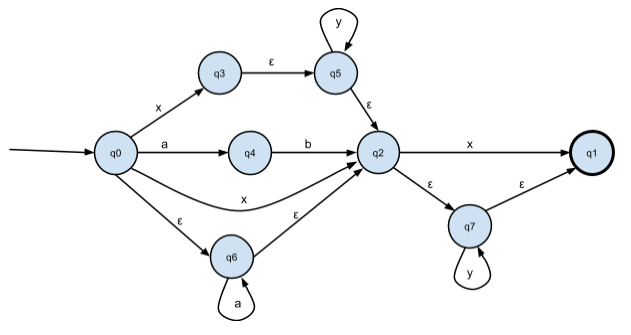
Избавляемся от ε-переходов («звездочкой» обозначены конечные состояния):
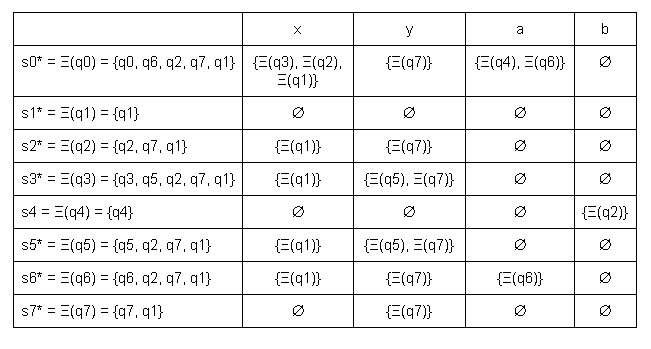
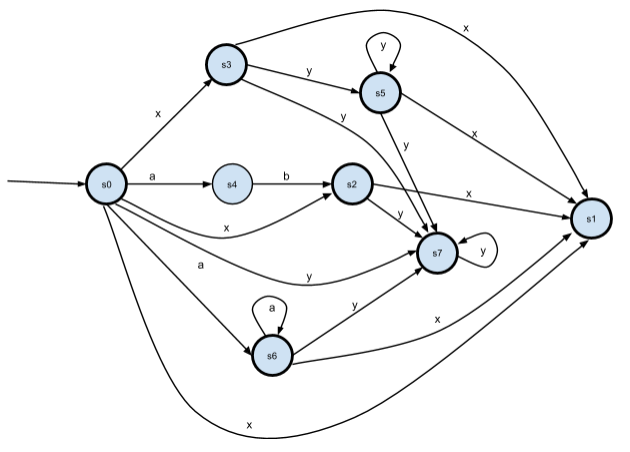
В данном НКА состояния s3 и s5 эквивалентны, так как δ(s3, x) = δ(s5, x) = s1 и δ(s3, y) = δ(s5, y) = s5, s7. Переименовываем состояния s6 -> s5 и s7 -> s6:
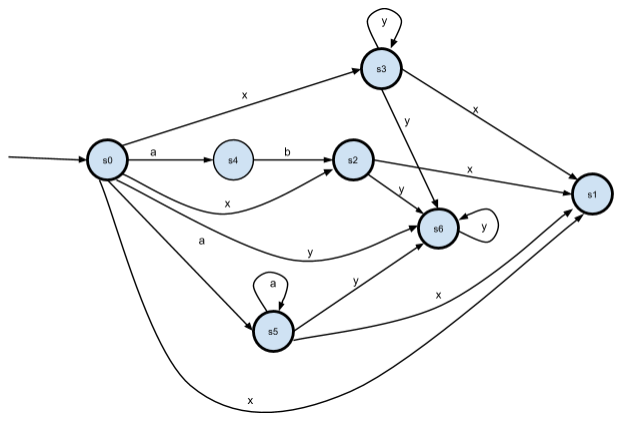
Строим ДКА по НКА:
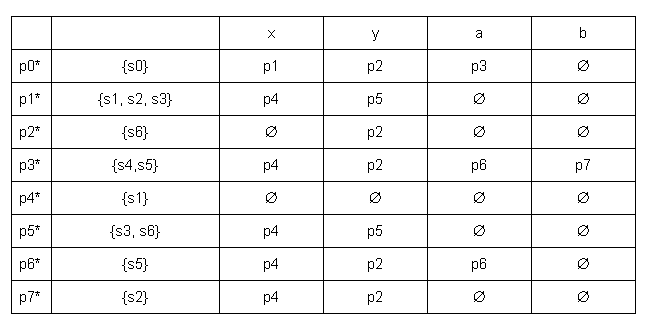

В данном ДКА состояния p1 и p5 эквивалентны, так как
δ(p1, x) = δ(p5, x) = p4 и δ(p1, y) = δ(p5, y) = p5. Переименовываем состояния p6 -> p5 и p7 -> p6:

Данный автомат является минимальным ДКА.
Пускай δ — функция переходов, то расширенную функцию переходов, построенную по δ, обозначим δ’, и ω — входная цепочка.
Допустим на вход подается цепочка ω = aaax, мы ожидаем, что автомат окажется в одном из допускающих состояний.
δ’(p0, ε) = p0
δ’(p0, a) = δ(δ’(p0, ε), a) = δ(p0, a) = p3
δ’(p0, aa) = δ(δ’(p0, a), a) = δ(p3, a) = p5
δ’(p0, aaa) = δ(δ’(p0, aa), a) = δ(p5, a) = p5
δ’(p0, aaax) = δ(δ’(p0, aaa), x) = δ(p5, x) = p4
p4 — допустимое конечное состояние, таким образом цепочка aaax является корректной для данного автомата.
Теперь допустим, что ω = xyyb:
δ’(p0, ε) = p0
δ’(p0, x) = δ(δ’(p0, ε), x) = δ(p0, x) = p1
δ’(p0, xy) = δ(δ’(p0, x), y) = δ(p1, y) = p1
δ’(p0, xyy) = δ(δ’(p0, xy), y) = δ(p1, y) = p1
δ’(p0, xyyb) = δ(δ’(p0, xyy), b) = δ(p1, b) = ∅
Здесь мы видим, что если подать на вход автомату символ b, когда он находится в состоянии p1, то данный автомат умрет, следовательно цепочка xyyb — некорректна.
P. S. В данной статье был рассмотрен алгоритм построение ДКА по РВ, но существуют более удобные алгоритмы, в частности для программирования, но это уже тема для другой статьи…
- Команда grep операционной системы Unix или аналогичные команды для поиска цепочек, которые можно встретить в Web-броузерах или системах форматирования текста. В таких системах РВ используются для описания шаблонов, которые пользователь ищет в файле. Различные поисковые системы преобразуют РВ либо в детерминированный конечный автомат (ДКА), либо недетерминированный конечный автомат (НКА) и применяют этот автомат к файлу, в котором производится поиск.
- Генераторы лексических анализаторов. Лексические анализаторы являются компонентом компилятора, они разбивают исходную программу на логические единицы (лексемы), которые могут состоять из одного или нескольких символов и имеют определенный смысл. Генератор лексических анализаторов получает формальные описания лексем, являющиеся по существу РВ, и создает ДКА, который распознает, какая из лексем появляется на его входе.
- РВ в языках программирования.
В данной статье мы сначала ознакомимся с конечными автоматами и их видами (ДКА и НКА), и далее рассмотрим пример построения минимального ДКА по регулярному выражению.
Конечные автоматы
Конечный автомат (КА) — это преобразователь, который позволяет сопоставить входу соответствующий выход, причем выход этот может зависеть не только от текущего входа, но и от того, что происходило раньше, от предыстории работы конечного автомата. Даже поведение человека, а не только искусственных систем можно описать с помощью КА. Например, ваша реакция на то что ваш сосед слушает громко музыку по ночам, будет одной после первого такого случая и совершенно другой после нескольких таких случаев. Таких предысторий может быть бесконечное число, возникает вопрос: какой памятью должен обладать КА, чтобы вести себя по разному для каждой предыстроии? Понятно, что хранить бесконечное число предысторий невозможно. Поэтому автомат как бы разбивает все возможные предыстории на классы эквивалентности. Две истории являются эквивалентными, если они одинаково влияют на поведение автомата в дальнейшем. Класс эквивалентности к которому автомат отнес свою текущую предысторию, называют еще внутренним состоянием автомата.
Рассмотрим пример работы примитивного КА:

Данный КА состоит из:
- ленты, представленной входной цепочкой.
- считывающее устройство.
- блок управления, который содержит список правил переходов.
Считывающее устройство может двигаться в одном направлении, как правило слева на право, тем самым считывая символы входной цепочки. За каждое такое движение оно может считать один символ. Далее, считанный символ передается блоку управлений. Блок управления изменяет состояние автомата на основе правил переходов. Если список правил переходов не содержит правила для считанного символа, то автомат «умирает».
Теперь рассмотрим, какими способами можно задать КА. Они могут задаваться в виде графов или в виде управляющих таблиц. В виде графа КА задается следующим способом:
- вершины графа, соответствуют состояниям КА.
- направленные ребра, соответствуют функциям переходов (возле каждого такое ребра указывается символ, по которому выполняется переход).
- вершина с входящим в него ребром, которое не выходит не из одного состояния, соответствует начальному состоянию.
- конечные состояния КА помечаются жирным контуром.
В виде управляющей таблицы, так:
- состояния КА располагаются в строках таблицы.
- символы распознаваемого языка — в столбцах.
- на пересечении указывается состояние в которое можно попасть из данного состояния по данному символу.
Пример КА в виде графа и в виде управляющей таблицы будет представлен ниже.
ДКА и НКА
Основное отличие ДКА и НКА состоит в том, что ДКА в процессе работы может находится только в одном состоянии, а НКА в нескольких состояниях одновременно. В качестве примера работы НКА можно привести идею американского физика Хью Эверетта от том, что любое событие разбивает мир на несколько миров, в каждом из которых это событие закончилось по-своему. Например, в одном мире Гитлер выиграл Вторую мировую войну, в другом – Ньютон вместо физики занялся бизнесом и открытие законов классической механики пришлось отложить лет на 50. Чтобы сделать какие-то выводы из работы автомата, следует изучить все «миры». После того как вся входная цепочка будет считана, мы полагаем, что НКА допускает данную цепочку, если он завершил работу в допускающем состоянии хотя бы в одном из множества «миров». Соответственно, автомат отвергает цепочку, если он завершил работу в недопускающем состоянии в каждом «мире». ДКА же принимает цепочку, это очевидно, если после считывания всей входной цепочки он оказывается в допускающем состоянии.
В большинстве случаев построить НКА гораздо проще чем ДКА. Но, не смотря на это использовать НКА для моделирования — не самая хорошая идея. К счастью, для каждого НКА можно построить ДКА, допускающий тот же входной язык. В данной статье мы не будем приводить алгоритм построения ДКА по НКА, а рассмотрим данный алгоритм на основе наглядного примера ниже.
Построение минимального ДКА по регулярному выражению
Для начала приведем список операций РВ используемый в данной статье, в порядке их приоритетности:
- итерация (замыкание Клини), с помощью символа "*"
- конкатенация задается с помощью пробела или пустой строки (например: ab)
- объединение, с помощью символа "|"
Рассмотрим пример, дано регулярное выражение:
xy* (x | y*) | ab (x | y*) | (x | a*) (x | y*)
Нужно построить минимальный ДКА по регулярному выражению и продемонстрировать распознавание корректной и некорректной цепочки.
Для начала упростим данное РВ, используя правосторонний дистрибутивный закон конкатенации относительно объединения получаем следующее РВ:
(xy* | ab | (x | a*)) (x | y*)
Теперь строим автомат по данному РВ:

По правилу преобразования конкатенации (не будем приводить правила преобразования РВ в КА, так как они довольно очевидные), получаем следующий автомат:

По правилу преобразования объединения:

По правилу преобразования конкатенации:

И в конце применяем правило преобразования замыкания и получаем εНКА. Здесь нужно оговорится, что εНКА — это НКА, который содержит ε-переходы. В свою очередь ε-переход — это переход, при котором автомат не учитывает входную цепочку или другими словами переход по пустому символу.

Избавляемся от ε-переходов («звездочкой» обозначены конечные состояния):


В данном НКА состояния s3 и s5 эквивалентны, так как δ(s3, x) = δ(s5, x) = s1 и δ(s3, y) = δ(s5, y) = s5, s7. Переименовываем состояния s6 -> s5 и s7 -> s6:

Строим ДКА по НКА:


В данном ДКА состояния p1 и p5 эквивалентны, так как
δ(p1, x) = δ(p5, x) = p4 и δ(p1, y) = δ(p5, y) = p5. Переименовываем состояния p6 -> p5 и p7 -> p6:

Данный автомат является минимальным ДКА.
Пускай δ — функция переходов, то расширенную функцию переходов, построенную по δ, обозначим δ’, и ω — входная цепочка.
Допустим на вход подается цепочка ω = aaax, мы ожидаем, что автомат окажется в одном из допускающих состояний.
δ’(p0, ε) = p0
δ’(p0, a) = δ(δ’(p0, ε), a) = δ(p0, a) = p3
δ’(p0, aa) = δ(δ’(p0, a), a) = δ(p3, a) = p5
δ’(p0, aaa) = δ(δ’(p0, aa), a) = δ(p5, a) = p5
δ’(p0, aaax) = δ(δ’(p0, aaa), x) = δ(p5, x) = p4
p4 — допустимое конечное состояние, таким образом цепочка aaax является корректной для данного автомата.
Теперь допустим, что ω = xyyb:
δ’(p0, ε) = p0
δ’(p0, x) = δ(δ’(p0, ε), x) = δ(p0, x) = p1
δ’(p0, xy) = δ(δ’(p0, x), y) = δ(p1, y) = p1
δ’(p0, xyy) = δ(δ’(p0, xy), y) = δ(p1, y) = p1
δ’(p0, xyyb) = δ(δ’(p0, xyy), b) = δ(p1, b) = ∅
Здесь мы видим, что если подать на вход автомату символ b, когда он находится в состоянии p1, то данный автомат умрет, следовательно цепочка xyyb — некорректна.
P. S. В данной статье был рассмотрен алгоритм построение ДКА по РВ, но существуют более удобные алгоритмы, в частности для программирования, но это уже тема для другой статьи…