Нам нужно реализовать детектор лжи, который по подрагиванию рук человека, определяет, говорит он правду или нет. Допустим, когда человек лжет, руки трясутся чуть больше. Сигнал может быть таким:

Интересный метод, описан в статье «A Tutorial on Hidden Markov Models and Selected Applications in Speech Recognition» L.R. Rabiner, которая вводит модель скрытой цепи Маркова и описывает три ценных алгоритма: The Forward-Backward Procedure, Viterbi Algorithm и Baum-Welch reestimation. Несмотря на то, что эти алгоритмы представляют интерес только в совокупности, для большего понимания описывать их лучше по отдельности.
Метод скрытых цепей Маркова имеет широкое применение, например, он используется для поиска CG-островков (участков DNA, RNA с высокой плотностью связки цитозина и гуанина), в то время как сам Лоренс Рабинер использовал его для распознавания речи. Мне алгоритмы пригодились для того, чтобы отслеживать смену стадий сна/бодрствования по электроэнцефалограмме и искать эпилептические припадки.
В модели скрытых цепей Маркова предполагается, что рассматриваемая система обладает следующими свойствами:
Модель HMM можно описать как: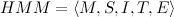
Время t предполагается дискретным, заданным неотрицательными целыми числами, где 0 соответствует начальному моменту времени, а Tm наибольшему значению.
Когда у нас 2 скрытых состояния, и наблюдаемые величины подчиняются нормальному распределению с различными дисперсиями, как в примере с детектором лжи, для каждого из состояний алгоритм функционирования системы можно изобразить вот так:
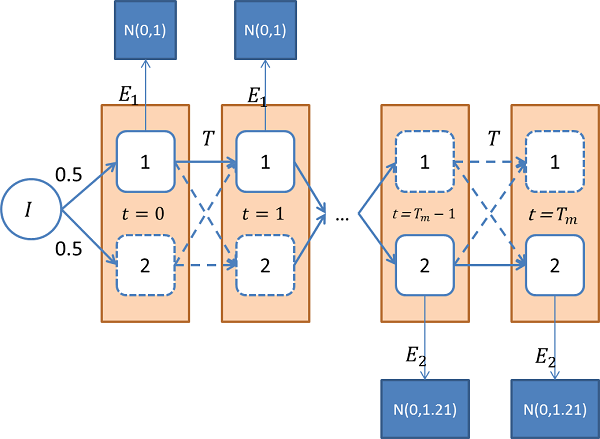
Более простое описание уже упоминалось в Вероятностные модели: примеры и картинки.
Выбор вектора распределений наблюдаемых величин зачастую лежит на исследователе. В идеале наблюдаемая величина и есть скрытое состояние, и задача определения этих состояний в таком случае становится тривиальной. В реальности все сложнее, например, классическая модель, описанная Рабинером, предполагает, что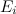 – конечное дискретное распределение. Что-то вроде того, что на графике ниже:
– конечное дискретное распределение. Что-то вроде того, что на графике ниже:
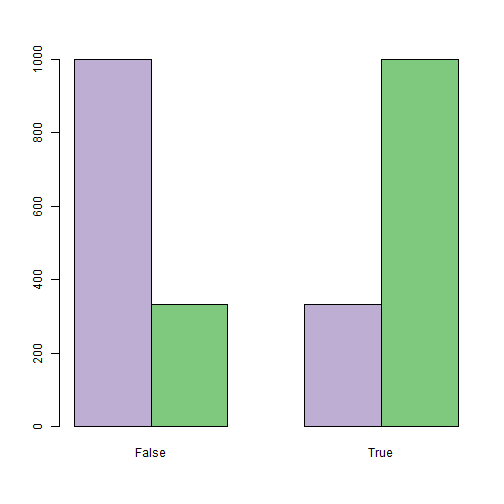
У исследователя, обычно, есть свобода в выборе распределения наблюдаемых состояний. Чем сильнее наблюдаемые величины различают скрытые состояния тем лучше. С точки зрения программирования, перебор различных наблюдаемых характеристик означает необходимость аккуратной инкапсуляции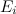 . На графике ниже приведен пример исходных данных для задачи о детекторе лжи, где распределение наблюдаемой характеристики (подрагивания рук) непрерывное, так как моделировалось как нормальное с средним 0 для обоих состояний, с дисперсией равной 1, когда человек говорит правду (фиолетовые столбцы) и 1.21, когда лжет (зеленые столбцы):
. На графике ниже приведен пример исходных данных для задачи о детекторе лжи, где распределение наблюдаемой характеристики (подрагивания рук) непрерывное, так как моделировалось как нормальное с средним 0 для обоих состояний, с дисперсией равной 1, когда человек говорит правду (фиолетовые столбцы) и 1.21, когда лжет (зеленые столбцы):

Для того, чтобы не касаться вопросов настройки модели, рассмотрим упрощенную задачу.
Дано:
два скрытых состояния, где честному поведению соответствует белый шум с дисперсией 1, лжи – белый шум с дисперсией 1.21;
выборка из 10 000 последовательных наблюдений o;
смена состояний происходит в среднем раз в 2 500 тактов.
Требуется определить моменты смены состояний.
Решение:
Зададим пятерку параметров модели:
Найдем наиболее правдоподобные состояния для каждого момента времени с помощью алгоритма Витерби при заданных параметрах модели.
Решение задачи сводится к заданию модели и прогону алгоритма Витерби.
По модели скрытых цепей Маркова и выборке значений наблюдаемых характеристик найдем такую последовательность состояний, которая наилучшим образом описала бы выборку в заданной модели. Понятие наилучшим образом можно трактовать по-разному, но устоявшимся решением является алгоритм Витерби, который находит такую последовательность , что
, что  .
.
Задача поиска решается с помощью динамического программирования, для этого рассмотрим функцию:
решается с помощью динамического программирования, для этого рассмотрим функцию:

где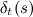 — наибольшая вероятность оказаться в состоянии s в момент времени t. Рекурсивно, эту функцию можно определить следующим образом:
— наибольшая вероятность оказаться в состоянии s в момент времени t. Рекурсивно, эту функцию можно определить следующим образом:
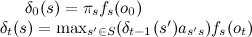
Одновременно с расчетом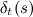 для каждого момента времени запоминаем наиболее вероятное состояние, из которого мы пришли, то есть
для каждого момента времени запоминаем наиболее вероятное состояние, из которого мы пришли, то есть 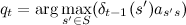 , на котором был достигнут максимум. При этом
, на котором был достигнут максимум. При этом 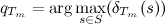 , и значит, можно восстановить
, и значит, можно восстановить 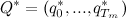 , пройдясь по ним в обратном порядке. Можно заметить, что
, пройдясь по ним в обратном порядке. Можно заметить, что 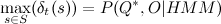 – значение искомой вероятности. Требуемая последовательность
– значение искомой вероятности. Требуемая последовательность  найдена. Интересным свойством алгоритма является, то что оценочная функция наблюдаемых характеристик входит в
найдена. Интересным свойством алгоритма является, то что оценочная функция наблюдаемых характеристик входит в 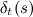 в виде сомножителя. Если считать, что
в виде сомножителя. Если считать, что 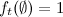 , то в случае пропусков в наблюдениях, все равно можно оценить наиболее вероятные скрытые состояния в эти моменты.
, то в случае пропусков в наблюдениях, все равно можно оценить наиболее вероятные скрытые состояния в эти моменты.
«Псевдокод» для алгоритма Витерби набросан ниже. Необходимо учесть, что все операции с векторами и матрицами поэлементные.
Кто-нибудь мог узнать в этом “псевдокоде” код на R, но это далеко не самая лучшая реализация.
Сравним периоды постоянства состояний, которые были заданы при моделировании (верхняя часть графика), и те, которые были найдены с помощью алгоритма Витерби (нижняя часть графика):

Вполне достойно по-моему, но каждый раз на такое не стоит надеяться.
Описанный ранее алгоритм Витерби требует определения модели скрытой цепи Маркова (Аргументов функции viterbi). Для их задания используется простая инициализация, которая подразумевает, что кроме выборки наблюдаемых величин O так же задана соответствующая им выборка скрытых состояний Q, которые откуда-то нам известны. В таком случае формулы для оценки параметров будут выглядеть следующим образом:
![S\leftarrow \left\{s:q_t=s,t\in[0,T_m]\right\} \\ M\leftarrow \|S\| \\ I\leftarrow \left(\frac{\sum_{t\in[0,T_m]}Id(q_t=s)}{T_m+1}, s\in S\right) \\ T\leftarrow \left(\frac{\sum_{t\in[1,T_m]}Id(q_{t-1}=s',q_t=s)}{\sum_{t\in[0,T_m]}(\sum_{t\in[1,T_m]}Id(q_{t-1}=s')}, s,s'\in S\right) \\ E\leftarrow \left(f_s(o_t)=\frac{\sum_{t\in [0,T_m]}Id(q_t=s,o_t=e)}{\sum_{t\in[0,T_m]}Id(q_t=s)}, s\in S\right)](http://mathurl.com/ark5aup.png)
где Id(x) – индикаторная функция,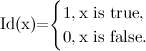
Для рассмотренного примера о детекторе лжи алгоритм неправильно классифицировал 413 из 10 000 состояний (~4%), что вовсе не плохо. Алгоритм Витерби способен с хорошей точностью детектировать моменты смены скрытых состояний, но только в случае, если распределения наблюдаемых характеристик точно известны. Если же известен только параметрический класс таких распределений, то существует способ выбора наиболее подходящих параметров, называемый алгоритм Баума-Велша.
Если интересно, требуйте продолжения…

Интересный метод, описан в статье «A Tutorial on Hidden Markov Models and Selected Applications in Speech Recognition» L.R. Rabiner, которая вводит модель скрытой цепи Маркова и описывает три ценных алгоритма: The Forward-Backward Procedure, Viterbi Algorithm и Baum-Welch reestimation. Несмотря на то, что эти алгоритмы представляют интерес только в совокупности, для большего понимания описывать их лучше по отдельности.
Метод скрытых цепей Маркова имеет широкое применение, например, он используется для поиска CG-островков (участков DNA, RNA с высокой плотностью связки цитозина и гуанина), в то время как сам Лоренс Рабинер использовал его для распознавания речи. Мне алгоритмы пригодились для того, чтобы отслеживать смену стадий сна/бодрствования по электроэнцефалограмме и искать эпилептические припадки.
В модели скрытых цепей Маркова предполагается, что рассматриваемая система обладает следующими свойствами:
- в каждый период времени система может находится в одном из конечного набора состояний;
- система случайно переходит из одного состояния в другое (возможно, в то же самое) и вероятность перехода зависит только от того состояния, в котором она находилась;
- в каждый момент времени система выдает одно значение наблюдаемой характеристики – случайную величину, зависящую только от текущего состояния системы.
Модель HMM можно описать как:
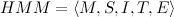
- M – число состояний;
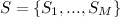 – конечное множество состояний;
– конечное множество состояний;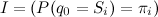 – вектор вероятностей, того что система находится в состоянии i в момент времени 0;
– вектор вероятностей, того что система находится в состоянии i в момент времени 0;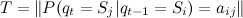 – матрица вероятностей перехода из состояния i в состояние j для
– матрица вероятностей перехода из состояния i в состояние j для ![\forall t\in[1,T_m]](https://habrastorage.org/r/w1560/getpro/habr/post_images/f35/bc4/b80/f35bc4b80fe1243b2277ae615cd731cb.png) ;
; ,
, 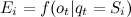 – вектор распределений наблюдаемых случайных величин, соответствующих каждому из состояний, заданных как функции плотности или распределения, определенные на O (совокупности наблюдаемых значений для всех состояний).
– вектор распределений наблюдаемых случайных величин, соответствующих каждому из состояний, заданных как функции плотности или распределения, определенные на O (совокупности наблюдаемых значений для всех состояний).
Время t предполагается дискретным, заданным неотрицательными целыми числами, где 0 соответствует начальному моменту времени, а Tm наибольшему значению.
Когда у нас 2 скрытых состояния, и наблюдаемые величины подчиняются нормальному распределению с различными дисперсиями, как в примере с детектором лжи, для каждого из состояний алгоритм функционирования системы можно изобразить вот так:

Более простое описание уже упоминалось в Вероятностные модели: примеры и картинки.
Выбор вектора распределений наблюдаемых величин зачастую лежит на исследователе. В идеале наблюдаемая величина и есть скрытое состояние, и задача определения этих состояний в таком случае становится тривиальной. В реальности все сложнее, например, классическая модель, описанная Рабинером, предполагает, что
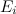 – конечное дискретное распределение. Что-то вроде того, что на графике ниже:
– конечное дискретное распределение. Что-то вроде того, что на графике ниже:
У исследователя, обычно, есть свобода в выборе распределения наблюдаемых состояний. Чем сильнее наблюдаемые величины различают скрытые состояния тем лучше. С точки зрения программирования, перебор различных наблюдаемых характеристик означает необходимость аккуратной инкапсуляции
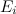 . На графике ниже приведен пример исходных данных для задачи о детекторе лжи, где распределение наблюдаемой характеристики (подрагивания рук) непрерывное, так как моделировалось как нормальное с средним 0 для обоих состояний, с дисперсией равной 1, когда человек говорит правду (фиолетовые столбцы) и 1.21, когда лжет (зеленые столбцы):
. На графике ниже приведен пример исходных данных для задачи о детекторе лжи, где распределение наблюдаемой характеристики (подрагивания рук) непрерывное, так как моделировалось как нормальное с средним 0 для обоих состояний, с дисперсией равной 1, когда человек говорит правду (фиолетовые столбцы) и 1.21, когда лжет (зеленые столбцы):
Для того, чтобы не касаться вопросов настройки модели, рассмотрим упрощенную задачу.
Дано:
два скрытых состояния, где честному поведению соответствует белый шум с дисперсией 1, лжи – белый шум с дисперсией 1.21;
выборка из 10 000 последовательных наблюдений o;
смена состояний происходит в среднем раз в 2 500 тактов.
Требуется определить моменты смены состояний.
Решение:
Зададим пятерку параметров модели:
- число состояний M=2;
- S={1,2};
- опыт показывает, что начальное распределение практически не имеет значения, поэтому I=(0.5,0.5);
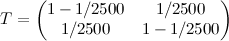 ;
;- E=(N(0,1),N(0,1.21)).
Найдем наиболее правдоподобные состояния для каждого момента времени с помощью алгоритма Витерби при заданных параметрах модели.
Решение задачи сводится к заданию модели и прогону алгоритма Витерби.
По модели скрытых цепей Маркова и выборке значений наблюдаемых характеристик найдем такую последовательность состояний, которая наилучшим образом описала бы выборку в заданной модели. Понятие наилучшим образом можно трактовать по-разному, но устоявшимся решением является алгоритм Витерби, который находит такую последовательность
 , что
, что  .
.Задача поиска
 решается с помощью динамического программирования, для этого рассмотрим функцию:
решается с помощью динамического программирования, для этого рассмотрим функцию:
где
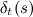 — наибольшая вероятность оказаться в состоянии s в момент времени t. Рекурсивно, эту функцию можно определить следующим образом:
— наибольшая вероятность оказаться в состоянии s в момент времени t. Рекурсивно, эту функцию можно определить следующим образом: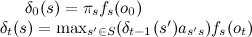
Одновременно с расчетом
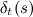 для каждого момента времени запоминаем наиболее вероятное состояние, из которого мы пришли, то есть
для каждого момента времени запоминаем наиболее вероятное состояние, из которого мы пришли, то есть 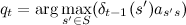 , на котором был достигнут максимум. При этом
, на котором был достигнут максимум. При этом 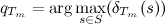 , и значит, можно восстановить
, и значит, можно восстановить 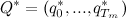 , пройдясь по ним в обратном порядке. Можно заметить, что
, пройдясь по ним в обратном порядке. Можно заметить, что 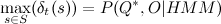 – значение искомой вероятности. Требуемая последовательность
– значение искомой вероятности. Требуемая последовательность  найдена. Интересным свойством алгоритма является, то что оценочная функция наблюдаемых характеристик входит в
найдена. Интересным свойством алгоритма является, то что оценочная функция наблюдаемых характеристик входит в 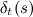 в виде сомножителя. Если считать, что
в виде сомножителя. Если считать, что 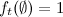 , то в случае пропусков в наблюдениях, все равно можно оценить наиболее вероятные скрытые состояния в эти моменты.
, то в случае пропусков в наблюдениях, все равно можно оценить наиболее вероятные скрытые состояния в эти моменты.«Псевдокод» для алгоритма Витерби набросан ниже. Необходимо учесть, что все операции с векторами и матрицами поэлементные.
Tm<-10000 # Max time
M<-2 # Number of states
S<-seq(from=1, to=M) # States [1,2]
I<-rep(1./M, each=M) # Initial distribution [0.5, 0.5]
T<-matrix(c(1-4./Tm, 4./Tm, 4./Tm,1-4./Tm),2) #[0.9995 0.0005; 0.0005 0.9995]
P<-c(function(o){dnorm(o)}, function(o){dnorm(o,sd=1.1)}) # Vector of density functions for each state (N(0,1), N(0,1.21))
E<-function(P,s,o){P[[s]](o)} # Calculate probability of observed value o for state s.
Es<-function(E,P,o) {
# Same for all states
probs<-c()
for(s in S) {
probs<-append(probs, E(P,s,o))
}
return(probs)
}
viterbi<-function(S,I,T,P,E,O,tm) {
delta<-I*Es(E,P,O[1]) # initialization for t=1
prev_states<-cbind(rep(0,length(S))) # zeros
for(t in 2:Tm) {
m<-matrix(rep(delta,length(S)),length(S))*T # delta(s')*T[ss'] forall s,s'
md<-apply(m,2,max) # search for max delta(s) by s' for all s
max_delta<-apply(m,2,which.max)
prev_states<-cbind(prev_states,max_delta)
delta<-md*Es(E,P,O[t]) # prepare next step delta(s)
}
return(list(delta=delta,ps=prev_states)) # return delta_Tm(s) and paths
}
restoreStates<-function(d,prev_states) {
idx<-which.max(d)
s<-c(idx)
sz<-length(prev_states[1,])
for(i in sz:2) {
idx<-prev_states[idx,i]
s<-append(s,idx,after=0)
}
return (as.vector(s))
}
Кто-нибудь мог узнать в этом “псевдокоде” код на R, но это далеко не самая лучшая реализация.
Сравним периоды постоянства состояний, которые были заданы при моделировании (верхняя часть графика), и те, которые были найдены с помощью алгоритма Витерби (нижняя часть графика):

Вполне достойно по-моему, но каждый раз на такое не стоит надеяться.
Описанный ранее алгоритм Витерби требует определения модели скрытой цепи Маркова (Аргументов функции viterbi). Для их задания используется простая инициализация, которая подразумевает, что кроме выборки наблюдаемых величин O так же задана соответствующая им выборка скрытых состояний Q, которые откуда-то нам известны. В таком случае формулы для оценки параметров будут выглядеть следующим образом:
![S\leftarrow \left\{s:q_t=s,t\in[0,T_m]\right\} \\ M\leftarrow \|S\| \\ I\leftarrow \left(\frac{\sum_{t\in[0,T_m]}Id(q_t=s)}{T_m+1}, s\in S\right) \\ T\leftarrow \left(\frac{\sum_{t\in[1,T_m]}Id(q_{t-1}=s',q_t=s)}{\sum_{t\in[0,T_m]}(\sum_{t\in[1,T_m]}Id(q_{t-1}=s')}, s,s'\in S\right) \\ E\leftarrow \left(f_s(o_t)=\frac{\sum_{t\in [0,T_m]}Id(q_t=s,o_t=e)}{\sum_{t\in[0,T_m]}Id(q_t=s)}, s\in S\right)](http://mathurl.com/ark5aup.png)
где Id(x) – индикаторная функция,
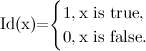
Для рассмотренного примера о детекторе лжи алгоритм неправильно классифицировал 413 из 10 000 состояний (~4%), что вовсе не плохо. Алгоритм Витерби способен с хорошей точностью детектировать моменты смены скрытых состояний, но только в случае, если распределения наблюдаемых характеристик точно известны. Если же известен только параметрический класс таких распределений, то существует способ выбора наиболее подходящих параметров, называемый алгоритм Баума-Велша.
Если интересно, требуйте продолжения…