
Spatial hashing это простая техника, которая используется в базах данных, физических и графических движках, симуляциях частиц и вообще везде, где нужно быстро что-то найти. Если в кратце, то суть в том, что мы разбиваем пространство с объектами на ячейки и складываем в них объекты. Затем вместо поиска по значению очень быстро ищем по хэшу.
Предположим, что у вас есть несколько объектов и вам нужно узнать нет ли между ними столкновений. Простейшим решением будет посчитать расстояние от каждого объекта до всех остальных объектов. Однако, при таком подходе количество необходимых вычислений растёт слишком быстро. Если на десятке объектов приходится делать сотню проверок, то на сотне объектов выходит уже десяток тысяч проверок. Это и есть печально известная квадратичная сложность алгоритма.
Здесь и далее используется псевдокод, подозрительно сильно похожий на C#, но это лишь иллюзия. Настоящий код приведён в конце статьи.
// В каждом объекте
foreach (var obj in objects)
{
if (Distance(this.position, obj.position) < t)
{
// Нашли одного соседа
}
}
Можно улучшить ситуацию, если разбить пространство с помощью сетки. Тогда каждый объект попадёт в какую-то ячейку сетки и будет довольно просто найти соседние ячейки, чтобы проверить их заполненность. Например, мы можем быть уверены, что два объекта не столкнулись, если их разделяет хотя бы одна ячейка.
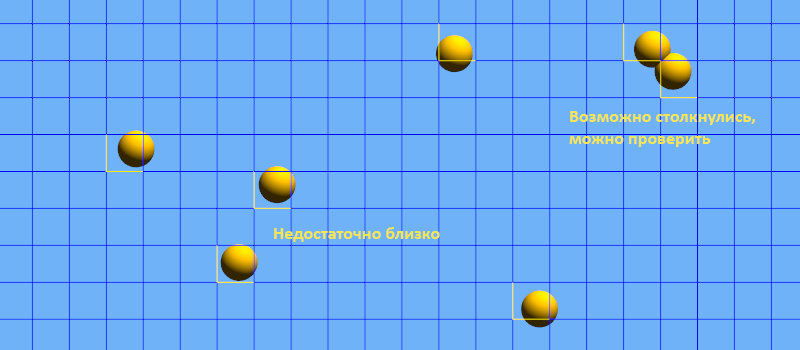
Сетка это уже хорошо, но появляется проблема с обновлением сетки. Постоянное просеивание координат по ячейкам может хорошо работать в двух измерениях, но в трёх уже начинает подтормаживать. Мы можем шагнуть дальше и свести многомерное пространство поиска к одномерному с помощью хеширования. Хеширование позволит нам быстрее наполнять ячейки и производить поиск по ним. Как же это работает?
Хэширование это процесс преобразования большого объёма данных к фиксированному, причем небольшое различие в исходных данных приводит в большому различию в фиксированном. По сути это сжатие с потерями. Мы можем назначить каждой ячейке свой идентификатор, и когда мы будем сжимать координаты объектов, проводя аналогию с картинками, понижать их разрешение, то автоматом получим координаты нужной ячейки. Заполнив таким образом все ячейки, мы затем можем легко достать объекты в окрестности любых координат. Мы просто хешируем координаты и получаем идентификатор ячейки с объектами.
Как может выглядеть хэш-функция для двухмерной сетки фиксированного размера? Например следующим образом:
hashId = (Math.Floor(position.x / сellSize)) + (Math.Floor(position.y / сellSize)) * width;
Мы делим координату икс на размер ячейки и отсекаем дробную часть, затем делаем то же самое с координатой игрек и умножаем на ширину сетки. Получается одномерный массив как на картинке снизу.

По сути мы имеем ту же самую сетку, что и раньше, но поиск происходит быстрее за счёт упрощения вычислений. Правда упрощаются они за счёт появления коллизий, когда хэш координат очень далёкого объекта может совпасть с хэшем координат близкого. Поэтому важен выбор хэш-функции с хорошим распределением и приемлемой частотой коллизий. Подробнее читайте в Википедии. Я же лучше покажу как можно на практике реализовать трёхмерный пространственный хэш.
Добавлю немного про хэши
Что быстрее посчитать 2 * 3,14 или 2 * 3,1415926535897932384626433832795028841971…? Разумеется первое. Мы получим менее точный результат, но кого это волнует? Точно так же и с хэшами. Мы упрощаем вычисления, теряем точность, но с большой вероятностью всё равно получаем результат, который нас устроит. В этом фишка хэшей и источник их силы.
Начнём с самого главного — хэш-функции для трёхмерных координат. В очень насыщенной статье на сайте Nvidia предлагают следующий вариант:
GLuint hash = ((GLuint)(pos.x / CELLSIZE) << XSHIFT) | ((GLuint)(pos.y / CELLSIZE) << YSHIFT) | ((GLuint)(pos.z / CELLSIZE) << ZSHIFT);
Берём координату по каждой оси, делим на размер ячейки, применяем побитовый сдвиг и OR'им результаты между собой. Авторы статьи не уточняют какой величины должен быть сдвиг, к тому же битовая математика не совсем «для самых маленьких». Есть функция немного проще, описанная в этой публикации. Если транслировать её в код, то получается что-то в этом роде:
hash = (Floor(pos.x / cellSize) * 73856093) ^ (Floor(pos.y / cellSize) * 19349663) ^ (Floor(pos.z / cellSize) * 83492791);
Находим координаты ячейки по каждой оси, умножаем на большое простое число и XOR'им. Честно говоря не намного проще, но по крайней мере без неизвестных сдвигов.
Для работы с пространственным хэшем удобно иметь два контейнера: один для хранения объектов в ячейках, другой для хранения номеров ячеек объектов. В качестве главных контейнеров быстрее всего работают хэштаблицы, они же словари, они же хэшмапы или как их ещё называют в вашем любимом языке. В одном из них мы получаем по ключу-хэшу хранимый объект, в другом по ключу-объекту номер ячейки. Вместе эти два контейнера позволяют быстро находить соседей и проверять заполненность ячеек.
private Dictionary<int, List<T>> dict;
private Dictionary<T, int> objects;
Как же выглядит работа с этими контейнерами? Мы вставляем объекты с помощью двух параметров: координат и собственно объекта.
public void Insert(Vector3 vector, T obj)
{
var key = Key(vector);
if (dict.ContainsKey(key))
{
dict[key].Add(obj);
}
else
{
dict[key] = new List<T> { obj };
}
objects[obj] = key;
}
Хэшируем координаты, проверяем наличие ключа в словаре, запихиваем по ключу объект и по объекту ключ. Когда же нам нужно обновить координаты, мы удаляем объект из старой ячейки и вставляем в новый.
public void UpdatePosition(Vector3 vector, T obj)
{
if (objects.ContainsKey(obj))
{
dict[objects[obj]].Remove(obj);
}
Insert(vector, obj);
}
Если за раз объектов обновляется слишком много, то проще очистить все словари и каждый раз заново наполнять.
public void Clear()
{
var keys = dict.Keys.ToArray();
for (var i = 0; i < keys.Length; i++)
dict[keys[i]].Clear();
objects.Clear();
}
Вот и всё, полный код класса представлен ниже. В нём используется Vector3 из движка Unity, но код легко может быть адаптирован для XNA или другого фреймворка. В функции хэша используется некое «быстрое округление», за его работу не ручаюсь.
SpatialHash.cs
using System.Linq;
using UnityEngine;
using System.Collections.Generic;
public class SpatialHash<T>
{
private Dictionary<int, List<T>> dict;
private Dictionary<T, int> objects;
private int cellSize;
public SpatialHash(int cellSize)
{
this.cellSize = cellSize;
dict = new Dictionary<int, List<T>>();
objects = new Dictionary<T, int>();
}
public void Insert(Vector3 vector, T obj)
{
var key = Key(vector);
if (dict.ContainsKey(key))
{
dict[key].Add(obj);
}
else
{
dict[key] = new List<T> { obj };
}
objects[obj] = key;
}
public void UpdatePosition(Vector3 vector, T obj)
{
if (objects.ContainsKey(obj))
{
dict[objects[obj]].Remove(obj);
}
Insert(vector, obj);
}
public List<T> QueryPosition(Vector3 vector)
{
var key = Key(vector);
return dict.ContainsKey(key) ? dict[key] : new List<T>();
}
public bool ContainsKey(Vector3 vector)
{
return dict.ContainsKey(Key(vector));
}
public void Clear()
{
var keys = dict.Keys.ToArray();
for (var i = 0; i < keys.Length; i++)
dict[keys[i]].Clear();
objects.Clear();
}
public void Reset()
{
dict.Clear();
objects.Clear();
}
private const int BIG_ENOUGH_INT = 16 * 1024;
private const double BIG_ENOUGH_FLOOR = BIG_ENOUGH_INT + 0.0000;
private static int FastFloor(float f)
{
return (int)(f + BIG_ENOUGH_FLOOR) - BIG_ENOUGH_INT;
}
private int Key(Vector3 v)
{
return ((FastFloor(v.x / cellSize) * 73856093) ^
(FastFloor(v.y / cellSize) * 19349663) ^
(FastFloor(v.z / cellSize) * 83492791));
}
}
В интерактивной демонстрации по этой ссылке вы можете посмотреть как распределяется хэш-пространство. Координаты жёлтого шарика хэшируются по таймеру, после чего он перемещается в случайную точку внутри сферы. Жёлтые кубики обозначают координаты, которые попадут в ту же самую ячейку. Синим цветом обозначены уже созданные ключи, чтобы вы могли посмотреть на процесс заполнения памяти. Мышкой можно вращать.
Исходники на GitHub | Онлайн версия для обладателей Unity Web Player
Интересные ссылки по теме
http://www.cs.ucf.edu/~jmesit/publications/scsc%202005.pdf
http://www.beosil.com/download/CollisionDetectionHashing_VMV03.pdf
http://http.developer.nvidia.com/GPUGems3/gpugems3_ch32.html