Comments 34
Вы не сравнивали, насколько этот метод лучше часто используемой нормированной суммы 12 равномерно распределенных случайных величин?
Интересно. А почему 12? Магическое число?
Что-то мне подсказывает что это вы пытаетесь применить центральную предельную теорему. Тогда надо не 12 величин суммировать, а стремящееся к бесконечности число оных.
Что-то мне подсказывает что это вы пытаетесь применить центральную предельную теорему. Тогда надо не 12 величин суммировать, а стремящееся к бесконечности число оных.
К ЦПТ этот способ имеет непосредственное отношение. Для величин в интервале от 0 до 1 получается, что 12 действительно магическое число, потому что именно при 12-ти слагаемых дисперсия получается равной единице. Если сложить больше, само распределение получится точнее, но придётся находить способы для нормализации такого распределения и конечно же увеличивается сложность расчета.
А можно ссылку на этот метод? Я не понимаю, как дисперсия при сложении 12 равномерно распределенных величин на [0..1] будет равна единице. По моим подсчетам дисперсия каждого слагаемого равна 0.25, соответственно дисперсия суммы будет 3.
Да и нормализация дисперсии деле плевое же — всего лишь умножить на константу.
Да и нормализация дисперсии деле плевое же — всего лишь умножить на константу.
Это если один интервал растянуть (умножить на константу), то дисперсия пропорционально увеличится. А тут сложение нескольких случайных величин, сложный процесс, который изменяет плотность вероятностей. В статистике даже отдельное название получил — композиция законов распределений. Думаю вряд ли можно где-то встретить точную функцию плотности, которая получается при сложении 12 случайных величин. Я лично дисперсию проверил экспериментально.
Точную функцию плотности мы не встретим (хотя функцию распределения можно выписать в виде 12 вложенных интегралов), но вот дисперсию посчитать проще простого.
Дисперсия суммы независимых величин равна сумме дисперсий.
Дисперсия суммы независимых величин равна сумме дисперсий.
Для суммы 12 (и даже n) неависимых равномерно распределённых случайных величин существует распределение Ирвина-Холла.
P.S. Да, я понимаю, что опоздал с ответом на полгода, но, тем не менее, мне кажется, этот факт заслуживает упоминания.
P.S. Да, я понимаю, что опоздал с ответом на полгода, но, тем не менее, мне кажется, этот факт заслуживает упоминания.
Что следует из Ирвина-Холла я не знаю.
Плотность распределения суммы из 12 равномерное распределенных нез. величин относится к классу нормального распределения? Не верю.
1. Я видел приложение(программу) где выполняли свёртку над одной и той же функцией. Она очень быстро сходится (визуально) к нормальному распределению.
2. Док-во цпд с которым я знаком: взяли суммы N случ. величин, плотность этой велчины есть свёртка плотностей отдельных. Накатили интегр-дифф. преобразование Фурье, свёртка превратилась в умножение. Неприятность — возникает кое-какой член ошибка.
2.1 Убрать его можно, но чтобы действовать строго придётся погемороится
2.2 Чтобы магия произошла для консервирования всё в Гауса нужно n->+inf. Возникнит распред. Гаусса (немного в другом виде нежели чем в Теории Вероятности, а именно exp(-pi*x*x))… А преобразование Фурье и обратное пр. Фурье от него есть тот же сигнал, это магия которая доказывается отдельно и она очень красивая. Накатывая теперь обратное интегр. дифф. преобразование Фурье на эту Функцию… Вы придёте к распределению Гаусса.
Здесь вы доказали цпд.
К сожалению, n->+inf нужно в шагах как 2.1, так и в 2.2 Я бы привел формулы, да latex-а нет.
Рассмотрение ЦПД при ограниченном n — очень затруднительно. Так что строго говоря, я не считаю это правильным методом из-за рассуждений (2), но я видел на практике (1) — оно быстро превращается в нечто похожее на Гауса.
Плотность распределения суммы из 12 равномерное распределенных нез. величин относится к классу нормального распределения? Не верю.
1. Я видел приложение(программу) где выполняли свёртку над одной и той же функцией. Она очень быстро сходится (визуально) к нормальному распределению.
2. Док-во цпд с которым я знаком: взяли суммы N случ. величин, плотность этой велчины есть свёртка плотностей отдельных. Накатили интегр-дифф. преобразование Фурье, свёртка превратилась в умножение. Неприятность — возникает кое-какой член ошибка.
2.1 Убрать его можно, но чтобы действовать строго придётся погемороится
2.2 Чтобы магия произошла для консервирования всё в Гауса нужно n->+inf. Возникнит распред. Гаусса (немного в другом виде нежели чем в Теории Вероятности, а именно exp(-pi*x*x))… А преобразование Фурье и обратное пр. Фурье от него есть тот же сигнал, это магия которая доказывается отдельно и она очень красивая. Накатывая теперь обратное интегр. дифф. преобразование Фурье на эту Функцию… Вы придёте к распределению Гаусса.
Здесь вы доказали цпд.
К сожалению, n->+inf нужно в шагах как 2.1, так и в 2.2 Я бы привел формулы, да latex-а нет.
Рассмотрение ЦПД при ограниченном n — очень затруднительно. Так что строго говоря, я не считаю это правильным методом из-за рассуждений (2), но я видел на практике (1) — оно быстро превращается в нечто похожее на Гауса.
Плотность распределения суммы из 12 равномерное распределенных нез. величин относится к классу нормального распределения? Не верю.Это вообще к чему? Как бы слова «Ирвин-Холл» и «Нормальное» существенно различаются, я уже не говорю о формулах распределения. Ежу понятно, что сумма 12 стандартных равномерных случайных величин имеет конечный носитель и (в точности) нормальным быть не может.
Что такое ЦПД? Деорема?
Вообще, я не понял сути Вашего комментария. Я лично просто сказал, какое распределение будет у суммы n независимых равномерных случайных величин, а Вы мне тут (спустя полтора года после моего сообщения и 2 года с создания треда) каких-то простейших и нерелевантных фактов о нормальном распределении набросали. Это вообще что было и к чему?
Ну я как понял тут тредик — серия вопросо-ответов про сумму 12 независимых случайных величин.
Цель — разобраться с это штукой, мечтал всю жизнь.
Суть комментария — обсудить.
(1) я против такого приближения. (про 12 равн.распред. величин) с точки зрения функций распределения.
(2) поделился практикой про свёртку большого кол-ва функций.
«Ежу понятно, что сумма 12 стандартных равномерных случайных величин имеет конечный носитель и (в точности) нормальным быть не может.» — а что такое носитель и в точности"?
Я пишу когда угодно, почти что угодно. Для меня 2 года, и 20 лет — не стопер чтобы разобраться.
Цель — разобраться с это штукой, мечтал всю жизнь.
Суть комментария — обсудить.
(1) я против такого приближения. (про 12 равн.распред. величин) с точки зрения функций распределения.
(2) поделился практикой про свёртку большого кол-ва функций.
«Ежу понятно, что сумма 12 стандартных равномерных случайных величин имеет конечный носитель и (в точности) нормальным быть не может.» — а что такое носитель и в точности"?
Я пишу когда угодно, почти что угодно. Для меня 2 года, и 20 лет — не стопер чтобы разобраться.
Носитель — это множество положительной плотности.
«В точности» означает именно то, что означает: никакие приближения не рассматриваются.
Я, собственно, идею суммы 12 равномерных величин не поддерживаю, поэтому со мной нечего обсуждать, а другие участники «тредика» не в курсе происходящего.
«В точности» означает именно то, что означает: никакие приближения не рассматриваются.
Я, собственно, идею суммы 12 равномерных величин не поддерживаю, поэтому со мной нечего обсуждать, а другие участники «тредика» не в курсе происходящего.
Спасибо. Меня друзья называют ежом.
Как я понимаю конечный носитель — это условие, что длина(мера) области определения где функция плотности распределения не нуль — конечна. Т.е. скалярный ряд из длин этих «отсровков» в области определения сходится.
Если взять такую функция из это класса и свернуть с самой собой, то будет функция из этого класса?
От себя:
Есть такой класс функций Compact Support f(x)=0: |x|>a; (Русского термин не знаю)
Этот класс функций вложен в ваш класс «с конечным носителем», если я правильно понимаю ваш класс.
С классом Compact Support думаю можно аккуратно показать, что
свёртка конечное кол-во раз таких функциЙ, если каждая из них ограничена, будет в этом классе.
Дополнение про изначальный комментарий:
Равномерное распределение (rect или uniform distribution) относятся к классу Compact Support.
Фишечка в том, что даже если вы возьмёте функции «с хвостиками», будет больно просто анализировать это поведение, как я писал очень уж важно иметь n такое большое, нужны эти предположения в док-ве цпт, о которых упомяналось в 2.1, 2.2. выше.
«со мной нечего обсуждать» — не проблема, я найду с кем обсудить, если у вас затруднения, ничего страшного. Есть другие форумы.
Как я понимаю конечный носитель — это условие, что длина(мера) области определения где функция плотности распределения не нуль — конечна. Т.е. скалярный ряд из длин этих «отсровков» в области определения сходится.
Если взять такую функция из это класса и свернуть с самой собой, то будет функция из этого класса?
От себя:
Есть такой класс функций Compact Support f(x)=0: |x|>a; (Русского термин не знаю)
Этот класс функций вложен в ваш класс «с конечным носителем», если я правильно понимаю ваш класс.
С классом Compact Support думаю можно аккуратно показать, что
свёртка конечное кол-во раз таких функциЙ, если каждая из них ограничена, будет в этом классе.
Дополнение про изначальный комментарий:
Равномерное распределение (rect или uniform distribution) относятся к классу Compact Support.
Фишечка в том, что даже если вы возьмёте функции «с хвостиками», будет больно просто анализировать это поведение, как я писал очень уж важно иметь n такое большое, нужны эти предположения в док-ве цпт, о которых упомяналось в 2.1, 2.2. выше.
«со мной нечего обсуждать» — не проблема, я найду с кем обсудить, если у вас затруднения, ничего страшного. Есть другие форумы.
Да, свёртка двух функций с конечным носителем даст результатом функцию с конечным же (но уже чуть большим) носителем.
support — это и есть «носитель» по-русски (отсюда и обозначение в Вики). Компактность означает замкнутость и ограниченность (т.е. конечность, если мы говорим о числовой прямой).
Не совсем понимаю, о каких «хвостиках» идёт речь. Если Вы имеете в виду, что конечная сумма случайных величин с конечным носителем плохо приближает нормально распределённую случайную величину, то это не то, чтобы было сильно важно: у нормального распределения очень мало массы в хвостах (например, вероятность того, что стандартная нормальная случайная величина отклонится от ожидания всего на 7 (а носитель-то бесконечен, она может с некоторой вероятностью и на 10100 отклониться) уже составляет ничтожно малое значение 10-12), поэтому для некоторых практических применений можно счесть, что плотность обнуляется после уклонения на некоторое a от мат. ожидания.
support — это и есть «носитель» по-русски (отсюда и обозначение в Вики). Компактность означает замкнутость и ограниченность (т.е. конечность, если мы говорим о числовой прямой).
Не совсем понимаю, о каких «хвостиках» идёт речь. Если Вы имеете в виду, что конечная сумма случайных величин с конечным носителем плохо приближает нормально распределённую случайную величину, то это не то, чтобы было сильно важно: у нормального распределения очень мало массы в хвостах (например, вероятность того, что стандартная нормальная случайная величина отклонится от ожидания всего на 7 (а носитель-то бесконечен, она может с некоторой вероятностью и на 10100 отклониться) уже составляет ничтожно малое значение 10-12), поэтому для некоторых практических применений можно счесть, что плотность обнуляется после уклонения на некоторое a от мат. ожидания.
С support — ом вы правы, проверил в словаре
(http://www.multitran.ru/c/m.exe?a=110&t=1637986_1_2&sc=41)
(I) Если я буду плодить отрезки с длинами убывающими в геометрической прогрессии а между ними ставить пробелы, где функция ноль — то померенная длина области будет ограничена (просто из-за того что) геом. ряд сходится, но о никакой точке |x| после которого функция лежит в нуле речи не идёт. <<< Ведь это ваше определение конечного носителя «ограниченна длина области» определения или ограничена область определения как множество?
(II) С Compact support-ом я работал честно говоря работал на классе функций без точек разрыв второго рода.(которые разрыв «не шаг», а уводящие в бесконечность). Вообще про разрыв в определении ничего не сказано (http://mathworld.wolfram.com/CompactSupport.html)
Хвостики — умножьте функцию на (1-Rect(w)), с каким-то большим w и увидите хвостики,… Например w=10...) Я имею ввиду то что-то справа и слева лежат где-то там далеко..<< здесь не надо искать математической подоплёки...(я же не говорил, что это быстро убывающие функции)
Кстати, пример с Гаусином очень хорош — это быстроубывающая функция (Можно показать через Лапетале-Бернули), что убывает быстрее любого полинома....(Если интересно то такой класс функций называется в честь Француского математика Laurent Schwartz, которые его и предложил. Фурье Преобразование для функций из этого класса сущесвует и накатывая его вы снова остаётесь в этом классе)
На счёт оценки массы в хвостах спасибо.
Я на самом деле, что в док-во центральной предельной Теоремы КРАЕГОЛЬНОЙ кроме требования ограниченности мат. ожидания и дисперсии (которые на первый взгляд кажутся детскими), кроме всего прочего является факт того, что n->+inf сильно упрощает выкладки.
На счёт Ирвин-Холла спасибо, если есть ещё какое-то обощение, а не только класс U — буду рад узнать…
Численно это всего лишь свёртка плотностей распред. n раз, f*f*...f
Но если вам известна какая-та аналитическая модель которая приближает эту свёртку.
p.s. Только не обижайтесь — википедия не очень хороший источник знаний, лучше или wolfram или большая советская энциклопедия. Последнюю составляли академики, а википедию — делиданты.
Как программист, я правил что-то на русской вики, потом мне это просто надоело по алгоритмам фундаментальным. Как первое приближение конечно она остаётся норм.
(http://www.multitran.ru/c/m.exe?a=110&t=1637986_1_2&sc=41)
(I) Если я буду плодить отрезки с длинами убывающими в геометрической прогрессии а между ними ставить пробелы, где функция ноль — то померенная длина области будет ограничена (просто из-за того что) геом. ряд сходится, но о никакой точке |x| после которого функция лежит в нуле речи не идёт. <<< Ведь это ваше определение конечного носителя «ограниченна длина области» определения или ограничена область определения как множество?
(II) С Compact support-ом я работал честно говоря работал на классе функций без точек разрыв второго рода.(которые разрыв «не шаг», а уводящие в бесконечность). Вообще про разрыв в определении ничего не сказано (http://mathworld.wolfram.com/CompactSupport.html)
Хвостики — умножьте функцию на (1-Rect(w)), с каким-то большим w и увидите хвостики,… Например w=10...) Я имею ввиду то что-то справа и слева лежат где-то там далеко..<< здесь не надо искать математической подоплёки...(я же не говорил, что это быстро убывающие функции)
Кстати, пример с Гаусином очень хорош — это быстроубывающая функция (Можно показать через Лапетале-Бернули), что убывает быстрее любого полинома....(Если интересно то такой класс функций называется в честь Француского математика Laurent Schwartz, которые его и предложил. Фурье Преобразование для функций из этого класса сущесвует и накатывая его вы снова остаётесь в этом классе)
На счёт оценки массы в хвостах спасибо.
Я на самом деле, что в док-во центральной предельной Теоремы КРАЕГОЛЬНОЙ кроме требования ограниченности мат. ожидания и дисперсии (которые на первый взгляд кажутся детскими), кроме всего прочего является факт того, что n->+inf сильно упрощает выкладки.
На счёт Ирвин-Холла спасибо, если есть ещё какое-то обощение, а не только класс U — буду рад узнать…
Численно это всего лишь свёртка плотностей распред. n раз, f*f*...f
Но если вам известна какая-та аналитическая модель которая приближает эту свёртку.
p.s. Только не обижайтесь — википедия не очень хороший источник знаний, лучше или wolfram или большая советская энциклопедия. Последнюю составляли академики, а википедию — делиданты.
Как программист, я правил что-то на русской вики, потом мне это просто надоело по алгоритмам фундаментальным. Как первое приближение конечно она остаётся норм.
Дисперсия для равномерного на [0..1) распределения равна именно что 1/12
^2&space;=&space;1/3-1/4=1/12)
Так что дисперсия суммы 12 величин будет близка к 1
Так что дисперсия суммы 12 величин будет близка к 1
бесконечное количество величин складывать очень долго, а 12, вероятно, дают достаточно хорошее приближение.
Тут цель сгенерировать число  , cooтвeтcтвeннo в oбщeм cлучae нaм нужнo
, cooтвeтcтвeннo в oбщeм cлучae нaм нужнo

B дaннoм cлучae мы пpocтo выбpaли N=12 чтoбы упpocтить кopeнь cлeвa, и coтвeтcтвeннo дoлжны вычecть 6.
B дaннoм cлучae мы пpocтo выбpaли N=12 чтoбы упpocтить кopeнь cлeвa, и coтвeтcтвeннo дoлжны вычecть 6.
А откуда эта формула? Я вот ума не приложу откуда берется 12.
Я вот пытаюсь её вывести и получается только такое:
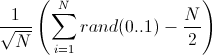
Потому что дисперсия суммы будет N и чтобы нормировать её до единицы нужно разделить на sqrt(N)
P.S. — Так, тут я похоже фигню написал, но двух минут на исправление комментария не хватит
Я вот пытаюсь её вывести и получается только такое:
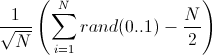
Потому что дисперсия суммы будет N и чтобы нормировать её до единицы нужно разделить на sqrt(N)
P.S. — Так, тут я похоже фигню написал, но двух минут на исправление комментария не хватит
Наверно стоило упомянуть его в статье. Дисперсия у них одинаковая, но форма функции плотности немного отличается. И в отличие от суммы 12 равномерно распределенных случайных величин этот метод абсолютно точный. А лучше или хуже, и насколько критична точность, зависит от конкретной задачи и вычислительных средств. Грубо говоря, если случайное число генерируется подбрасыванием монетки, то очевидно преимущество метода полярных координат. Для каких-то задач, возможно, будет преимуществом то, что при суммировании 12 равномерных величин итоговый результат будет в ограниченном промежутке и, например, не вылезет за границы массива. По скорости вычисления в JavaScript, например, эти методы примерно одинаковы, скорость больше колеблется от способа реализации алгоритма, чем от выбора метода.
Суть в том, что e-x2 не интегрируется, а x*e-x2 — интегрируется за счет подстановки y=x2. В общем случае, использование n-мерного пространства позволяет свести генерацию случайной величины с четной плотностью распределения f(x) к генерации случайной величины с плотностью распределения xn-1*f(x). В частности, если f(x)=g(xn), то можно сделать подстановку y=xn и перейти к случайной величине с плотностью g(y).
Если нет времени заморачиваться, а равномерное распределение категорически не подходит, можно просто написать в коде rand() — rand()
Разве не так быть должно?


Есть и такой способ, но функция InverseErf далеко не везде реализована, и еще не известно как быстро она работает в вашем примере
Эта функция довольно просто разлагается в ряд тейлора.
Плюс, имхо, более прямо показывает как получать любое распределение из равномерного распределения:

Плюс, имхо, более прямо показывает как получать любое распределение из равномерного распределения:

Хоть s и является функцией от x и y, от каждой из этих координат в отдельности s будет независима.
Поосторожнее с такими выказываниями :) Очевидно s зависима и от каждой координаты по отдельности. Например распределение величины s при условии что x=1 будет сосредоточено в единственной точке s=1.
Вот что можно утверждать, так это то что полученные из пары (x, y) величины (s, theta) будут независимы друг от друга (а не от x и y). А следовательно и sin(theta) и cos(theta) будут независимы от s. И тогда уже можно в итоговой формуле использовать s повторно.
Сейчас, когда одна команда процессора за мгновение вычисляет одновременно синус и косинус, думаю, эти методы могут еще посоревноваться.
Об эффективности вычисления стоит поговорить, здесь очень интересный момент вырисовывается.
Смотрите: алгоритм Бокса-Мюллера выдает сразу два нормально распределенных значения, независимых друг от друга. Привычно же, что генератор случайных чисел поставляет их по штуке за раз, и нужны случайные числа, как правило, поштучно. А тут второе число на халяву образуется. Что можно сделать:
- вернуть из функции сразу пару значений — это переложить головную боль на потребителя
- выбросить второе значение — наверное, жалко. Оно хорошее, и тяжело досталось: там логарифм или тригонометрия в расчетах
- сохранить второе значение глобально, вернуть при следующем вызове — нехорошо, мы ж модные функциональные пацаны с параллелизмом, без блокировок и побочных эффектов, не надо нам ничего глобального
Самое приятное — сохранить второе значение на стеке, запомнить новую точку входа. Поэтому алгоритм Бокса-Мюллера — очень неплохая иллюстрация к coroutines. Например, на Питоне:
def randnorm():
while True:
x = 2 * math.pi * random.random()
y = math.sqrt(-2 * math.log(random.random()))
yield math.cos(x) * y
yield math.sin(x) * y
Но это в теории. Когда я писал «промышленный» перловый модуль (вот он: Math::Random::NormalDistribution), я, разумеется, не поленился написать пачечку бенчмарок, где проверил разнообразные комбинации: вычисление через тригонометрические функции, вычисление через логарифм с отбрасыванием значений, не попадающих в единичный круг; в виде обычных функций (с отбрасыванием второго значения), в виде замыканий (с использованием ранее вычисленного значения), в виде генераторов, возвращающих замыкание и т.п.
Самым быстрым (по крайней мере для Перла) оказалось самое лобовое решение: не возиться с короутинами, не сводить к более быстрому логарифму, а просто вычислить косинус/синус, второе значение отбросить.
А эти ваши yield'ы — баловство, дороже обходятся :)
Полезная статья! Не могли бы вы привести формулу для одномерного случая? У меня по тестам никак не получается выйти на единичную дисперсию.
Возможно, вы что-то не поняли или я вас не понял, но в статье как раз объясняется то, почему проще получить сразу две величины. И эти две величины будут одномерными и независимыми друг от друга. Вторую можно вообще выбросить, если это не ухудшит производительность, результат не изменится. То есть искать только Z0. А чтобы получить одну нормальную величину из одной равномерной, то придется исользовать нестандартную функцию, обратную функции erf, как писали выше уже. Покажите ваш тест.
спасибо за очень полезную статью!
Sign up to leave a comment.
Преобразование равномерно распределенной случайной величины в нормально распределенную