
Хей народ, пристегните ремни и держитесь покрепче, ибо наступил действительно волнительный момент: вам предстоит разобраться в тонкостях чрезвычайно интересных временных функций CSS!
Окей, ваша кровь, конечно, вряд ли закипела от предмета данной статьи, но шутки в сторону: временные функции — своего рода скрытая жемчужина, когда дело касается CSS, и, вполне вероятно, вы удивитесь тому, сколько всего интересного с помощью них можно сделать.
Прежде всего, мы должны четко понимать, когда применяются временные функции в CSS. Так вот, данный функционал предназначен для работы с CSS анимацией: переходами (transitions) и покадровой анимацией (keyframes).
О временной функции в CSS
Данное свойство — одно из самых неочевидных в CSS анимации, в то время как большинство свойств из этой категории вполне самопонятны. Тем не менее, суть его в контроле и изменении скорости анимации: оно определяет точки ускорения и замедления за указанный период времени.
С помощью данного свойства можно достичь разного восприятия пользователем скорости анимации, в то время как её фактическая продолжительность остается неизменной. Так что если вы еще не решили убежать без оглядки, пойдемте дальше, ибо временные функции таят в себе гораздо больше всякого интересного, нежели следует из сухой спецификации.
Заметка: свойства
timing-function не существует. Называя это свойство, на самом деле я имею в виду transition-timing-function и animation-timing-function.Прежде чем пойти дальше, давайте познакомимся с синтаксисом и посмотрим, как он вписывается в весь процесс определения CSS анимации. Простоты ради, давайте используем CSS переход и пропишем все transition-свойства по отдельности:
div {
transition-property: background;
transition-duration: 1s;
transition-delay: .5s;
transition-timing-function: linear;
}
/* This could, of course, be shortened to: */
div {
transition: background 1s .5s linear;
}
Сокращенная запись перехода не имеет строгого порядка значений, но требует, чтобы значение
transition-delay находилось после значения transition-duration (не обязательно непосредственно после). Кроме того, значение transition-duration является единственным необходимым для определения функции. А поскольку значения по умолчанию у остальных параметров вполне приемлемы, для определения перехода вам редко понадобится нечто большее, чем:div {
transition: 1s;
}
/* То же, что: */
div {
transition: all 1s 0s ease;
}
Но это же скучно. Несмотря на то, что значений по умолчанию вполне достаточно для какого-нибудь обычного hover'а, когда вы работаете над чем-то более существенным, временные функции оказываются серьезным инструментом для тонкой настройки ваших анимаций!
Теперь, когда вы знаете, что делают временные функции, пришла пора узнать, как они это делают.
Заглянем под капот
Многие из вас наверняка не заостряли свое внимание на допустимых значениях свойства
timing-function. Так вот, их пять: ease (по умолчанию), ease-in, ease-out, ease-in-out и linear. При этом данные значения — всего лишь короткая запись определения кривой Безье.Э-э, что?!
Вы можете быть незнакомы с данным термином, однако я держу пари, что в действительности вам доводилось видеть кривую Безье. Черт побери, если вы использовали какой-либо графический пакет, то наверняка даже сами создавали её! Именно так, ибо когда вы используете инструмент Pen или Path для создания гладкой кривой, то, что у вас получается, — и есть кривая Безье! В нашем случае она — «волшебство» временной функции, описывающее тип ускорения на графике.

Данная кривая Безье соответствует значению ease (изображение принадлежит Smashing Magazine)
Если ваша реакция на впервые увиденную кривую Безье была подобна моей, у вас наверняка возник вопрос: как вообще такая кривая может быть построена по четырем точкам на графике?! Вряд ли смогу я вам объяснить это на словах, однако у меня есть фантастическая гифка, которая поможет мне в этом:
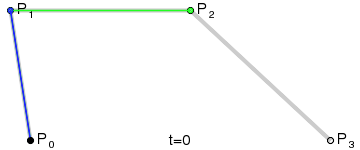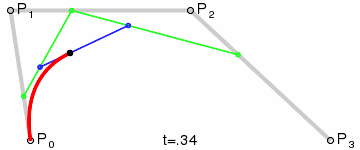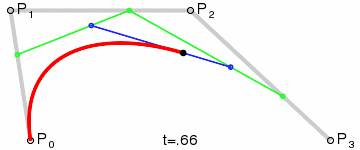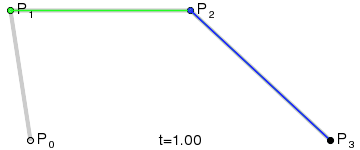
Рисование кривой Безье (изображение взято из Википедии)
Поскольку данная кривая строится по четырем точкам, мы называем ее кубической (cubic) кривой Безье, в отличие от квадратичной кривой (quadratic, по трем точкам) и кривой четвертого порядка (quartic, по пяти точкам).
Функция cubic-bezier()
А вот сейчас вам станет еще интереснее, ибо я скажу, что вы можете задавать кубическую кривую с помощью функции
cubic-bezier(), используя её вместо ключевых значений свойства timing-function. Полагаю, вам необходимо некоторое время, дабы сдержать волнение.С помощью функции
cubic-bezier() вы можете манипулировать кривой так, как вам заблагорассудится, задавая при этом абсолютно любые параметры ускорения вашей анимации! Так что давайте посмотрим, как эта функция работает и каким образом она позволяет создавать собственные кривые Безье.Во-первых, мы уже знаем, что кубическая кривая строится по четырем точкам: 0, 1, 2, 3. Во-вторых, важно помнить, что первая и последняя точки (0 и 3) уже определены на графике, где точка 0 всегда имеет значение
0;0 (снизу слева), а точка 3 — 1;1 (сверху справа).Данное условие оставляет нам всего две точки, которые необходимо разместить на графике, и сделать это можно с помощью функции
cubic-bezier()! Она принимает четыре аргумента: первые два — координаты x, y первой точки; вторые два — координаты x, y второй точки.transition-timing-function: cubic-bezier(x1, y1, x2, y2);
Чтобы вы освоили синтаксис и то, как эта функция создает кривую, а также её физическое влияние на анимацию, я покажу вам пять ключевых значений свойства
timing-function, их эквивалент для cubic-beizer() и результирующий эффект анимации.EASE-IN-OUT
Давайте начнем с данного ключевого значения, поскольку и логику построения кривой, и переложение её на анимацию сейчас, вероятно, проще всего понять.
/* Эквивалент ключевому значению ease-in-out */
transition-timing-function: cubic-bezier(.42, 0, .58, 1);
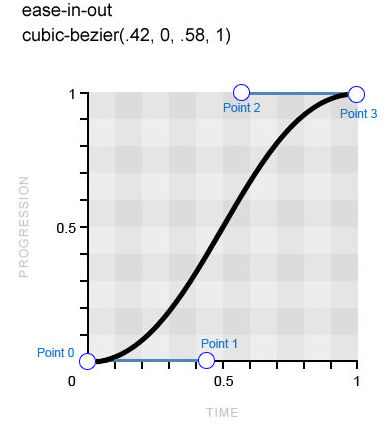
Совершенно симметричная кривая Безье, что означает, что ускорение и замедление анимации будет производиться с одинаковой скоростью (изображение принадлежит Smashing Magazine)
Точка 1 расположена на
0,42 по оси x и на 0 по оси y, в то время как точка 2 — на 0,58 и 1 соответственно. Результат — совершенно симметричная кривая Безье: ускорение и замедление анимации будет происходить с одинаковой скоростью. Отсюда и название ключевого слова.Посмотрите на демонстрацию и вы увидите физический эффект значения
ease-in-out, сравните его с другими значениями.
Исходная анимация на Codepen
EASE
Данное ключевое значение является значением по умолчанию свойства
timing-function. На самом деле, оно очень похоже на предыдущее, хотя ускорение анимации происходит быстрее, а замедление — более постепенно./* Эквивалент ключевому значению ease */
transition-timing-function: cubic-bezier(.25, .1, .25, 1);
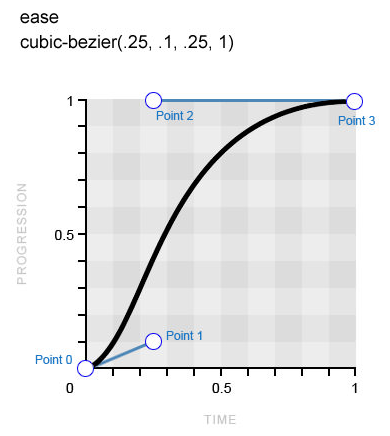
Кривая
ease имеет крутое начало и много более плавное продолжение (изображение принадлежит Smashing Magazine)Обратите внимание на более четкий наклон кривой в начале, в то время как конец её более вытянутый, — это напрямую оказывает физический эффект временной функции на анимацию. Когда изучите все примеры, не забудьте вернуться к демонстрации в начале, чтобы сравнить эффекты между собой.
EASE-IN И EASE-OUT
Как не сложно догадаться, данные ключевые значения имеют противоположный смысл.
ease-in плавно ускоряет анимацию развивая максимальную скорость к её завершению, в то время как ease-out плавно снижает изначально максимальную скорость перед завершением анимации. Следуя логике, ключевое значение ease-in-out, которое мы рассмотрели ранее, — отличная комбинация этих двух кривых Безье./* Эквивалент ease-in */
transition-timing-function: cubic-bezier(.42, 0, 1, 1);
/* Эквивалент ease-out */
transition-timing-function: cubic-bezier(0, 0, .58, 1);
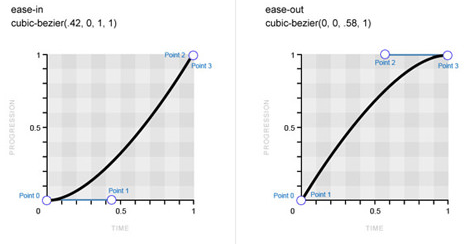
Кривые Безье:
ease-in слева, ease-out справа (изображение пренадлежит Smashing Magazine)LINEAR
Последнее ключевое значение, которое вообще-то к кривым не относится. Исходя из названия, значение
linear свойства timing-function устанавливает одинаковую скорость в течение всей анимации, что означает, что вместо кривой Безье мы получим прямую линию. То есть в данном случае не имеется какой-либо модели ускорения для изображения на графике./* Эквивалент linear */
transition-timing-function: cubic-bezier(0, 0, 1, 1);

Значение
linear подразумевает одинаковую скорость на протяжении всей анимации (изображение принадлежит Smashing Magazine)Если вы вновь посмотрите демо в начале, то наверняка заметите, что несмотря на одинаковую общую продолжительность, некоторые из анимаций кажутся медленнее остальных. Почему же так происходит? Ну, например, у
ease-in-out начало и завершение анимации проходит с оттяжкой. Поэтому, чтобы уложиться в заданную продолжительность, в основной части скорость анимации существенно выше. В виду такого поведения мы воспринимаем её и короче, и быстрее, тогда как, например, линейная анимация кажется нам длинной и растянутой.Возможно, к этому моменту у вас уже возникло ощущение, что данная статья слишком уж медленно подходит к своей истинной сути, так что давайте прямо сейчас перейдем к рассмотрению функции
cubic-bezier() и созданию собственных временных функций с её помощью.Создание собственных моделей ускорения с помощью функции cubic-bezier()
Теперь, когда мы узнали ключевые значения свойства
timing-function и соответствующие им кривые Безье, а также понаблюдали их воздействие на анимацию, давайте научимся создавать собственные модели ускорения с помощью манипуляций кривой.К настоящему моменту предполагается, что вы уже умеете располагать точки 1 и 2 на графике с помощью функции
cubic-bezier(), а также ясно представлять, каким образом это влияет на анимацию. Хотя, если вы делаете это «в слепую», не удивительно, что данное занятие может очень быстро надоесть.К счастью, существуют на Земле такие люди, как Лиа Веру (Lea Verou), которые, вероятно, не успокоятся пока кодинг на CSS не станет еще легче! Ли разработала приложение «Кубический Безье» для создания собственных кривых Безье и сравнения их со стандартными. Так что вместо того, чтобы гонять туда-сюда циферки в
cubic-bezier(), зайдите на Cubic Bézier, поиграйтесь с кривой да посмотрите на результат. Это куда круче!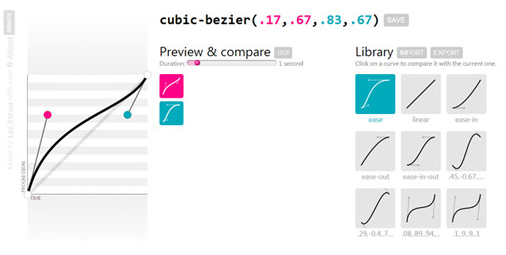
Скришнот страницы сайта Cubic Bézier (изображение принадлежит Smashing Magazine)
На начальном этапе стандартные кривые временной функции — то, что надо, только различия между ними не так очевидны. Зато как только вы начнете создавать собственные кривые Безье, вы почувствуете, насколько мощным может быть их влияние на результирующую анимацию.
Просто взгляните на следующие примеры и обратите внимание на существенное различие между анимациями при их одинаковой общей продолжительности.

Исходная анимация на Codepen
Ну, а теперь давайте разберемся с самым первым из приведенных выше примеров и попытаемся понять, каким образом получился столь отличный от остальных эффект.
/* Значения cubic-bezier() для первого примера из демо */
transition-timing-function: cubic-bezier(.1, .9, .9, .1);
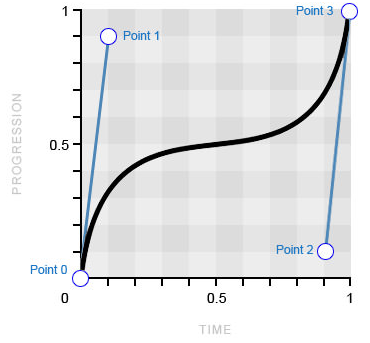
Пример нестандартной кривой Безье (изображение принадлежит Smashing Magazine)
Основное отличие данной временной функции от значений по умолчанию состоит в резком отклонении кривой от шкалы «прогрессии» (по оси y). Это обуславливает быстрый старт и завершение анимации, но затяжную паузу в середине (в том месте, где кривая выравнивается). Данная модель резко контрастирует с той, к которой мы привыкли с обычными временными функциями, которые используют противоположный подход, замедляя анимацию в начале и конце, а не по середине.
А теперь проявим изобретательность
Да-да: кривые Безье становятся еще более захватывающими! И кто бы мог подумать? Тем временем, границы воображения расширяются с открытием того, что лишь шкала времени (по оси x) ограничена на графике промежутком от нуля до единицы, в то время как шкала прогрессии (по оси y) может выходить за его рамки как снизу, так и сверху.
Шкала прогрессии — это именно то, о чем вы подумали: нижний конец (0) являет собой начало анимации, а верхний (1) — завершение. Как правило, кубическая кривая Безье всегда следует снизу вверх по данной шкале с разной интенсивностью, пока не достигнет конечной точки анимации. Тем не менее, возможность располагать точки 1 и 2 вне промежутка 0-1 позволяет кривой выходить за его пределы, что вызывает движение в обратном направлении! Как обычно, лучший способ понять это — посмотреть:
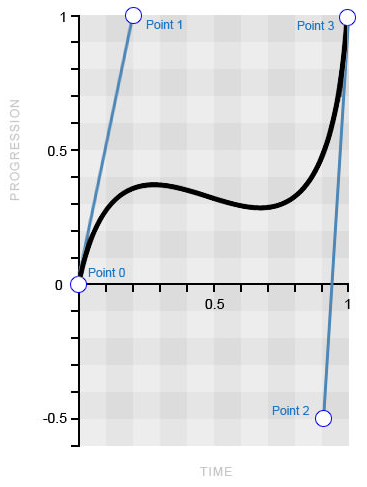
Кривая безье со значениями за пределами
0-1 (изображение принадлежит Smashing Magazine)Точка 2 расположена за пределами обычного промежутка
0-1 на -0,5, что в свою очередь тянет кривую вниз. Посмотрите следующее демо и вы увидите эффект «подпрыгивания» в середине анимации.
Исходная анимация на Codepen
И наоборот, вы могли бы разместить это «движение назад» в начале анимации, а также заставить кривую немного «выбежать» за предполагаемую конечную точку. Представьте, будто вы делаете пару шагов назад для разбега; затем, в конце, вы проноситесь мимо финиша, в результате чего вам приходится немного вернуться, чтобы узнать время, которое показал хронометр. Посмотрите пример, чтобы действительно понять, о чем идет речь. Кроме того, изучите кривую Безье, которая создает такой эффект.

Исходная анимация на Codepen
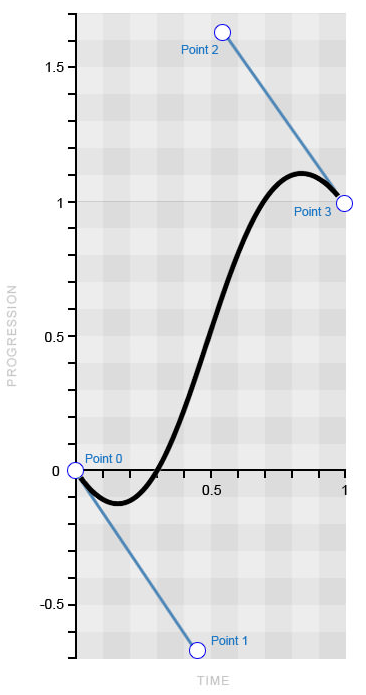
Кривая Безье со значениями за пределами
0-1 (изображение принадлежит Smashing Magazine)Теперь у вас должно быть вполне ясное представление о том, как значения
cubic-bezier() за пределами 0-1 могут физически повлиять на поведение анимации. Мы, конечно, можем глазеть на перемещающиеся кубики целый день, но давайте таки закончим данный раздел примером, который ясно покажет изобретательский подход в использовании временной функции.
Исходная анимация на Codepen
Всё верно: мы анимируем воздушный шарик! Чего?.. То ли это, что вам всегда хотелось делать с помощью CSS?
Суть анимации в «надувании» шарика по клику таким образом, что он взлетит к «потолку» и слегка отскочет от него, как по-настоящему. Значение
cubic-bezier() за границей 0-1 и есть тот инструмент, который позволит нам создать этот эффект «отскока», повторяя реалистичное поведение. В представленном фрагменте кода показаны координаты, выставленные в функции cubic-bezier(), а далее показана полученная кривая./* The cubic-bezier() values for the bouncing balloon */
transition-timing-function: cubic-bezier(.65, 1.95, .03, .32);
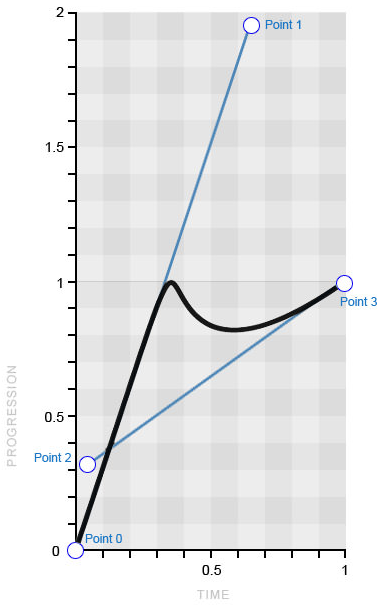
Кривая Безье, эмулирующая «отскакивающий» шарик (изображение принадлежит Smashing Magazine)
Данный пример отлично показывает, как кривая трансформируется в итоговую анимацию, поскольку кривая отражает её практически идеально. Сначала кривая проходит от начала шкалы прогрессии по прямой, заставляя шарик двигаться от её начала до конца с одинаковой скоростью. Затем, подобно замедлению шарика, кривая резко изгибается в обратном направлении, прежде чем начать постепенно возвращаться к вершине. На самом деле всё очень просто!
Так что как только вы освоите кривую и искусство манипулирования ею, будете умницей!
Временные функции и покадровая анимация CSS
Перед тем, как мы пойдем дальше, следует упомянуть о поведении временных функций при использовании их в покадровой анимации. Общий смысл тот же (в сравнении с переходами [transition]), однако есть одно исключение, которое стоит запомнить: когда вы применяете временную функцию к нескольким кадрам, она выполняется на каждом отдельном кадре, нежели на протяжении всей анимации.
То есть, если у вас имеется четыре кадра, которые перемещают квадрат от одного угла к другому внутри контейнера, и вы применяете временную функцию с «отскоком» (такую же, как мы использовали для шарика), каждое из четырех движений будет подвержено этому «отскоку», нежели вся анимация. Давайте посмотрим это поведение в действии и в коде.

Исходная анимация на Codepen (гифка получилась кривоватой)
@keyframes square {
25% {
top:200px;
left:0;
}
50% {
top:200px;
left:400px;
}
75% {
top:0;
left:400px;
}
}
div {
animation: square 8s infinite cubic-bezier(.65, 1.95, .03, .32);
top: 0;
left: 0;
/* Other styles */
}
Обратите внимание на то, что когда кадр
100% не определен, элемент просто возвращается к своему начальному состоянию. В данном случае это то, что нам нужно, поэтому определять этот кадр мы не будем. Из примера вполне ясно видно работу временной функции на всех четырех кадрах по тому, как квадрат на каждом из них отскакивает от стенок рамки.Если для какого-либо конкретного кадра вам необходимо определить собственную временную функцию, то определите её прямо в коде этого кадра, как показано в следующем примере:
@keyframes square {
50% {
top: 200px;
left: 400px;
animation-timing-function: ease-in-out;
}
}
Временная функция steps()
Вы думали, что на этом наши приключения окончены? Как бы не так! Я ведь уже говорил вам, что CSS не ограничивается встроенными временными функциями!
В данном разделе мы изучим концепцию «пошаговых» функций и заменим кривые прямыми линиями с помощью временной функции
steps.Данная функция весьма полезна, несмотря на свою специфичность. Она позволяет разбить анимацию на отрезки, что будет отличать её от обычного анимированного движения. Например, если нам надо переместить квадрат на 400 пикселей вправо за 4 шага в течение 4 секунд, то вместо плавного движения он будет «прыгать» на 100 пикселей каждую секунду. А теперь давайте взглянем на код данного примера. Он, должно быть, просто дуновение свежести после погружения в тонкости функции
cubic-bezier()!
Исходная анимация на Codepen
div {
transition: 4s steps(4);
}
div:target {
left: 400px;
}
Как видите, все дело в определении количества отрезков анимации. Но имейте в виду, что оно не может быть отрицательным или десятичным числом. Есть и второй, не обязательный, аргумент, возможные значения которого —
start и end (последнее является значением по умолчанию).transition-timing-function: steps(4, start);
transition-timing-function: steps(4, end);
Значение start запускает анимацию в начале каждого шага, а end — в конце. Применительно к «движущемуся квадрату», данная картинка поможет лучше объяснить разницу между двумя этими значениями.
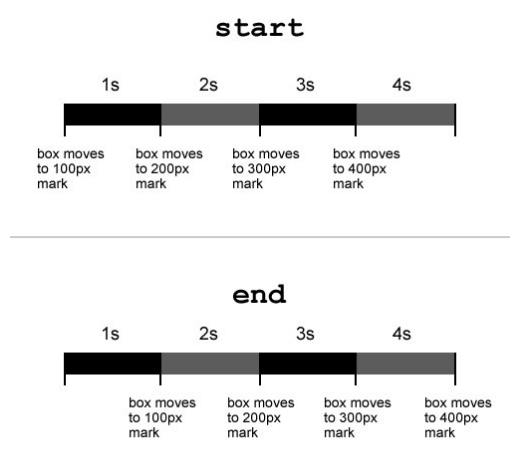
Различие значений
start и end функции steps() (изображение принадлежит Smashing Magazine)Как видите, со значением
start анимация начинается немедленно, а при end — с задержкой в одну (в данном случае) секунду.Ну, и ради пущей всеобъемлющности материала, отметим, что у функции
step() есть два предопределенных аргумента: step-startи step-end, эквивалентные записи steps(1, start) и steps(1, end) соответственно.Изобретательный подход к «пошаговым» функциям
Наверняка из повседневных задач вам вряд ли так уж часто будет выпадать анимация движущегося квадрата, тем не менее с помощью функции
steps() можно сделать уйму других крутых штук. Допустим, если в вашем распоряжении имеется несколько мультяшных спрайтов, то вы можете использовать уже изученную технику для создания анимации, используя всего пару CSS свойств! Давайте посмотрим на демо и код.
Исходная анимация на Codepen
div {
width: 125px;
height: 150px;
background: url(images/sprite.jpg) left;
transition: 2s steps(16);
/* The number of steps = the number of frames in the cartoon */
}
div:target {
background-position: -2000px 0;
}
Итак, у нас есть прямоугольник 125 пикселей в ширину с фоновым изображением на 2 000 пикселей, содержащим 16 кадров. Изначально это изображение расположено по левому краю прямоугольника, и всё, что нам предстоит сделать, — сдвигать его влево так, чтобы все 16 кадров прошли через маленькое «окошко» нашего прямоугольника. При «обычной» анимации кадры просто пролетели бы мимо, однако с функцией
steps() фоновое изображение сдвигается влево ровно за 16 шагов, в достаточной мере показывая каждый кадр изображения. Вот так мы сделали мини-мультик всего лишь с помощью CSS анимаций!
Демонстрация способа смещения фонового изображения так, что каждый кадр пройдет через небольшое «окошко» (изображение принадлежит Smashing Magazine)
Еще одно забавное использование функции
steps() я нашел благодаря Лиа Веру (кому же еще?), которая придумала весьма интересную анимацию компьютерного набора. О ней я вам сейчас и расскажу.
Исходная анимация на Codepen
Для начала, вам нужен какой-то текст. А также, к сожалению, вам необходимо знать, сколько символов он содержит, ибо вам придется использовать это количество в CSS. Еще одно условие: шрифт должен быть моноширинным для того, чтобы все символы имели одинаковую ширину.
<p>smashingmag</p>
.text {
width: 6.6em;
width: 11ch; /* Number of characters */
border-right: .1em solid;
font: 5em monospace;
}
Наш текст состоит из 11 символов. Длину строки мы укажем с помощью единицы измерения
ch, а для браузеров, не имеющих её поддержки, мы напишем другое значение. Далее по правой стороне строки мы поставим черную рамку, которая станет курсором. И теперь, когда всё на месте, нам нужно лишь анимировать текст, а это чрезвычайно просто.Нам понадобятся две отдельные анимации: одна для курсора, другая для печати. Чтобы сделать курсор, необходимо всего лишь заставить мерцать черную рамку.
@keyframes cursor {
50% {
border-color: transparent;
}
}
.text {
/* existing styles */
animation: cursor 1s step-end infinite;
}
Как и предполагалось, рамка просто меняет свой цвет с черного на прозрачный и обратно. В данном случае функция
steps() имеет определенный смысл: уберите её, и курсор, вместо того, чтобы «моргать», будет плавно появляться и исчезать.Наконец, анимация печатания столь же проста. Всё, что нам нужно сделать, — уменьшить длину строки до нуля, а затем постепенно наращивать её за 11 шагов (по количеству символов).
@keyframes typing {
from {
width: 0;
}
}
.text {
/* existing styles */
animation: typing 8s steps(11),
cursor 1s step-end infinite;
}
Текст будет «раскрываться» по одной букве за шаг в течении восьми секунд, в то время как «курсор» (
border-right) будет мигать постоянно. Техника проста настолько же, насколько и эффективна.Теперь мы можем дополнить этот замечательный пример, попробовав обратный эффект — удаление текста. Для этого нужно изменить ключевое слово кадра с
from на to и затем добавить параметр animation-fill-mode со значением forwards, чтобы удостовериться, что когда текст «удалится» (т. е. когда анимация завершится), он останется «удаленным». Посмотрите на демо.
Исходная анимация на Codepen
<div id="go">
<p class="text">smashingmag</p>
</div>
@-webkit-keyframes typing { to { width: 0; } }
@keyframes typing { to { width: 0; } }
@-webkit-keyframes cursor { 50% { border-color: transparent; } }
@keyframes cursor { 50% { border-color: transparent; } }
.text {
width: 6.6em;
width: 11ch; /* Number of characters */
border-right: .1em solid;
overflow: hidden;
font: 5em monospace;
margin-top: 50px;
-webkit-animation: cursor 1s step-end infinite;
animation: cursor 1s step-end infinite;
}
#go:target .text {
-webkit-animation: typing 4s steps(11) forwards,
cursor 1s step-end infinite;
animation: typing 4s steps(11) forwards,
cursor 1s step-end infinite;
}
Недостатком обоих примеров, показанных в этом разделе, является тот факт, что вы должны знать заранее количество кадров или символов для того, чтобы указать правильное количество шагов анимации. Если их количество изменится, вам придется изменить и код. Несмотря на это, мощь функции
steps() видна невооруженным взглядом, как и поистине фантастическая функциональность временных функций CSS в целом.Поддержка браузерами
Понятное дело, что вы не сможете использовать временные функции CSS, если браузер не поддерживает CSS переходы и покадровую анимацию. К счастью, в наши дни поддержка осуществляется весьма неплохо.
ПОДДЕРЖКА CSS TRANSITIONS
| Браузер | С префиксом | Без префикса |
| Internet Explorer | Нет | 10+ |
| Firefox | 4+ (-moz-) |
16+ |
| Chrome | 4+ (-webkit-) |
26+ |
| Safari | 3.1+ (-webkit-) |
6.1+ |
| Opera | 10.5+ (-o- prefix) |
12.1+ |
Несмотря на то, что все новейшие версии браузеров откинули префиксы для переходов, все-таки было бы не лишним дополнительно прописывать свойства с префиксом
-webkit- для поддержки устаревших мобильных браузеров. В то же время, с точки зрения прогрессивного улучшения, я думаю, что необходимость использования префиксов -moz- и -o- уже прошла.ПОДДЕРЖКА ВРЕМЕННЫХ ФУНКЦИЙ CSS
| Браузер | С префиксом | Без префикса |
| Internet Explorer | Нет | 10+ |
| Firefox | 5+ (-moz-) |
16+ |
| Chrome | 4+ (-webkit-) |
Не поддерживается |
| Safari | 4+ (-webkit-) |
Не поддерживается |
| Opera | 12 (-o- prefix), 15+ (-webkit- prefix) |
Только 12.1 (не поддерживается после перехода на WebKit) |
Несмотря на то, что кое-кому понадобилось больше времени, чтобы осуществить поддержку всех возможностей временных функций, несложно заметить, что в данное время этот функционал реализован во всех современных браузерах.
Итог
Так что же мы узнали о временных функциях CSS? Давайте подытожим.
- Они определяют, когда анимация ускоряется и замедляется
- Они гораздо круче, нежели набор предопределенных значений
- Вы можете создавать эффект «отскока» с помощью значений cubic-bezier(), выходящих за пределы промежутка 0-1
- Вы можете разбить анимацию на несколько шагов/отрезков
- Поддержка браузерами великолепна и только улучшается
И, несмотря на кросс-платформенность описанных технологий, это не было бы статьей о техниках CSS 3, если бы я не упомянул о прогрессивном улучшении. Всегда идите от простого к сложному: убедитесь, что ваша работа доступна на устройствах и в браузерах, которые не поддерживают данный функционал, перед тем, как создавать эффекты для браузеров, которые смогут их обработать.
А теперь вперед! Счастливых шажков и искривлений!