Все началось с данного топика на сайте gamedev.ru. Топикстартер предложил найти сортировку, которая обладает следующими свойствами:
Оговорки на все три ограничения:
Вся информация, которую мы знаем об элементах массива — это то, что они все образуют линейно упорядоченное множество. Все, что мы можем делать — это сравнивать два элемента массива (за O(1)) и менять их местами (тоже за O(1)).
Под катом можно узнать, что в итоге получилось у нас.
Challenge. Прежде чем заглядывать под кат, предлагаю сначала самостоятельно подумать над алгоритмом. Если придумается что-то круче нашего варианта — напишите в комментариях.
Оговорюсь, что тщательного поиска по статьям произведено не было — возможно, мы повторно открыли какой-нибудь уже известный алгоритм, или же алгоритм, которые решают данную задачу, уже давно известен (возможно, гораздо эффективнее нашего).
Практическое применение нашего алгоритма вряд ли возможно, задача имеет скорее академический интерес.
Известные сортировки, которые сразу приходят на ум, не удовлетворяют всем трем пунктам одновременно, например:
В первом же комментарии товарищем FordPerfect был предложен не очень известный в широких кругах алгоритм Median of Medians. Другое его название BFPRT от фамилий ученых, его придумавших: Мануель Блюм, Роберт В. Флойд, Вон Пратт, Рональд Л. Ривест и Роберт Е. Тарьян. Алгоритм описан на википедии (ru, en), а также в Кормене, но я немного расскажу про него, поскольку на википедии он описан настолько топорно, что я понял его суть только после сопоставления русской и английской версии (и еще пришлось заглянуть в оригинальную статью). Да и на Хабре его описания еще не было. В Кормене, если что, описание нормальное, но то, что этот алгоритм там есть — я узнал уже позже. Если вы уже знаете этот алгоритм — данный кусочек статьи можно пропустить.
Алгоритм Median of Medians позволяет найти k-ую порядковую статистику на любом массиве за линейное время в худшем случае. В библиотеке C++ STL имеется похожий алгоритм std::nth_element, который тоже находит k-ую порядковую статистику за линейное время, но в среднем, поскольку в его основе лежит алгоритм Quickselect. Последний по сути представляет собой quick sort, в котором на каждом шаге мы спускаемся только по одной ветви рекурсии (подробнее про Quickselect можно почитать здесь и здесь). Median of Medians является модификацией алгоритма Quickselect и не допускает выбора плохого элемента для «ветвления», который в худшем случае приводит к квадратичному времени работы.
Зачем нам нужен этот Median of Medians? Да все довольно просто — с его помощью можно за линейное время найти медиану массива (n/2-ую порядковую статистику) и именно по этому элементу ветвить алгоритм быстрой сортировки. Это приведет к тому, что quick sort будет работать за O(nlogn) не в среднем, а в худшем случае.
Описание алгоритма Median of Medians. Входные данные: массив (заданный, например, первым и последним элементами списка) и число k — какой по счету элемент нам требуется найти.
Рассмотрим на примере что тут происходит. Пусть имеется массив и мы хотим найти его медиану:

Тут 27 различных чисел от 1 до 27. Мы ищем 14-ый по счету элемент. Разобьем элементы на блоки длины 5 и отсортируем числа внутри каждого блока:

Медианы каждого блока выделены желтым. Перемещаем их в начало массива и рекурсивно запускаем наш алгоритм для поиска медианы в нем:

Я не буду расписывать что там происходит внутри рекурсии, ясно одно — искомой медианой будет число 12.

Это число 12 — опорный элемент или медиана медиан — обладает следующим замечательным свойством. Давайте вернемся на пару картинок назад и мысленно переместим наши блоки следующим образом:
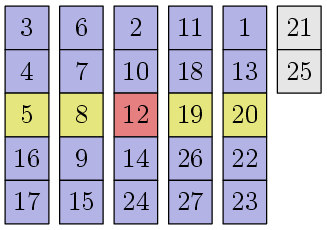
Все столбики отсортированы по среднему элементу, плюс элементы в каждом столбике тоже отсортированы. Мы можем видеть, что примерно 30% элементов (3/10n + O(1), если быть точным), которые выше и левее опорного элемента, не больше, чем он. Аналогично для примерно 30% элементов ниже и правее опорного элемента — они не меньше, чем он. Это означает, что когда мы осуществим процедуру разделения, примерно 30% всех элементов обязательно окажутся левее опорного элемента и примерно 30% — правее:

На самом деле, тут небольшая неточность: нам повезло с тем, что элементов, равных опорному, ровно одна штука. Если таких элементов много, то они все образуют целый блок и куда именно встанет опорный элемент — непонятно. Но это и не важно на самом деле. Мы знаем, что элементов, которые не меньше опорного элемента, — не менее 30%, значит элементов, которые строго меньше опорного элемента, — не более 70%. Аналогично — элементов, которые строго больше опорного элемента тоже не более 70%. Таким образом, размеры первого и третьего блоков из описания алгоритма выше всегда будут иметь длину не более 7/10n+O(1)!

Продолжим разбор примера. После процедуры разделения становится понятно, что наш 14-ый элемент находится в третьем блоке, поэтому мы рекурсивно запускаем для него весь алгоритм, но теперь ищем в нем уже 2-ой элемент.
Какова сложность рассмотренного нами алгоритма?
Пусть T(n) — число операция алгоритма Median of Medians в худшем случае для массива длины n. На каждом шаге алгоритм дважды рекурсивно вызывает самого себя. Первый раз — для нахождения медианы медиан на массиве длиной n/5 + O(1) элементов. Второй раз — уменьшая пространство поиска, при этом в худшем случае размер массива уменьшается до 7/10n + O(1). Все остальные операции требуют линейного времени. Итого получаем соотношение:
T(n) = T(2/10n) + T(7/10n) + Cn, где C — некоторая константа.
Разложим это соотношение:
T(n) = Cn + (2/10+7/10)Cn + (2/10+7/10)(2/10+7/10)Cn +… = Cn * ∑i=0..∞ (9/10)i = 10Cn = O(n)
Отлично! Алгоритм имеет линейную сложность!
Median of Medians несложно реализовать на списках с использованием рекурсии, что дает нам хорошее частичное решение изначальной задачи: гарантированная сортировка за O(nlogn) на односвязном списке с использованием O(logn) памяти.
Код.
Давайте теперь избавляться от рекурсии.
Для начала давайте уберем рекурсию из, собственно, быстрой сортировки. Как это сделать — не совсем очевидно, поэтому в данном разделе мы рассмотрим как это сделать.
В данном разделе будет описана идея, которую предложил на форуме gamedev.ru товарищ FordPerfect (да, по сути все идеи данной статьи не мои — я просто разместил объяву). Первоисточник идеи неизвестен, гугл по этому поводу по большей части молчит и выдает много ссылок на так называемый iterative quicksort, где сплошь и рядом эмулируется стек (впрочем, тут нашлось обсуждение похожей идеи), а сам FordPerfect говорит, что ее придумал его одногруппник за 40 минут раздумий над задачей «quicksort с O(1) памяти». Название «Flat quick sort» тоже самопальное, возможно этот алгоритм известен под другим названием.
Давайте вспомним как работает обычная рекурсивная быстрая сортировка. Входные данные: массив, заданный, например, двумя итераторами на начальный и конечный элементы односвязного списка.
Информация, которую нам надо запоминать по ходу рекурсии — это где начинается и заканчивается третий блок.
Заметим следующую вещь: любой элемент первого блока меньше любого элемента второго блока, а любой элемент второго блока меньше любого элемента третьего блока.
Идея в следующем: давайте в каждом блоке переместим самый большой элемент в начало блока. Тогда мы сможем однозначно определять где начнется следующий блок! Для этого мы просто будем идти от начала блока до тех пор, пока не встретим элемент строго больше — он будет сигнализировать о начале следующего блока!
Теперь алгоритм быстрой сортировки можно переписать следующим образом:
Теперь рассмотрим этот алгоритм на примере:

Где-то я уже видел этот массив… Давайте расставим указатели X, Y и Z:

Блок X-Z не отсортирован. Тогда найдем медиану:

Мы предполагаем, что процедура поиска медианы перемешивает элементы самым причудливым образом, оставляя саму медиану в самом начале (для наглядности примера! реализация может, например, возвращать итератор на элемент, который является медианой). Хорошо, давайте теперь выполним процедуру разделения:

Получились 3 блока. Блокофицируем последний блок и переместим Z в конец первого блока:

Теперь начинаем все с начала. Текущий блок X-Z не отсортирован, значит ищем в нем медиану:

Выполняем процедуру разделения:

Блокофицируем третий блок и перемещаем Z в конец первого блока:

Опять смотрим на X-Z:

Нам повезло! Блок отсортирован, поэтому его можно оставить в покое и искать следующий блок. Указатели X и Z переместятся следующим образом:

Внезапно, данный блок тоже отсортирован, поскольку это второй блок предыдущего шага. Ищем следующий блок:

Проверяем на упорядоченность — увы, на это раз не повезло, придется упорядочивать. Находим медиану, а потом делаем процедуру разделения:


Далее, мы перейдем к блоку [8,9], он отсортирован, поэтому X и Z сдвинутся на блок [10], который тоже отсортирован, после чего алгоритм будет рассматривать блок [13, 11, 12], в котором все уже совсем тривиально. Разбор сортировки второй половины массива предлагается выполнить читателю самостоятельно.
Код.
К сожалению, с Median of Medians такой фокус, как использование максимального элемента для идентификации блоков в flat quick sort, не пройдет, ибо элементы массива каждый раз перемешиваются непонятно каким образом. Здесь мы будем использовать другой фокус.
На самом деле, чтобы заставить quick sort работать за гарантированные O(nlogn), не обязательно находить точную медиану для этапа разделения. Достаточно найти что-то приблизительное. Если дать гарантию, что первый и третий блок после этапа разделения не будут превосходить Cn для некоторого конкретного С<1, quick sort будет работать за O(nlogn). Даже для C=0.99. Слютой бешеной скрытой константой, но O(nlogn)!
Поэтому мы модифицируем Median of Medians так, чтобы он находил медиану с некоторой погрешностью K = O(log2n). То есть будет найден элемент, порядковый номер которого где-то в границах от n/2-K/2 до n/2+K/2. Поскольку K порядка степени логарифма, легко найдется такое (конкретное) n, начиная с которого отрезок [n/2-K/2, n/2+K/2] будет лежать, скажем, между 1/4n и 3/4n. Для всех меньших n сортировать можно просто пузырьком.
Почему K = O(log2n)? Да мы просто используем K элементов массива для того, чтобы хранить в них всю необходимую информацию по стеку (идея, опять же, товарища FordPerfect). Уровней рекурсии O(logn), на каждом из них нам нужно сохранить O(1) чисел на O(logn) бит. А медиану для quick sort найдем среди оставшихся N-K элементов.
Каждый бит представляется двумя последовательными различными элементами массива. Если первый из них меньше второго — бит хранит состояние 0, иначе — 1 (или наоборот). Первая задача, которую нам нужно решить — это найти K/2 пар различных элементов массива и понять что делать если столько пар не найдется.
Делается это очень просто. Пусть итераторы X и Y указывают на первый элемент массива. Будем двигать Y вперед пока не найдем элемент, не равный X. Если нашли — подвинем X вперед, поменяем местами элементы, на которые указывают X и Y, подвинем X еще раз вперед (+ еще надо обработать мелкий случай — подвинуть Y вперед, если он оказался перед X). И так пока не найдем K/2 пар. Что если Y уже дошел до конца массива, а K/2 пар еще не нашлись? Это означает, что все элементы от X до Y включительно одинаковые! (Довольно просто проверить, что этот инвариант сохраняется на протяжении выполнения всего алгоритма). Тогда в качестве опорного элемента можно сразу выбрать один из этих элементов. Если выбрать K < n/2, этот опорный элемент будет точной медианой.
Теперь вопрос: а не поломает ли работа со стеком асимптотику алгоритма? Это очень хороший вопрос, поскольку на первый взгляд кажется, что вершин в нашем рекурсивном дереве порядка O(n) и на каждую вершину нам надо O(log2n) операций со стеком. Неужели асимптотика ухудшается до O(nlog2n) для нашего Median of Medians (и до O(nlog3n) для всего алгоритма)? Тут все несколько сложнее.
Чтобы посчитать точное число вершин в дереве надо решить следующую рекурренту:
N(n) = N(n/5) + N(7N/10) + 1
N(n) = 1 для n<C
Что-то подобное можно было видеть выше, но замена Cn на 1 делает рекурренту несколько более сложной для вычисления. На помощь приходит метод Акра-Бацци. Наша рекуррента подходит всем условиям и после всех соответствующих подстановок получаем, что число вершин N(n) растет как O(n0.84) (Θ(n0.839780...) если быть более точным). Итого временная сложность алгоритма составляет O(n + n0.84log2n) = O(n).
Дальнейшее расписывание алгоритма я считаю излишним, нужно просто реализовать то, что было описано в одной из предыдущих глав статьи. Лучше сразу глянуть в код. Картинок тоже не будет — чтобы алгоритм вообще заработал, нужно довольно большое число элементов в массиве. Какое именно? Об этом чуть ниже.
Насколько непрактичен предложенный алгоритм? Вот некоторые выкладки:
Пусть мы хотим получить отклонение не более 1/4n от настоящей медианы (то есть K < n/2). Тогда нам надо забить стек на 3[logn] уровней рекурсии (тут log — двоичный, 3 из-за того, что (3/4)3 < 0.5, а [x] — это округление числа x вверх до ближайшего целого). На каждый уровень рекурсии нам надо 2[logn] бит — надо хранить текущую длину массива, какой по порядку элемент мы ищем сейчас (это число всегда укладывается в [logn]-1 бит) и еще один бит на поддержание порядка обхода дерева рекурсии (надо помнить из какой ветви рекурсии мы вернулись). На каждый бит 2 элемента, итого надо 12[logn]2 элементов под стек.
Теперь решаем уравнение: 12[logn]2 < n/2 или 24[logn]2 < n. Надо найти такое n', что для любого n>=n' 24[logn]2 < n. Такое n' порядка 3500. То есть для n<3500 надо сортировать пузырьком.
Предел для n, начиная с которого K всегда не превышает n — 1500, то есть для n<1500 сортировка даже не заработает (не хватит элементов для эмуляции стека), тут уже без раздумий надо пользоваться пузырьком. Впрочем, если поиграться константами, то, вероятно, можно эту оценку улучшить.
Код.
Все ссылки на код по всей статье в одном месте:
- Время выполнения — гарантированные O(nlogn).
- Использование O(1) дополнительной памяти.
- Применимость для сортировки данных в односвязных списках (но не ограничиваясь ими).
Оговорки на все три ограничения:
- Гарантированные O(nlogn) означают, что, например, среднее время быстрой сортировки не подходит — должно получаться O(nlogn) для любых, даже самых худших входных данных.
- Рекурсию использовать нельзя, поскольку она подразумевает O(logn) памяти на хранение стека рекурсивных вызовов.
- Произвольного доступа к элементам сортируемого массива нет, мы можем двигаться итератором от любого элемента только к соседнему (за O(1)), причем только в одном направлении (вперед по списку). Модифицировать сам список (перевешивать указатели на следующие элементы) нельзя.
Вся информация, которую мы знаем об элементах массива — это то, что они все образуют линейно упорядоченное множество. Все, что мы можем делать — это сравнивать два элемента массива (за O(1)) и менять их местами (тоже за O(1)).
Под катом можно узнать, что в итоге получилось у нас.
Challenge. Прежде чем заглядывать под кат, предлагаю сначала самостоятельно подумать над алгоритмом. Если придумается что-то круче нашего варианта — напишите в комментариях.
Оговорки
Оговорюсь, что тщательного поиска по статьям произведено не было — возможно, мы повторно открыли какой-нибудь уже известный алгоритм, или же алгоритм, которые решают данную задачу, уже давно известен (возможно, гораздо эффективнее нашего).
Практическое применение нашего алгоритма вряд ли возможно, задача имеет скорее академический интерес.
Сбор информации
Известные сортировки, которые сразу приходят на ум, не удовлетворяют всем трем пунктам одновременно, например:
- Пузырьковая сортировка (bubble sort) подходит под пункты 2 и 3, но работает за O(n2).
- Быстрая сортировка (quick sort) удовлетворяет пунктам 2 и 3 (пункт 2 — со знанием кое-какой идеи), но для пункта 1 дает O(nlogn) времени лишь в среднем и существуют входные данные, на которых она будет работать за O(n2).
- Сортировка кучей (heap sort) удовлетворяет ограничениям 1 и 2, но, к сожалению, требует произвольный доступ к памяти.
- Сортировка слияниями (merge sort) подходит под ограничения 1 и 3, однако требует O(n) дополнительной памяти.
- Сортировка слияниями на месте (in-place merge sort) укладывается в ограничения 1 и 2 (есть даже ее stable вариант, но там жесть), но совершенно непонятно, как ее эффективно реализовать без произвольного доступа к памяти.
Median of Medians или алгоритм BFPRT
В первом же комментарии товарищем FordPerfect был предложен не очень известный в широких кругах алгоритм Median of Medians. Другое его название BFPRT от фамилий ученых, его придумавших: Мануель Блюм, Роберт В. Флойд, Вон Пратт, Рональд Л. Ривест и Роберт Е. Тарьян. Алгоритм описан на википедии (ru, en), а также в Кормене, но я немного расскажу про него, поскольку на википедии он описан настолько топорно, что я понял его суть только после сопоставления русской и английской версии (и еще пришлось заглянуть в оригинальную статью). Да и на Хабре его описания еще не было. В Кормене, если что, описание нормальное, но то, что этот алгоритм там есть — я узнал уже позже. Если вы уже знаете этот алгоритм — данный кусочек статьи можно пропустить.
Алгоритм Median of Medians позволяет найти k-ую порядковую статистику на любом массиве за линейное время в худшем случае. В библиотеке C++ STL имеется похожий алгоритм std::nth_element, который тоже находит k-ую порядковую статистику за линейное время, но в среднем, поскольку в его основе лежит алгоритм Quickselect. Последний по сути представляет собой quick sort, в котором на каждом шаге мы спускаемся только по одной ветви рекурсии (подробнее про Quickselect можно почитать здесь и здесь). Median of Medians является модификацией алгоритма Quickselect и не допускает выбора плохого элемента для «ветвления», который в худшем случае приводит к квадратичному времени работы.
Зачем нам нужен этот Median of Medians? Да все довольно просто — с его помощью можно за линейное время найти медиану массива (n/2-ую порядковую статистику) и именно по этому элементу ветвить алгоритм быстрой сортировки. Это приведет к тому, что quick sort будет работать за O(nlogn) не в среднем, а в худшем случае.
Описание алгоритма Median of Medians. Входные данные: массив (заданный, например, первым и последним элементами списка) и число k — какой по счету элемент нам требуется найти.
- Если массив достаточно маленький (меньше 5 элементов) — в лоб сортируем его пузырьком и возвращаем k-ый элемент.
- Разбиваем все элементы массива на блоки по 5 элементов. На возможный неполный последний блок пока не обращаем внимания.
- В каждом блоке сортируем элементы пузырьком.
- Выделяем подмассив из средних (третьих) элементов каждого блока. Можно их просто перенести в начало массива.
- Рекурсивно запускаем Median of Medians для этих [n/5] элементов и найходим их медиану (n/10-ый элемент). Этот элемент назовет опорным (pivot element).
- Делаем процедуру разделения, вероятно всем знакомую по алгоритмам quick sort и quickselect: перемещаем все элементы меньше опорного в начало массива, а все элементы больше — в конец. Элементы из возможного неполного блока в конце массива тоже учитываем. Итого, получаем три блока: элементы меньше опорного, равные ему и больше него.
- Определяем в каком из блоков нам нужно искать наш k-ый элемент. Если он во втором блоке — возвращаем любой элемент оттуда (они все равно все одинаковые). Иначе рекурсивно запускаем Median of Medians для этого блока с возможной поправкой на номер элемента: для третьего блока нужно из числа k вычесть длины предыдущих блоков.
Рассмотрим на примере что тут происходит. Пусть имеется массив и мы хотим найти его медиану:

Тут 27 различных чисел от 1 до 27. Мы ищем 14-ый по счету элемент. Разобьем элементы на блоки длины 5 и отсортируем числа внутри каждого блока:

Медианы каждого блока выделены желтым. Перемещаем их в начало массива и рекурсивно запускаем наш алгоритм для поиска медианы в нем:

Я не буду расписывать что там происходит внутри рекурсии, ясно одно — искомой медианой будет число 12.

Это число 12 — опорный элемент или медиана медиан — обладает следующим замечательным свойством. Давайте вернемся на пару картинок назад и мысленно переместим наши блоки следующим образом:

Все столбики отсортированы по среднему элементу, плюс элементы в каждом столбике тоже отсортированы. Мы можем видеть, что примерно 30% элементов (3/10n + O(1), если быть точным), которые выше и левее опорного элемента, не больше, чем он. Аналогично для примерно 30% элементов ниже и правее опорного элемента — они не меньше, чем он. Это означает, что когда мы осуществим процедуру разделения, примерно 30% всех элементов обязательно окажутся левее опорного элемента и примерно 30% — правее:

На самом деле, тут небольшая неточность: нам повезло с тем, что элементов, равных опорному, ровно одна штука. Если таких элементов много, то они все образуют целый блок и куда именно встанет опорный элемент — непонятно. Но это и не важно на самом деле. Мы знаем, что элементов, которые не меньше опорного элемента, — не менее 30%, значит элементов, которые строго меньше опорного элемента, — не более 70%. Аналогично — элементов, которые строго больше опорного элемента тоже не более 70%. Таким образом, размеры первого и третьего блоков из описания алгоритма выше всегда будут иметь длину не более 7/10n+O(1)!

Продолжим разбор примера. После процедуры разделения становится понятно, что наш 14-ый элемент находится в третьем блоке, поэтому мы рекурсивно запускаем для него весь алгоритм, но теперь ищем в нем уже 2-ой элемент.
Какова сложность рассмотренного нами алгоритма?
Пусть T(n) — число операция алгоритма Median of Medians в худшем случае для массива длины n. На каждом шаге алгоритм дважды рекурсивно вызывает самого себя. Первый раз — для нахождения медианы медиан на массиве длиной n/5 + O(1) элементов. Второй раз — уменьшая пространство поиска, при этом в худшем случае размер массива уменьшается до 7/10n + O(1). Все остальные операции требуют линейного времени. Итого получаем соотношение:
T(n) = T(2/10n) + T(7/10n) + Cn, где C — некоторая константа.
Разложим это соотношение:
T(n) = Cn + (2/10+7/10)Cn + (2/10+7/10)(2/10+7/10)Cn +… = Cn * ∑i=0..∞ (9/10)i = 10Cn = O(n)
Отлично! Алгоритм имеет линейную сложность!
Median of Medians несложно реализовать на списках с использованием рекурсии, что дает нам хорошее частичное решение изначальной задачи: гарантированная сортировка за O(nlogn) на односвязном списке с использованием O(logn) памяти.
Код.
Давайте теперь избавляться от рекурсии.
Flat quick sort
Для начала давайте уберем рекурсию из, собственно, быстрой сортировки. Как это сделать — не совсем очевидно, поэтому в данном разделе мы рассмотрим как это сделать.
В данном разделе будет описана идея, которую предложил на форуме gamedev.ru товарищ FordPerfect (да, по сути все идеи данной статьи не мои — я просто разместил объяву). Первоисточник идеи неизвестен, гугл по этому поводу по большей части молчит и выдает много ссылок на так называемый iterative quicksort, где сплошь и рядом эмулируется стек (впрочем, тут нашлось обсуждение похожей идеи), а сам FordPerfect говорит, что ее придумал его одногруппник за 40 минут раздумий над задачей «quicksort с O(1) памяти». Название «Flat quick sort» тоже самопальное, возможно этот алгоритм известен под другим названием.
Давайте вспомним как работает обычная рекурсивная быстрая сортировка. Входные данные: массив, заданный, например, двумя итераторами на начальный и конечный элементы односвязного списка.
- Проверка за один проход: если массив уже отсортирован, то делать нечего — выходим.
- Выбираем элемент (pivot) для процедуры разделения — обычно случайно, но для нашего случая — медиану с помощью алгоритма Median of Medians.
- Творим процедуру разделения — получаем три блока: элементы, что меньше, чем pivot; элементы, что равны ему; и элементы больше.
- Рекурсивно запускаем быструю сортировку для первого и третьего блоков.
Информация, которую нам надо запоминать по ходу рекурсии — это где начинается и заканчивается третий блок.
Заметим следующую вещь: любой элемент первого блока меньше любого элемента второго блока, а любой элемент второго блока меньше любого элемента третьего блока.
Идея в следующем: давайте в каждом блоке переместим самый большой элемент в начало блока. Тогда мы сможем однозначно определять где начнется следующий блок! Для этого мы просто будем идти от начала блока до тех пор, пока не встретим элемент строго больше — он будет сигнализировать о начале следующего блока!
Теперь алгоритм быстрой сортировки можно переписать следующим образом:
- Создадим указатели X и Y. Пусть указатель X указывает на начало массива, а указатель Y — на его конец. Еще создадим указатель Z, который будет указывать на конец текущего блока. Изначально Z=Y.
- Бесконечно выполняем следующие действия:
- Если текущий блок X-Z уже отсортирован — ищем следующий блок. Перемещаем X на элемент, следующий после Z. Если X переместить нельзя, поскольку Z=Y — выходим из цикла. Теперь ищем ближайший элемент a после X, который больше элемента, на который указывает X. Если такого нет — делаем Z=Y, иначе перемещаем Z на элемент перед a.
- Выполняем обычные действия быстрой сортировки: выбор элемента для разделения и само разделение. Получаем три блока.
- Делаем блокофикацию третьего блока: ищем в нем максимальный элемент и перемещаем его в начало.
- Перемещаем Z на конец первого блока.
Теперь рассмотрим этот алгоритм на примере:

Где-то я уже видел этот массив… Давайте расставим указатели X, Y и Z:

Блок X-Z не отсортирован. Тогда найдем медиану:

Мы предполагаем, что процедура поиска медианы перемешивает элементы самым причудливым образом, оставляя саму медиану в самом начале (для наглядности примера! реализация может, например, возвращать итератор на элемент, который является медианой). Хорошо, давайте теперь выполним процедуру разделения:

Получились 3 блока. Блокофицируем последний блок и переместим Z в конец первого блока:

Теперь начинаем все с начала. Текущий блок X-Z не отсортирован, значит ищем в нем медиану:

Выполняем процедуру разделения:

Блокофицируем третий блок и перемещаем Z в конец первого блока:

Опять смотрим на X-Z:

Нам повезло! Блок отсортирован, поэтому его можно оставить в покое и искать следующий блок. Указатели X и Z переместятся следующим образом:

Внезапно, данный блок тоже отсортирован, поскольку это второй блок предыдущего шага. Ищем следующий блок:

Проверяем на упорядоченность — увы, на это раз не повезло, придется упорядочивать. Находим медиану, а потом делаем процедуру разделения:


Далее, мы перейдем к блоку [8,9], он отсортирован, поэтому X и Z сдвинутся на блок [10], который тоже отсортирован, после чего алгоритм будет рассматривать блок [13, 11, 12], в котором все уже совсем тривиально. Разбор сортировки второй половины массива предлагается выполнить читателю самостоятельно.
Код.
Приблизительный Median of Medians с O(1) дополнительной памяти
К сожалению, с Median of Medians такой фокус, как использование максимального элемента для идентификации блоков в flat quick sort, не пройдет, ибо элементы массива каждый раз перемешиваются непонятно каким образом. Здесь мы будем использовать другой фокус.
На самом деле, чтобы заставить quick sort работать за гарантированные O(nlogn), не обязательно находить точную медиану для этапа разделения. Достаточно найти что-то приблизительное. Если дать гарантию, что первый и третий блок после этапа разделения не будут превосходить Cn для некоторого конкретного С<1, quick sort будет работать за O(nlogn). Даже для C=0.99. С
Поэтому мы модифицируем Median of Medians так, чтобы он находил медиану с некоторой погрешностью K = O(log2n). То есть будет найден элемент, порядковый номер которого где-то в границах от n/2-K/2 до n/2+K/2. Поскольку K порядка степени логарифма, легко найдется такое (конкретное) n, начиная с которого отрезок [n/2-K/2, n/2+K/2] будет лежать, скажем, между 1/4n и 3/4n. Для всех меньших n сортировать можно просто пузырьком.
Почему K = O(log2n)? Да мы просто используем K элементов массива для того, чтобы хранить в них всю необходимую информацию по стеку (идея, опять же, товарища FordPerfect). Уровней рекурсии O(logn), на каждом из них нам нужно сохранить O(1) чисел на O(logn) бит. А медиану для quick sort найдем среди оставшихся N-K элементов.
Каждый бит представляется двумя последовательными различными элементами массива. Если первый из них меньше второго — бит хранит состояние 0, иначе — 1 (или наоборот). Первая задача, которую нам нужно решить — это найти K/2 пар различных элементов массива и понять что делать если столько пар не найдется.
Делается это очень просто. Пусть итераторы X и Y указывают на первый элемент массива. Будем двигать Y вперед пока не найдем элемент, не равный X. Если нашли — подвинем X вперед, поменяем местами элементы, на которые указывают X и Y, подвинем X еще раз вперед (+ еще надо обработать мелкий случай — подвинуть Y вперед, если он оказался перед X). И так пока не найдем K/2 пар. Что если Y уже дошел до конца массива, а K/2 пар еще не нашлись? Это означает, что все элементы от X до Y включительно одинаковые! (Довольно просто проверить, что этот инвариант сохраняется на протяжении выполнения всего алгоритма). Тогда в качестве опорного элемента можно сразу выбрать один из этих элементов. Если выбрать K < n/2, этот опорный элемент будет точной медианой.
Теперь вопрос: а не поломает ли работа со стеком асимптотику алгоритма? Это очень хороший вопрос, поскольку на первый взгляд кажется, что вершин в нашем рекурсивном дереве порядка O(n) и на каждую вершину нам надо O(log2n) операций со стеком. Неужели асимптотика ухудшается до O(nlog2n) для нашего Median of Medians (и до O(nlog3n) для всего алгоритма)? Тут все несколько сложнее.
Чтобы посчитать точное число вершин в дереве надо решить следующую рекурренту:
N(n) = N(n/5) + N(7N/10) + 1
N(n) = 1 для n<C
Что-то подобное можно было видеть выше, но замена Cn на 1 делает рекурренту несколько более сложной для вычисления. На помощь приходит метод Акра-Бацци. Наша рекуррента подходит всем условиям и после всех соответствующих подстановок получаем, что число вершин N(n) растет как O(n0.84) (Θ(n0.839780...) если быть более точным). Итого временная сложность алгоритма составляет O(n + n0.84log2n) = O(n).
Дальнейшее расписывание алгоритма я считаю излишним, нужно просто реализовать то, что было описано в одной из предыдущих глав статьи. Лучше сразу глянуть в код. Картинок тоже не будет — чтобы алгоритм вообще заработал, нужно довольно большое число элементов в массиве. Какое именно? Об этом чуть ниже.
Насколько непрактичен предложенный алгоритм? Вот некоторые выкладки:
Пусть мы хотим получить отклонение не более 1/4n от настоящей медианы (то есть K < n/2). Тогда нам надо забить стек на 3[logn] уровней рекурсии (тут log — двоичный, 3 из-за того, что (3/4)3 < 0.5, а [x] — это округление числа x вверх до ближайшего целого). На каждый уровень рекурсии нам надо 2[logn] бит — надо хранить текущую длину массива, какой по порядку элемент мы ищем сейчас (это число всегда укладывается в [logn]-1 бит) и еще один бит на поддержание порядка обхода дерева рекурсии (надо помнить из какой ветви рекурсии мы вернулись). На каждый бит 2 элемента, итого надо 12[logn]2 элементов под стек.
Теперь решаем уравнение: 12[logn]2 < n/2 или 24[logn]2 < n. Надо найти такое n', что для любого n>=n' 24[logn]2 < n. Такое n' порядка 3500. То есть для n<3500 надо сортировать пузырьком.
Предел для n, начиная с которого K всегда не превышает n — 1500, то есть для n<1500 сортировка даже не заработает (не хватит элементов для эмуляции стека), тут уже без раздумий надо пользоваться пузырьком. Впрочем, если поиграться константами, то, вероятно, можно эту оценку улучшить.
Код.
Код
Все ссылки на код по всей статье в одном месте:
- Quick sort + Median of Medians (Гарантированный O(nlogn), O(logn) доп. памяти)
- Flat quick sort + Median of Medians (Гарантированный O(nlogn), O(logn) доп. памяти)
- Flat quick sort + Approximate Median of Medians (Гарантированный O(nlogn), O(1) доп. памяти)
Почитать
- Обсуждение алгоритма на gamedev.ru.
- Median of Medians на википедии (en, ru).
- Про Quickselect можно почитать здесь и здесь.
- Метод Акра-Бацци на википедии.
- Manual Blum, Robert W. Floyd, Vaughan Pratt, Ronald L. Rivest, and Robert E. Tarjan. Time Bounds for Selection. (pdf, eng)
- S.Battiato, D.Cantone, D.Catalano and G.Cincotti. An Efficient Algorithm for the Approximate Median Selection Problem. (pdf, eng) — быстрый приблизительный вероятностный Median of Medians