
Современные компиляторы очень хорошо умеют оптимизировать код. Они удаляют никогда не выполняющиеся условные переходы, вычисляют константные выражения, избавляются от бессмысленных арифметических действий (умножение на 1, сложение с 0). Они оперируют данными, известными на момент компиляции.
В момент выполнения информации об обрабатываемых данных гораздо больше. На её основании можно выполнить дополнительные оптимизации и ускорить работу программы.
Оптимизированный для частного случая алгоритм всегда работает быстрее универсального (по крайней мере, не медленнее).
Что если для каждого набора входных данных генерировать оптимальный для обработки этих данных алгоритм?
Очевидно, часть времени выполнения уйдёт на оптимизацию, но если оптимизированный код выполняется часто, затраты окупятся с лихвой.
Как же технически это сделать? Довольно просто — в программу включается мини-компилятор, генерирующий необходимый код. Идея не нова, технология называется “компиляция времени исполнения” или JIT-компиляция. Ключевую роль JIT-компиляция играет в виртуальных машинах и интерпретаторах языков программирования. Часто используемые участки кода (или байт-кода) преобразуются в машинные команды, что позволяет сильно повысить производительность.
Java, Python, C#, JavaScript, Flash ActionScript — неполный (совсем неполный) список языков, в которых это используется. Я предлагаю решить конкретную задачу с использованием этой технологии и посмотреть, что получится.
Задача
Задачей возьмём реализацию интерпретатора математических выражений. На входе у нас строка вида
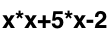
и число — значение x. На выходе должны получить число — значение выражения при этом значении x. Для простоты будем обрабатывать только четыре оператора — ‘+’, ‘-‘, ‘*’, ‘/’.
На данном этапе ещё не понятно, как вообще можно скомпилировать это выражение, ведь строка — не самый удобный для работы способ представления. Для анализа и вычислений лучше подойдёт дерево разбора, в нашем случае — бинарное дерево.
Для исходного выражения оно будет выглядеть так:
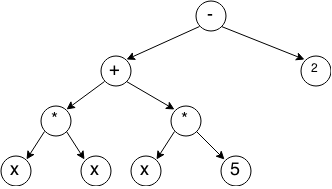
Каждый узел дерева представляет собой оператор, его дети — операнды. В листьях дерева оказываются константы и переменные.
Самым простым алгоритмом построения такого дерева является рекурсивный спуск — на каждом этапе мы находим оператор с наименьшим приоритетом, разбиваем выражение на две части — до этого оператора и после, и рекурсивно вызываем для этих частей операцию построения. Пошаговая иллюстрация работы алгоритма:
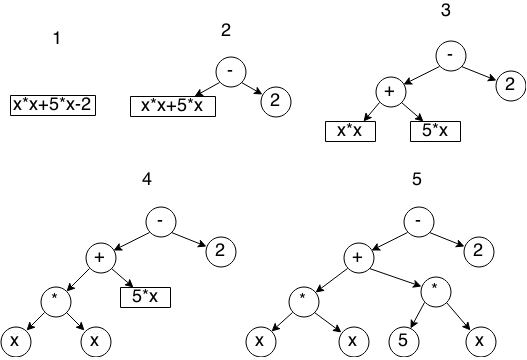
Реализацию алгоритма я тут приводить не буду по простой причине — он весьма объёмен, да и статья не про это.
Дерево состоит из узлов, каждый из которых будет представлен структурой TreeNode
typedef struct TreeNode TreeNode;
struct TreeNode
{
TreeNodeType type; //тип узла
TreeNode* left; //ссылка на левого потомка
TreeNode* right; //ссылка для правого потомка
float value; //значение (для узла-константы)
};
Вот все возможные типы узлов:
typedef enum
{
OperatorPlus, //Оператор плюс
OperatorMinus, //Оператор минус
OperatorMul, //Оператор умножить
OperatorDiv, //Оператор разделить
OperandConst, //Операнд - константа
OperandVar, //Операнд - переменная
OperandNegVar, //Операнд - переменная, взятая с минусом (для обработки унарного минуса)
} TreeNodeType;
Значение выражения при заданном x вычисляется очень просто — с помощью обхода в глубину.
Это тоже реализуется с помощью рекурсии.
float calcTreeFromRoot(TreeNode* root, float x)
{
if(root->type == OperandVar)
return x;
if(root->type == OperandNegVar)
return -x;
if(root->type == OperandConst)
return root->value;
switch(root->type)
{
case OperatorPlus:
return calcTreeFromRoot(root->left, x) + calcTreeFromRoot(root->right, x);
case OperatorMinus:
return calcTreeFromRoot(root->left, x) - calcTreeFromRoot(root->right, x);
case OperatorMul:
return calcTreeFromRoot(root->left, x) * calcTreeFromRoot(root->right, x);
case OperatorDiv:
return calcTreeFromRoot(root->left, x) / calcTreeFromRoot(root->right, x);
}
}
Что на текущий момент?
- Для выражения генерируется дерево
- При необходимости вычислить значение выражения вызывается рекурсивная функция calcTreeFromRoot
Как бы выглядел код, если бы мы знали выражение ещё на этапе сборки?
float calcExpression(float x)
{
return x * x + 5 * x - 2;
}
Вычисление значения выражения в таком случае сводится к вызову одной очень простой функции — в разы быстрее, чем рекурсивный обход дерева.
Время компиляции!
Хочу заметить, что я буду генерировать код для платформы x86 ориентируясь на процессоры архитектуры, схожей с IA32. Кроме того, я приму размер float равным 4 байтам, размер int равным 4 байтам.
Теория
Итак, наша задача получить обычную функцию языка C, которую можно будет вызывать при необходимости.
Для начала, определим её прототип:
typedef float _cdecl (*Func)(float);
Теперь тип данных Func представляет собой указатель на функцию, возвращающую значение типа float и принимающую один аргумент, тоже типа float.
_cdecl указывает на то, что используется соглашение о вызове C-declaration.
Это стандартное соглашение о вызове для языка C:
— аргументы передаются через стек справа на лево (при вызове на вершине стека должен оказаться первый аргумент)
— целочисленные значения возвращаются через регистр EAX
— значения с плавающей точкой возвращаются через регистр st0
— за сохранность регистров eax, edx, ecx отвечает вызывающая функция
— остальные регистры должна восстанавливать вызываемая функция
Вызов функции выглядит примерно так:
push ebp //Сохраняем указатель стекового фрейма
push arg3 //Кладём в стек аргументы в порядке справа на лево (первый аргумент в конце)
push arg2
push arg1
call func //Сам вызов
add esp, 0xC //Восстанавливаем указатель на стек (3 аргумента по 4 байта как раз займут 0xC байт)
pop ebp //Восстанавливаем указатель стекового фрейма
Состояние стека в момент вызова:
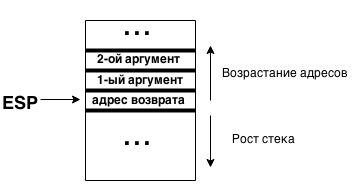
Как мы будем генерировать код, вычисляющий выражение? Время вспомнить, что есть такая штука как стековый калькулятор. Как он работает? На вход подаются числа и операторы. Алгоритм работы элементарен:
— Встретили константу или переменную — положили в стек
— Встретили оператор — сняли со стека 2 операнда, произвели операцию, положили результат в стек
Но кормить стековый калькулятор надо определённым образом — он работает с выражениями, представленными в обратной польской нотации. Её особенность заключается в том, что в записи сперва идут операнды, потом оператор. Таким образом наше исходное выражение предстанет в следующем виде:

Программа для стекового калькулятора соответствующая выражению:
push x
push x
mul
push 5
push x
mul
add
push 2
sub
Очень напоминает программу на ассемблере, не так ли?
Получается, достаточно перевести выражение в обратную польскую нотацию и создавать код следуя элементарным правилам.
Перевод выполнить очень просто — у нас уже есть построенное дерево разбора, надо только выполнить обход в глубину и при выходе из вершины генерировать соответствующее ей действие — получится последовательность команд в нужном нам порядке.
Псевдокод этого действа:
static void generateCodeR(TreeNode* root, ByteArray* code)
{
if(root->left && root->right)
{
generateCodeR(root->right, code); //Сначала должен сгенерироваться
generateCodeR(root->left, code); //код вычисления дочерних элементов
}
//Генерируем код для родительского элемента
if(root->type == OperandVar)
{
code += "push x"; //Кладём в стек значение аргумента (переменной)
}
else if(root->type == OperandNegVar)
{
code += "push -x"; //Кладём в стек значение аргумента со сменой знака
}
else if(root->type == OperandConst)
{
code += "push " + root->value; //Кладём в стек константу
}
else
{
code += "pop"; //Снимаем со стека
code += "pop"; //два значения
switch(root->type)
{
case OperatorPlus:
code += "add"; //Выполняем сложение
break;
case OperatorMinus:
code += "sub"; //Выполняем вычитание
break;
case OperatorMul:
code += "mul"; //Выполняем умножение
break;
case OperatorDiv:
code += "div"; //Выполняем деление
break;
}
code += "push result" //Сохраняем в стек результат математической операции
}
}
Реализация
Для начала определимся со стеком: с ним всё просто — регистр esp содержит указатель на вершину. Чтобы положить что-нибудь туда, достаточно выполнить команду
push {значение}
или вычесть из ESP число 4 и записать по полученному адресу нужное значение
sub esp, 4
mov [esp], {значение}
Снятие со стека выполняет команда pop или прибавление к esp число 4.
Раньше я упомянул соглашение о вызове. Благодаря ему мы можем точно знать, где будет находиться единственный аргумент функции. По адресу esp (на вершине) будет находиться адрес возврата, а по адресу esp — 4 как раз будет находиться значение аргумента. Так как обращение к нему будет происходить сравнительно часто можно поместить его в регистр eax:
mov eax, [esp - 4];
Теперь, немного про работу с числами с плавающей запятой. Мы будем использовать набор инструкций x87 FPU.
FPU имеет 8 регистров, образующих стек. Каждый из них вмещает 80 бит. Обращение к вершине этого стека происходит через регистр st0. Соответственно, регистр st1 адресует следующее за вершиной значение в этом стеке, st2 — следующее и так далее до st7.
Стек FPU:

Чтобы загрузить на вершину значение используется команда fld. Операндом этой команды может быть только хранящееся в памяти значение.
fld [esp] //Загрузить в st0 значение, хранящееся по адресу, содержащемуся в esp
Команды для выполнения арифметических операций очень просты: fadd, fsub, fmul, fdiv. У них может быть много разных комбинаций аргументов, но мы будем использовать их только так:
fadd dword ptr [esp]
fsub dword ptr [esp]
fmul dword ptr [esp]
fdiv dword ptr [esp]
Во всех этих случаях загружается значение из [esp], выполняется необходимая операция, результат сохраняется в st0.
Снять значение со стека тоже просто:
fstp [esp] //Удалить значение с верхушки FPU стека и сохранить его в ячейку памяти по адресу, лежащему в esp
Вспомним, что в выражении может встретиться переменная x с унарным минусом. Для её обработки надо сменить знак. Для этого гам пригодиться команда FCHS — она инвертирует бит знака регистра st0
Для каждой из этих команд определим по функции, генерирующей необходимые опкоды:
void genPUSH_imm32(ByteArray* code, int32_t* pValue);
void genADD_ESP_4(ByteArray* code);
void genMOV_EAX_PTR_ESP_4(ByteArray* code);
void genFSTP(ByteArray* code, void* dstAddress);
void genFLD_DWORD_PTR_ESP(ByteArray* code);
void genFADD_DWORD_PTR_ESP(ByteArray* code);
void genFSUB_DWORD_PTR_ESP(ByteArray* code);
void genFMUL_DWORD_PTR_ESP(ByteArray* code);
void genFCHS(ByteArray* code);
Чтобы код-вычислитель нормально отработал и вернул значение надо добавить перед ним и после него соответствующие инструкции. Всё это дело вместе собирает функция-обёртка generateCode:
void generateCode(Tree* tree, ByteArray* resultCode)
{
ByteArray* code = resultCode;
genMOV_EAX_ESP_4(code); //Помещаем в eax значение аргумента
generateCodeR(tree->root, code); //Генерируем код-вычислитель
genFLD_DWORD_PTR_ESP(code);
genADD_ESP_4(code); //Снимаем лишнее двойное слово со стека
genRET(code); //Выходим из функции
}
Конечный вид функции генерации кода, вычисляющего значение выражения:
void generateCodeR(TreeNode* root, ByteArray* resultCode)
{
ByteArray* code = resultCode;
if(root->left && root->right)
{
generateCodeR(root->right, code);
generateCodeR(root->left, code);
}
if(root->type == OperandVar)
{
genPUSH_EAX(code); //В eax лежт аргумент функции
}
else if(root->type == OperandNegVar)
{
genPUSH_EAX(code); //Загружаем в стек
genFLD_DWORD_PTR_ESP(code); //Меняем
genFCHS(code); //знак
genFSTP_DWORD_PTR_ESP(code);//Возвращаем в стек
}
else if(root->type == OperandConst)
{
genPUSH_imm32(code, (int32_t*)&root->value);
}
else
{
genFLD_DWORD_PTR_ESP(code);//Загружаем в FPU левый операнд..
genADD_ESP_4(code); //… и снимаем его со стека
switch(root->type)
{
case OperatorPlus:
genFADD_DWORD_PTR_ESP(code); //Выполняем сложение (результат сохраниться в st0)
break;
case OperatorMinus:
genFSUB_DWORD_PTR_ESP(code); //Выполняем вычитание (результат сохраниться в st0)
break;
case OperatorMul:
genFMUL_DWORD_PTR_ESP(code); //Выполняем умножение (результат сохраниться в st0)
break;
case OperatorDiv:
genFDIV_DWORD_PTR_ESP(code); //Выполняем деление (результат сохраниться в st0)
break;
}
genFSTP_DWORD_PTR_ESP(code);//Сохраняем результат в стек (st0 -> [esp])
}
}
Кстати, о буфере для хранения кода. Для этих целей я создал тип-контейнер ByteArray:
typedef struct
{
int size; //Размер выделенной памяти
int dataSize; //Фактический размер хранящихся данных
char* data; //Указатель на данные
} ByteArray;
ByteArray* byteArrayCreate(int initialSize);
void byteArrayFree(ByteArray* array);
void byteArrayAppendData(ByteArray* array, const char* data, int dataSize);
Он позволяет добавлять в конец данные и не задумываться о выделении памяти — эдакий динамический массив.
Если сгенерировать код с помощью generateCode() и передать ему управление, скорее всего программа рухнет. Причина проста — отсутствие разрешения на исполнение. Я пишу под Windows, поэтому мне тут поможет WinAPI функция VirtualProtect, позволяющая задать права для области памяти (вернее для страниц памяти).
В MSD она описана так:
BOOL WINAPI VirtualProtect(
_In_ LPVOID lpAddress, //Адрес начала региона в памяти
_In_ SIZE_T dwSize, //Размер региона в памяти
_In_ DWORD flNewProtect, //Новые параметры доступа для страниц в регионе
_Out_ PDWORD lpflOldProtect //Указатель на переменную, куда сохранить старые параметры доступа
);
Она используется в основной функции-компиляторе:
CompiledFunc compileTree(Tree* tree)
{
CompiledFunc result;
DWORD oldP;
ByteArray* code;
code = byteArrayCreate(2); //Начальный размер контейнера - 2 байта
generateCode(tree, code); //Генерируем код
VirtualProtect(code->data, code->dataSize, PAGE_EXECUTE_READWRITE, &oldP); //Даём права на исполнение
result.code = code;
result.run = (Func)result.code->data;
return result;
}
CompiledFunc — структура, для удобного хранения кода и указателя на функцию:
typedef struct
{
ByteArray* code; //Контейнер с кодом
Func run; //Указатель на функцию
} CompiledFunc;
Компилятор написан и использовать его очень просто:
Tree* tree;
CompiledFunc f;
float result;
tree = buildTreeForExpression("x+5");
f = compileTree(tree);
result = f.run(5); //result = 10
Осталось только провести тестирование на скорость.
Тестирование
При тестировании я буду сравнивать время работы скомпилированного кода и рекурсивного алгоритма вычисления на основе дерева. Замерять время будем с помощью функции clock() из стандартной библиотеки. Чтобы вычислить время работы участка кода достаточно сохранить результат её вызова до и после профилируемой части. Если найти разность этих значений поделить на константу CLOCKS_PER_SEC можно получить время работы кода в секундах. Конечно, это не очень точный способ замеров, но мне точнее и не требовалось.
Во избежание сильного влияния погрешностей будем замерять время многократного вызова функций.
Код для тестирования:
double measureTimeJIT(Tree* tree, int iters)
{
int i;
double result;
clock_t start, end;
CompiledFunc f;
start = clock();
f = compileTree(tree);
for (i = 0; i < iters; i++)
{
f.run((float) (i % 1000));
}
end = clock();
result = (end - start) / (double)CLOCKS_PER_SEC;
compiledFuncFree(f);
return result;
}
double measureTimeNormal(Tree* tree, int iters)
{
int i;
clock_t start, end;
double result;
start = clock();
for (i = 0; i < iters; i++)
{
calcTree(tree, (float) (i % 1000));
}
end = clock();
result = (end - start) / (double)CLOCKS_PER_SEC;
return result;
}
Код самого тестера можно посмотреть в репозитории. Всё что он делает — последовательно увеличивает размер входных данных в регулируемых пределах, вызывает указанные выше функции тестирования и записывает результаты в файл.
По этим данным я построил график зависимости времени исполнения от размера входных данных (длины выражения). В качестве числа итераций для замера я взял 1 миллион. Просто так. Длина строки последовательно возрастала от 0 до 2000.
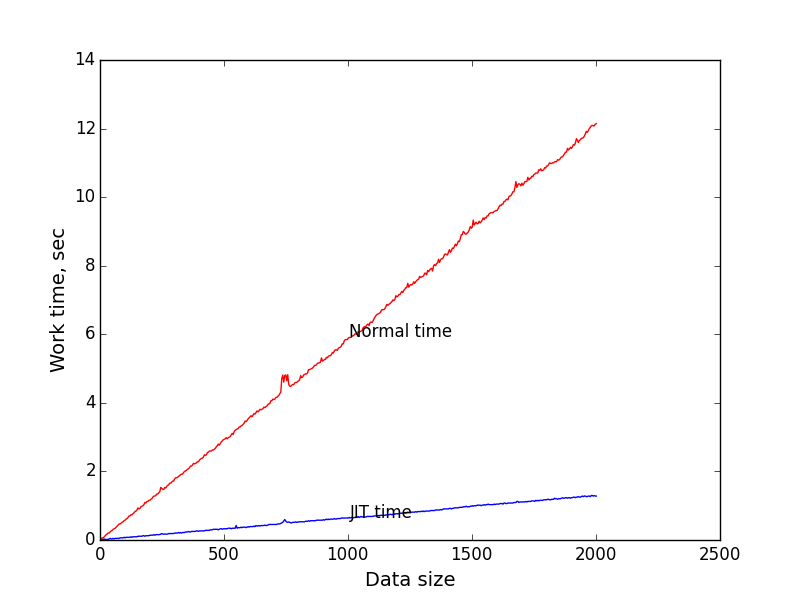
Синий график — зависимость времени исполнения компилированного кода от размера задачи.
Красный график — зависимость времени исполнения рекурсивного алгоритма от размера задачи.
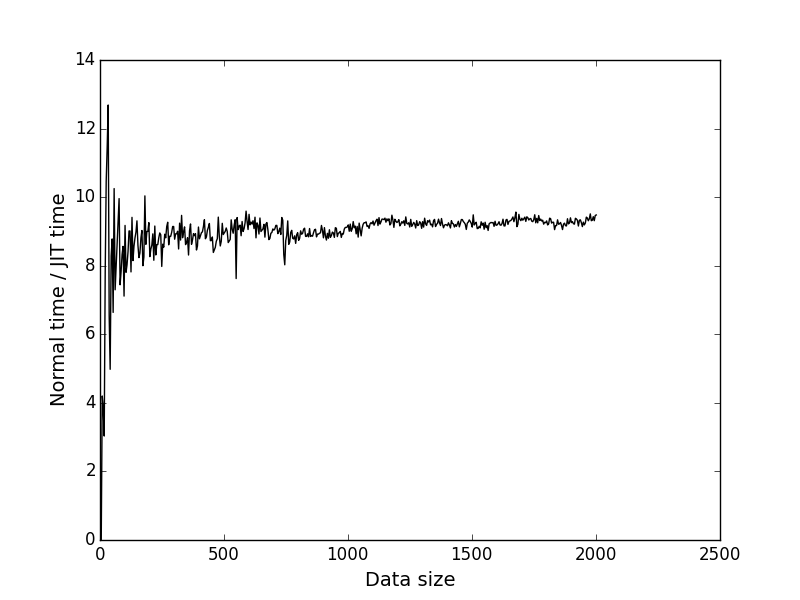
Чёрный график — отношение y координаты соответственных точек первого и второго графика. Показывает во сколько раз JIT быстрее в зависимости от размера задачи.
Видно, что при размере входных данных = 2000 JIT выигрывает примерно в 9.4 раза. Мне кажется это весьма неплохо.
Почему с JIT получается быстрее?
Скомпилированный код абсолютно линейный — ни одного условного перехода. Благодаря этому за время исполнения не происходит ни одного сброса конвейера процессора, что крайне благотворно влияет на производительность.
Что можно было сделать лучше?
Самой большой проблемой нашего компилятора является то, что он не использует все возможности FPU. В FPU 8 регистров, мы используем от силы два. Если бы удалось перенести часть нашего стека в стек FPU, уверен, скорость вычислений бы сильно увеличилась (кончено, это надо тестировать).
Ещё один недостаток — компилятор весьма глуп. Он не вычисляет константных выражений, не избегает лишних вычислений. Очень легко составить выражение так, чтобы он тратил максимум ресурсов. Если добавить элементарный упроститель выражений, компилятор станет близким к идеальному.
Проблемой самой реализации можно считать невозможность простого переноса на другую платформу (в функции генерации кода используются конкретные команды) и операционную систему (VirtualProtect, всё же). Вполне очевидным и довольно простым решением будет абстрагирование зависящих от платформы и ОС частей и вынесение их реализаций в отдельные модули.
Спасибо за прочтение, очень жду комментариев и советов.
Репозиторий: bitbucket.org/Informhunter/jithabr
На статью меня вдохновила книга “Совершенный код”, а именно, её глава “Динамическая генерация кода для обработки изображений”.