«Бог всегда на стороне больших батальонов» — Жак д'Эстамп дела Ферте, французский маршал
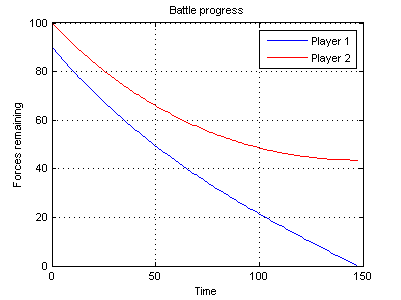 Рис. 1
Рис. 1
Во многих компьютерных играх необходимо симулировать сражения без отображения их хода на экране. Например, это может быть Rogue-like пошаговая игра, в которой компьютер должен посчитать только исход сражения (кто победил) и потери сторон. Даже в интерактивных играх сражения, которые происходят за пределами поля видимости игрока, можно моделировать упрощенно. Я разработал интересную математическую модель для такого моделирования и представляю ее читателям.
В статье рассматривается «непрерывный» подход — то есть силы сторон являются непрерывными величинами, а их взаимодействие происходит в непрерывном времени. Это позволяет воспользоваться методами мат. анализа и получить решение в явном виде. Для армий, состоящих из большого количества боевых единиц, такое упрощение не вносит большой погрешности. Вместе с тем, решение в явном виде позволяет понять многое о задаче.
Исходными данными для симуляции сражения обычно являются силы сторон — количество солдат или других боевых единиц. Встречаются случаи разнородных армий, состоящих из нескольких типов боевых единиц. Но мы пока оставим эти сложности в стороне и рассмотрим наиболее простой случай: встреча двух армий, состоящих из одинаковых солдат, в равных боевых условиях, и различающихся лишь количественно.
Поэтому исходными данными у нас будет два числа — количество солдат в каждой армии на момент начала сражения.
В реальных сражениях солдаты стреляют друг в друга или атакуют в ближнем бою. Каждый акт атаки является дискретным, атака может привести к поражению противника или пройти мимо. После совершения атаки солдат должен перезарядить или перенацелить ружье, или заново замахнуться мечом, т.е. так или иначе, он не сразу может совершить еще одну атаку. Результативность атак зависит от мощности оружия солдата, крепости брони противника, ловкости обоих и других факторов. Но все эти сложности без большого ущерба для точности моделирования можно заменить одним коэффициентом.
Пусть k — коэффициент, который определяет, сколько противников в среднем убивает каждый солдат за единицу времени. В этом коэффициенте можно учесть практически всё: улучшение оружия или меткости увеличивает k; броня и увертливость врага — уменьшают; также можно учесть влияние местности на поле боя, времени суток и т.д.
Редко бывает, что армии состоят из совершенно аналогичных солдат и встречаются в абсолютно равных условиях. «Оборона сильнее наступления» (Р. Клаузевиц). Поэтому коэффициент k для каждой армии будет различным. Но мы пока не будем усложнять и предположим, что коэффициент k у обеих армий одинаков, а позже обобщим результаты на случай различных коэффициентов.
Пусть x(t) — количество солдат первой армии, которое уменьшается по мере того, как их убивает противник. Пусть y(t) — количество солдат второй армии. Тогда описанную выше модель взаимодействия можно едва ли не буквально перевести на математический язык:

То есть: скорость убыли солдат первой армии пропорциональна количеству солдат во второй армии, и наоборот.
Получилась система дифференциальных уравнений. Она несложно решается, в частности, с помощью Wolfram Alpha. Общее решение:

Где C1 и C2 — константы интегрирования, которые необходимо найти исходя из начальных условий. Если количество солдат первой армии в момент начала сражения t=0 равно x0, а второй армии, соответственно, y0 — то подставим и получим C1=x0, C2=y0. После упрощения нужное нам частное решение окончательно выглядит так:
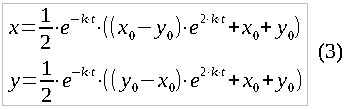
Итак, мы нашли функции, устанавливающие зависимость количества оставшихся солдат каждой из сторон от времени, проведенного в сражении. Пример графика таких функций приведен на рис. 1.
Какого поведения можно ожидать от полученных функций?
Подставим для примера x0=y0, т.е. смоделируем бой между равными армиями и посмотрим, что получится. Член с exp(2*k*t) уничтожается, и остается x(t) = y(t) = x0*exp(-k*t). Обе армии уничтожают друг друга по экспоненте, их численность убывает очень быстро, однако нуля никогда не достигает. Сражение будет длиться вечно, и бесконечно малое количество оставшихся солдат будет компенсироваться бесконечно малой скоростью их убыли.
Если же теперь подставить разные значения, например, x0=90 и y0=100 (как на рис. 1) — то член с exp(2*k*t) будет действовать для каждой армии по-разному. Та армия, которая исходно имела больше солдат, получит «добавку» от exp(2*k*t) в положительную сторону, то есть, скорость ее убыли замедлится. Другая же армия, более малочисленная, получит ту же «добавку» в минус, так что она будет редеть быстрее. В итоге за конечное время t1 численность более слабой армии достигнет нуля. Сражение закончится разгромом этой армии.
Снова посмотрим на рис. 1. Видно, что в начале графика обе функции убывают примерно одинаково, так как разница в численности армий небольшая. Но постепенно разница в скорости убыли нарастает, и это самоподдерживающийся эффект. Небольшое исходное численное преимущество (всего на 10%) не только обеспечивает победу в сражении, но почти половина солдат победившей армии выживает.
Результат тем более впечатляет, что график на рис. 1 был построен исходя из значения k=0.01. Представим себе, что время измеряется в минутах. Это означает, что каждую минуту солдат одной армии убивает в среднем 0.01 солдата противника. То есть, допустим, он стреляет каждую минуту один раз, и попадает с вероятностью 1%. Это весьма низкие скорострельность и вероятность попадания. Тем не менее, сражение заканчивается примерно за 150 минут полным уничтожением более слабой армии. Это все из-за того, что у нас в решениях экспоненты.
Вычисление x(t) и y(t) после того, как одна из этих функций достигла нуля (т.е. после победы одной из сторон) не имеет смысла. Так, в частности, при t>t1 x(t) станет меньше нуля, а y(t) начнет расти. Чтобы знать, до какого значения t вести расчеты, следует найти t1.
Найдем момент разгрома t1 для случая x0<y0. Подставим x(t1)=0 в формулу (3) и после преобразований получим:

Теперь можно привести Матлаб-код, который использует формулы (3) и (4) для построения графиков хода сражения.
Также представляет интерес найти потери победившей стороны. Подставляя найденное t1 из формулы (4) в формулу (3), после преобразований, получим:
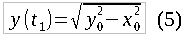
В принципе, формула (5) представляет собой основной результат данной статьи, так как и без того было понятно, что более многочисленная армия выигрывает, а если нас не интересует ход сражения, а только его результат — то необходимо найти лишь потери победившей стороны.
Любопытно, что потери победителя не зависят от k, а зависят только от первоначального соотношения сил. От k зависит только длительность сражения.
Попробуем выразить время сражения и потери победителя не через абсолютные величины x0 и y0, а через их отношение. Пусть r=x0/y0 (0<r<1 при x0<y0), тогда x0=r*y0 и после преобразований получаем:
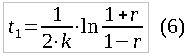
Потери победителя найдем как отношение количества солдат после сражения к количеству солдат до сражения:
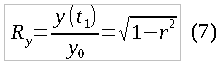
На рис. 2 приведен график функции Ry ( r ):
 Рис. 2
Рис. 2
Видно, что армия-победительница несет в общем малые потери, что подтверждает тезис о больших батальонах, вынесенный в эпиграф. Даже при соотношении сторон 10:9 выживает почти половина победившей армии, и только при r>0.95 у победителя наблюдаются существенные потери, что можно говорить о «пирровой победе».
Неравные условия боя (различия в подготовке солдат, вооружениях, броне, оборона против наступления, факторы местности) можно учесть, если в системе уравнений (1) ввести разные коэффициенты k1 и k2 вместо одного k. То есть средняя скорость истребления противника у солдат каждой из армий будет различаться:
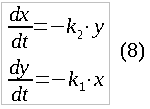
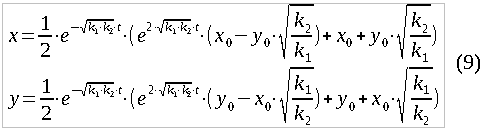
Нужное нам частное решение такой системы, аналогично формуле (3), выглядит так:
Выражения получились более громоздкими, но если ввести подстановку: p=sqrt(k1*k2), r=sqrt(k1/k2)*x0/y0 — то все существенно упрощается:

В принципе, если сделать аналогичную подстановку для системы (3) — то системы (3) и (10) будут выглядеть одинаково, и разница между ними будет заключаться только в выражении для r: для случая разных k1 и k2 в выражении для r появляется множитель вида sqrt(k1/k2).
Критерий победы теперь — сравнение r с 1. Если r>1 — то побеждает первая армия (x), если r<1 — то вторая (y). При r=1 обе армии взаимно уничтожаются за бесконечное время.
Время победы совпадает с формулой (6) с той лишь разницей, что вместо k теперь фигурирует p:

И наконец, оставшиеся солдаты победителя: формула (7) применима без изменений в случае использования новой подстановки для r.
Симуляция сражений в непрерывных функциях позволяет получить обоснованные результаты при минимуме вычислительных затрат. Даже в более сложном случае неравных условий боя, результат битвы может быть вычислен с помощью всего лишь трех вызовов квадратного корня и нескольких сложений, умножений и делений. Вычислительная сложность — O(1).
Преимущество «больших батальонов» очень наглядно следует из приведенных формул и графиков. Особенно впечатляет то, что даже малое численное преимущество приводит в модели к полному разгрому противника при гораздо меньших потерях, чем можно интуитивно ожидать.
Почему же исход реальных сражений так непредсказуем, в отличие от модели? Конечно, из-за влияния случайных факторов, которые неизвестны во время расчетов. В моей модели влияние случайностей где-то может быть отражено в коэффициентах k1 и k2. Эти коэффициенты определяющим образом влияют на исход сражения и могут перевесить чашу весов в ту или другую сторону.
Предложенный мной подход можно развивать в том направлении, чтобы применить к нему теорвер и мат. статистику. Также было бы интересно разработать модель для разнородных армий, состоящих из нескольких видов войск. Но это уже тема для отдельных исследований и новой статьи. Спасибо за внимание.
 Рис. 1
Рис. 1Во многих компьютерных играх необходимо симулировать сражения без отображения их хода на экране. Например, это может быть Rogue-like пошаговая игра, в которой компьютер должен посчитать только исход сражения (кто победил) и потери сторон. Даже в интерактивных играх сражения, которые происходят за пределами поля видимости игрока, можно моделировать упрощенно. Я разработал интересную математическую модель для такого моделирования и представляю ее читателям.
В статье рассматривается «непрерывный» подход — то есть силы сторон являются непрерывными величинами, а их взаимодействие происходит в непрерывном времени. Это позволяет воспользоваться методами мат. анализа и получить решение в явном виде. Для армий, состоящих из большого количества боевых единиц, такое упрощение не вносит большой погрешности. Вместе с тем, решение в явном виде позволяет понять многое о задаче.
Исходные данные
Исходными данными для симуляции сражения обычно являются силы сторон — количество солдат или других боевых единиц. Встречаются случаи разнородных армий, состоящих из нескольких типов боевых единиц. Но мы пока оставим эти сложности в стороне и рассмотрим наиболее простой случай: встреча двух армий, состоящих из одинаковых солдат, в равных боевых условиях, и различающихся лишь количественно.
Поэтому исходными данными у нас будет два числа — количество солдат в каждой армии на момент начала сражения.
Модель взаимодействия
В реальных сражениях солдаты стреляют друг в друга или атакуют в ближнем бою. Каждый акт атаки является дискретным, атака может привести к поражению противника или пройти мимо. После совершения атаки солдат должен перезарядить или перенацелить ружье, или заново замахнуться мечом, т.е. так или иначе, он не сразу может совершить еще одну атаку. Результативность атак зависит от мощности оружия солдата, крепости брони противника, ловкости обоих и других факторов. Но все эти сложности без большого ущерба для точности моделирования можно заменить одним коэффициентом.
Пусть k — коэффициент, который определяет, сколько противников в среднем убивает каждый солдат за единицу времени. В этом коэффициенте можно учесть практически всё: улучшение оружия или меткости увеличивает k; броня и увертливость врага — уменьшают; также можно учесть влияние местности на поле боя, времени суток и т.д.
Редко бывает, что армии состоят из совершенно аналогичных солдат и встречаются в абсолютно равных условиях. «Оборона сильнее наступления» (Р. Клаузевиц). Поэтому коэффициент k для каждой армии будет различным. Но мы пока не будем усложнять и предположим, что коэффициент k у обеих армий одинаков, а позже обобщим результаты на случай различных коэффициентов.
Основные уравнения и их решение
Пусть x(t) — количество солдат первой армии, которое уменьшается по мере того, как их убивает противник. Пусть y(t) — количество солдат второй армии. Тогда описанную выше модель взаимодействия можно едва ли не буквально перевести на математический язык:

То есть: скорость убыли солдат первой армии пропорциональна количеству солдат во второй армии, и наоборот.
Получилась система дифференциальных уравнений. Она несложно решается, в частности, с помощью Wolfram Alpha. Общее решение:

Где C1 и C2 — константы интегрирования, которые необходимо найти исходя из начальных условий. Если количество солдат первой армии в момент начала сражения t=0 равно x0, а второй армии, соответственно, y0 — то подставим и получим C1=x0, C2=y0. После упрощения нужное нам частное решение окончательно выглядит так:
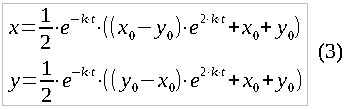
Итак, мы нашли функции, устанавливающие зависимость количества оставшихся солдат каждой из сторон от времени, проведенного в сражении. Пример графика таких функций приведен на рис. 1.
Анализ результатов
Какого поведения можно ожидать от полученных функций?
Подставим для примера x0=y0, т.е. смоделируем бой между равными армиями и посмотрим, что получится. Член с exp(2*k*t) уничтожается, и остается x(t) = y(t) = x0*exp(-k*t). Обе армии уничтожают друг друга по экспоненте, их численность убывает очень быстро, однако нуля никогда не достигает. Сражение будет длиться вечно, и бесконечно малое количество оставшихся солдат будет компенсироваться бесконечно малой скоростью их убыли.
Если же теперь подставить разные значения, например, x0=90 и y0=100 (как на рис. 1) — то член с exp(2*k*t) будет действовать для каждой армии по-разному. Та армия, которая исходно имела больше солдат, получит «добавку» от exp(2*k*t) в положительную сторону, то есть, скорость ее убыли замедлится. Другая же армия, более малочисленная, получит ту же «добавку» в минус, так что она будет редеть быстрее. В итоге за конечное время t1 численность более слабой армии достигнет нуля. Сражение закончится разгромом этой армии.
Снова посмотрим на рис. 1. Видно, что в начале графика обе функции убывают примерно одинаково, так как разница в численности армий небольшая. Но постепенно разница в скорости убыли нарастает, и это самоподдерживающийся эффект. Небольшое исходное численное преимущество (всего на 10%) не только обеспечивает победу в сражении, но почти половина солдат победившей армии выживает.
Результат тем более впечатляет, что график на рис. 1 был построен исходя из значения k=0.01. Представим себе, что время измеряется в минутах. Это означает, что каждую минуту солдат одной армии убивает в среднем 0.01 солдата противника. То есть, допустим, он стреляет каждую минуту один раз, и попадает с вероятностью 1%. Это весьма низкие скорострельность и вероятность попадания. Тем не менее, сражение заканчивается примерно за 150 минут полным уничтожением более слабой армии. Это все из-за того, что у нас в решениях экспоненты.
Вычисление x(t) и y(t) после того, как одна из этих функций достигла нуля (т.е. после победы одной из сторон) не имеет смысла. Так, в частности, при t>t1 x(t) станет меньше нуля, а y(t) начнет расти. Чтобы знать, до какого значения t вести расчеты, следует найти t1.
Вывод формул для времени победы t1 и потерь победившей армии
Найдем момент разгрома t1 для случая x0<y0. Подставим x(t1)=0 в формулу (3) и после преобразований получим:

Теперь можно привести Матлаб-код, который использует формулы (3) и (4) для построения графиков хода сражения.
Программа рисования графика для рис. 1
x0 = 90; % Number of soldiers in army-1
y0 = 100; % Number of soldiers in army-2
k = 0.01; % Damage to armor factor
%----------------------------------
if x0~=y0
t_end = log((x0+y0)./abs(x0-y0))./2./k;
else
t_end = 1000;
end
t = [0:floor(t_end) t_end];
x = 0.5*exp(-k*t).*((x0-y0)*exp(2*k*t)+x0+y0);
y = 0.5*exp(-k*t).*((y0-x0)*exp(2*k*t)+x0+y0);
figure(1);
plot(t,x);
hold on
plot(t,y,'r');
hold off
grid on
ylim([0 max(x0,y0)]);
xlabel('Time')
ylabel('Forces remaining')
legend({'Player 1','Player 2'})
title('Battle progress')
Также представляет интерес найти потери победившей стороны. Подставляя найденное t1 из формулы (4) в формулу (3), после преобразований, получим:
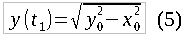
В принципе, формула (5) представляет собой основной результат данной статьи, так как и без того было понятно, что более многочисленная армия выигрывает, а если нас не интересует ход сражения, а только его результат — то необходимо найти лишь потери победившей стороны.
Любопытно, что потери победителя не зависят от k, а зависят только от первоначального соотношения сил. От k зависит только длительность сражения.
Попробуем выразить время сражения и потери победителя не через абсолютные величины x0 и y0, а через их отношение. Пусть r=x0/y0 (0<r<1 при x0<y0), тогда x0=r*y0 и после преобразований получаем:
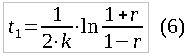
Потери победителя найдем как отношение количества солдат после сражения к количеству солдат до сражения:
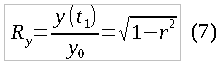
На рис. 2 приведен график функции Ry ( r ):
 Рис. 2
Рис. 2Видно, что армия-победительница несет в общем малые потери, что подтверждает тезис о больших батальонах, вынесенный в эпиграф. Даже при соотношении сторон 10:9 выживает почти половина победившей армии, и только при r>0.95 у победителя наблюдаются существенные потери, что можно говорить о «пирровой победе».
Обобщение на случай неравных условий боя
Неравные условия боя (различия в подготовке солдат, вооружениях, броне, оборона против наступления, факторы местности) можно учесть, если в системе уравнений (1) ввести разные коэффициенты k1 и k2 вместо одного k. То есть средняя скорость истребления противника у солдат каждой из армий будет различаться:
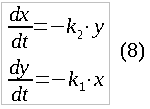
Нужное нам частное решение такой системы, аналогично формуле (3), выглядит так:

Выражения получились более громоздкими, но если ввести подстановку: p=sqrt(k1*k2), r=sqrt(k1/k2)*x0/y0 — то все существенно упрощается:

В принципе, если сделать аналогичную подстановку для системы (3) — то системы (3) и (10) будут выглядеть одинаково, и разница между ними будет заключаться только в выражении для r: для случая разных k1 и k2 в выражении для r появляется множитель вида sqrt(k1/k2).
Критерий победы теперь — сравнение r с 1. Если r>1 — то побеждает первая армия (x), если r<1 — то вторая (y). При r=1 обе армии взаимно уничтожаются за бесконечное время.
Время победы совпадает с формулой (6) с той лишь разницей, что вместо k теперь фигурирует p:

И наконец, оставшиеся солдаты победителя: формула (7) применима без изменений в случае использования новой подстановки для r.
Заключение
Симуляция сражений в непрерывных функциях позволяет получить обоснованные результаты при минимуме вычислительных затрат. Даже в более сложном случае неравных условий боя, результат битвы может быть вычислен с помощью всего лишь трех вызовов квадратного корня и нескольких сложений, умножений и делений. Вычислительная сложность — O(1).
Преимущество «больших батальонов» очень наглядно следует из приведенных формул и графиков. Особенно впечатляет то, что даже малое численное преимущество приводит в модели к полному разгрому противника при гораздо меньших потерях, чем можно интуитивно ожидать.
Почему же исход реальных сражений так непредсказуем, в отличие от модели? Конечно, из-за влияния случайных факторов, которые неизвестны во время расчетов. В моей модели влияние случайностей где-то может быть отражено в коэффициентах k1 и k2. Эти коэффициенты определяющим образом влияют на исход сражения и могут перевесить чашу весов в ту или другую сторону.
Предложенный мной подход можно развивать в том направлении, чтобы применить к нему теорвер и мат. статистику. Также было бы интересно разработать модель для разнородных армий, состоящих из нескольких видов войск. Но это уже тема для отдельных исследований и новой статьи. Спасибо за внимание.