Всем привет! Со школы, решая квадратичные уравнения ( КУ ), например  , получал корни обладающие мнимой составляющей,
, получал корни обладающие мнимой составляющей,  , и при желании увидеть как график пересекает ось
, и при желании увидеть как график пересекает ось  в точках
в точках  , в интернете находил графики вроде:
, в интернете находил графики вроде:
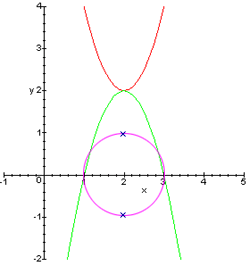
Как график с мнимой частью выглядит ( по моим размышлениям ) в 3D ( ), и есть тема данной статьи.
), и есть тема данной статьи.
PS: Под катом тяжёлые анимации
Как обычно, график ф-кции состоит из точек, а точки строятся по пересечению осей и
и  .
.
График ф-ции с комплексной составляющей ,
,
где
 — вектор
— вектор
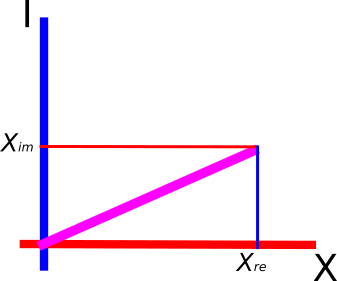
 — вектор
— вектор
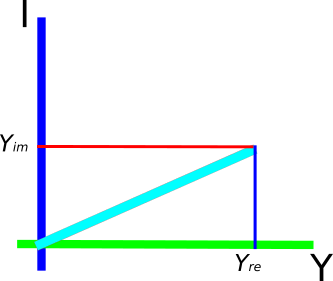
 можно представить в виде 3-х мерного вектора
можно представить в виде 3-х мерного вектора 
![$[X_{re}] - ось X$](https://habrastorage.org/getpro/habr/post_images/7e8/026/0d5/7e80260d5aa7e3cc91883e979ad689bd.svg)
![$[0] - ось Y$](https://habrastorage.org/getpro/habr/post_images/261/7d2/2c1/2617d22c113f6e0c664f5b35c5e20faa.svg)
![$[X_{im}] - ось I$](https://habrastorage.org/getpro/habr/post_images/277/abe/50d/277abe50de255d33946987066162145c.svg)
Аналогично
![$[0] - ось X$](https://habrastorage.org/getpro/habr/post_images/db1/387/ffc/db1387ffc5978747341f2da3e74c991a.svg)
![$[Y_{re}] - ось Y$](https://habrastorage.org/getpro/habr/post_images/d11/5d8/9b5/d115d89b5c56d1461e517aba14d69071.svg)
![$[Y_{im}] - ось I$](https://habrastorage.org/getpro/habr/post_images/407/595/f3a/407595f3a7064965c4a714c0fe115d8a.svg)
Точка пересечения и
и  будет равна сумме векторов
будет равна сумме векторов  и
и 
 +
+ =
=
С пересечением разобрался.
Далее для построения графика нужно определиться с изменением и
и  вдоль оси
вдоль оси  , для этого нужен корень КУ. Есть два варианта:
, для этого нужен корень КУ. Есть два варианта:
Я выбрал второй вариант. Возьмём, для примера:

Корни КУ




Когда
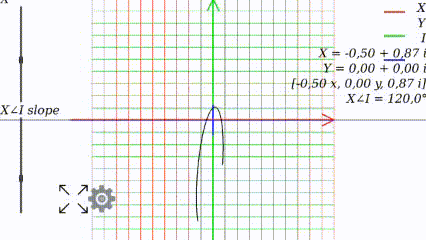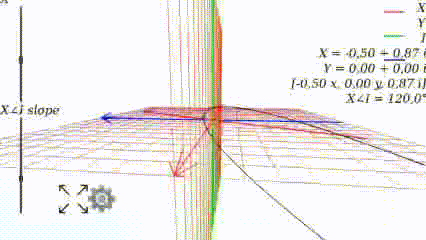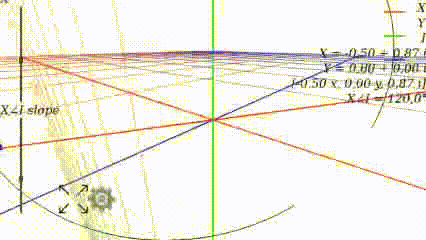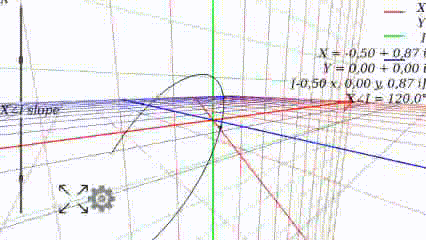
Когда угол равен 0, то график выглядит как привычно выглядел в школе:
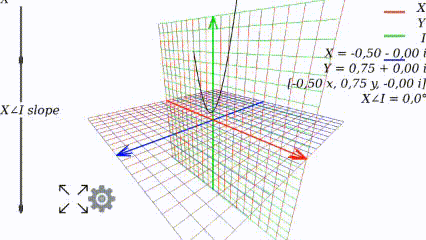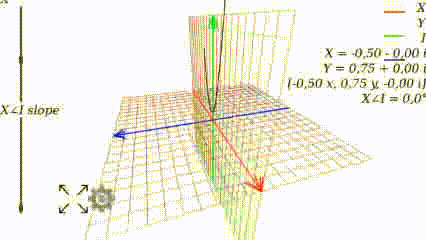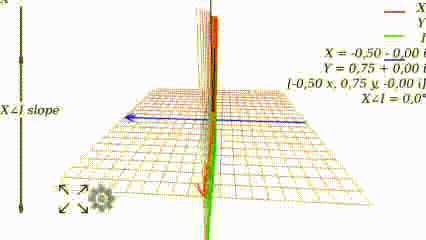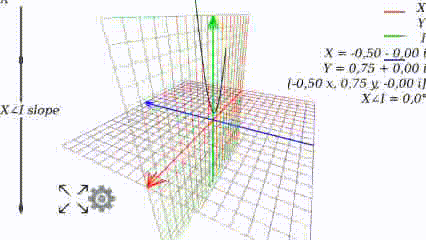
Меняя угол, видим как меняется график:

PS: Представленные графики и их анимации были созданы в приложении «Quadratic Complex 3D Graph» из Google Apps.

Как график с мнимой частью выглядит ( по моим размышлениям ) в 3D (
PS: Под катом тяжёлые анимации
Как обычно, график ф-кции состоит из точек, а точки строятся по пересечению осей
График ф-ции с комплексной составляющей
где


Аналогично
Точка пересечения
С пересечением разобрался.
Далее для построения графика нужно определиться с изменением
- Сделать
константой и изменять только
из корня КУ;
- Получить угол между
и
из корня КУ и перемещаться вдоль
, наращивая
,
вычислять с учётом угла и
.
Я выбрал второй вариант. Возьмём, для примера:
Корни КУ
Когда

Когда угол равен 0, то график выглядит как привычно выглядел в школе:

Меняя угол, видим как меняется график:

PS: Представленные графики и их анимации были созданы в приложении «Quadratic Complex 3D Graph» из Google Apps.