Привет, Хабр! Представляю вашему вниманию перевод статей блога ZCash, в которых рассказывается о механизме работы системы доказательств с нулевым разглашением SNARKs, применяемых в криптовалюте ZCash (и не только).
Источник
Предыдущие статьи:
Часть 1: Объяснение SNARKs. Гомоморфное скрытие и слепое вычисление полиномов (перевод)
Часть 2: Объяснение SNARKs. Знание о принятом коэффициенте и достоверное слепое вычисление полиномов (перевод)
Часть 3: Объяснение SNARKs. От вычислений к многочленам, протокол Пиноккио и спаривание эллиптических кривых (перевод)
В предыдущей статье был рассмотрен протокол Пиноккио для zk-SNARK. Осталось разобрать две вещи: Гомоморфное скрытие (ГС), которое поддерживает как добавление, так и умножение, необходимые для верификации, и переход от интерактивного протокола к неинтерактивной системе доказательств.
В этой статье будет показано, как с помощью эллиптических кривых можно получить ограниченную, но достаточную для наших целей форму ГС, которая поддерживает умножение. Далее будет показано, что этой ограниченной формы ГС также достаточно, чтобы преобразовать протокол в необходимую неинтерактивную систему.
Начнем с введения в эллиптические кривые и объяснения того, как они позволяют получить необходимую нам форму ГС.
Предположим, что p является простым числом больше 3, и возьмем некоторые такие, что
такие, что  . Рассмотрим уравнение:
. Рассмотрим уравнение:

Эллиптическая кривая C является множеством точек , которые удовлетворяют данному уравнению. Эти кривые дают нам интересный способ построения групп. Элементами группы будут точки
, которые удовлетворяют данному уравнению. Эти кривые дают нам интересный способ построения групп. Элементами группы будут точки  которые находятся на кривой, т. е. удовлетворяют уравнению вместе со специальной точкой O, нужная по техническим причинам иногда упоминается как «точка в бесконечности» и служит элементом идентичности, то есть нулем группы.
которые находятся на кривой, т. е. удовлетворяют уравнению вместе со специальной точкой O, нужная по техническим причинам иногда упоминается как «точка в бесконечности» и служит элементом идентичности, то есть нулем группы.
Теперь вопрос заключается в том, как сложить две точки чтобы получить третью? Правило сложения получается из некоторого абстрактного объекта, называемого группой классов дивизоров кривой. Для наших целей все, что вам нужно знать об этой группе классов дивизоров, состоит в том, что она накладывает следующее ограничение на определение операции сложения: сумма точек на любой линии должна быть равна нулю, т.е. O.
чтобы получить третью? Правило сложения получается из некоторого абстрактного объекта, называемого группой классов дивизоров кривой. Для наших целей все, что вам нужно знать об этой группе классов дивизоров, состоит в том, что она накладывает следующее ограничение на определение операции сложения: сумма точек на любой линии должна быть равна нулю, т.е. O.
Давайте рассмотрим, какое правило сложения вытекает из данного ограничения. Посмотрите на вертикальную линию, определяемую уравнением вида . Предположим, что эта линия пересекает кривую в точке
. Предположим, что эта линия пересекает кривую в точке  . Поскольку уравнение кривой имеет вид
. Поскольку уравнение кривой имеет вид  , если
, если  находится на кривой, то существует точка
находится на кривой, то существует точка  . Более того, поскольку это вертикальная линия, и уравнение кривой второго порядка Y, мы можем быть уверены, что это единственные точки, где пересекаются линия и кривая.
. Более того, поскольку это вертикальная линия, и уравнение кривой второго порядка Y, мы можем быть уверены, что это единственные точки, где пересекаются линия и кривая.
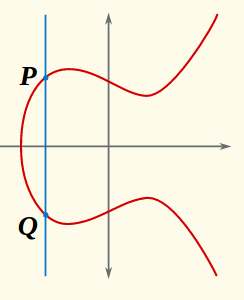
Таким образом, мы имеем уравнение , что означает
, что означает  Таким образом
Таким образом  является обратным к
является обратным к  в группе.
в группе.
Теперь давайте разберем точки $inlineP$inline и $inlineQ$inline, у которых не совпадают первые координаты, т.е. , и посмотрим, как их сложить. Проводим линию через P и Q.
, и посмотрим, как их сложить. Проводим линию через P и Q.
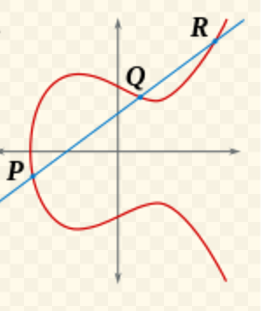
Так как кривая определяется полиномом третьей степени X и уже пересекает эту (не вертикальную) линию в двух точках, она гарантированно пересечет линию в третьей точке, которую мы обозначим , и не пересекает линию в других точках.
, и не пересекает линию в других точках.
Поэтому получаем , что означает
, что означает  . Мы уже знаем, что
. Мы уже знаем, что  получается из
получается из  с помощью разворота второй координаты из
с помощью разворота второй координаты из  в
в  .
.
Таким образом, правило сложения для нашей группы выглядит следующим образом: Для выбранных точек P и Q, необходимо провести через них линию, а затем взять «зеркальную» точку для третьей точки пересечения линии. Это и будет результатом сложения.
Эта группа обычно называется , поскольку она состоит из точек на кривой $inlineC$inline с координатами в
, поскольку она состоит из точек на кривой $inlineC$inline с координатами в  . Но будем обозначать ее далее как
. Но будем обозначать ее далее как  . Для удобства будем считать, что число элементов в
. Для удобства будем считать, что число элементов в  — простое число r, отличное от p. Это применяется во многих решениях, например, на кривой, которую использует Zcash. В этом случае любой элемент
— простое число r, отличное от p. Это применяется во многих решениях, например, на кривой, которую использует Zcash. В этом случае любой элемент  , отличающийся от O, генерирует
, отличающийся от O, генерирует  .
.
Наименьшее целое число k такое, что r делит называется степенью вложенности кривой. Считается, что если k достаточно большое, например, не менее 6, то задача дискретного логарифмирования в
называется степенью вложенности кривой. Считается, что если k достаточно большое, например, не менее 6, то задача дискретного логарифмирования в  , т.е. нахождение
, т.е. нахождение  и
и  из
из  , является достаточно сложной. (В кривых BN, используемых в настоящее время в Zcash,
, является достаточно сложной. (В кривых BN, используемых в настоящее время в Zcash,  ).
).
Мультипликативная группа содержит подгруппу порядка r которая обозначается
содержит подгруппу порядка r которая обозначается  . Мы можем посмотреть точки кривой с координатами в
. Мы можем посмотреть точки кривой с координатами в  и не только в
и не только в  . В соответствии с тем же правилом сложения, эти точки также образуют группу вместе с O, которая называется
. В соответствии с тем же правилом сложения, эти точки также образуют группу вместе с O, которая называется  . Заметим, что
. Заметим, что  явно содержит
явно содержит  . Помимо
. Помимо  будет содержать дополнительную подгруппу
будет содержать дополнительную подгруппу  порядка r(в действительности,
порядка r(в действительности,  дополнительных подгрупп порядка r).
дополнительных подгрупп порядка r).
Зафиксируем генераторы . Оказывается, существует эффективная карта, называемая упрощенным спариванием Тейта (Tate reduced pairing), переводящая пару элементов из
. Оказывается, существует эффективная карта, называемая упрощенным спариванием Тейта (Tate reduced pairing), переводящая пару элементов из  и
и  в элемент из
в элемент из  такой, что
такой, что
Определение Tate немного выходит за рамки серии этих статей и опирается на концепции из алгебраической геометрии, в большей степени на дивизоры.
Для многочлен
многочлен  принимает значение ноль в степени
принимает значение ноль в степени  в точке a, и нигде больше. Для точки
в точке a, и нигде больше. Для точки  , дивизоры позволяют доказать, что существует функция
, дивизоры позволяют доказать, что существует функция  от кривой на
от кривой на  , которая также принимает в некотором точном смысле ноль в степени r для P и нигде больше.
, которая также принимает в некотором точном смысле ноль в степени r для P и нигде больше.  тогда определяется как
тогда определяется как  .
.
Здесь может быть не до конца понятным, как это определение связано с указанными свойствами. В действительности же доказательство того, что Tate связано с этими свойствами достаточно сложное.
Определив мы получаем слабую версию ГС, которая поддерживает как сложение, так и умножение:
мы получаем слабую версию ГС, которая поддерживает как сложение, так и умножение:  являются ГС, которые поддерживают сложение, и зная скрытия
являются ГС, которые поддерживают сложение, и зная скрытия  мы можем вычислить
мы можем вычислить  . Другими словами, если у нас есть «правильные» скрытия x и y, мы можем получить (другое) скрытие xy. Но, например, если у нас есть скрытия для
. Другими словами, если у нас есть «правильные» скрытия x и y, мы можем получить (другое) скрытие xy. Но, например, если у нас есть скрытия для  , мы не сможем получить скрытие
, мы не сможем получить скрытие  .
.
Давайте перейдем к обсуждению неинтерактивных систем доказательств. Начнем с объяснения того, что мы подразумеваем под «неинтерактивным».
Самым сильным и интуитивно понятным определением неинтерактивного доказательства, вероятно, является следующее: Чтобы доказать определенное утверждение, доказывающая сторона передает единое сообщение доступное всем сторонам без какого-либо предварительного обмена сообщениями, и любой, кто прочитает это сообщение, будет убежден в верности утверждения. В большинстве случаев это может оказаться невозможным для реализации.
Ослабим определение неинтерактивного доказательства, чтобы внести понятие общей ссылающейся строки — ОСС (от англ. CRS). В модели ОСС, прежде чем будут построены какие-либо доказательства, существует фаза установки, в которой строка создается в соответствии с определенным случайным процессом и передается всем сторонам. Эта строка называется ОСС, а затем используется для создания и проверки доказательств. Предполагается, что случайные данные, используемые при создании ОСС, неизвестны ни одной из сторон, поскольку знание этих данных позволит построить ложные доказательства.
Давайте рассмотрим, как в модели ОСС можно преобразовать протокол достоверного слепого вычисления в неинтерактивную систему доказательств. Поскольку данный протокол состоит из нескольких похожих под-протоколов, он может быть превращен в неинтерактивную систему доказательств аналогичным образом.
Неинтерактивная версия протокола вычисления изначально состоит в публикации первого сообщения Боба как ОСС. Напомним, что целью протокола является получение гомоморфного скрытия для многочлена Алисы
для многочлена Алисы  для случайно выбранного
для случайно выбранного  .
.
Установка: Выбираются случайные и публикуется ОСС:
и публикуется ОСС:  .
.
Доказательство. Алиса вычисляет и
и  используя элементы ОСС, и тот факт, что
используя элементы ОСС, и тот факт, что  и
и  поддерживают линейные комбинации.
поддерживают линейные комбинации.
Проверка: Приняв для
для  и
и  , Боб вычисляет
, Боб вычисляет  и
и  , и проверяет их равенство. (Если они равны, то это значит, что
, и проверяет их равенство. (Если они равны, то это значит, что  .)
.)
Как было показано в предыдущих частях, Алиса может создать только такие , которые будут проходить проверки, если
, которые будут проходить проверки, если  является скрытием
является скрытием  для многочлена
для многочлена  порядка d, известного ей. Основное различие здесь в том, что Бобу не нужно знать
порядка d, известного ей. Основное различие здесь в том, что Бобу не нужно знать  для проверки, поскольку он может использовать функцию спаривание для вычисления
для проверки, поскольку он может использовать функцию спаривание для вычисления  только от
только от  и
и  . Следовательно, ему не нужно самостоятельно создавать и отправлять первое сообщение, и это сообщение может быть просто исправлено в ОСС.
. Следовательно, ему не нужно самостоятельно создавать и отправлять первое сообщение, и это сообщение может быть просто исправлено в ОСС.
Источник
Предыдущие статьи:
Часть 1: Объяснение SNARKs. Гомоморфное скрытие и слепое вычисление полиномов (перевод)
Часть 2: Объяснение SNARKs. Знание о принятом коэффициенте и достоверное слепое вычисление полиномов (перевод)
Часть 3: Объяснение SNARKs. От вычислений к многочленам, протокол Пиноккио и спаривание эллиптических кривых (перевод)
В предыдущей статье был рассмотрен протокол Пиноккио для zk-SNARK. Осталось разобрать две вещи: Гомоморфное скрытие (ГС), которое поддерживает как добавление, так и умножение, необходимые для верификации, и переход от интерактивного протокола к неинтерактивной системе доказательств.
В этой статье будет показано, как с помощью эллиптических кривых можно получить ограниченную, но достаточную для наших целей форму ГС, которая поддерживает умножение. Далее будет показано, что этой ограниченной формы ГС также достаточно, чтобы преобразовать протокол в необходимую неинтерактивную систему.
Начнем с введения в эллиптические кривые и объяснения того, как они позволяют получить необходимую нам форму ГС.
Эллиптические кривые и их спаривание
Предположим, что p является простым числом больше 3, и возьмем некоторые
Эллиптическая кривая C является множеством точек
Вы можете спросить «Набор точек на чем?». Мы имеем в виду множество точек с координатами в алгебраическом замыкании. Кроме того, кривая имеет аффинную и проективную версию. Когда ссылаемся на проективную версию, мы также включаем «точку на бесконечности» O как элемент кривой.
Теперь вопрос заключается в том, как сложить две точки
Давайте рассмотрим, какое правило сложения вытекает из данного ограничения. Посмотрите на вертикальную линию, определяемую уравнением вида

Таким образом, мы имеем уравнение
Теперь давайте разберем точки $inlineP$inline и $inlineQ$inline, у которых не совпадают первые координаты, т.е.

Так как кривая определяется полиномом третьей степени X и уже пересекает эту (не вертикальную) линию в двух точках, она гарантированно пересечет линию в третьей точке, которую мы обозначим
Поэтому получаем
Таким образом, правило сложения для нашей группы выглядит следующим образом: Для выбранных точек P и Q, необходимо провести через них линию, а затем взять «зеркальную» точку для третьей точки пересечения линии. Это и будет результатом сложения.
Мы не рассматривали случай сложения P с самим собой. Это делается с использованием линии, являющейся касательной к кривой в точке P, и получением R, как второй точки пересечения этой линии с кривой.
Эта группа обычно называется
Наименьшее целое число k такое, что r делит
Мультипликативная группа
Зафиксируем генераторы
для генератора ξ из
- Для заданной пары элементов
выполняется
Определение Tate немного выходит за рамки серии этих статей и опирается на концепции из алгебраической геометрии, в большей степени на дивизоры.
Фактически, спаривание Zcash использует оптимальное спариваниеAte, которое основано на упрощенном спаривание Тейта и может быть вычислено более эффективно, чем Tate.
Для
Здесь может быть не до конца понятным, как это определение связано с указанными свойствами. В действительности же доказательство того, что Tate связано с этими свойствами достаточно сложное.
Определив
Давайте перейдем к обсуждению неинтерактивных систем доказательств. Начнем с объяснения того, что мы подразумеваем под «неинтерактивным».
Неинтерактивные доказательства в модели общей ссылающейся строки
Самым сильным и интуитивно понятным определением неинтерактивного доказательства, вероятно, является следующее: Чтобы доказать определенное утверждение, доказывающая сторона передает единое сообщение доступное всем сторонам без какого-либо предварительного обмена сообщениями, и любой, кто прочитает это сообщение, будет убежден в верности утверждения. В большинстве случаев это может оказаться невозможным для реализации.
В терминах теории сложности вычислений можно показать, что только языки классов сложности BPP реализуют неинтерактивные доказательства с нулевым разглашением в полной мере. Тип утверждений, которые нам нужно доказать в транзакциях Zcash, например «Я знаю оригинал для хэша этой строки», соответствует классу сложности NP, который, как известно, намного больше, чем BPP.
Ослабим определение неинтерактивного доказательства, чтобы внести понятие общей ссылающейся строки — ОСС (от англ. CRS). В модели ОСС, прежде чем будут построены какие-либо доказательства, существует фаза установки, в которой строка создается в соответствии с определенным случайным процессом и передается всем сторонам. Эта строка называется ОСС, а затем используется для создания и проверки доказательств. Предполагается, что случайные данные, используемые при создании ОСС, неизвестны ни одной из сторон, поскольку знание этих данных позволит построить ложные доказательства.
Давайте рассмотрим, как в модели ОСС можно преобразовать протокол достоверного слепого вычисления в неинтерактивную систему доказательств. Поскольку данный протокол состоит из нескольких похожих под-протоколов, он может быть превращен в неинтерактивную систему доказательств аналогичным образом.
Неинтерактивный протокол вычисления
Неинтерактивная версия протокола вычисления изначально состоит в публикации первого сообщения Боба как ОСС. Напомним, что целью протокола является получение гомоморфного скрытия
Установка: Выбираются случайные
Доказательство. Алиса вычисляет
Проверка: Приняв
Как было показано в предыдущих частях, Алиса может создать только такие
Используемые изображения были взяты из данной статьи и используются по лицензии Creative Commons .