Привет, Хабр! Представляю вашему вниманию перевод моей статьи "Understanding the Customer Lifetime Value with Data Science".
Взаимоотношения с клиентами важны для каждой компании и играют ключевую роль в росте бизнеса. Одна из наиболее важных метрик в этой сфере — пожизненная ценность клиента (customer lifetime value, далее LTV) — предсказание чистого дохода, связанного со всеми будущими отношениями с клиентом. Чем дольше клиенты продолжают пользоваться продуктами компании, увеличивая прибыль, тем выше их LTV.
Есть много маркетинговых статей, о том, как важны LTV и сегментирование клиентов. Но, как Data Scientist’а, меня больше интересуют формулы и я хочу понимать, как модель на самом деле работает. Как предсказать LTV, используя только 3 признака? В этом посте я покажу некоторые модели, которые используются для маркетинговой сегментации клиентов и объясню математику, на которой они основаны. Здесь будет много формул, но не переживайте: все уже готово в библиотеках Python. Цель этого блога показать, как математика делает всю работу.
Beta-geometric/negative binomial модель для определения вероятности, что клиент “жив”
Рассмотрим такой пример [из онлайн-сервиса для заказа поездок (такси) по городу]: пользователь зарегистрировался 1 месяц назад, сделал 4 поездки и последняя поездка состоялась 20 дней назад. Основываясь только на этих данных, эта модель может предсказать вероятность, что клиент будет активен в течение определенного периода времени (как показано на графике), а также число транзакций в будущем (которое является основой для понимания ценности клиента в течение всей его “жизни” — взаимоотношений клиента и компании).
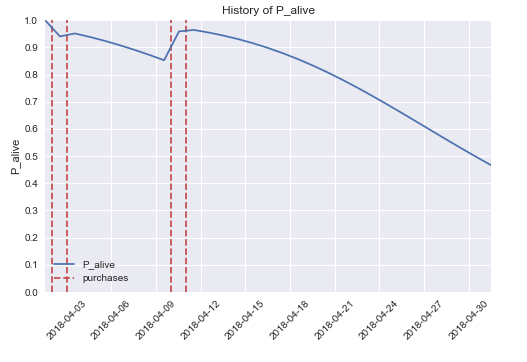
Модель дает прямое руководство к действию для бизнеса: предпринять маркетинговые меры по отношению к пользователю, когда его вероятность активности снижается ниже определенного уровня, чтобы предотвратить его уход.
Эта модель была предложена Fader, Hardie and Lee и называется Beta Geometric / Negative Binomial distribution model (BG/NBD).
BG/NBD модель обладает такими свойствами:
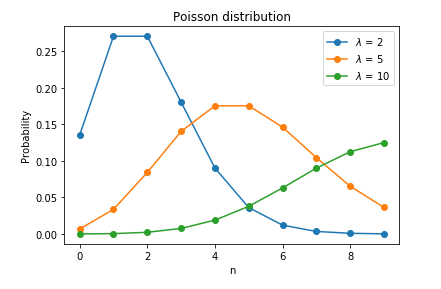
Когда пользователь активен, количество его транзакций за период t описывается распределением Пуассона с параметром транзакций λ.
Распределение Пуассона помогает предсказать происходящие события, используя данные о том, как часто события происходили в прошлом. Например, если пользователь делал в среднем 2 поездки в неделю ( на графике ниже), то вероятность того, что он сделает 3 заказа на следующей неделе равна 0.18.
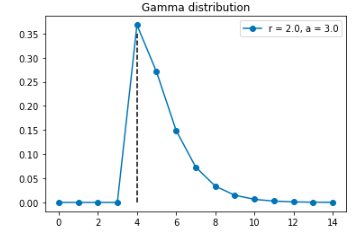
- Гетерогенность параметра транзакций среди пользователей (что означает, как клиенты отличаются друг от друга в покупательском поведении) имеет Гамма распределение с параметрами r (форма) и α (масштаб).
Гамма распределение подходит для процессов со временем ожидания между событиями с распределением Пуассона (в нашем случае для параметра транзакций λ). Например, рассмотрим пользователя, который делает в среднем 2 транзакции в неделю. В таком случае, вероятность того, что время ожидания до того, как пользователь сделает 3 покупки будет больше 4 недель, равна области на графике справа от вертикальной пунктирной линии (под голубой линией распределения) — 0.13.
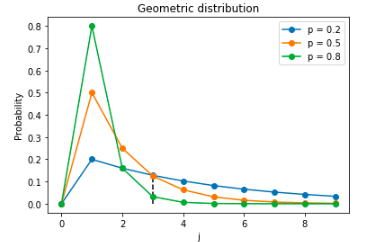
- Пользователи могут стать неактивными после любой транзакции с вероятностью p, и точка их ухода (когда они становятся неактивными) распределена между покупками по Геометрическому закону.
Геометрическое распределение похоже на Бернулли исходы и используется для моделирования количества исходов до (и включая) первый успешный исход. Если для некоторого пользователя , то его вероятность быть неактивным после 3 транзакций равна 0.12 (синяя линия на графике).
- Гетерогенность (вариации между пользователями) в вероятности ухода имеет Бета распределение с параметрами формы α и β.
Бета распределение лучшим образом подходит для представления вероятностных распределений вероятностей — случай, когда мы не знаем вероятность заранее, но у нас есть некоторое обоснованные априорные предпосылки, описываемые α и β (мат. ожидание Бета распределения .
Для предыдущего примера с пользователем, у которого априорная вероятность ухода равна 0.2, оранжевая линия на графике с и
описывает функцию плотности вероятности для вероятности ухода пользователя.

- Параметр транзакций и вероятность ухода независимо распределены между пользователями.
Математическая нотация для признаков пользователя X:
где — число транзакций за некоторый период времени
, и
— время последней покупки.
Основываясь только на этих признаках, модель предсказывает будущие покупательские предпосылки пользователей:
— вероятность
транзакций за период
в будущем,
— ожидаемое число транзакций за период для пользователя с определенным поведением.
Теперь мы можем найти эти два главных показателя. Не вдаваясь в детали, я покажу финальные формулы (больше выкладок в статьях).
Вероятность быть активным:
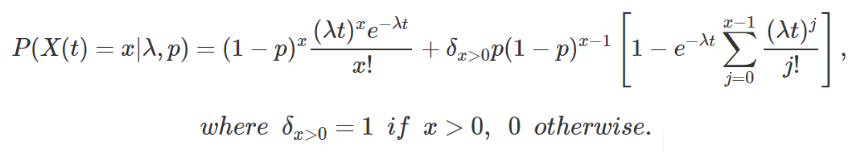
Ожидаемое число транзакций:
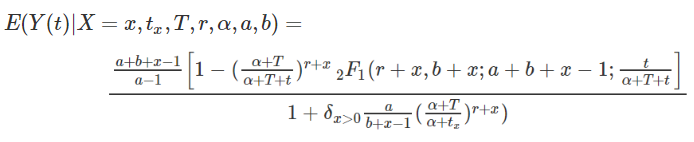
где — гипер-геометрическая функция Гаусса

Гамма-гамма модель для оценки LTV
До этого момента, мы использовали только частоту и недавность покупок клиента. Но в дополнение к этому, мы можем применить денежную составляющую его транзакций. Добавим новые данные в наш пример: пользователь сделал эти 4 поездки по цене 10, 12, 8, 15. Гамма-гамма модель помогает предсказать наиболее вероятную ценность транзакции в будущем.
Суммирую все вместе, теперь у нас есть все элементы, чтобы определить LTV клиента:
LTV = ожидаемое число транзакций цена транзакии
маржа
где первый элемент из BG/NB модели, второй — из Гамма-гамма модели, а маржа устанавливается бизнесом.
Математическая нотация для гамма-гамма модели:
Пользователь совершил транзакций с ценностью
и
— наблюдаемое среднее ценности транзакции.
— скрытое среднее ценности транзакции, и то, что нам интересно —
— ожидаемая денежная ценность пользователя, основанная на его покупательском поведении.
Свойства Гамма-гамма модели:
Денежная ценность транзакций пользователя случайна и находится в пределах их средних транзакционных ценностей.
Средняя ценность транзакции варьируется среди пользователей, но не варьируется для конкретного пользователя во времени.
Средняя ценность транзакции имеет Гамма распределение среди пользователей.
В статьях подробно описывается вывод формулы через еще несколько Гамма распределений. В итоге получается:
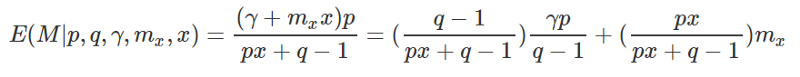
где p параметр формы и v параметр масштаба гамма распределения для транзакций параметр формы и
параметр масштаба для гамма распределения v (допущение модели, что p постоянно — коэффициенты вариации на индивидуальном уровне одни и те же для пользователей). Чтобы найти параметры модели, мы можем использовать метод максимума правдоподобия.
Мы закончили с математикой и теперь мы можем оценить LTV пользователей. Но что насчет точности этой модели?
Оценка точности модели
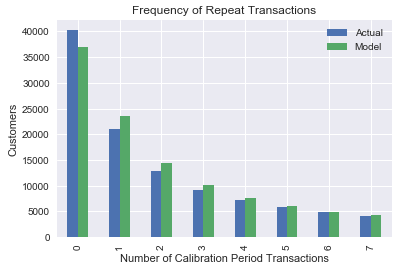
Традиционный подход предлагает разделить данные на две группы — часть для тренировки, часть для теста. В статьях авторы показывают, что их подход работает хорошо. Я тоже попробовала эти модели на реальных данных и тоже получила похожие результаты.
График показывает распределение реальных и предсказанных транзакций для данных из тестовой группы: ошибка здесь составляет 2.8%.
Как применять
Как я говорила в начале, все модели уже имплементированы. Например, библиотека Python “lifetimes” содержит все функции и метрики, необходимые, чтобы определить LTV. Детально написанная документация содержит много примеров и объяснений. Там также есть примеры sql запросов, чтобы получать данные в необходимом формате. Так что приступить к работе можно всего за несколько минут.
Заключение
В этом посте, я показала в деталях, как LTV пользователей может быть оценено, используя только несколько признаков.
Я хочу заметить, что иногда можно отойти от часто используемых gradient boosted trees и попробовать другие подходы, которые имеют сравнимый уровень точности. Статистическое обучение все еще может быть использовано на практике и может помочь бизнесу лучше понимать клиентов.
References
Fader, Peter & G. S. Hardie, Bruce & Lok Lee, Ka. (2005). “Counting Your Customers” the Easy Way: An Alternative to the Pareto/NBD Model. Marketing Science.
Fader, Peter & G. S. Hardie, Bruce (2013). The Gamma-Gamma Model of Monetary Value.
Fader, Peter S., Bruce G. S. Hardie, and Ka Lok Lee (2005), “RFM and CLV: Using Iso-value Curves for Customer Base Analysis,” Journal of Marketing Research.