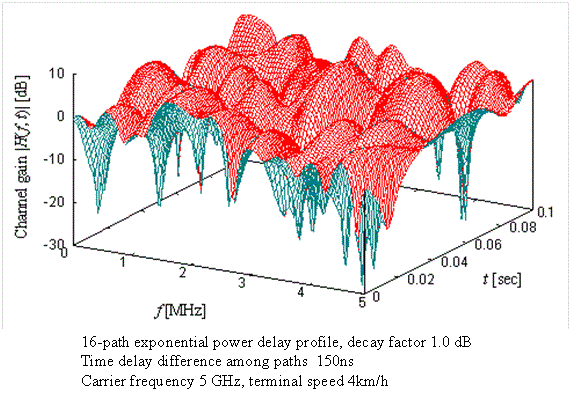
Всем доброго времени суток!
Рассматривая тему пространственного разнесения, вскользь мы уже коснулись и вопросов замираний в каналах связи, и того, почему такие замирания возникают. Сегодня предлагаю поговорить об этой теме чуть более подробно.
Более того, в сегодняшней статье мы слегка коснемся вопросов пространственной корреляции MIMO каналов, которые традиционно разбираются в рамках курса профессора Хаардта "Mobile communications" (CSP), и поэтому, я думаю, такая публикация тем более не будет лишней. И, отмечу сразу, круг вопросов не ограничивается применением только в мобильной связи.
В общем, всех интересующихся тематикой беспроводной связи приглашаю к прочтению, и поехали!

Colin Slater "Fading memories". Да, сводить всё к одной теме — это, наверное, перебор, однако какой-то такой метафорой, я думаю, можно представить, что именно получает приемник после всевозможных воздействий на изначальный, информационный сигнал...
О чем вообще идет речь?
Начнем с того, что в природе существуют, так называемые, мультипликативные помехи, влияющие на принимаемую мощность сигнала — замирания (fading).
В англоязычной литературе термин fading предполагает некое влияние, которое, как бы, заставляет наш сигнал затухать, "увядать".
В нашей литературе обычно применяется именно термин замирания, а связано это в первую очередь с эффектом многолучевого распространения: если электромагнитная волна встретится со своей копией, порожденной отражениями и дифракцией, и они будут при этом в противофазе, то волны друг друга погасят — то есть канал, как бы, замрет.
Замирания бывают быстрыми и медленными (fast and slow fading).
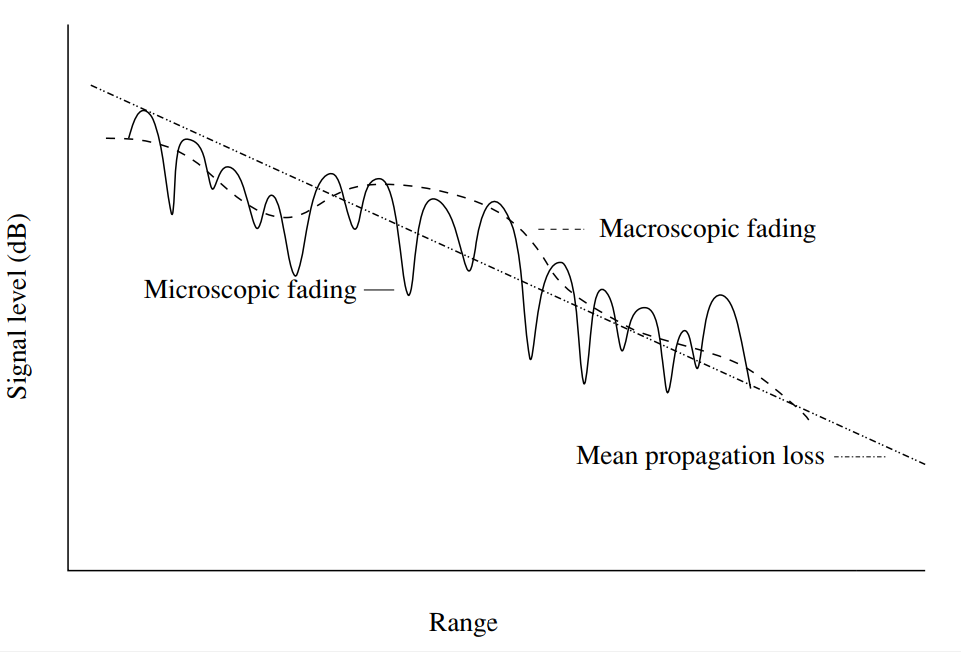
Рис. 1. Колебания мощности сигнала в беспроводных каналах в зависимости от расстояния. Средний уровень потерь распространения монотонно увеличивается с увеличением дальности. Локальные отклонения могут возникать из-за макроскопических (медленных) и микроскопических (быстрых) замираний [1, с.14 ].
Сознаюсь сразу, сегодня с медленными замираниями мы работать не будем, а вот про быстрые поговорим достаточно подробно.
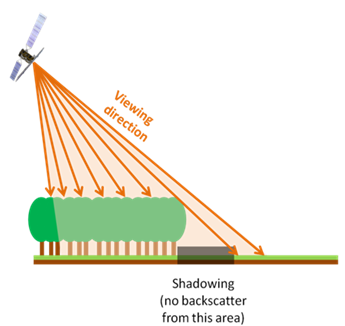
Рис. 2. Иллюстрация эффекта затенения: как правило, медленные замирания возникают из-за затенений (shadowing). Для моделирования обыкновенно выбирают логнормальное распределение.
Желающих почитать немного про медленные замирания, в частности, и про то, как можно моделировать спутниковые каналы, в целом, приглашаю сюда!
Быстрые замирания
Быстрые замирания возникают, как правило, по двум основным причинам:
- из-за уже упомянутого нами многолучевого распространения (multipath propagation) и/или
- из-за Допплеровских сдвигов частоты.
Последние очень заметны для спутниковых систем, однако не всегда учитываются для случаев наземной связи из-за того, что базовые станции в данном случае, как правило, неподвижны.

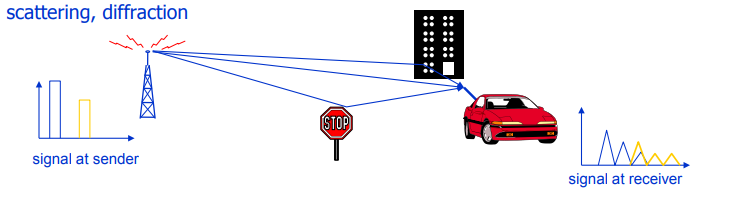
Рис. 3. Иллюстрация причин возникновения замираний. Отдельное внимание уделено рассеиванию (scattering) и дифракции: именно в силу данных явлений и формируется, так называемое, многолучевое распространение, приводящее к межсимвольным помехам (ISI).
Но и это ещё далеко не всё.
Selective fading vs. Flat fading
Выше мы разделили наши помехи по характеру возникновения. Однако, помехи можно разделить ещё и по характеру воздействия на передаваемый сигнал. И здесь нам понадобится понятие избирательности канала.
Приведем небольшую классификацию по [1, c. 14-18]. Итак, быстрые замирания могут быть:
- Избирательными (selective)
а. Частотно избирательными (frequency selective)
б. Избирательными во временной области (time selective)
в. Пространственно избирательными (это относится к вопросу об углах прихода и отправки ЭМ волн — сегодня мы этот вопрос разбирать не будем) - Плоскими (flat) — тяготеющими больше к характеру медленных замираний (да, вот такой вот парадокс)
Что подразумевает последний термин, объясним от обратного.
Во-первых, если ширина спектра передаваемого нами сигнала превышает когерентную полосу пропускания канала, то говорят, что мы имеем дело с частотно-селективными помехами.
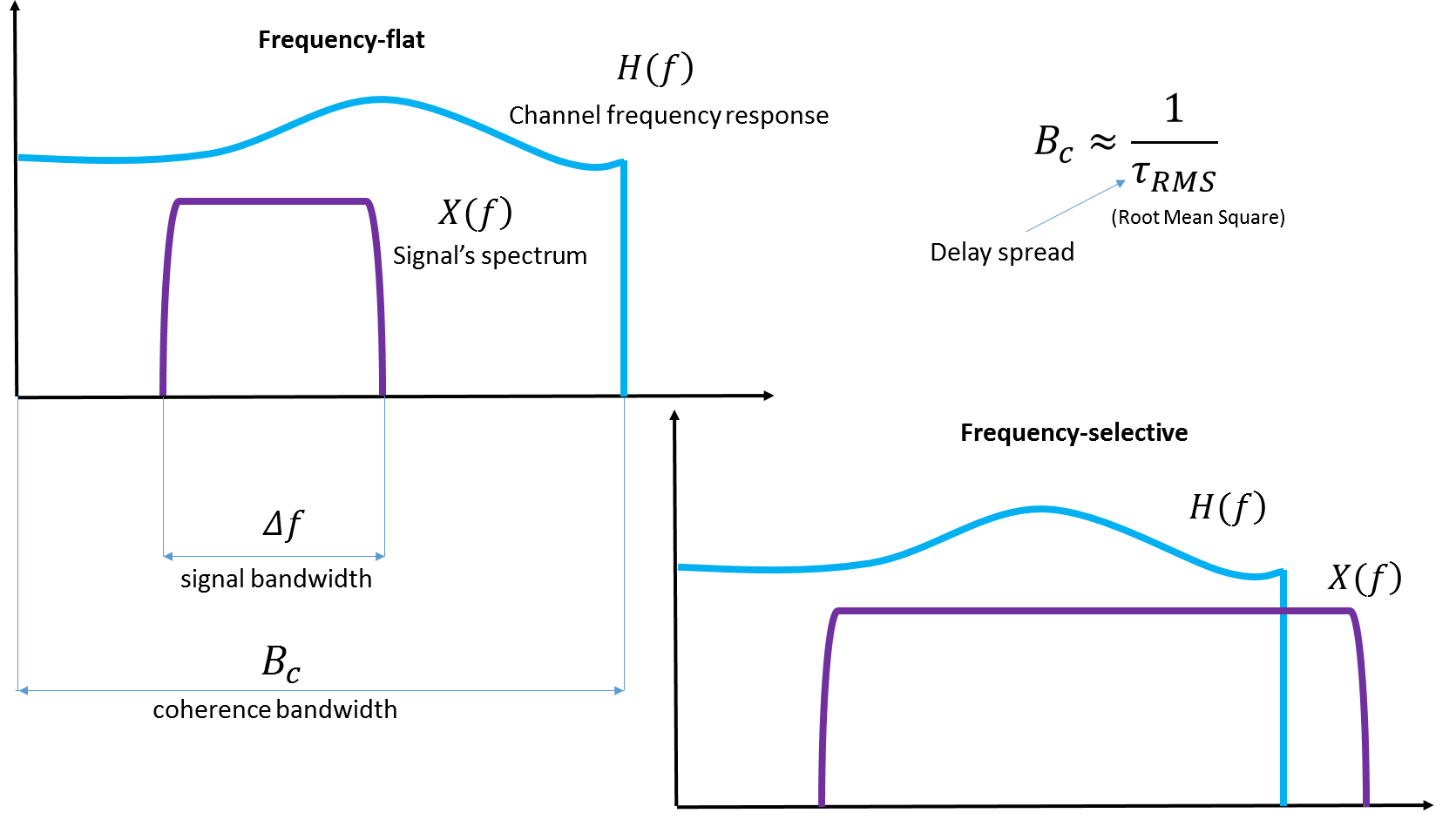
Рис. 4. Иллюстрация когерентной полосы пропускания. Думаю, не будет моветоном прикрепить иллюстраций из Вики, если сам их туда и добавил.
Обратите внимание на переменную Delay spread — разброс задержек. Именно этот разброс в задержках между приходом разных копий одного сигнала и измеряют, когда определяют характеристики того или иного реального канала.
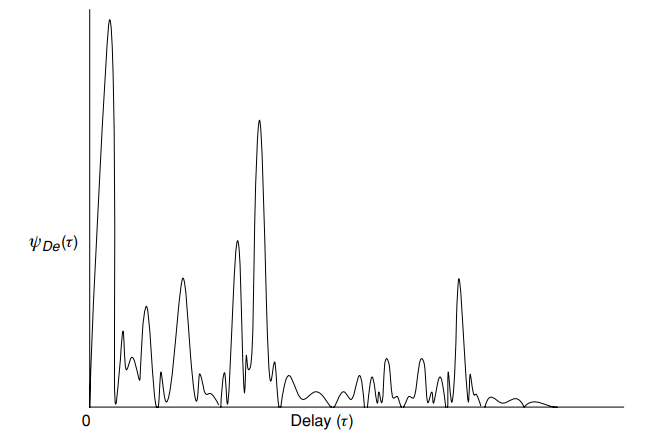
Рис. 5. Типичный профиль задержки (мощности) — средняя мощность как функция задержки
.[1, c. 16]

Рис. 6. Частотно-селективный, но не избирательно по времени канал.
Например, для S-диапазона (интересовался, когда искал информацию по спутниковым системам) Bc = 0.5 – 2 МГц (Kanatas A. G., Panagopoulos A. D. (ed.). Radio Wave Propagation and Channel Modeling for Earth–Space Systems. – CRC Press, 2016. — с. 107).
Это очень хорошо ложится на бодовую скорость, например, такого спутникового приёмопередатчика. И здесь нет ничего удивительного: символьная скорость линейных типов цифровой модуляции (PSK, QAM, OFDM) совпадает с полосой, занимаемой сигналом (см. Goldsmith A. Wireless communications. – Stanford University, 2004. — c. 140, 326), а значит хорошо бы попробовать втиснуть сигнал в когерентную полосу по максимуму. Частоты — это всё-таки ценный ресурс.
Во-вторых, если длина нашего сигнала во временной области превышает время когерентности канала, то говорят, что мы имеем дело с каналом, изменяющимся во времени.
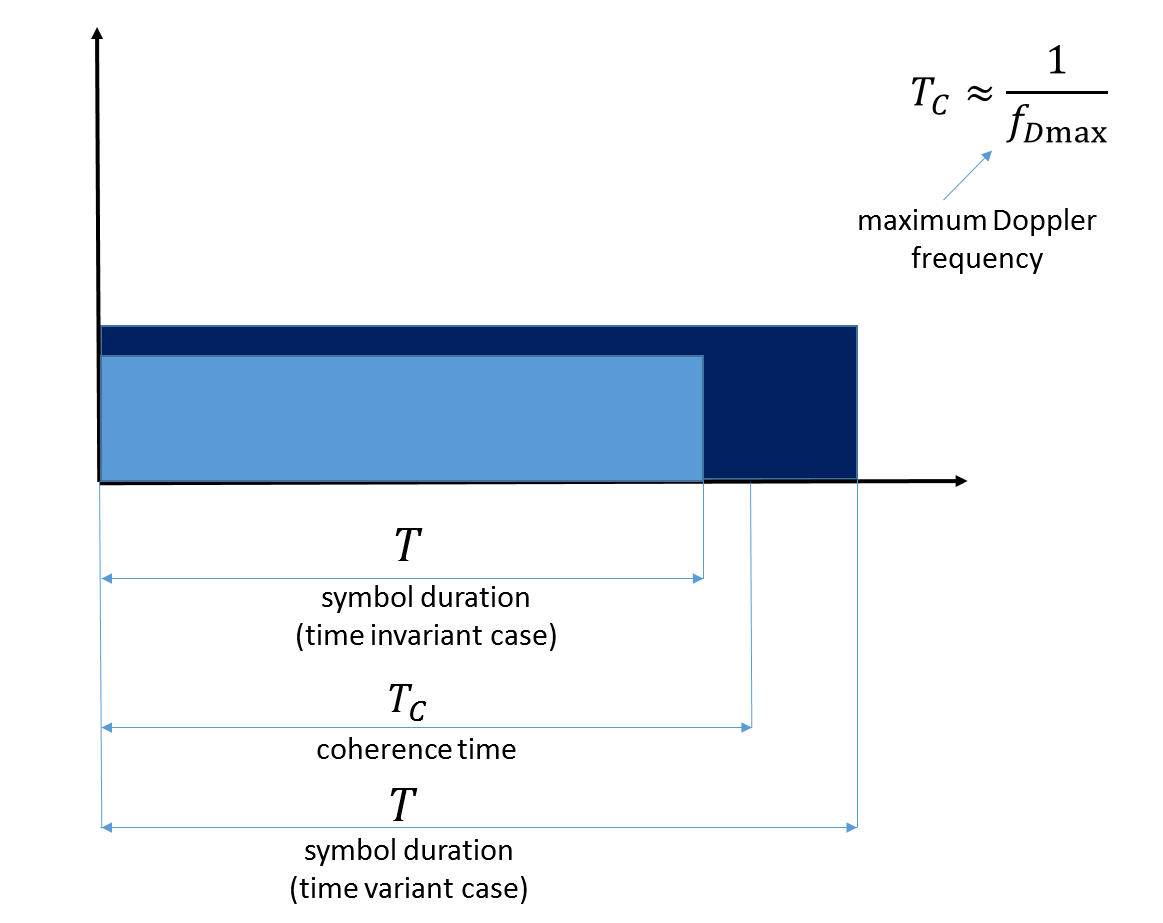
Рис. 7. Иллюстрация времени когерентности. Обратите внимание, здесь максимальная допплеровская частота отражает движение самого мобильного терминала.

Рис. 8. Почти неизбирательный по частоте, но избирательный по времени: быстро затухающий канал.
Ну, и соответственно, если нам удастся каким-то чудом избежать вышеперечисленного, то мы придем к самомому простому и удобному случаю — к плоским замираниям [1, c. 14-18][2, c. 88-92].
Самый простой канал с замираниями
Возможно, вы где-то уже встречали подобный способ моделирования плоского канала с замираниями:
h = (1/sqrt(2))*(randn(size(msg)) + 1j*randn(size(msg))) % MatLab / Octave
Что подразумевается:
- отсутствие прямой видимости (вполне оправданный для наземной связи случай)
- узкополосный канал (narrowband channel) — вписались в когерентную полосу
- кстати, пример широкополосного канала мы рассматривали в данной статье (рис. 4).
- частотной селективности тоже нет — вписались в когерентное время
- отсутствие затенений и Допплеровских сдвигов частоты
То есть вот он собственной персоной: плоский канал с замираниями. Для случая без прямой видимости канал ещё называют к тому же рэлеевским.

Лорд Рэлей
Из чего проистекает такая модель?
Во-первых, говоря о современных системах связи, мы скорее всего подразумеваем работу с цифровыми сигналами. Более того, работаем мы к тому же скорее всего c квадратурными типами модуляции (I/Q), то есть с сигналами комплексными.
Рис. 9. Сигнальное созвездие QPSK. Полярные координаты, единичная окружность. Например, символу 11 будет соответствовать координата равная примерно 0,7+0,7i.
Логично предположить воздействие помех как на реальную, так и на мнимую составляющую. Более того, стоит вслед за Центральной предельной теоремой предположить также гауссовский характер таких воздействий. Запишем формулой [1, с. 39]:
где и
— это нормально распределенные случайные величины.
Чаще всего используется модель с нормированной средней мощностью:
А значит .
Если мы предполагаем независимые искажения составляющих огибающей сигнала: как синфазной (I — In-phase), так и квадратурной (Q — Quadrature), — то положение числа, на которое будет перемножен изначальный символ (отсюда мультипликативность помехи), в полярных координатах может быть вычислено буквально по теореме Пифагора:
где и
— это тоже нормально распределенные случайные величины. Для нормированной мощности
,
.
И вот перед нами формула рэлеевского процесса! [2, с.78 ]
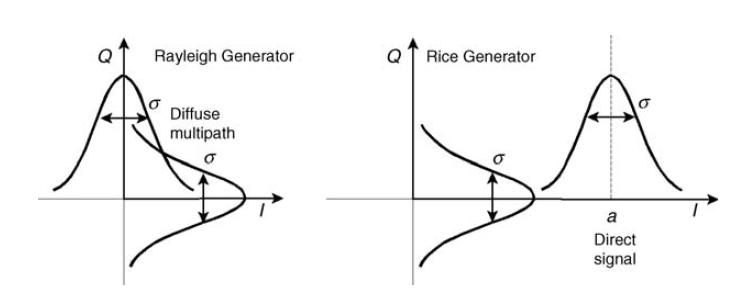
Рис. 10. Гауссовские генераторы в квадратуре для моделирования замираний Рэлея и Райса [3, p.125]. О райсовском канале мы поговорим чуть позже.
Лично мне очень нравится пример с пристрелкой пушек: если две пушки будут стрелять перпендикулярно друг другу достаточное количество раз, то для каждой по отдельности распределение попаданий будет нормальным, а общее распределение попаданий рэлеевским. Вот что-то подобное происходит и с нашими помехами.
Если мы рассматриваем самый простой случай без какой-либо пространственной корреляции между каналами (допустим, что у нас есть несколько пространственных каналов — MIMO), то говорят, что канал пространственно белый — spatially white. А так как все каналы независимы, то, следовательно, и "генерить" можно не только случайные величины, распределенные по Рэлею, но и вектора, и матрицы, и тензоры [3, c.125 ]:
где и
— это матрицы, состоящие из нормально распределенных значений.
Тут всё довольно просто: как мы уже сказали выше, мощность отклика канала должна быть равна единице, т.е.:
Именно за этим и вводят масштабирующий фактор .
Продемонстрируем (возьмем python для разнообразия):
import numpy as np
N = int(1e6)
h = 1/np.sqrt(2)*(np.random.randn(N) + 1j*np.random.randn(N))
P = np.mean(h*np.conj(h))
print(np.round(P))
>>> (1+0j)Подытожим:
Помеховая компонента при отсутствии прямой видимости может быть описана как n-мерный вектор (в зависимости от размерности канала) независимых идентично распределенных (IID — independent identically distributed) по комплексному гауссовскому закону с круговой симметрией и нулевым мат. ожиданием (ZMCSCG — zero-mean circularly symmetric complex Gaussian) чисел.
Целая скороговорка!
Почти самый простой канал с замираниями
Хорошо, а если прямая видимость всё-таки есть? Может быть, есть на этот счет уже готовые математические модели?
Конечно, есть! Например такая [4], обобщенная для случая с несколькими приёмными и передающими антеннами (MIMO):
где — это собственно и есть комплексная огибающая импульсной характеристики канала (или канальная матрица, если речь идет о MIMO),
— это компонента прямой видимости (Line-of-Sight), а
— это компонента отсутствия прямой видимости (Non-Line-of-Sight), её мы уже рассмотрели.
Обратите внимание на переменную K — это так называемый райсовский фактор (Rician/Ricean factor) — отношение мощности прямого пути распространения к мощности всех остальных путей. Именно он определяет, насколько сильно будет подвержен наш канал помехам.
Слагаемое представляет из себя математическое ожидание канальной матрицы и моделироваться может исходя из геометрии приемных и передающих массивов антенн:
где и
— это отклики приемного и передающего массивов антенн сответственно, а
и
— это углы прихода (angle of arrival) и отправки (angle of departure).
Множители, в общем-то, симметричные и могут быть описаны общей формулой:
где — это расстояние между антеннами (antenna spacing) в длинах волн, а
— это количество элементов в массиве антенн (рис. 11).
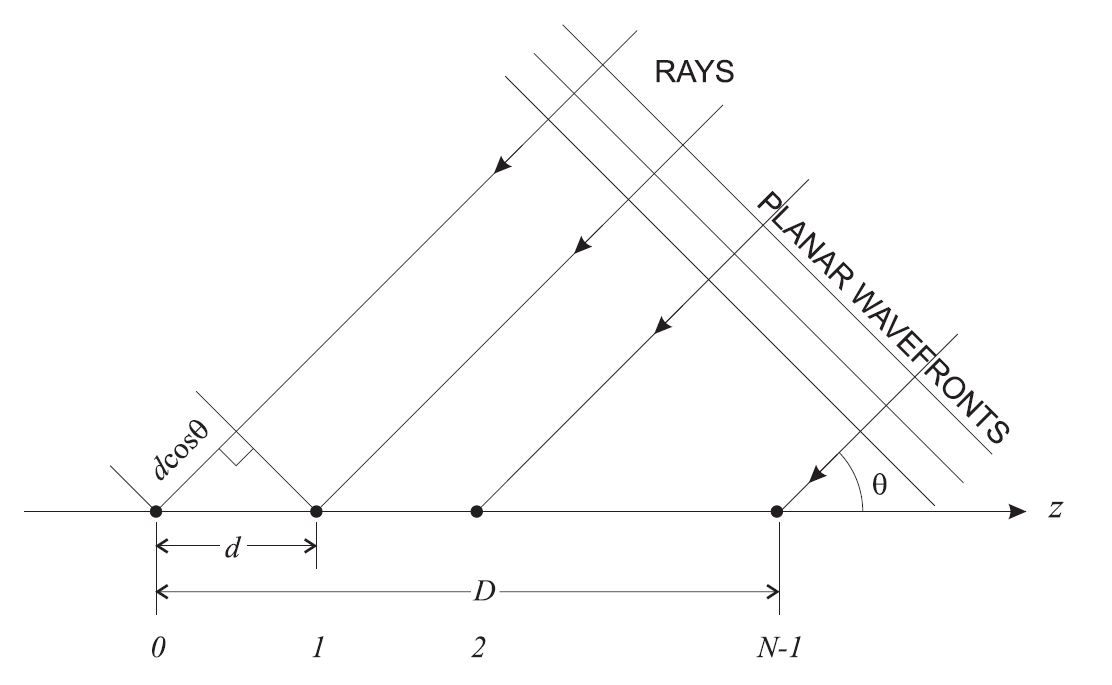
Рис. 11. Геометрия линейного массива. Для случая Massive MIMO геометрия, конечно, будет уже другой. Подробнее об этом прочитать можно, например, здесь.
Ну, а теперь, когда модель хоть сколько-то разобрана, можно её и упростить.
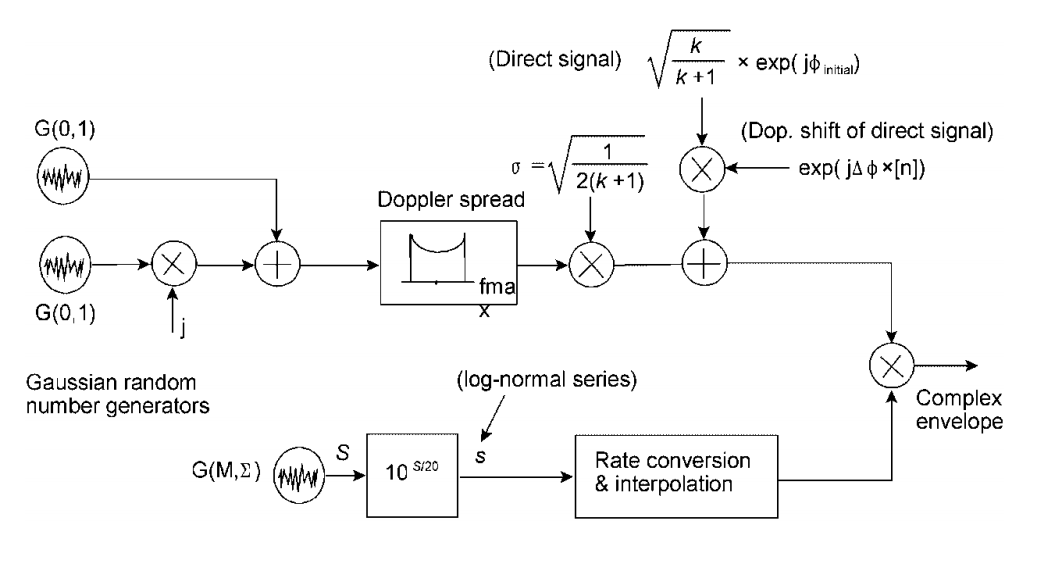
Для случая SISO (самого простого и базового) формула (5) примет вид:
ибо для 1 передающей и 1 приемной антенны .
И это, как нельзя кстати, подходит под модель на рисунке 12.
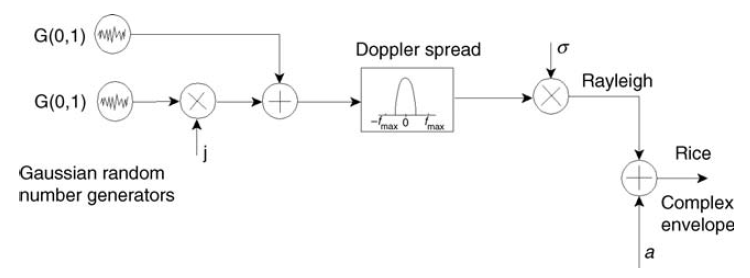
Рис. 12. Схема формирования канала Райса (узкополосный сигнал) [3, p.127]. При канал будет всё больше вырождаться в Рэлеевский. Поэтому я и употребил слово почти в подзаголовке: канал Рэлея — это частный случай канала Райса. Это также видно из формулы (5).
Поясним: — это райсовский масштабирующий параметр (Rician scale parameter), а
— это параметр не-центральности (Rician noncentrality parameter).
Вообще, для целей моделирования Doppler Spread чаще всего вам скорее всего будет попадаться модель Джейкса (Jakes model, U-shape), основанная на технике суммирования синусоид (Sum-of-sinusoids Technique). Теоретически спектр такой модели выглядит так:

Спектральная плотность мощности рэлеевского затухания с максимальным доплеровским сдвигом 10 Гц. Источник.
Однако, в жизни, судя по [1, c. 15] такой спектр выглядит всё-таки менее ровно:

Типичный доплеровский (энергетический) спектр — средняя мощность как функция доплеровской частоты
[1, c. 15].
Ожидания… Реальность.
Например такая для модели Corazza-Vatalaro (С&V):
см. Fontan, F. P., Mayo, A., Marote, D., Prieto‐Cerdeira, R., Mariño, P., Machado, F., & Riera, N. (2008). Review of generative models for the narrowband land mobile satellite propagation channel. International Journal of Satellite Communications and Networking, 26(4), 291-316.
Но это уже совсем другая история...
Моделирование почти самого простого канала с замираниями в MatLab
Сверим полученные выкладки с чем-нибудь уже проверенным. Например, со специальными функциями MatLab.
Для проверки модели со своей стороны сгенерируем случайное двоичное сообщение (длина сообщения равна 100000 бит ), промодулируем его с помощью M-PSK или M-QAM, поэлементно умножим с процессом замираний, добавим белый гауссовский шум, выровняем эквалайзером Zero-Forcing, демодулируем и рассчитаем битовую ошибку (BER — bit error ratio) (рис. 13). Количество испытаний будет равным ста.
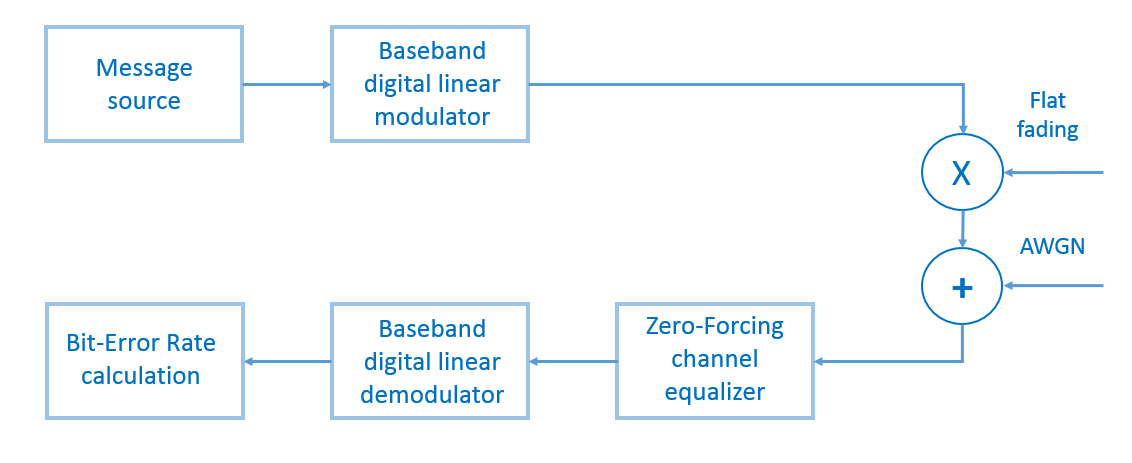
Рис.13. Блок-схема модели системы передачи, которую опишет наш скрипт.
И скачать здесь.
clear all; close all; clc
EbNo = 0:40;
K = [4.0; 0.6];
M = [4; 8; 16; 64; 256]; %Positions of modulation (M-PSK or M-QAM)
for k = 1:length(K)
for m = 1:length(M)
message = randi([0, M(m)-1], 100000, 1);
if M(m) >= 16
mod_msg = qammod(message, M(m), pi/4, 'gray');
ric_ber(:, m, k) = berfading(EbNo,'qam',M(m),1,K(k));
else
mod_msg = pskmod(message, M(m), pi/4, 'gray');
ric_ber(:, m, k) = berfading(EbNo, 'psk', M(m), 1, K(k));
end
Es = mean(abs(mod_msg).^2);
No = Es./((10.^(EbNo./10))*log2(M(m)));
h = sqrt( K(k)/(K(k)+1)) +...
sqrt( 1/(K(k)+1))*(1/sqrt(2))*(randn(size(mod_msg))...
+ 1j*randn(size(mod_msg)));
ric_msg = mod_msg.*h; % Rician flat fading
for c = 1:100
for jj = 1:length(EbNo)
noisy_mod = ric_msg +...
sqrt(No(jj)/2)*(randn(size(mod_msg))+...
1j*randn(size(mod_msg))); %AWGN
noisy_mod = noisy_mod ./ h; % zero-forcing equalization
if M(m) >= 16
demod_msg = qamdemod(noisy_mod, M(m), pi/4, 'gray');
else
demod_msg = pskdemod(noisy_mod, M(m), pi/4, 'gray');
end
[number,BER(c,jj)] = biterr(message,demod_msg);
end
end
sum_BER(:,m, k) = sum(BER)./c;
end
end
figure(1)
semilogy(EbNo, sum_BER(:,1,1), 'b-o', EbNo, sum_BER(:,2,1), 'r-o',...
EbNo, sum_BER(:,3,1), 'g-o', EbNo, sum_BER(:,4,1), 'c-o',...
EbNo, sum_BER(:,5,1), 'k-o',...
EbNo, ric_ber(:,1,1), 'b-', EbNo, ric_ber(:,2,1), 'r-',...
EbNo, ric_ber(:,3,1), 'g-', EbNo, ric_ber(:,4,1), 'c-',...
EbNo, ric_ber(:,5,1), 'k-', 'LineWidth', 1.5)
title('Rician model (K = 4.0)')
legend('QPSK(simulated)', '8-PSK(simulated)',...
'16-QAM(simulated)', '64-QAM(simulated)' ,'256-QAM(simulated)',...
'QPSK(theory)','8-PSK(theory)', '16-QAM(theory)',...
'64-QAM(theory)' ,'256-QAM(theory)','location','best')
xlabel('EbNo (dB)')
ylabel('BER')
grid on
figure(2)
semilogy(EbNo, sum_BER(:,1,2), 'b-o', EbNo, sum_BER(:,2,2), 'r-o',...
EbNo, sum_BER(:,3,2), 'g-o', EbNo, sum_BER(:,4,2), 'c-o',...
EbNo, sum_BER(:,5,2), 'k-o',...
EbNo, ric_ber(:,1,2), 'b-', EbNo, ric_ber(:,2,2), 'r-',...
EbNo, ric_ber(:,3,2), 'g-', EbNo,ric_ber(:,4,2), 'c-',...
EbNo, ric_ber(:,5,2), 'k-','LineWidth', 1.5)
title('Rician model (K = 0.6)')
legend('QPSK(simulated)', '8-PSK(simulated)',...
'16-QAM(simulated)', '64-QAM(simulated)' ,'256-QAM(simulated)',...
'QPSK(theory)','8-PSK(theory)',...
'16-QAM(theory)', '64-QAM(theory)' ,'256-QAM(theory)','location','best')
xlabel('EbNo (dB)')
ylabel('BER')
grid onДолжно получится что-то такое:
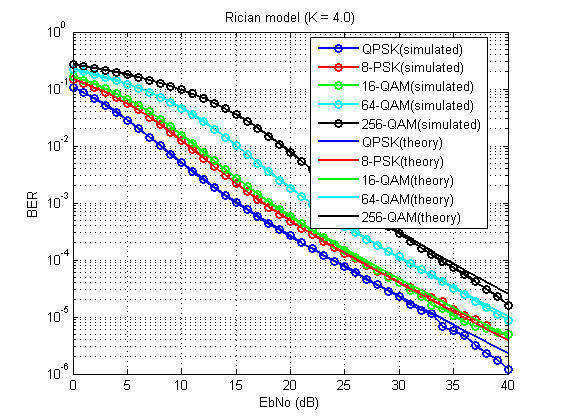
Рис. 14. Коэффициент битовых ошибок для рассмотренной модели (К = 4.0).
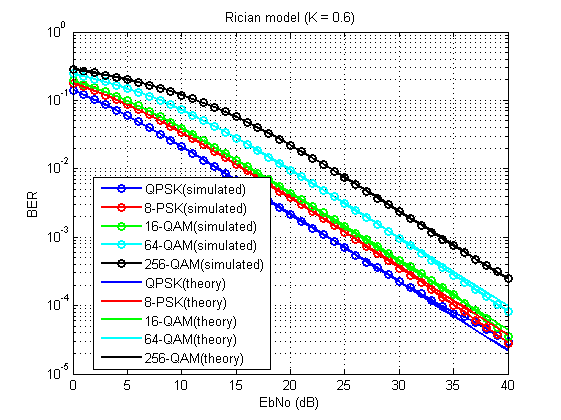
Fig. 15. Коэффициент битовых ошибок для рассмотренной модели (K = 0.6).
Не без огрехов, конечно (из-за ограниченности по количеству усреднений), но в целом, видно, что работает!
Для этого примем одно допущение: канальная матрица будет состоять из независимых путей распространения, каждый из которых будет распределен по Райсу.
При каких условиях это возможно?
Как мы уже отметили выше, IID компонента может быть сгенерирована в любой размерности. Значит любой пространственно белый канал MIMO без прямой видимости может быть смоделирован как сэт скольки-то (зависит от размерности канала) SISO каналов.
С компонентой прямой видимости немного сложнее — нужно ведь учитывать положение решеток.
Рассмотрим формулу (5): если наша матрица компонента прямой видимости будет состоять только из единиц , то кажется, что райсовская составляющая тоже становится пространственно белой.
Чтобы к этому подойти, запишем компоненту прямой видимости более подробно, чем в формуле (6):
Бросается в глаза, что если , то матрица и будет состоять из одних единиц. Геометрически это ситуация, когда два массива элементов ориентированы строго друг на друга:
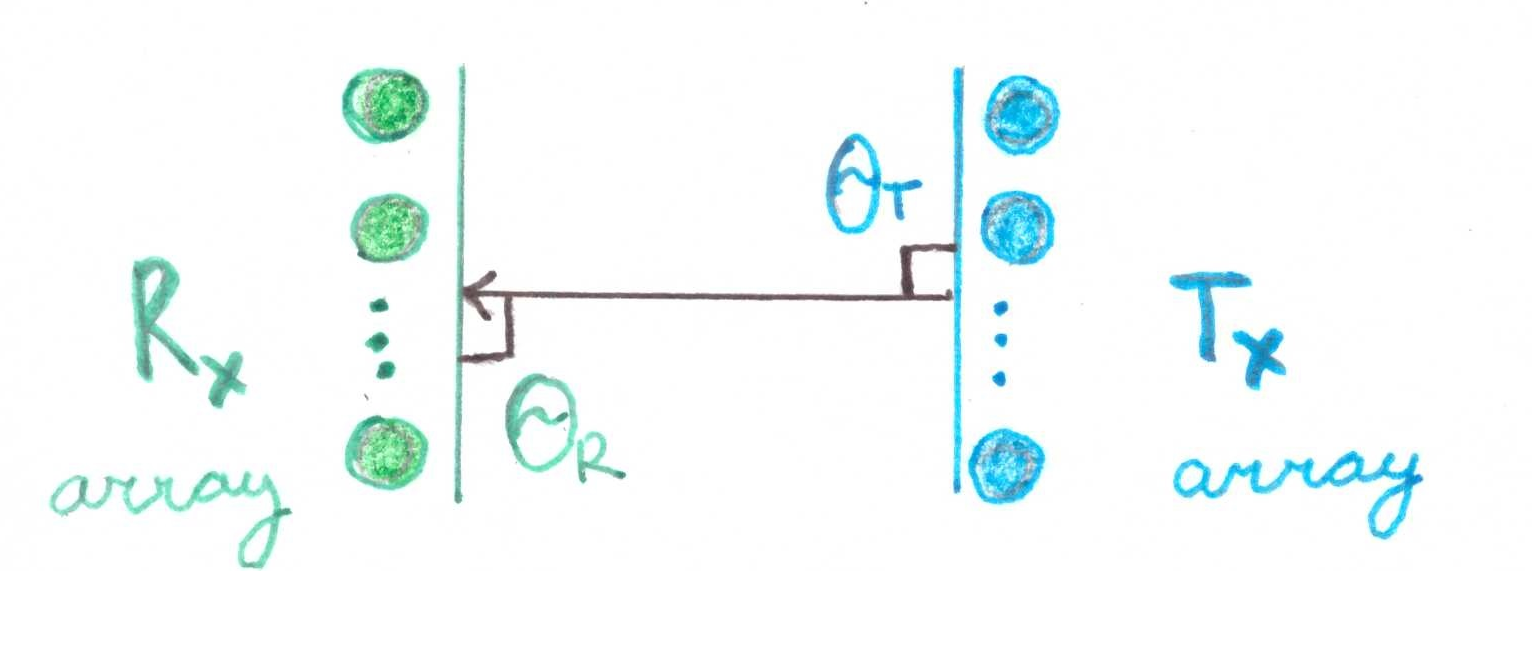
Проведем небольшую математическую демонстрацию:

Для моделирования возьмем за основу схему Аламоути. Получится должно что-то такое:
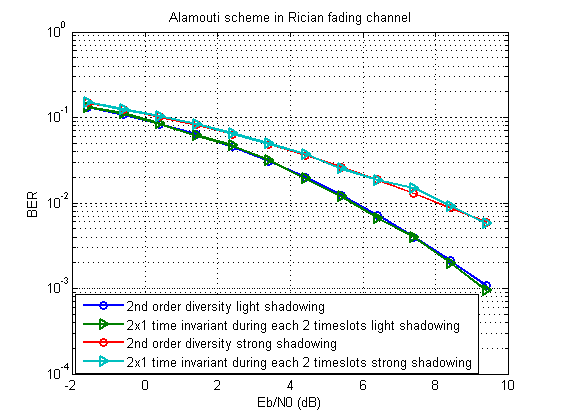
Дополненный скрипт можно скачать здесь.
Well done.
Почти самый простой канал с замираниями и пространственная корреляция
А теперь, завершая наше путешествие в мир статистических выкладок, давайте немного приблизимся к реальности.
Выше мы рассматривали случай, когда компонента отсутствия прямой видимости была пространственно белой. Однако, от реальных систем стоит всё-таки ждать некоторой корреляции между антеннами, а значит и между путями распространения ЭМ волны.
Введем новую переменную — матрицу пространственной корреляции:
где vec обозначает операцию векторизации. Влиять эта матрица будет, кстати, только на компоненту отсутствия прямой видимости, и значит в данном случае .

Резонно предположить, что в реальной жизни сначала через замеры определяют данную матрицу, а уже потом используют её для моделирования:
где — это IID матрица (w означает spatially white).
Обратите внимание, возведение матрицы в степень — это не возведение в степень каждого её элемента. Следовательно в нашем случае в MatLab нельзя использовать функцию sqrt(). Использовать нужно оператор ^.
В случае Python нельзя использовать оператор возведения в степень ** и метод sqrt популярного модуля numpy. Использовать нужно метод fractional_matrix_power модуля scipy.
Если приёмник и передатчик достаточно независимы друг от друга, как на рисунке 16, то можно применить модель Кронекера [1, c. 40], чтобы уменьшить количество коэффициентов для расчета:
где обозначает произведение Кронекера.

Леопольд Кронекер
Отдельно рассмотрим составляющие выражение матрицы:
— это матрица корреляции приемных антенн,
— это матрица корреляции передающих антенн
и
— это количество приемных и передающих антенн соответственно. Обе матрицы являются положительными полуопределенными (positive semi-definite) Эрмитовыми (Hermitian) матрицами. Более того, ранг матрицы
ограничен значением
.

Рис. 16.
Модель рассеивателей в случае некоррелирующих приёмника и передатчика. Зеленые точки означают рассеиватели, синие и красные — приемник и передатчик. Прошу простить за качество, это скриншот по одной из домашек ТУ Ильменау.
Канальную матрицу в данном случае можно записать как:
Однако, для ситуаций, как, например, на рисунке 17, использовать придется всё же полную корреляционную матрицу (см. формулу (9)).
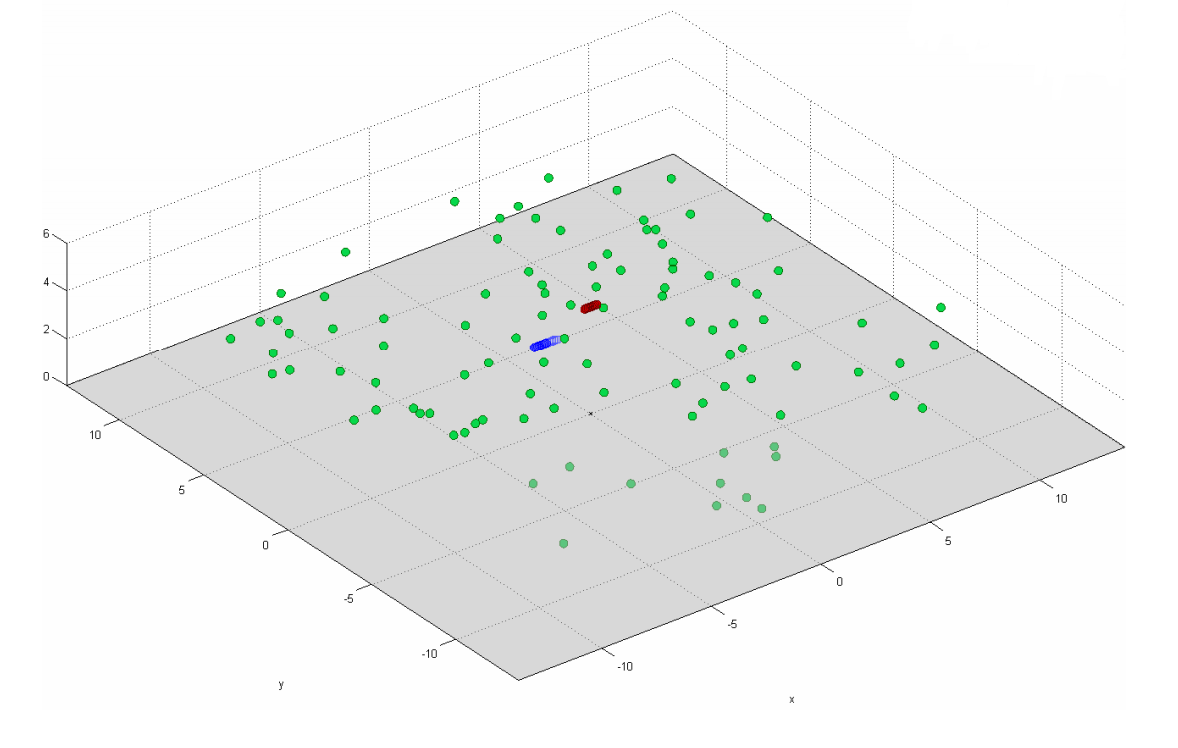
Рис. 17. Модель рассеивателей в случае коррелирующих приёмника и передатчика. Зеленые точки означают рассеиватели, синие и красные — приемник и передатчик.
Дабы закрепить узнанное и посмотреть, насколько осложнит жизнь пространственная корреляция, давайте попробуем посчитать пропускную способность каналов. Например, для MIMO 2x2.
Для этого возьмем следующие случаи (имеем в виду всё те же плоские замирания, для простоты также рассмотрим только рэлеевский канал):
1) Пространственно белый канал;
2) Модель Кронекера с относительно слабой корреляцией:
3) Модель Кронекера с относительно сильной корреляцией:
Использовать в данной части будем Python 3.4. Функцию для расчета пропускной способности возьмем из одной из моих прошлых публикаций.
import numpy as np
from numpy import linalg as LA
import matplotlib.pyplot as plt
from scipy.linalg import fractional_matrix_power
def openloop_capacity(H_chan, SNR_dB):
SNR = 10**(SNR_dB/10)
Mt = np.shape(H_chan)[1]
H_sq = np.dot(H_chan,np.matrix(H_chan, dtype=complex).H)
lambdas = LA.eigvals(H_sq)
lambdas = np.sort(lambdas)[::-1]
c = 0
for eig in lambdas:
c = c + np.log2(1 + SNR*eig/Mt)
return np.real(c)Определим основные параметры системы:
Mr = 2 # number of receive antennas
Mt = 2 # number of transmit antennas
Rr1 = np.array([[1., .4], [.4, 1.]]) # case 1
Rr2 = np.array([[1., .6], [.6, 1.]]) # case 2
Rt1 = np.array([[1., .4], [.4, 1.]]) # case 1
Rt2 = np.array([[1., .6], [.6, 1.]]) # case 2
Rr1_half = fractional_matrix_power(Rr1, 0.5)
Rr2_half = fractional_matrix_power(Rr2, 0.5)
Rt1_half = fractional_matrix_power(Rt1, 0.5)
Rt1_half_H = np.conj(Rt1_half).T
Rt2_half = fractional_matrix_power(Rt2, 0.5)
Rt2_half_H = np.conj(Rt2_half).T
Запускаем моделирование:
counter = 1000
SNR_dBs = [i for i in range(1, 21)]
C_MIMO_uncorr = np.empty((len(SNR_dBs), counter))
C_MIMO_kron1 = np.empty((len(SNR_dBs), counter))
C_MIMO_kron2 = np.empty((len(SNR_dBs), counter))
C_MIMO_kron3 = np.empty((len(SNR_dBs), counter))
C_MIMO_kron4 = np.empty((len(SNR_dBs), counter))
for c in range(counter):
H_uncorr = (np.random.randn(Mr,Mt) + 1j*np.random.randn(Mr, Mt))/np.sqrt(2)
H_kron1 = np.dot(Rr1_half, np.dot(H_uncorr, Rt1_half_H))
H_kron2 = np.dot(Rr2_half, np.dot(H_uncorr, Rt2_half_H))
for idx, SNR_dB in enumerate(SNR_dBs):
C_MIMO_uncorr[idx, c] = openloop_capacity(H_uncorr, SNR_dB)
C_MIMO_kron1[idx, c] = openloop_capacity(H_kron1, SNR_dB)
C_MIMO_kron2[idx, c] = openloop_capacity(H_kron2, SNR_dB)
C_MIMO_uncorr_erg = np.mean(C_MIMO_uncorr, axis=1)
C_MIMO_kron1_erg = np.mean(C_MIMO_kron1, axis=1)
C_MIMO_kron2_erg = np.mean(C_MIMO_kron2, axis=1)
plt.figure(figsize=(7, 5), dpi=100)
plt.plot(SNR_dBs, C_MIMO_uncorr_erg,'g-o', label='Uncorrelated')
plt.plot(SNR_dBs, C_MIMO_kron1_erg, 'm-o', label='Kronecker model, case 1')
plt.plot(SNR_dBs, C_MIMO_kron2_erg, 'r-o', label='Kronecker model, case 2')
plt.title("Rayleigh flat fading (MIMO 2x2)")
plt.xlabel('SNR (dB)')
plt.ylabel('Ergodic capacity (bps/Hz)')
plt.legend()
plt.minorticks_on()
plt.grid(which='major')
plt.grid(which='minor', linestyle=':')
plt.show()
Получаем:
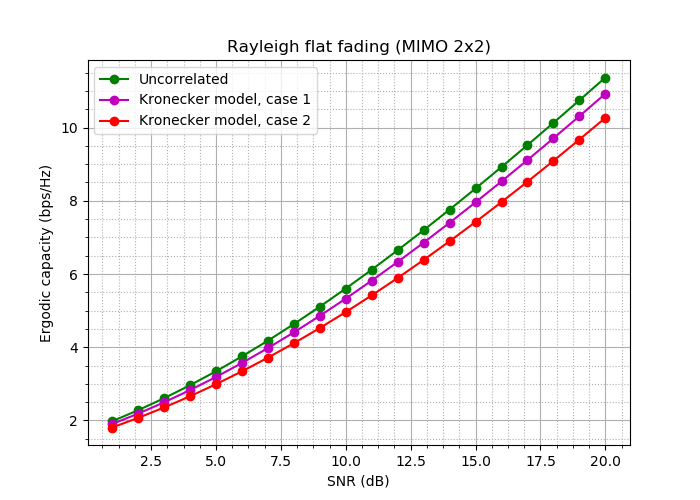
Рис. 18. Кривые пропускной способности для указанных экспериментов.
Что ж: разница хоть и не критическая, но есть!
Послесловие
Возможно, кто-то из читателей мог заметить, что почти всё, что мы рассмотрели сегодня (подробно и вскользь) весьма неплохо ложится на параметры матлабовского объекта comm.MIMOChannel. Мне этот факт кажется очень важным:
- во-первых, это дополнительно систематизирует выше описанное,
- а, во-вторых, подчеркивает то, что вопросы мы рассматриваем актуальные.
Ну, и теперь, если вы будете использовать подобные блоки, то, надеюсь, будет более понятным зачем и какие ручки нужно крутить.
Всех благодарю за внимание!
P.S.
Добавлю сюда ссылку на слайды по теме от Reiner S. Thomä (Ильменау), по которым он нам читал в своё время лекции. Думаю, кому-нибудь пригодится!
Литература
- Paulraj, Arogyaswami, Rohit Nabar, and Dhananjay Gore. Introduction to space-time wireless communications. Cambridge university press, 2003.
- Goldsmith A. Wireless communications. – Cambridge university press, 2005.
- Fontæn, Fernando Pærez, and Perfecto Mariæo Espiæeira. Modelling the wireless propagation channel: a simulation approach with Matlab. Vol. 5. John Wiley & Sons, 2008.
- Farrokhi, Farrokh R., et al. "Spectral efficiency of FDMA/TDMA wireless systems with transmit and receive antenna arrays." IEEE transactions on wireless communications 1.4 (2002): 591-599.