Предисловие
Данный текст будет являться одной из переписанных глав для учебного пособия по защите информации кафедры радиотехники и систем управления, а также, с этого учебного кода, кафедры защиты информации МФТИ (ГУ). Полностью учебник доступен на github (см. также draft releases). На Хабре планирую выкладывать новые «большие» куски, во-первых, чтобы собрать полезные комментарии и замечания, во-вторых, дать сообществу больше обзорного материала по полезным и интересным темам. Предыдущие разделы главы «Криптографически протоколы»: 1, 2, 3, 4
Схемы распределения ключей с доверенным центром состоят из трёх этапов.
- На первом этапе доверенный центр создаёт некоторый секрет, известный только ему. Это может быть некоторая секретная матрица с особыми свойствами, как в схеме Блома, или пара из закрытого и открытого ключей, как в схеме Жиро.
- Для каждого нового легального участника сети доверенный центр, используя свою секретную информацию, вырабатывает некоторый отпечаток или сертификат, который позволяет новому участнику вырабатывать сеансовые ключи с другими легальными участниками.
- Наконец, на третьем этапе, когда начинается протокол общения двух легальных участников, они предъявляют друг-другу идентификаторы и/или дополнительную информацию от доверенного центра. Используя её, без дополнительного обращения к центру, они могут сгенерировать секретный сеансовый ключ для общения между собой.
Схема Жиро
В схеме Жиро (фр. Marc Girault) надёжность строится на стойкости криптосистемы RSA (сложности факторизации больших чисел и вычисления дискретного корня).
Предварительно:
- Доверенный центр (Трент,
):
- выбирает общий модуль
, где
и
— большие простые числа;
- выбирает пару из закрытого и открытого ключей
и
;
- выбирает элемент
поля
максимального порядка;
- публикует в общедоступном месте параметры схемы
,
и
.
- выбирает общий модуль
- Каждый из легальных участников:
- выбирает себе закрытый ключ
и идентификатор
;
- вычисляет и отправляет доверенному центру
;
- используя протокол аутентификации сторон (см. ниже) легальный участник доказывает доверенному центру, что владеет закрытым ключом, не раскрывая его значение;
- получает от доверенного центр свой открытый ключ:
- выбирает себе закрытый ключ
В результате для каждого участника, например, Алисы, которая владеет
Протокол аутентификации сторон в общем случае выглядит следующим образом.
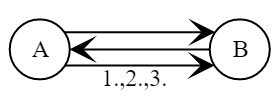
- Алиса выбирает случайное
.
- Боб выбирает случайное
.
- Боб вычисляет
;
Боб проверяет, что.
Протокол генерации сессионного ключа, либо просто схема Жиро, как и другие схемы, состоит из проходов обмена открытой информацией и вычисления ключа.
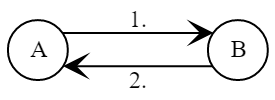
- Боб вычисляет
.
- Алиса вычисляет
.
В результате работы схемы стороны сгенерировали одинаковый общий сеансовый ключ.
Схема обеспечивает аутентификацию ключа (цель G7), так как только легальные пользователи смогут вычислить корректное значение общего сессионного ключа.
Схема Блома
Схема Блома (англ. Rolf Blom) используется в протоколе HDCP (англ. High-bandwidth Digital Content Protection) для предотвращения копирования высококачественного видеосигнала. Предполагается, что некоторый доверенный центр распределит ключи таким образом, что легальные производители видеокарт, мониторов высокого разрешения и других компонент будут передавать видеоконтент по защищённому каналу, а «пиратские» устройства не смогут эти данные перехватить, и, например, записать на другой носитель.
На этапе инициализации доверенный центр выбирает симметричную матрицу
Симметричность матрицы
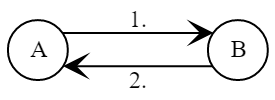
- Боб вычисляет
.
- Алиса вычисляет
.
Из симметричности матрицы
Присоединение новых участников к схеме строго контролируется доверенным центром, что позволяет защитить сеть от нелегальных пользователей. Надёжность данной схемы основывается на невозможности восстановить исходную матрицу. Однако для восстановления матрицы доверенного центра размера
Послесловие
Автор будет благодарен за фактические и другие замечания к тексту.