They say: ‘Brevity is the soul of wit’, so let’s get started.
Introduction
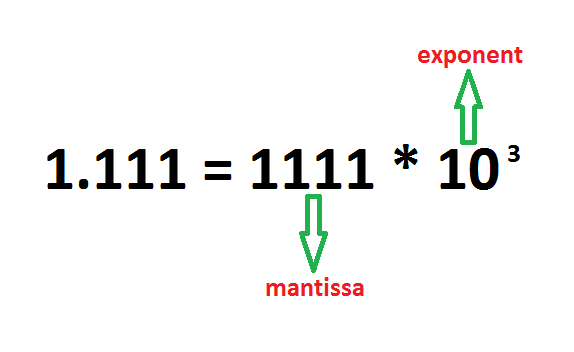
When I began to learn Python I came across a very curious subject, namely Real Numbers. It was about the mantissa, the exponent, and other details like the storage of bits in computers.
It turns out that computers operate integer numbers easily, but real numbers are more complicated.
Nature of the problem
Because of the essence of the floating — point numbers their processing has no absolute accuracy. It seemed to me nonsense that computers can’t compute precise values of ordinary two real numbers at least. How’s this possible? Yeah, actually, a computer programme isn’t able to add just two numbers without discrepancy.
Well, close enough you might say. Who cares about 17th decimal sign. But imagine you need to compute twenty numbers not two as in the example. Think about the error rises exponentially.
Tell me about libraries like a NumPy. They don’t solve the problem as well.
Solution
I came up with the solution following way:
Programme should operate with numbers as a human does. So deal only with integer numbers because we do the same in fact.
The idea is to make a function calculating like usual people.
Link GitHub
Conclusion
Accuracy is the most important thing in computation and it must be as accurate as possible not only on paper but in programmes too. Various fields need high precise: engineering, quantum physics, biology and others where even tiny inaccuracies are unacceptable.
Here’s some examples how the function works:
Yeah, sure, this algorithm don’t solve the whole problem in calculus and only works with positive numbers. But it solves at least one, but such an important problem as the most accurate addition of real numbers.
I hope on the example of this case people will know more how computers are inaccurate sometimes and how important to develop accurate computing is.
Sources:
Introduction
When I began to learn Python I came across a very curious subject, namely Real Numbers. It was about the mantissa, the exponent, and other details like the storage of bits in computers.

It turns out that computers operate integer numbers easily, but real numbers are more complicated.
Nature of the problem
Because of the essence of the floating — point numbers their processing has no absolute accuracy. It seemed to me nonsense that computers can’t compute precise values of ordinary two real numbers at least. How’s this possible? Yeah, actually, a computer programme isn’t able to add just two numbers without discrepancy.
x = 0.1
y = 0.2
print(x + y) # 0.30000000000000004 Well, close enough you might say. Who cares about 17th decimal sign. But imagine you need to compute twenty numbers not two as in the example. Think about the error rises exponentially.
Tell me about libraries like a NumPy. They don’t solve the problem as well.
Solution
I came up with the solution following way:
Programme should operate with numbers as a human does. So deal only with integer numbers because we do the same in fact.
The idea is to make a function calculating like usual people.
Link GitHub
Conclusion
Accuracy is the most important thing in computation and it must be as accurate as possible not only on paper but in programmes too. Various fields need high precise: engineering, quantum physics, biology and others where even tiny inaccuracies are unacceptable.
Here’s some examples how the function works:
plus_sum = plus(52.92, 20.99, 0.10)
print(float('{:.21f}'.format(plus_sum))) # 74.01
python_sum = 52.92 + 20.99 + 0.10
print(float('{:.21f}'.format(python_sum))) # 74.00999999999999
python_sum = 0.1 + 0.2
print(python_sum == 0.3) # False
plus_sum = plus(0.1, 0.2)
print(plus_sum == 0.3) # TrueYeah, sure, this algorithm don’t solve the whole problem in calculus and only works with positive numbers. But it solves at least one, but such an important problem as the most accurate addition of real numbers.
I hope on the example of this case people will know more how computers are inaccurate sometimes and how important to develop accurate computing is.
Sources: