Математика для искусственных нейронных сетей для новичков, часть 3 — градиентный спуск продолжение
6 min
Часть 2 — градиентный спуск начало
В предыдущей части я начал разбор алгоритма оптимизации под названием градиентный спуск. Предыдущая статья оборвалась на писании варианта алгоритма под названием пакетный градиентный спуск.
Существует и другая версия алгоритма — стохастический градиентный спуск. Стохастический = случайный.
В предыдущей части я начал разбор алгоритма оптимизации под названием градиентный спуск. Предыдущая статья оборвалась на писании варианта алгоритма под названием пакетный градиентный спуск.
Существует и другая версия алгоритма — стохастический градиентный спуск. Стохастический = случайный.
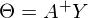 , где
, где 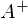 — псевдообратная матрица. Это решение наглядное, точное и короткое. Но есть проблема, которую можно решить численно. Градиентный спуск — метод численной оптимизации, который может быть использован во многих алгоритмах, где требуется найти экстремум функции — нейронные сети, SVM, k-средних, регрессии. Однако проще его воспринять в чистом виде (и проще модифицировать).
— псевдообратная матрица. Это решение наглядное, точное и короткое. Но есть проблема, которую можно решить численно. Градиентный спуск — метод численной оптимизации, который может быть использован во многих алгоритмах, где требуется найти экстремум функции — нейронные сети, SVM, k-средних, регрессии. Однако проще его воспринять в чистом виде (и проще модифицировать).