На Хабрахабре неоднократно обсуждался генетический алгоритм, его преимущества и недостатки. Но генетический алгоритм (а точнее целая плеяда различных его подвидов) не является единственным в своём роде. Его относят к так называемым естественным алгоритмам. К ним также принадлежат алгоритм «имитации отжига», алгоритм «поведения роя пчёл» и алгоритм «поведения колонии муравьёв» и ещё несколько почти неизвестных алгоритмов.
Я хотел бы остановиться на втором, менее популярном но не менее интересном алгоритме синтеза и оптимизации — алгоритме поведения роя пчёл — и объяснить его принцип.
Для рассмотрения принципов работы алгоритма поведения роя пчёл, или метода роя пчёл (МРП) прибегнем к аналогии с реальным роем пчел. Представим себе рой пчел на поле. Их цель – найти на поле область с наивысшей плотностью цветов. Без какого-либо представления о поле априори, пчелы начинают поиск цветов со случайных позиций со случайными векторами скорости. Каждая пчела может помнить позиции, где она нашла наибольшее количество цветов и каким-то образом знать области, где другие пчелы обнаружили наибольшую плотность цветов. Выбирая между возвращением к месту, где пчела сама обнаружила наибольшее количество цветов, или исследованием места, определенного другими, как место с наибольшим количеством цветов, пчела устремляется в направлении между двумя точками в зависимости от того, что окажет большее влияние на ее решение – персональное воспоминание или социальный рефлекс. По пути пчела может найти место с более высокой концентрацией цветов, чем было найдено ранее. В дальнейшем оно может быть обозначено как новое место с наибольшей концентрацией цветов, а также как место наибольшего скопления цветов, найденное всем роем. Случайно пчела может пролететь мимо места, с большим количеством цветов, чем было найдено любой другой пчелой роя. Весь рой, затем будет стремиться навстречу этому месту в дополнении к собственным наблюдениям каждой пчелы. Таким образом, пчелы исследуют поле: перелетая места с наибольшей концентрацией, они замедляются в их направлении. Непрерывно они проверяют места, которые пролетели, сравнивая с найденными ранее местами с наибольшей концентрацией цветов надеясь найти абсолютную наибольшую концентрацию цветов. В конечном итоге, пчела заканчивает движение на месте поля с наибольшей концентрацией цветов. Вскоре весь рой сосредотачивается в окрестностях этой позиции. Не имея возможности обнаружить места с большей концентрацией цветов, пчелы непрерывно роятся в районе наибольшей плотности цветов. Это поведение пчёл и было положено в основу этого метода оптимизации.
Частица или Агент – каждая пчела в рое рассматривается как частица или агент. Все частицы роя действуют индивидуально в соответствии с одним управляющим принципом: ускоряться в направлении наилучшей персональной и наилучшей общей позиции, постоянно проверяя значение текущей позиции.
Позиция – аналогично местоположению пчелы на поле представляется координатами на плоскости x-y. Однако, в общем случае можно расширить эту идею в любое N-мерное пространство в соответствии с поставленной задачей. Это N-мерное пространство является областью решений для оптимизируемой задачи, где каждый набор координат представляет решение.
Пригодность — по аналогии с примером пчелиного роя функция пригодности будет плотностью цветов: чем больше плотность, тем лучше позиция. Функция пригодности служит средством связи между физической проблемой и алгоритмом оптимизации.
Персональная наилучшая позиция – по аналогии с пчелиным роем, каждая пчела помнит позицию, где она сама обнаружила наибольшее количество цветов. Эта позиция с наибольшим значением пригодности обнаруженная пчелой известна как персональная наилучшая позиция (ПНП). Каждая пчела имеет собственное ПНП, определяемое путем, который она пролетела. В каждой точке вдоль пути движения пчела сравнивает значение пригодности текущей позиции со значением ПНП. Если текущая позиция имеет значение пригодности выше, значение ПНП заменяется на значение текущей позиции.
Глобальная наилучшая позиция – каждая пчела также каким-то образом узнает область наибольшей концентрации цветов, определенную всем роем. Эта позиция наибольшей пригодности известна как глобальная наилучшая позиция (ГНП). Для всего роя это одна ГНП, к которой стремится каждая пчела. В каждой точке на протяжении всего пути каждая пчела сравнивает пригодность ее текущей позиции с ГНП. В случае если какая-либо пчела обнаружит позицию с более высокой пригодностью, ГНП заменяется текущей позицией этой пчелы.
Первым шагом в реализации МРП является выбор параметров, которые необходимо оптимизировать, и определение допустимого интервала для поиска оптимальных значений. Затем в допустимой области случайным образом располагаются пчёл, а также задаются векторы и скорости их движения. Затем каждая частица должна перемещаться через пространство решений, как если бы она была пчелой в рое. Алгоритм действует на каждую частицу отдельно, перемещая ее на небольшую величину, циклично двигая ее через весь рой. Следующие шаги выполняются для каждой частицы:
Оценка пригодности для частицы, сравнение с ПНП и ГНП. Функция пригодности, используя координаты частицы в пространстве решений, возвращает значение пригодности для текущей позиции. Если это значение больше, чем значение ПНП, соответствующее этой частице, или ГНП, тогда соответствующие позиции заменяются текущей позицией.
Корректировка скорости частицы. Манипуляции со скоростью частицы являются основным элементом всей оптимизации. Точное понимание уравнения, используемого для определения скорости, является ключом к пониманию всего процесса оптимизации. Скорость частицы меняется в соответствии с взаимным расположением позиций ПНП и ГНП. Она стремится в направлении этих позиций наибольшей пригодности в соответствии со следующим уравнением
где:
— это скорость частицы в n-том измерении на предыдущем шаге,
— это координата частицы в n-том измерении,
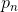— ПНП,
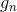— ГНП.
Расчет производится для каждого из N. Из этого уравнения видно, что новая скорость получается из старой скорости путем простого масштабирования на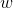
, и прибавления направления ГНП и ПНП для этого конкретного направления. 
и 
— это масштабные коэффициенты, которые определяют относительное взаимное «притяжение» к ПНП и ГНП. Они иногда рассматриваются как познавательный и социальный факторы. — это коэффициент, определяющий какое влияние на частицу оказывает ее память о ПНП, и — коэффициент, определяющий какое влияние на частицу оказывают остальные члены роя. Увеличение предполагает исследование пространства решений путем движения каждой частицы в направлении своего ПНП; увеличение предполагает исследование предполагаемого глобального максимума. Функция случайных чисел rand() возвращает число в интервале между -1 и 1. В общем случае два появления функции rand() представляет собой два различных вызова функции. Большинство реализаций используют две независимые случайные величины для стохастического изменения относительного притяжения ГНП и ПНП. Это введение случайного элемента в оптимизацию предназначено для моделирования незначительного непредсказуемого компонента реального поведения роя. 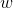называют «инерционным весом» и это число (выбранное в интервале между 0 и 1) отражает в какой мере частица остается верной своему первоначальному курсу, не подвергшемуся влиянию ГНП и ПНП.
Границы мы задали изначально, но нигде в формулах и методах о них не упоминалось. Так как же всё таки их учитывать? Существует несколько ответов на этот вопрос.
Например, можно сделать стены поглощающими. Когда частица ударяется об границу пространства решений в одном из измерений, скорость в этом измерении обнуляется, и частица в конечном итоге будет возвращена в заданное пространство решений. Это означает, что границы — «стены» поглощают энергию частиц, пытающихся разрешённую область. Или же отражать скорость частицы, когда та подлетает к «стене». Но самым эффективным решением оказались «невидимые стены». Частица может спокойно вылетать за их пределы, но находясь вне разрешённой области, значения, полученные ею значения просто не учитываются, до тех пор, пока она не вернётся обратно.
В итоге хочу заметить, что метод роя пчёл можно эффективно распределить на несколько параллельных процессов, за счёт чего значительно увеличится его скорость.
По сравнению с генетическим алгоритмом, операторы которого могут быть реализованы различным образом, имеет лишь один оператор — вычисление скорости, что делает его более простым в использовании.
В методе роя пчёл можно легко определить достижение точки глобального минимума, в то время как в генетических алгоритмах это значительно осложнено.
Концепция этих методов основывается на двух совершенно разных природных процессах: МРП основывается на социальном поведении роя, а генетический алгоритм имитирует процесс эволюции и естественного отбора. За счёт этого есть возможность объединить два этих метода.
Я хотел бы остановиться на втором, менее популярном но не менее интересном алгоритме синтеза и оптимизации — алгоритме поведения роя пчёл — и объяснить его принцип.
Для рассмотрения принципов работы алгоритма поведения роя пчёл, или метода роя пчёл (МРП) прибегнем к аналогии с реальным роем пчел. Представим себе рой пчел на поле. Их цель – найти на поле область с наивысшей плотностью цветов. Без какого-либо представления о поле априори, пчелы начинают поиск цветов со случайных позиций со случайными векторами скорости. Каждая пчела может помнить позиции, где она нашла наибольшее количество цветов и каким-то образом знать области, где другие пчелы обнаружили наибольшую плотность цветов. Выбирая между возвращением к месту, где пчела сама обнаружила наибольшее количество цветов, или исследованием места, определенного другими, как место с наибольшим количеством цветов, пчела устремляется в направлении между двумя точками в зависимости от того, что окажет большее влияние на ее решение – персональное воспоминание или социальный рефлекс. По пути пчела может найти место с более высокой концентрацией цветов, чем было найдено ранее. В дальнейшем оно может быть обозначено как новое место с наибольшей концентрацией цветов, а также как место наибольшего скопления цветов, найденное всем роем. Случайно пчела может пролететь мимо места, с большим количеством цветов, чем было найдено любой другой пчелой роя. Весь рой, затем будет стремиться навстречу этому месту в дополнении к собственным наблюдениям каждой пчелы. Таким образом, пчелы исследуют поле: перелетая места с наибольшей концентрацией, они замедляются в их направлении. Непрерывно они проверяют места, которые пролетели, сравнивая с найденными ранее местами с наибольшей концентрацией цветов надеясь найти абсолютную наибольшую концентрацию цветов. В конечном итоге, пчела заканчивает движение на месте поля с наибольшей концентрацией цветов. Вскоре весь рой сосредотачивается в окрестностях этой позиции. Не имея возможности обнаружить места с большей концентрацией цветов, пчелы непрерывно роятся в районе наибольшей плотности цветов. Это поведение пчёл и было положено в основу этого метода оптимизации.
Язык метода
Частица или Агент – каждая пчела в рое рассматривается как частица или агент. Все частицы роя действуют индивидуально в соответствии с одним управляющим принципом: ускоряться в направлении наилучшей персональной и наилучшей общей позиции, постоянно проверяя значение текущей позиции.
Позиция – аналогично местоположению пчелы на поле представляется координатами на плоскости x-y. Однако, в общем случае можно расширить эту идею в любое N-мерное пространство в соответствии с поставленной задачей. Это N-мерное пространство является областью решений для оптимизируемой задачи, где каждый набор координат представляет решение.
Пригодность — по аналогии с примером пчелиного роя функция пригодности будет плотностью цветов: чем больше плотность, тем лучше позиция. Функция пригодности служит средством связи между физической проблемой и алгоритмом оптимизации.
Персональная наилучшая позиция – по аналогии с пчелиным роем, каждая пчела помнит позицию, где она сама обнаружила наибольшее количество цветов. Эта позиция с наибольшим значением пригодности обнаруженная пчелой известна как персональная наилучшая позиция (ПНП). Каждая пчела имеет собственное ПНП, определяемое путем, который она пролетела. В каждой точке вдоль пути движения пчела сравнивает значение пригодности текущей позиции со значением ПНП. Если текущая позиция имеет значение пригодности выше, значение ПНП заменяется на значение текущей позиции.
Глобальная наилучшая позиция – каждая пчела также каким-то образом узнает область наибольшей концентрации цветов, определенную всем роем. Эта позиция наибольшей пригодности известна как глобальная наилучшая позиция (ГНП). Для всего роя это одна ГНП, к которой стремится каждая пчела. В каждой точке на протяжении всего пути каждая пчела сравнивает пригодность ее текущей позиции с ГНП. В случае если какая-либо пчела обнаружит позицию с более высокой пригодностью, ГНП заменяется текущей позицией этой пчелы.
Алгоритм
Первым шагом в реализации МРП является выбор параметров, которые необходимо оптимизировать, и определение допустимого интервала для поиска оптимальных значений. Затем в допустимой области случайным образом располагаются пчёл, а также задаются векторы и скорости их движения. Затем каждая частица должна перемещаться через пространство решений, как если бы она была пчелой в рое. Алгоритм действует на каждую частицу отдельно, перемещая ее на небольшую величину, циклично двигая ее через весь рой. Следующие шаги выполняются для каждой частицы:
Оценка пригодности для частицы, сравнение с ПНП и ГНП. Функция пригодности, используя координаты частицы в пространстве решений, возвращает значение пригодности для текущей позиции. Если это значение больше, чем значение ПНП, соответствующее этой частице, или ГНП, тогда соответствующие позиции заменяются текущей позицией.
Корректировка скорости частицы. Манипуляции со скоростью частицы являются основным элементом всей оптимизации. Точное понимание уравнения, используемого для определения скорости, является ключом к пониманию всего процесса оптимизации. Скорость частицы меняется в соответствии с взаимным расположением позиций ПНП и ГНП. Она стремится в направлении этих позиций наибольшей пригодности в соответствии со следующим уравнением
где:
— это скорость частицы в n-том измерении на предыдущем шаге, — это координата частицы в n-том измерении,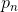 — ПНП, 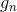— ГНП.Расчет производится для каждого из N. Из этого уравнения видно, что новая скорость получается из старой скорости путем простого масштабирования на
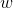, и прибавления направления ГНП и ПНП для этого конкретного направления. и — это масштабные коэффициенты, которые определяют относительное взаимное «притяжение» к ПНП и ГНП. Они иногда рассматриваются как познавательный и социальный факторы. — это коэффициент, определяющий какое влияние на частицу оказывает ее память о ПНП, и — коэффициент, определяющий какое влияние на частицу оказывают остальные члены роя. Увеличение предполагает исследование пространства решений путем движения каждой частицы в направлении своего ПНП; увеличение предполагает исследование предполагаемого глобального максимума. Функция случайных чисел rand() возвращает число в интервале между -1 и 1. В общем случае два появления функции rand() представляет собой два различных вызова функции. Большинство реализаций используют две независимые случайные величины для стохастического изменения относительного притяжения ГНП и ПНП. Это введение случайного элемента в оптимизацию предназначено для моделирования незначительного непредсказуемого компонента реального поведения роя. 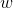называют «инерционным весом» и это число (выбранное в интервале между 0 и 1) отражает в какой мере частица остается верной своему первоначальному курсу, не подвергшемуся влиянию ГНП и ПНП.Граничные условия
Границы мы задали изначально, но нигде в формулах и методах о них не упоминалось. Так как же всё таки их учитывать? Существует несколько ответов на этот вопрос.
Например, можно сделать стены поглощающими. Когда частица ударяется об границу пространства решений в одном из измерений, скорость в этом измерении обнуляется, и частица в конечном итоге будет возвращена в заданное пространство решений. Это означает, что границы — «стены» поглощают энергию частиц, пытающихся разрешённую область. Или же отражать скорость частицы, когда та подлетает к «стене». Но самым эффективным решением оказались «невидимые стены». Частица может спокойно вылетать за их пределы, но находясь вне разрешённой области, значения, полученные ею значения просто не учитываются, до тех пор, пока она не вернётся обратно.
Заключение
В итоге хочу заметить, что метод роя пчёл можно эффективно распределить на несколько параллельных процессов, за счёт чего значительно увеличится его скорость.
По сравнению с генетическим алгоритмом, операторы которого могут быть реализованы различным образом, имеет лишь один оператор — вычисление скорости, что делает его более простым в использовании.
В методе роя пчёл можно легко определить достижение точки глобального минимума, в то время как в генетических алгоритмах это значительно осложнено.
Концепция этих методов основывается на двух совершенно разных природных процессах: МРП основывается на социальном поведении роя, а генетический алгоритм имитирует процесс эволюции и естественного отбора. За счёт этого есть возможность объединить два этих метода.
