В свете недавних статей об обработке изображений я хотел бы немного рассказать об алгоритмах выделения контуров: методы Робертса, Превитта и Собеля (эти методы взяты для рассмотрения как самые известные и часто используемые).
Не буду докучать объемной теорией, а ограничусь лишь минимальными сведениями, необходимыми для понимания сути алгоритмов.
Все указанные методы основываются на одном из базовых свойств сигнала яркости – разрывности. Наиболее общим способом поиска разрывов является обработка изображения с помощью скользящей маски, называемой также фильтром, ядром, окном или шаблоном, которая представляет собой некую квадратную матрицу, соответствующую указанной группе пикселей исходного изображения. Элементы матрицы принято называть коэффициентами. Оперирование такой матрицей в каких-либо локальных преобразованиях называется фильтрацией или пространственной фильтрацией.
Схема пространственной фильтрации иллюстрируется на рисунке ниже (см. рисунок 1).
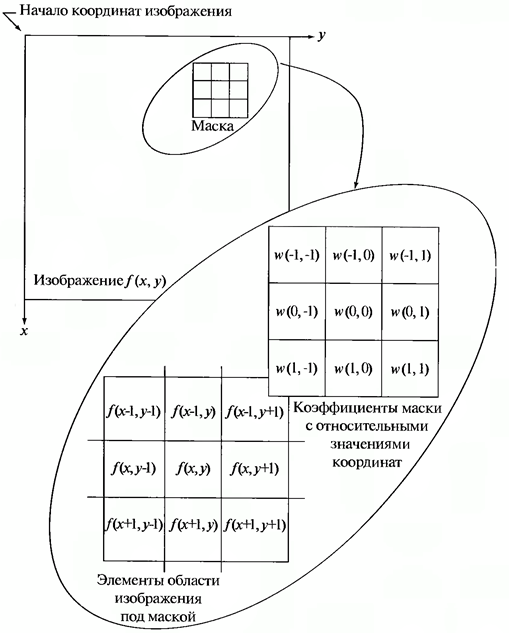
Рисунок 1. Схема пространственной фильтрации
Процесс основан на простом перемещении маски фильтра от точки к точке изображения; в каждой точке (x,y) отклик фильтра вычисляется с использованием предварительно заданных связей. В случае линейной пространственной фильтрации отклик задается суммой произведения коэффициентов фильтра на соответствующие значения пикселей в области, покрытой маской фильтра. Для маски 3х3 элемента, показанной на рисунке 1, результат (отклик) R линейной фильтрации в точке (x,y) изображения составит:
(1.1)
что, как видно, есть сумма произведений коэффициентов маски на значения пикселей непосредственно под маской. В частности заметим, что коэффициент w(0,0) стоит при значении f(x,y), указывая тем самым, что маска центрирована в точке (x,y).
При обнаружении перепадов яркости используются дискретные аналоги производных первого и второго порядка. Для простоты изложения будут рассмотрены одномерные производные.
Первая производная одномерной функции f(x) определяется как разность значений соседних элементов:
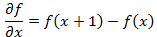(1.2)
Здесь использована запись в виде частной производной для того, чтобы сохранить те же обозначения в случае двух переменных f(x,y), где придется иметь дело с частными производными по двум пространственным осям. Использование частной производной не меняет существа рассмотрения.
Аналогично, вторая производная определяется как разность соседних значений первой производной:
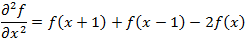(1.3)
Вычисление первой производной цифрового изображения основано на различных дискретных приближениях двумерного градиента. По определению, градиент изображения f(x,y) в точке (x,y) — это вектор [2]:
(1.4)
Как известно из курса математического анализа, направление вектора градиента совпадает с направлением максимальной скорости изменения функции f в точке (x,y) [2].
Важную роль при обнаружении контуров играет модуль этого вектора, который обозначается ∇f и равен
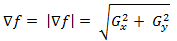(1.5)
Эта величина равна значению максимальной скорости изменения функции f в точке (x,y), причем максимум достигается в направлении вектора ∇f. Величину ∇f также часто называют градиентом.
Направление вектора градиента также является важной характеристикой. Обозначим α(x,y) угол между направлением вектора ∇f в точке (x,y) и осью x. Как известно из математического анализа [2],
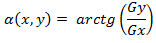(1.6)
Отсюда легко найти направление контура в точке (x,y), которое перпендикулярно направлению вектора градиента в этой точке. А вычислить градиент изображения можно, вычислив величины частных производных ∂f/∂x и ∂f/∂y для каждой точки.
Пусть область 3х3, показанная на рисунке ниже (см. рис. 2), представляет собой значения яркости в окрестности некоторого элемента изображения.
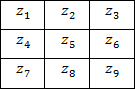
Рисунок 2. Окрестность 3х3 внутри изображения
Один из простейших способов нахождения первых частных производных в точке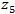
состоит в применении следующего перекрестного градиентного оператора Робертса [1]:
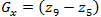(1.7)
и
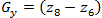(1.8)
Эти производные могут быть реализованы путем обработки всего изображения с помощью оператора, описываемого масками на рисунке 3, используя процедуру фильтрации, описанную ранее.
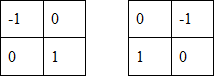
Рисунок 3. Маски оператора Робертса
Реализация масок размерами 2х2 не очень удобна, т.к. у них нет четко выраженного центрального элемента, что существенно отражается на результате выполнения фильтрации. Но этот «минус» порождает очень полезное свойство данного алгоритма – высокую скорость обработки изображения.
Оператор Превитта, так же как и оператор Робертса, оперирует с областью изображения 3х3, представленной на рисунке 2, только использование такой маски задается другими выражениями:
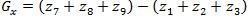(1.9)
и
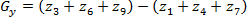(1.10)
В этих формулах разность между суммами по верхней и нижней строкам окрестности 3х3 является приближенным значением производной по оси x, а разность между суммами по первому и последнему столбцам этой окрестности – производной по оси y. Для реализации этих формул используется оператор, описываемый масками на рисунке 4, который называется оператором Превитта.
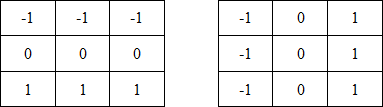
Рисунок 4. Маски оператора Превитта
Оператор Собеля тоже использует область изображения 3х3, отображенную на рисунке 2. Он довольно похож на оператор Превитта, а видоизменение заключается в использовании весового коэффициента 2 для средних элементов:
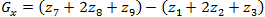(1.11)
и
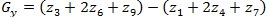(1.12)
Это увеличенное значение используется для уменьшения эффекта сглаживания за счет придания большего веса средним точкам.
Маски, используемые оператором Собеля, отображены на рисунке ниже (см. рис. 5).
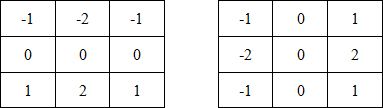
Рисунок 5. Маски оператора Собеля
Рассмотренные выше маски применяются для получения составляющих градиента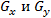
. Для вычисления величины градиента эти составляющие необходимо использовать совместно:
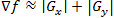(1.14)
или
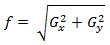(1.15)
Ну и в завершении продемонстрирую результаты обработки изображений (см. рисунки 6-8) описанными методами.
Рисунок 6. Исходное изображение №1
Рисунок 7. Исходное изображение №2
Рисунок 8. Исходное изображение №3
Результаты обработки методами Робертса, Превитта и Собеля продемонстрированы ниже:
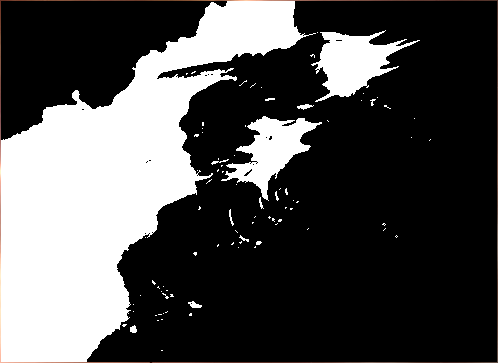
Рисунок 9. Исходные изображения после обработки методом Робертса
Рисунок 10. Исходные изображения после обработки методом Превитта
Рисунок 11. Исходные изображения после обработки методом Собеля
Не буду докучать объемной теорией, а ограничусь лишь минимальными сведениями, необходимыми для понимания сути алгоритмов.
Все указанные методы основываются на одном из базовых свойств сигнала яркости – разрывности. Наиболее общим способом поиска разрывов является обработка изображения с помощью скользящей маски, называемой также фильтром, ядром, окном или шаблоном, которая представляет собой некую квадратную матрицу, соответствующую указанной группе пикселей исходного изображения. Элементы матрицы принято называть коэффициентами. Оперирование такой матрицей в каких-либо локальных преобразованиях называется фильтрацией или пространственной фильтрацией.
Схема пространственной фильтрации иллюстрируется на рисунке ниже (см. рисунок 1).
Рисунок 1. Схема пространственной фильтрации
Процесс основан на простом перемещении маски фильтра от точки к точке изображения; в каждой точке (x,y) отклик фильтра вычисляется с использованием предварительно заданных связей. В случае линейной пространственной фильтрации отклик задается суммой произведения коэффициентов фильтра на соответствующие значения пикселей в области, покрытой маской фильтра. Для маски 3х3 элемента, показанной на рисунке 1, результат (отклик) R линейной фильтрации в точке (x,y) изображения составит:
(1.1)что, как видно, есть сумма произведений коэффициентов маски на значения пикселей непосредственно под маской. В частности заметим, что коэффициент w(0,0) стоит при значении f(x,y), указывая тем самым, что маска центрирована в точке (x,y).
При обнаружении перепадов яркости используются дискретные аналоги производных первого и второго порядка. Для простоты изложения будут рассмотрены одномерные производные.
Первая производная одномерной функции f(x) определяется как разность значений соседних элементов:
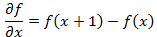(1.2)Здесь использована запись в виде частной производной для того, чтобы сохранить те же обозначения в случае двух переменных f(x,y), где придется иметь дело с частными производными по двум пространственным осям. Использование частной производной не меняет существа рассмотрения.
Аналогично, вторая производная определяется как разность соседних значений первой производной:
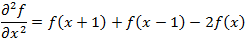(1.3)Вычисление первой производной цифрового изображения основано на различных дискретных приближениях двумерного градиента. По определению, градиент изображения f(x,y) в точке (x,y) — это вектор [2]:
(1.4)Как известно из курса математического анализа, направление вектора градиента совпадает с направлением максимальной скорости изменения функции f в точке (x,y) [2].
Важную роль при обнаружении контуров играет модуль этого вектора, который обозначается ∇f и равен
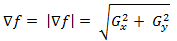(1.5)Эта величина равна значению максимальной скорости изменения функции f в точке (x,y), причем максимум достигается в направлении вектора ∇f. Величину ∇f также часто называют градиентом.
Направление вектора градиента также является важной характеристикой. Обозначим α(x,y) угол между направлением вектора ∇f в точке (x,y) и осью x. Как известно из математического анализа [2],
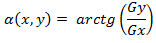(1.6)Отсюда легко найти направление контура в точке (x,y), которое перпендикулярно направлению вектора градиента в этой точке. А вычислить градиент изображения можно, вычислив величины частных производных ∂f/∂x и ∂f/∂y для каждой точки.
Оператор Робертса
Пусть область 3х3, показанная на рисунке ниже (см. рис. 2), представляет собой значения яркости в окрестности некоторого элемента изображения.
Рисунок 2. Окрестность 3х3 внутри изображения
Один из простейших способов нахождения первых частных производных в точке
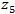состоит в применении следующего перекрестного градиентного оператора Робертса [1]:
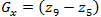(1.7)и
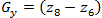(1.8)Эти производные могут быть реализованы путем обработки всего изображения с помощью оператора, описываемого масками на рисунке 3, используя процедуру фильтрации, описанную ранее.
Рисунок 3. Маски оператора Робертса
Реализация масок размерами 2х2 не очень удобна, т.к. у них нет четко выраженного центрального элемента, что существенно отражается на результате выполнения фильтрации. Но этот «минус» порождает очень полезное свойство данного алгоритма – высокую скорость обработки изображения.
Оператор Превитта
Оператор Превитта, так же как и оператор Робертса, оперирует с областью изображения 3х3, представленной на рисунке 2, только использование такой маски задается другими выражениями:
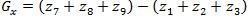(1.9)и
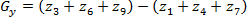(1.10)В этих формулах разность между суммами по верхней и нижней строкам окрестности 3х3 является приближенным значением производной по оси x, а разность между суммами по первому и последнему столбцам этой окрестности – производной по оси y. Для реализации этих формул используется оператор, описываемый масками на рисунке 4, который называется оператором Превитта.
Рисунок 4. Маски оператора Превитта
Оператор Собеля
Оператор Собеля тоже использует область изображения 3х3, отображенную на рисунке 2. Он довольно похож на оператор Превитта, а видоизменение заключается в использовании весового коэффициента 2 для средних элементов:
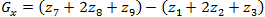(1.11)и
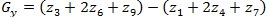(1.12)Это увеличенное значение используется для уменьшения эффекта сглаживания за счет придания большего веса средним точкам.
Маски, используемые оператором Собеля, отображены на рисунке ниже (см. рис. 5).
Рисунок 5. Маски оператора Собеля
Рассмотренные выше маски применяются для получения составляющих градиента
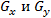. Для вычисления величины градиента эти составляющие необходимо использовать совместно:
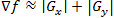(1.14)или
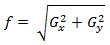(1.15)Ну и в завершении продемонстрирую результаты обработки изображений (см. рисунки 6-8) описанными методами.
Рисунок 6. Исходное изображение №1
Рисунок 7. Исходное изображение №2
Рисунок 8. Исходное изображение №3
Результаты обработки методами Робертса, Превитта и Собеля продемонстрированы ниже:
Рисунок 9. Исходные изображения после обработки методом Робертса
Рисунок 10. Исходные изображения после обработки методом Превитта
Рисунок 11. Исходные изображения после обработки методом Собеля
Список литературы
- Р. Гонсалес, Р. Вудс Цифровая обработка изображений — М: Техносфера, 2005 – 1007с
- Кудрявцев Л.В. Краткий курс математического анализа – M.: Наука, 1989 – 736с
- Анисимов Б.В. Распознавание и цифровая обработка изображений – М.: Высш. школа, 1983 – 295с
