РАМ-машина — абстрактная вычислительная машина, обладающая полнотой по Тьюрингу, и принадлежащая классу регистровых машин. Она эквивалентна универсальной машине Тьюринга, при этом более наглядна и удобна в доказательстве корректности алгоритмов. В этом топике я расскажу, как она устроена и приложу ссылки на работающую имплементацию эмулятора РАМ-машины с некоторыми интересными примерами.
Абстрактная модель РАМ-машины (RAM: Random Access Machine) предполагает наличие бесконечного набора регистров, каждый из которых способен хранить целое число любой длины. Индекс регистра может быть любым целым числом (в т.ч. отрицательным). Программа для РАМ-машины — конечный набор инструкций, модифицирующих регистры памяти; можно смотреть на это как на очень простой ассемблер. Изучение машины начнем с рассмотрения набора команд.
HALT
Самая простая инструкция, приказывающая машине остановить выполнение по ее достижению.
READ
Машина должна поддерживать ввод-вывод, и операция READ предназначена для ввода числа с клавиатуры (или другого потока, однако, не стоит забывать что мы имеем дело с абстрактной моделью, где главное обеспечить ввод данных для алгоритма, чтобы можно было решить массовую задачу). Число вводится в регистр
[0], этот регистр и дальше будем считать «особенным».WRITE
Выводит (на экран) число, хранящееся в
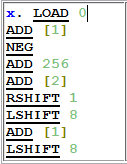
[0]. Больше никаких аргументов.LOAD x / [x] / [[x]]
Более хитрая инструкция — записывает в
[0] произвольное значение. Значение может быть задано константно: LOAD 5, например. Или скопировано из другой ячейки: LOAD [3] — здесь значение из третьего регистра копируется в нулевой. Или же с помощью двойной адресации: LOAD [[3]] — в «ноль» попадет число из регистра, на который «ссылается» третий регистр. Таким образом, видно, что машина поддерживает косвенную адресацию.STORE [x] / [[x]]
Записывает значение из
[0] в заданную ячейку. Доступна либо прямая адресация: STORE [1], либо косвенная: STORE [[1]].NEG
Обращает знак числа в
[0]. Соответственно -3 будет заменено на 3, ноль знака не имеет.LSHIFT x / [x] / [[x]]
Выполняет побитовый сдвиг влево числа в
[0] на указанный аргумент; доступна константа, прямой адрес, косвенный адрес. Например LSHFIT [[3]] умножит значение в [0] на двойку в степени значения регистра, на который ссылается [3].RSHIFT x / [x] / [[x]]
Выполняет побитовый правый сдвиг, аргументы и смысл аналогичны LSHIFT. Классическая модель не допускает использование знаковых чисел в качестве аргументов LSHIFT/RSHIFT.
ADD x / [x] / [[x]]
Прибавляет к
[0] значение, указанное аргументом функции. Доступна константа, прямая адресация, косвенная.Ну и напоследок, пригодится для организации циклов и условий:
JUMP метка
Безусловный переход на указанную строку кода или метку.
JG метка
Переход на указанную метку, если значение в нулевом регистре строго положительное.
Вот и все!
А как же другие арифметические операции? Да, классическая модель не предполагает избыточных инструкций, поэтому их придется реализовывать через сложение. В качестве небольшой головоломки предлагаю реализовать:
- умножение m на n (быстрее чем за O(max(m,n)));
- квадрат m (быстрее чем за O(m));
- степень m (быстрее чем за O(m * log(m)));
- корень произвольной степени (вспомнить метод Ньютона).
Более сложной задачей можно считать доказательство оценки сложности и корректности реализации каждого метода (но здесь это куда проще, чем на машине Тьюринга).
Одним из простейших свойств машины является легкость обнаружения deadlock-состояния (стабильного бесполезного состояния): если при переходе к той же метке значения регистров остались прежними — то мы «зависли».
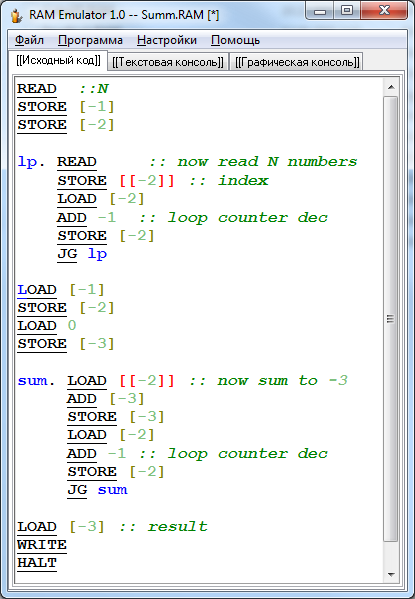
Прилагаю пример простейшей программы (надеюсь, самоочевидной), которая суммирует N чисел введенных с клавиатуры (другие примеры в архиве с исполняемым файлом эмулятора):
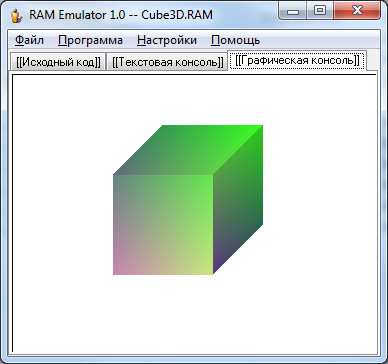
Для некоторого разнообразия (если честно, изначально, чтобы «повеселить» детишек в школе) я добавил несколько примитивов (точка и линия) для рисования графических элементов, которыми можно создать что-нибудь забавное. Например:
Скачать имплементацию можно по этой ссылке, а исходники — здесь. К качеству исходников, как и к языку, на котором они написаны (да, это Delphi) не стоит сильно придираться, я их писал уже много лет назад и сам удивлен, что все работает. Реализация поддерживает длинную арифметику и эмулирует бесконечное число регистров, однако мы знаем, что память физической машины не безгранична :)
Удачи в попытках!
