Здравствуйте, уважаемое сообщество! Думаю, многим знакома такая структура данных как суффиксное дерево. На Хабре уже было описание как его построить и зачем. Если вкратце, то оно нужно тогда, когда надо много раз искать какие-то произвольные образцы Xi в заранее заданном тексте A, а строится такое дерево мучительно с помощью алгоритма Укконена (есть и другие варианты, но они предполагают еще большее количество страданий). Общее наблюдение при работе с алгоритмами таково, что деревья — это, конечно, хорошо, но на практике их лучше избегать из за серьезных оверхэдов по памяти и не очень оптимального (с точки зрения эффективности оперирования данными компьютером) расположения. Кроме того, именно в таком дереве есть еще более существенная неприятность, а именно алфавитнозависимость структуры. Для решения этих проблем был придуман суффиксный массив. О том как его строить и как использовать и пойдет в этой статье.
Материал статьи предполагает знание понятий суффикса и префикса строки, а также знание того, как работает бинарный поиск. Надо также представлять, что такое стабильная сортировка и поразрядная сортировка, а также понимание, что имеется ввиду под стабильной сортировкой подсчетом. Для некоторых частей нам понадобится знание задачи о минимуме на отрезке — Range Minimum Query (RMQ). Ну, в общем, вас предупредили: никто не говорил, что будет просто.
Итак, чем же не устраивает нас дерево? Во-первых, это конечно то, что из за необходимости хранить ссылки на детей, родителя и т.п. размер используемой памяти в этом случае заметно больше, чем если эти ссылки не хранить. Во-вторых, если аллоцировать память под данные каким-нибудь стандартным аллокатором, то их «раскидает по разным углам», в результате обход дерева будет предполагать большое количество переходов в памяти, что плохо сказывается на на работе кэша памяти. Конечно есть уловки, которые позволяют эту проблему подавить: надо размещать узлы дерева в массиве, а вместо указателей использовать индекс в массиве. Тогда дерево будет представляться цельным куском памяти.
Ну это общие проблемы для всех деревьев. А что там с пресловутой алфавитной зависимостью? Посмотрим на практическую реализацию суффиксного дерева (если вы не сталкивались с ним, то для понимания сути проблемы это не важно). В каждом узле такого дерева могут быть ссылки на детей в количестве от 1 (например для терминальной вершины без ветвления) и до размера алфавита. Вот и возникает вопрос как хранить эти ссылки. Можно, например, в каждом узле держать массив ссылок размером с алфавит. Работать это будет быстро — узнать, есть ли соответствующий ребенок в данном узле можно за O(1). Но в большинстве ячеек массива будут храниться нулевые ссылки, а память на эти ячейки уйдет. Для небольших алфавитов (например, нуклеотиды в ДНК) черт с ним, но представьте себе китайские иероглифы? В принципе далеко ходить не надо: даже не case-sensitive русский алфавит заставляет призадуматься, а хотим ли мы столько пустых данных иметь.
Можно экономней расходовать память, помещая в некий динамически-изменяемый массив (вектор) только непустые ссылки, но тогда уже проверка наличия соответствующего ребенка узла за O(1) становится весьма сомнительной. Если хранить ссылки в отсортированном виде, то O(log(размер алфавита)). Можно попробовать поиграть с хэш-таблицами, но это будет иметь смысл только для сверхбольших алфавитов, и к тому же вводится еще один уровень косвенности. Да и строить такие деревья уже не O(n). В общем, в любом случае надо будет идти на какой-то компромисс между памятью и производительностью.
В 1989 году Манбер и Майерс опубликовали статью, в которой описали такую структуру данных, как суффиксный массив, и как ее применять для поиска подстрок. Суффиксный массив — это массив лексикографически отсортированных суффиксов строк (если терминология незнакома, то можно глянуть раздел «постановка задачи» в этой статье). Вообще говоря, хранить сами суффиксы смысла нет, достаточно хранить позицию начала данного суффикса, но определение массива так легче воспринимается. Вот пример для строки «mississippi»:
Также важное понятие ранг суффикса — то место, которое займет суффикс при сортировке, то есть его позиция в суффиксном массиве. Это взаимнообратные величины. Мы не будем их особо как-то различать, так как имея один массив, получить другой можно за O(N), так что можно всегда иметь под рукой оба.
Рассмотрим пример. Исходная строка «mississippi». Допустим, приходит к нам образец «sip». Простейший способ узнать, встречается ли образец в тексте, используя суффиксный массив, это взять первый символ образца и бинарным поиском (массив у нас отсортирован) найти диапазон с суффиксами, начинающимися на такую же букву. Так как все элементы в диапазоне отсортированы, а первые символы одинаковые, то оставшиеся после отбрасывания первого символа суффиксы тоже отсортированы. А значит, можно повторять процедуру сужения диапазона поиска до получения либо пустого диапазона, либо успешного нахождения всех символов образца. Очевидно, что таким образом за O(|X|log|A|) операций мы получим ответ.
Точно такую же сложность получим, если будем применять бинарный поиск «в лоб»: с полными лексикографическими сравнениями строк по краям и в медиане с образцом: O(log|A|) сравнений со средней «ценой» сравнения O(|X|).
Неплохо, но можно лучше. На самом деле не обязательно сравнивать всю искомую строку с элементом массива. На каждой итерации бинарного поиска мы уточняем некий диапазон, внутри которого может находиться искомый элемент. Все строки в таком диапазоне в некотором смысле похожи. А именно, у данных строк может быть общий префикс с искомой строкой, так как у тех, что остались вне диапазона, общего префикса уж точно не будет (в том смысле, что мы не рассматриваем уже обработанную часть образца как часть префикса).
Допустим, мы знаем длину общего префикса оставшегося образца с краями текущего диапазона l=lcp(X,S[L]) и r=lcp(X,S[R]) для левого и правого края (lcp — longest common prefix). Первое утверждение заключается в том, что для любой строки внутри диапазона lcp не меньше, чем минимум этих двух чисел. Если бы это было не так, то значит при неизменной начальной части префикса была бы позиция, где символ сначала совпадал бы с соответствующим символом образца, потом не совпадал, а потом снова совпадал. Это противоречило бы отсортированности диапазона. Важно хорошо проникнуться этой идеей, так как дальше мы ее будем использовать как нечто само собой разумеющееся. Второе утверждение очевидно: если общий префикс образца и любой строки внутри диапазона не меньше m=min(l,r), то m символов можно пропускать сразу, зная, что они совпадают в любом случае, и сравнивать только начиная с m+1 (и получая в результате lcp для данной строки).
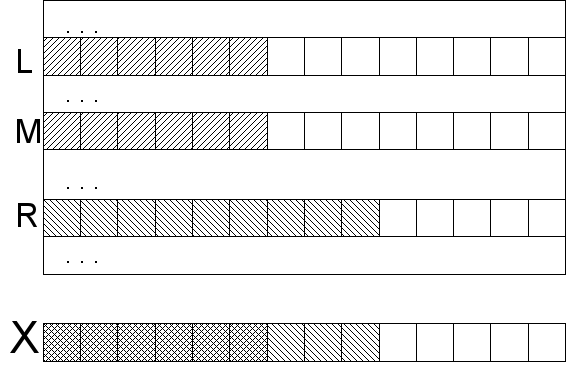
Таким образом мы применим оптимизированное сравнение строк в бинарном поиске строки «в лоб». В худшем случае, конечно, ничего мы от этого не выиграем: если искомый элемент находится на краю массива, но соседи совсем не похожи по lcp, то r (или l) будет мало каждый раз, m будет тоже мало, а значит придется проверять каждый символ по log|A| раз. Но экспериментальные наблюдения свидетельствуют, что для естественных текстов время поиска существенно сокращается по сравнению с O(log|A||X|), хотя про какую-то конкретную асимптотику утверждать что либо сложно.
В принципе, для практических применений этого уже вполне достаточно, но если хочется выжать все, то…
Это не предел. Позиции краев участка массива задают центр этого участка, и все такие конфигурации, которые реализуются при бинарном поиске являются подмножеством фиксированного набора размера |A|-2. Допустим мы заранее позаботились посчитать в этих конфигурациях величины ml=lcp(S[M],S[L]) и mr=lcp(S[M],S[R]), где M — середина участка между L и R, в которую мы пойдем на шаге бинарного поиска.
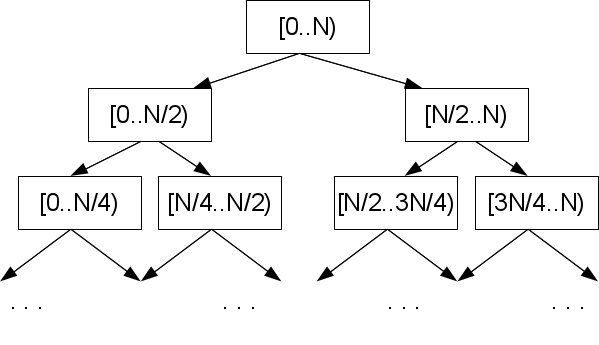
Посмотрим на один из краев, скажем, левый. Если посчитанный нами l<ml, то значит левый край похож на середину (и на любой элемент между ними) гораздо сильнее, чем нам хотелось бы, и значит результат сравнения заранее известен для всего участка между L и M: lcp(X,S[M])=l. Из этого непосредственно ясно, что искомый элемент точно не на этом участке, и если и искать его, то в противоположной половине. Если же l>ml, то значит середина похожа на левый край меньше, чем искомый образец. Значит lcp(X,S[M])=ml, а искомый элемент следует искать где-то между ними.
Естественно, ничего не меняется в рассуждениях, если заменить левый край на правый. Не рассмотренным оказался только один случай: l=ml и r=mr (если хоть одно равенство не верно, то результат известен согласно предыдущему абзацу). Тогда ясно, что lcp(X,S[M]) не меньше max(l,r), но для его точного определения и выяснения в какую сторону идти надо будет сравнивать символы (наконец то!) начиная с позиции max(l,r)+1.
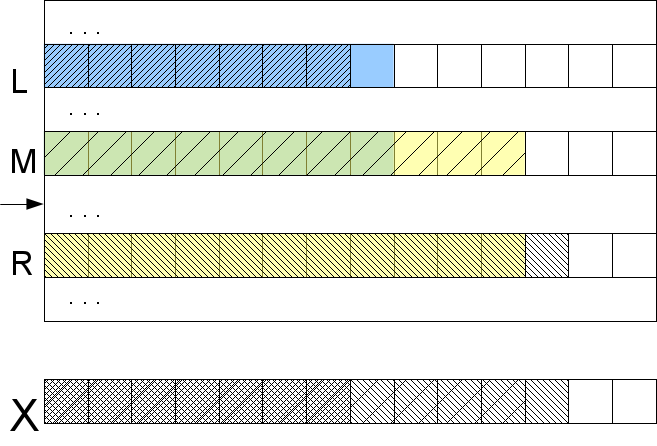
Что же у нас получилось? Часть шагов бинарного поиска мы сделаем сравнивая несколько lcp между собой, а если уж и дойдет до сравнения символов, то не более одного раза на символ X (мы берем max(l,r)+1, а значит никогда не возвращаемся назад). Таким образом получаем сложность алгоритма O(log|A| + |X|) в худшем случае. Правда, нужны предпосчитаные lcp для суффиксов текста A, встречающихся в дереве поиска, индуцированного алгоритмом бинарного поиска.
Важно отметить, что если мы не будем знать mr, а только ml, то тоже ничего страшного. Мы лишаемся возможности заранее сказать, что вхождение отсутствует, но сложность это не ухудшает: просто не будем смотреть на правый край, только левый. Если l<ml, то ищем дальше в другой половине, а l сохраняется, если l>ml, то r берем как ml и ищем в этой половине, ну а если l=ml, то сравниваем медианный элемент с искомой строкой начиная с l+1-ой позиции. Назад мы не возвращаемся и в этом случае тоже, а значит можно обойтись lcp только для левых краев без ухудшения сложности алгоритма.
Как вы помните, для эффективного поиска подстрок нам нужны были предпосчитаные lcp для определенных комбинаций суффиксов. Надо объяснить как их получать. Способы обычно сводятся к задаче о поиске минимума на отрезке — RMQ, поэтому алгоритмическая сложность алгоритма по большей части обусловлена тем, насколько эффективно вы умеете решать задачу RMQ. Более-менее простой алгоритм обойдется в O(NlogN) на предобработке и O(1) на запрос. То есть если вы используете построение суффиксного массива за O(NlogN), то вполне можно использовать его. Разумеется, если вы хотите строить суффиксный массив за линейное время, то придется применять алгоритм предобработки RMQ за линейное время с константными запросами.
Сначала построим так называемый lcp-массив — это массив значений lcp между лексикографически-соседними суффиксами (после того, как у нас построен суффиксный массив, какие суффиксы у нас соседние вопросов не вызывает). Если у нас есть lcp-массив, то нахождение lcp между двумя элементами сводится к поиску минимального значения на заданном отрезке lcp-массива, то есть задача RMQ — поиск минимума на отрезке — в чистом виде. Почему это так, понятно из соображений упорядоченности суффиксов: если бы lcp между двумя строками был больше, то все строки между ними тоже бы содержали как минимум такое же количество одинаковых символов в начале, и все lcp между этими строками были бы не меньше взаимного lcp крайних элементов.
Построить массив lcp достаточно просто. Конечно, идти по суффиксному массиву и считать lcp соседних элементов не получится — это O(N2). Но если идти по массиву в правильном порядке, то можно использовать информацию с предыдущего шага для расчетов. А именно, если перебирать суффиксы в том порядке, в котором они встречаются в исходной строке, то на каждом шаге lcp по сравнению с предыдущем шагом не может уменьшиться больше чем на 1, то есть может быть больше, может не измениться, но если уж станет меньше, то только на 1. Это происходит по следующей причине. Если вы выяснили, что lcp(A[i..],A[j..])=l, то отбрасывание первого символа, очевидно, уменьшает его на единицу: lcp(A[i+1..],A[j+1..])=l-1. Конечно, если i-ый и j-ый суффиксы оказались лексикографически соседними, то это не гарантирует, что i+1-ый и j+1-ый будут соседними — между ними, скорее всего, вклинятся другие. Но, как мы уже выяснили, lcp между ними — это минимальное lcp на всем отрезке между ними, а значит lcp между i+1-м суффиксом и лексикографически следующим за ним не меньше l-1.
Это позволяет пропустить все символы до предпоследнего (l-1), так как мы уверены, что они равны, и сравнивать только l-ый символ и далее. Значит, любые сделанные нами проверки либо увеличивают текущее lcp, либо заставляют нас переходить к следующей итерации. Таким образом пройдя все суффиксы кроме лексикографически последнего (его надо пропустить) мы получим lcp-массив за линейное время O(N).
Ну вот и все. Осталось найти RMQ для необходимых нам пар суффиксов. Решение RMQ состоит из предобработки и, собственно, ответов на запросы минимума между элементами. Так как основная вычислительная нагрузка приходится на предобработку, а выполнение запросов можно сделать O(1), то вообще говоря необязательно выписывать в явном виде интересующие нас пары и lcp между ними, так как за O(1) мы можем ответить об lcp произвольной пары суффиксов, в том числе и тех, которые играют роль в бинарном поиске. Учитывая, что это нас избавляет от необходимости думать как адресоваться к сохраненным значениям, это очень здорово. Если все-таки хочется хранить lcp в уже посчитанном виде, то надо правильно пронумеровать состояния в дереве поиска — почитайте про расположение в памяти и адресацию в бинарной куче.
Про то, как решать RMQ я писать не буду — на Хабре уже была хорошая статья про простой вариант за O(NlogN), и, надеюсь, будет продолжение, в котором напишут про хардкорный вариант за O(N) — алгоритм Фараха-Колтона и Бендера.
Замечательно, вот мы знаем как применить суффиксный массив, но откуда он у нас возьмется? Очевидно, что строить его прямым способом, сортируя суффиксы, дело долгое — O(N2logN), где N=|A|. Есть ряд алгоритмов, которые работают за O(NlogN), есть те, которые работают за O(N). Те которые O(N) весьма запутаны (например сначала построение суффиксного дерева, а потом из него уже собрать суффиксный массив). Если максимум эффективности в конкретной задаче не столь важен, то стоит подумать о понятности кода и остановиться на NlogN варианте. Далее пойдет по одному ходовому алгоритму из этих категорий.
Вспомним, как работает поразрядная сортировка: сначала распределяем элементы в корзины (buckets) подсчетом исходя из младшего разряда, потом проделываем то же самое со следующим разрядом и т.д. Здесь будем действовать схожим образом, но все-таки чуток по другому — если напрямую применять поразрядную сортировку к суффиксам, то получится O(N2).
Пусть на каком-то шаге мы отсортировали (точнее расположили по корзинам — buckets) строки согласно H первым символам. Мы можем пронумеровать эти части строк номерами их корзин. Но каждый суффикс S[i]=A[i..] встречается не только как элемент массива, но и как части других элементов массива, в частности в виде подстроки в позиции H суффикса S[i-H] (опустим для ясности краевые эффекты на конце строки — их можно обойти записыванием в конец нужного количества сентинелов). То есть пронумеровав первые H символов суффиксов номерами корзин, мы автоматически пронумеруем и вторые H символов. Тогда мы получим набор пар, состоящих из номеров корзин (какого-то шага). Отсортировав поразрядной сортировкой эти пары мы за O(N) получим строки, распиханные по корзинам по 2H первым символам. Таким образом количество обработанных символов на каждом шаге будет расти вдвое. Это дает O(logN) шагов и общую сложность алгоритма O(NlogN).
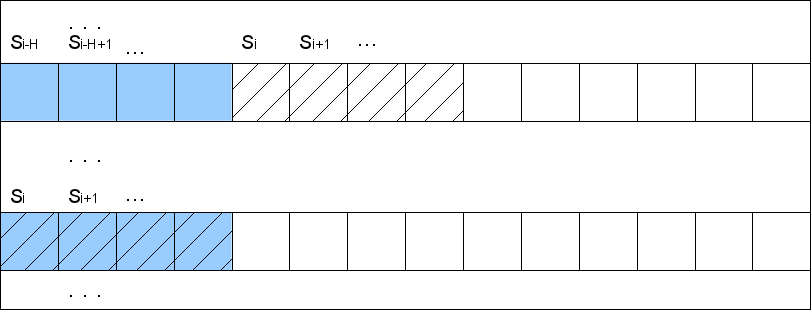
Еще небольшое замечание относительно первого шага. Если в последующих шагах нам приходится сортировать номера корзин, что у поразрядной сортировки не вызывает проблем, то первым шагом нам надо отсортировать строки по первому символу. В зависимости от природы алфавита может оказаться, что применить поразрядную сортировку там нельзя. Тогда можно применить любую другую сортировку, основанную на сравнениях со сложностью O(NlogN), и найти диапазоны корзин за O(N). Общую сложность алгоритма это не изменит.
Это достаточно новый алгоритм, опубликованный в 2003 году Каркайненом и Сандерсом. Сразу предупрежу, что данный алгоритм работает только на алфавитах, символы которых можно пронумеровать за O(N) времени (пронумеровать равносильно отсортировать, то есть нужно уметь сортировать за O(N) поразрядной сортировкой). Иное встречается редко, но все же бывает.
Алгоритм рекурсивный, то есть на каком-то этапе мы получаем такую-же задачу нахождения суффиксного массива для строки меньшей длины. Рассмотрим пример «mississippi». Итак, первое, что мы сделаем, это пронумеруем наши символы числами от 1 до N, перейдя к числовому алфавиту. Как мы упоминали, сделать это можно за O(N) поразрядной сортировкой. После этого исходные «настоящие» символы нас не интересуют, мы работаем только с числовым представлением строки. Можно забыть о том, что это когда-то было не числовой последовательностью.
Далее мы хотим построить супералфавит, который будет содержать все имеющиеся в тексте триграммы, и снова пронумеровать символы этого нового алфавита в лексикографическом порядке. Понятно, что этих триграмм не более чем символов в строке (меньше, если есть совпадающие). Так как мы хотим иметь возможность эффективно работать с этим алфавитом, то вариант каждый раз искать триграмму в супералфавите и возвращать ее лексикографическую позицию (лексикографическая позиция еще иногда называется рангом) не катит. Мы должны сразу так пронумеровать супералфавит, чтобы вопросов что это за триграмма не возникало вовсе. Для этого надо сопоставить каждому символу входной строки (она у нас числовая, не забыли?) номер триграммы в этой позиции. Делается это поразрядной сортировкой всех триграмм (вместе с дубликатами) из исходной строки с сохранением того, из какой позиции пришла триграмма. Последующая нумерация в таком случае не составляет труда.
Например, из A=«mississippi» можно получить триграммы {mis, iss, ssi,… ppi, pi$, i$$}, а в лексикографическом порядке {i$$, ipp, iss,… ssi}. Мы дополнили строку по мере надобности сентинелами и считаем их минимальными символами.
На этом этапе может оказаться, что все триграммы в строке разные. Это можно использовать как раннее терминальное условие, так как если триграммы разные, то их лексикографический порядок задает лексикографический порядок суффиксов (можно и не пользоваться этим условием, а просто продолжать сводить строку к более коротким, пока ответ не станет очевиден). Исходную строку мы можем представить в виде триграмм тремя способами: разбив на триграммы саму строку, строку без первого символа и строку без двух первых символов. Назовем эти представления строк T0, T1 и T2. Каждая из них где-то в три раза короче исходной. Если отсчитывать позиции от нуля, то эти представления можно будет назвать соответствующими группе суффиксов в позициях i mod 3 = 0, i mod 3 = 1 и i mod 3 = 2.
Далее делается финт ушами, смысл которого будет понятен позже: мы берем две из этих трех строк, для конкретности T1 и T2, представленных в виде триграмм, конкатенируем и передаем этому же алгоритму в рекурсивный вызов. Очевидно, длина переданной строки на треть короче исходной. На выходе из алгоритма мы ожидаем суффиксный массив (или, что эквивалентно, массив рангов). Перейдя обратно от триграмм к числовой строке, мы получим информацию о лексикографическом порядке между суффиксами групп 1 и 2.
Суффикс группы 0 можно представить как пару, состоящую из символа и суффикса группы 1, либо как тройку из двух символов и суффикса группы 2: A[3k..]=(A[3k],A[3k+1..])=(A[3k],A[3k+1],A[3k+2..]). Аналогичные выражения можно написать и для перевода других групп суффиксов в соседние. Представим суффиксы типа 0 как пары из символа и суффикса типа 1 (точнее ранга суффикса типа 1, сам суффикс нам неинтересен), после чего отсортируем их поразрядной сортировкой.
На этом этапе у нас есть результат рекурсивного вызова функции в виде взаимно отсортированных суффиксов типа 1 и 2, и отсортированные суффиксы типа 0. Нам надо слить их с помощью обычного слияния сортированных массивов, но при этом нам надо уметь эффективно сравнивать суффиксы типа 0 с типами 1 и 2. Для того, чтобы сравнить суффикс типа 0 с типом 1, надо перевести суффикс типа 0 в тип 1, а типа 1 в тип 2: (A[3l],A[3l+1..]) VS (A[3m+1],A[3m+2]..). Сравнить эти две пары просто: либо первый символ определяет порядок, либо если он равен, то порядок определяют порядок суффиксов группы 1 и 2, который нам известен из результатов рекурсивного вызова этого алгоритма. Для сравнения суффикса типов 0 и 2 цепочка чуток больше, но суть та же: (A[3l],A[3l+1],A[3l+2..]) VS (A[3m+2],A[3(m+1)],A[3(m+1)+1..]).
На первый взгляд непонятно, почему это все должно дать нам линейную сложность. Во-первых, разберемся со всем кроме рекурсивного вызова. Поразрядная сортировка супералфавита, маркировка суффиксов — это все O(N), поразрядная сортировка суффиксов группы 0 и слияние сортированных массивов — тоже O(N). Теперь рекурсивный вызов — мы вызываем алгоритм на 2/3 от исходной длины строки, таким образом сложность алгоритма T(N)=T(2N/3)+O(N). Если расписать это выражение подставляя его самого в себя, то получим сумму геометрической прогрессии с коэффициентом 2/3, а значит ограниченную O(N). Итоговая сложность таким образом O(N).
Вот и описано как применять суффиксный массив и как его строить. Алгоритмы достаточно объемные, но что поделать — задача весьма высокоуровневая. Описал я это все в достаточно общих чертах и не предоставил никакого кода по понятной причине — тогда и слов, и кода было бы слишком много. Как видим, алгоритмы быстрые и чуть более медленные существенно отличаются по сложности реализации, так что есть повод несколько раз подумать действительно ли вам нужно это делать, например, за O(N), а не за O(NlogN).
Еще я предвижу вопросы вида «где можно посмотреть готовую реализацию», «где почитать подробнее» и т.д. Готовых реализаций в стиле «просто допиши свой компаратор» лично я не видел, хотя страничка в википедии утверждает, что таковые существуют. Здесь и здесь есть объяснения и кое-какая реализация. Кроме того в оригинальной статье Каркайнена и Сандерса тоже есть код построения массива. Про NlogN построение можно почитать в статье Манбера и Майерса: Udi Manber, Gene Myers — «Suffix arrays: a new method for on-line string searches».
Материал статьи предполагает знание понятий суффикса и префикса строки, а также знание того, как работает бинарный поиск. Надо также представлять, что такое стабильная сортировка и поразрядная сортировка, а также понимание, что имеется ввиду под стабильной сортировкой подсчетом. Для некоторых частей нам понадобится знание задачи о минимуме на отрезке — Range Minimum Query (RMQ). Ну, в общем, вас предупредили: никто не говорил, что будет просто.
Применения суффиксного массива
Не все деревья одинаково полезны
Итак, чем же не устраивает нас дерево? Во-первых, это конечно то, что из за необходимости хранить ссылки на детей, родителя и т.п. размер используемой памяти в этом случае заметно больше, чем если эти ссылки не хранить. Во-вторых, если аллоцировать память под данные каким-нибудь стандартным аллокатором, то их «раскидает по разным углам», в результате обход дерева будет предполагать большое количество переходов в памяти, что плохо сказывается на на работе кэша памяти. Конечно есть уловки, которые позволяют эту проблему подавить: надо размещать узлы дерева в массиве, а вместо указателей использовать индекс в массиве. Тогда дерево будет представляться цельным куском памяти.
Ну это общие проблемы для всех деревьев. А что там с пресловутой алфавитной зависимостью? Посмотрим на практическую реализацию суффиксного дерева (если вы не сталкивались с ним, то для понимания сути проблемы это не важно). В каждом узле такого дерева могут быть ссылки на детей в количестве от 1 (например для терминальной вершины без ветвления) и до размера алфавита. Вот и возникает вопрос как хранить эти ссылки. Можно, например, в каждом узле держать массив ссылок размером с алфавит. Работать это будет быстро — узнать, есть ли соответствующий ребенок в данном узле можно за O(1). Но в большинстве ячеек массива будут храниться нулевые ссылки, а память на эти ячейки уйдет. Для небольших алфавитов (например, нуклеотиды в ДНК) черт с ним, но представьте себе китайские иероглифы? В принципе далеко ходить не надо: даже не case-sensitive русский алфавит заставляет призадуматься, а хотим ли мы столько пустых данных иметь.
Можно экономней расходовать память, помещая в некий динамически-изменяемый массив (вектор) только непустые ссылки, но тогда уже проверка наличия соответствующего ребенка узла за O(1) становится весьма сомнительной. Если хранить ссылки в отсортированном виде, то O(log(размер алфавита)). Можно попробовать поиграть с хэш-таблицами, но это будет иметь смысл только для сверхбольших алфавитов, и к тому же вводится еще один уровень косвенности. Да и строить такие деревья уже не O(n). В общем, в любом случае надо будет идти на какой-то компромисс между памятью и производительностью.
Суффиксный массив
В 1989 году Манбер и Майерс опубликовали статью, в которой описали такую структуру данных, как суффиксный массив, и как ее применять для поиска подстрок. Суффиксный массив — это массив лексикографически отсортированных суффиксов строк (если терминология незнакома, то можно глянуть раздел «постановка задачи» в этой статье). Вообще говоря, хранить сами суффиксы смысла нет, достаточно хранить позицию начала данного суффикса, но определение массива так легче воспринимается. Вот пример для строки «mississippi»:
| # | суффикс | номер суффикса |
|---|---|---|
| 1 | i | 11 |
| 2 | ippi | 8 |
| 3 | issippi | 5 |
| 4 | ississippi | 2 |
| 5 | mississippi | 1 |
| 6 | pi | 10 |
| 7 | ppi | 9 |
| 8 | sippi | 7 |
| 9 | sissippi | 4 |
| 10 | ssippi | 6 |
| 11 | ssissippi | 3 |
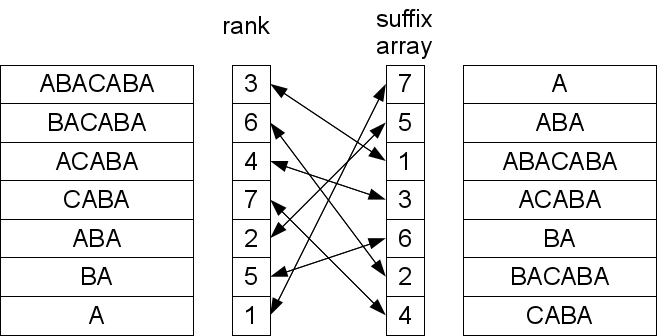
Также важное понятие ранг суффикса — то место, которое займет суффикс при сортировке, то есть его позиция в суффиксном массиве. Это взаимнообратные величины. Мы не будем их особо как-то различать, так как имея один массив, получить другой можно за O(N), так что можно всегда иметь под рукой оба.

Простейший поиск подстроки
Рассмотрим пример. Исходная строка «mississippi». Допустим, приходит к нам образец «sip». Простейший способ узнать, встречается ли образец в тексте, используя суффиксный массив, это взять первый символ образца и бинарным поиском (массив у нас отсортирован) найти диапазон с суффиксами, начинающимися на такую же букву. Так как все элементы в диапазоне отсортированы, а первые символы одинаковые, то оставшиеся после отбрасывания первого символа суффиксы тоже отсортированы. А значит, можно повторять процедуру сужения диапазона поиска до получения либо пустого диапазона, либо успешного нахождения всех символов образца. Очевидно, что таким образом за O(|X|log|A|) операций мы получим ответ.
| образец | sip | sip | sip |
|---|---|---|---|
| i | i | i | |
| ippi | ippi | ippi | |
| issippi | issippi | issippi | |
| ississippi | ississippi | ississippi | |
| mississippi | mississippi | mississippi | |
| pi | pi | pi | |
| ppi | ppi | ppi | |
| sippi | sippi | sippi | |
| sissippi | sissippi | sissippi | |
| ssippi | ssippi | ssippi | |
| ssissippi | ssissippi | ssissippi |
Точно такую же сложность получим, если будем применять бинарный поиск «в лоб»: с полными лексикографическими сравнениями строк по краям и в медиане с образцом: O(log|A|) сравнений со средней «ценой» сравнения O(|X|).
Быстрее
Неплохо, но можно лучше. На самом деле не обязательно сравнивать всю искомую строку с элементом массива. На каждой итерации бинарного поиска мы уточняем некий диапазон, внутри которого может находиться искомый элемент. Все строки в таком диапазоне в некотором смысле похожи. А именно, у данных строк может быть общий префикс с искомой строкой, так как у тех, что остались вне диапазона, общего префикса уж точно не будет (в том смысле, что мы не рассматриваем уже обработанную часть образца как часть префикса).
Допустим, мы знаем длину общего префикса оставшегося образца с краями текущего диапазона l=lcp(X,S[L]) и r=lcp(X,S[R]) для левого и правого края (lcp — longest common prefix). Первое утверждение заключается в том, что для любой строки внутри диапазона lcp не меньше, чем минимум этих двух чисел. Если бы это было не так, то значит при неизменной начальной части префикса была бы позиция, где символ сначала совпадал бы с соответствующим символом образца, потом не совпадал, а потом снова совпадал. Это противоречило бы отсортированности диапазона. Важно хорошо проникнуться этой идеей, так как дальше мы ее будем использовать как нечто само собой разумеющееся. Второе утверждение очевидно: если общий префикс образца и любой строки внутри диапазона не меньше m=min(l,r), то m символов можно пропускать сразу, зная, что они совпадают в любом случае, и сравнивать только начиная с m+1 (и получая в результате lcp для данной строки).

Таким образом мы применим оптимизированное сравнение строк в бинарном поиске строки «в лоб». В худшем случае, конечно, ничего мы от этого не выиграем: если искомый элемент находится на краю массива, но соседи совсем не похожи по lcp, то r (или l) будет мало каждый раз, m будет тоже мало, а значит придется проверять каждый символ по log|A| раз. Но экспериментальные наблюдения свидетельствуют, что для естественных текстов время поиска существенно сокращается по сравнению с O(log|A||X|), хотя про какую-то конкретную асимптотику утверждать что либо сложно.
В принципе, для практических применений этого уже вполне достаточно, но если хочется выжать все, то…
Еще быстрее
Это не предел. Позиции краев участка массива задают центр этого участка, и все такие конфигурации, которые реализуются при бинарном поиске являются подмножеством фиксированного набора размера |A|-2. Допустим мы заранее позаботились посчитать в этих конфигурациях величины ml=lcp(S[M],S[L]) и mr=lcp(S[M],S[R]), где M — середина участка между L и R, в которую мы пойдем на шаге бинарного поиска.

Посмотрим на один из краев, скажем, левый. Если посчитанный нами l<ml, то значит левый край похож на середину (и на любой элемент между ними) гораздо сильнее, чем нам хотелось бы, и значит результат сравнения заранее известен для всего участка между L и M: lcp(X,S[M])=l. Из этого непосредственно ясно, что искомый элемент точно не на этом участке, и если и искать его, то в противоположной половине. Если же l>ml, то значит середина похожа на левый край меньше, чем искомый образец. Значит lcp(X,S[M])=ml, а искомый элемент следует искать где-то между ними.
Естественно, ничего не меняется в рассуждениях, если заменить левый край на правый. Не рассмотренным оказался только один случай: l=ml и r=mr (если хоть одно равенство не верно, то результат известен согласно предыдущему абзацу). Тогда ясно, что lcp(X,S[M]) не меньше max(l,r), но для его точного определения и выяснения в какую сторону идти надо будет сравнивать символы (наконец то!) начиная с позиции max(l,r)+1.

Что же у нас получилось? Часть шагов бинарного поиска мы сделаем сравнивая несколько lcp между собой, а если уж и дойдет до сравнения символов, то не более одного раза на символ X (мы берем max(l,r)+1, а значит никогда не возвращаемся назад). Таким образом получаем сложность алгоритма O(log|A| + |X|) в худшем случае. Правда, нужны предпосчитаные lcp для суффиксов текста A, встречающихся в дереве поиска, индуцированного алгоритмом бинарного поиска.
Важно отметить, что если мы не будем знать mr, а только ml, то тоже ничего страшного. Мы лишаемся возможности заранее сказать, что вхождение отсутствует, но сложность это не ухудшает: просто не будем смотреть на правый край, только левый. Если l<ml, то ищем дальше в другой половине, а l сохраняется, если l>ml, то r берем как ml и ищем в этой половине, ну а если l=ml, то сравниваем медианный элемент с искомой строкой начиная с l+1-ой позиции. Назад мы не возвращаемся и в этом случае тоже, а значит можно обойтись lcp только для левых краев без ухудшения сложности алгоритма.
Предобработка LCP
Как вы помните, для эффективного поиска подстрок нам нужны были предпосчитаные lcp для определенных комбинаций суффиксов. Надо объяснить как их получать. Способы обычно сводятся к задаче о поиске минимума на отрезке — RMQ, поэтому алгоритмическая сложность алгоритма по большей части обусловлена тем, насколько эффективно вы умеете решать задачу RMQ. Более-менее простой алгоритм обойдется в O(NlogN) на предобработке и O(1) на запрос. То есть если вы используете построение суффиксного массива за O(NlogN), то вполне можно использовать его. Разумеется, если вы хотите строить суффиксный массив за линейное время, то придется применять алгоритм предобработки RMQ за линейное время с константными запросами.
Сначала построим так называемый lcp-массив — это массив значений lcp между лексикографически-соседними суффиксами (после того, как у нас построен суффиксный массив, какие суффиксы у нас соседние вопросов не вызывает). Если у нас есть lcp-массив, то нахождение lcp между двумя элементами сводится к поиску минимального значения на заданном отрезке lcp-массива, то есть задача RMQ — поиск минимума на отрезке — в чистом виде. Почему это так, понятно из соображений упорядоченности суффиксов: если бы lcp между двумя строками был больше, то все строки между ними тоже бы содержали как минимум такое же количество одинаковых символов в начале, и все lcp между этими строками были бы не меньше взаимного lcp крайних элементов.
Построить массив lcp достаточно просто. Конечно, идти по суффиксному массиву и считать lcp соседних элементов не получится — это O(N2). Но если идти по массиву в правильном порядке, то можно использовать информацию с предыдущего шага для расчетов. А именно, если перебирать суффиксы в том порядке, в котором они встречаются в исходной строке, то на каждом шаге lcp по сравнению с предыдущем шагом не может уменьшиться больше чем на 1, то есть может быть больше, может не измениться, но если уж станет меньше, то только на 1. Это происходит по следующей причине. Если вы выяснили, что lcp(A[i..],A[j..])=l, то отбрасывание первого символа, очевидно, уменьшает его на единицу: lcp(A[i+1..],A[j+1..])=l-1. Конечно, если i-ый и j-ый суффиксы оказались лексикографически соседними, то это не гарантирует, что i+1-ый и j+1-ый будут соседними — между ними, скорее всего, вклинятся другие. Но, как мы уже выяснили, lcp между ними — это минимальное lcp на всем отрезке между ними, а значит lcp между i+1-м суффиксом и лексикографически следующим за ним не меньше l-1.
| # | суффикс | шаг | lcp |
|---|---|---|---|
| 1 | i | 10 | 1 |
| 2 | ippi | 7 | 1 |
| 3 | issippi | 4 | 4 |
| 4 | ississippi | 2 | 0 |
| 5 | mississippi | 1 | 0 |
| 6 | pi | 9 | 1 |
| 7 | ppi | 8 | 0 |
| 8 | sippi | 6 | 2 |
| 9 | sissippi | 3 | 1 |
| 10 | ssippi | 5 | 3 |
| 11 | ssissippi | skip |
Это позволяет пропустить все символы до предпоследнего (l-1), так как мы уверены, что они равны, и сравнивать только l-ый символ и далее. Значит, любые сделанные нами проверки либо увеличивают текущее lcp, либо заставляют нас переходить к следующей итерации. Таким образом пройдя все суффиксы кроме лексикографически последнего (его надо пропустить) мы получим lcp-массив за линейное время O(N).
Ну вот и все. Осталось найти RMQ для необходимых нам пар суффиксов. Решение RMQ состоит из предобработки и, собственно, ответов на запросы минимума между элементами. Так как основная вычислительная нагрузка приходится на предобработку, а выполнение запросов можно сделать O(1), то вообще говоря необязательно выписывать в явном виде интересующие нас пары и lcp между ними, так как за O(1) мы можем ответить об lcp произвольной пары суффиксов, в том числе и тех, которые играют роль в бинарном поиске. Учитывая, что это нас избавляет от необходимости думать как адресоваться к сохраненным значениям, это очень здорово. Если все-таки хочется хранить lcp в уже посчитанном виде, то надо правильно пронумеровать состояния в дереве поиска — почитайте про расположение в памяти и адресацию в бинарной куче.
Про то, как решать RMQ я писать не буду — на Хабре уже была хорошая статья про простой вариант за O(NlogN), и, надеюсь, будет продолжение, в котором напишут про хардкорный вариант за O(N) — алгоритм Фараха-Колтона и Бендера.
Построение суффиксного массива
Замечательно, вот мы знаем как применить суффиксный массив, но откуда он у нас возьмется? Очевидно, что строить его прямым способом, сортируя суффиксы, дело долгое — O(N2logN), где N=|A|. Есть ряд алгоритмов, которые работают за O(NlogN), есть те, которые работают за O(N). Те которые O(N) весьма запутаны (например сначала построение суффиксного дерева, а потом из него уже собрать суффиксный массив). Если максимум эффективности в конкретной задаче не столь важен, то стоит подумать о понятности кода и остановиться на NlogN варианте. Далее пойдет по одному ходовому алгоритму из этих категорий.
За O(NlogN)
Вспомним, как работает поразрядная сортировка: сначала распределяем элементы в корзины (buckets) подсчетом исходя из младшего разряда, потом проделываем то же самое со следующим разрядом и т.д. Здесь будем действовать схожим образом, но все-таки чуток по другому — если напрямую применять поразрядную сортировку к суффиксам, то получится O(N2).
Пусть на каком-то шаге мы отсортировали (точнее расположили по корзинам — buckets) строки согласно H первым символам. Мы можем пронумеровать эти части строк номерами их корзин. Но каждый суффикс S[i]=A[i..] встречается не только как элемент массива, но и как части других элементов массива, в частности в виде подстроки в позиции H суффикса S[i-H] (опустим для ясности краевые эффекты на конце строки — их можно обойти записыванием в конец нужного количества сентинелов). То есть пронумеровав первые H символов суффиксов номерами корзин, мы автоматически пронумеруем и вторые H символов. Тогда мы получим набор пар, состоящих из номеров корзин (какого-то шага). Отсортировав поразрядной сортировкой эти пары мы за O(N) получим строки, распиханные по корзинам по 2H первым символам. Таким образом количество обработанных символов на каждом шаге будет расти вдвое. Это дает O(logN) шагов и общую сложность алгоритма O(NlogN).

Еще небольшое замечание относительно первого шага. Если в последующих шагах нам приходится сортировать номера корзин, что у поразрядной сортировки не вызывает проблем, то первым шагом нам надо отсортировать строки по первому символу. В зависимости от природы алфавита может оказаться, что применить поразрядную сортировку там нельзя. Тогда можно применить любую другую сортировку, основанную на сравнениях со сложностью O(NlogN), и найти диапазоны корзин за O(N). Общую сложность алгоритма это не изменит.
За O(N)
Это достаточно новый алгоритм, опубликованный в 2003 году Каркайненом и Сандерсом. Сразу предупрежу, что данный алгоритм работает только на алфавитах, символы которых можно пронумеровать за O(N) времени (пронумеровать равносильно отсортировать, то есть нужно уметь сортировать за O(N) поразрядной сортировкой). Иное встречается редко, но все же бывает.
Алгоритм рекурсивный, то есть на каком-то этапе мы получаем такую-же задачу нахождения суффиксного массива для строки меньшей длины. Рассмотрим пример «mississippi». Итак, первое, что мы сделаем, это пронумеруем наши символы числами от 1 до N, перейдя к числовому алфавиту. Как мы упоминали, сделать это можно за O(N) поразрядной сортировкой. После этого исходные «настоящие» символы нас не интересуют, мы работаем только с числовым представлением строки. Можно забыть о том, что это когда-то было не числовой последовательностью.
Далее мы хотим построить супералфавит, который будет содержать все имеющиеся в тексте триграммы, и снова пронумеровать символы этого нового алфавита в лексикографическом порядке. Понятно, что этих триграмм не более чем символов в строке (меньше, если есть совпадающие). Так как мы хотим иметь возможность эффективно работать с этим алфавитом, то вариант каждый раз искать триграмму в супералфавите и возвращать ее лексикографическую позицию (лексикографическая позиция еще иногда называется рангом) не катит. Мы должны сразу так пронумеровать супералфавит, чтобы вопросов что это за триграмма не возникало вовсе. Для этого надо сопоставить каждому символу входной строки (она у нас числовая, не забыли?) номер триграммы в этой позиции. Делается это поразрядной сортировкой всех триграмм (вместе с дубликатами) из исходной строки с сохранением того, из какой позиции пришла триграмма. Последующая нумерация в таком случае не составляет труда.
Например, из A=«mississippi» можно получить триграммы {mis, iss, ssi,… ppi, pi$, i$$}, а в лексикографическом порядке {i$$, ipp, iss,… ssi}. Мы дополнили строку по мере надобности сентинелами и считаем их минимальными символами.
| оригинальная строка: | m | i | s | s | i | s | s | i | p | p | i |
| числовая строка: | 2 | 1 | 4 | 4 | 1 | 4 | 4 | 1 | 3 | 3 | 1 |
| триграммы: | mis | iss | ssi | sis | iss | ssi | sip | ipp | ppi | pi$ | i$$ |
| нумерация триграмм: | 4 | 3 | 9 | 8 | 3 | 9 | 7 | 2 | 6 | 5 | 1 |
На этом этапе может оказаться, что все триграммы в строке разные. Это можно использовать как раннее терминальное условие, так как если триграммы разные, то их лексикографический порядок задает лексикографический порядок суффиксов (можно и не пользоваться этим условием, а просто продолжать сводить строку к более коротким, пока ответ не станет очевиден). Исходную строку мы можем представить в виде триграмм тремя способами: разбив на триграммы саму строку, строку без первого символа и строку без двух первых символов. Назовем эти представления строк T0, T1 и T2. Каждая из них где-то в три раза короче исходной. Если отсчитывать позиции от нуля, то эти представления можно будет назвать соответствующими группе суффиксов в позициях i mod 3 = 0, i mod 3 = 1 и i mod 3 = 2.
| T0: | mis | sis | sip | pi$ |
| 4 | 8 | 7 | 5 | |
| T1: | iss | iss | ipp | i$$ |
| 3 | 3 | 2 | 1 | |
| T2: | ssi | ssi | ppi | |
| 9 | 9 | 6 |
Далее делается финт ушами, смысл которого будет понятен позже: мы берем две из этих трех строк, для конкретности T1 и T2, представленных в виде триграмм, конкатенируем и передаем этому же алгоритму в рекурсивный вызов. Очевидно, длина переданной строки на треть короче исходной. На выходе из алгоритма мы ожидаем суффиксный массив (или, что эквивалентно, массив рангов). Перейдя обратно от триграмм к числовой строке, мы получим информацию о лексикографическом порядке между суффиксами групп 1 и 2.
Суффикс группы 0 можно представить как пару, состоящую из символа и суффикса группы 1, либо как тройку из двух символов и суффикса группы 2: A[3k..]=(A[3k],A[3k+1..])=(A[3k],A[3k+1],A[3k+2..]). Аналогичные выражения можно написать и для перевода других групп суффиксов в соседние. Представим суффиксы типа 0 как пары из символа и суффикса типа 1 (точнее ранга суффикса типа 1, сам суффикс нам неинтересен), после чего отсортируем их поразрядной сортировкой.
На этом этапе у нас есть результат рекурсивного вызова функции в виде взаимно отсортированных суффиксов типа 1 и 2, и отсортированные суффиксы типа 0. Нам надо слить их с помощью обычного слияния сортированных массивов, но при этом нам надо уметь эффективно сравнивать суффиксы типа 0 с типами 1 и 2. Для того, чтобы сравнить суффикс типа 0 с типом 1, надо перевести суффикс типа 0 в тип 1, а типа 1 в тип 2: (A[3l],A[3l+1..]) VS (A[3m+1],A[3m+2]..). Сравнить эти две пары просто: либо первый символ определяет порядок, либо если он равен, то порядок определяют порядок суффиксов группы 1 и 2, который нам известен из результатов рекурсивного вызова этого алгоритма. Для сравнения суффикса типов 0 и 2 цепочка чуток больше, но суть та же: (A[3l],A[3l+1],A[3l+2..]) VS (A[3m+2],A[3(m+1)],A[3(m+1)+1..]).
На первый взгляд непонятно, почему это все должно дать нам линейную сложность. Во-первых, разберемся со всем кроме рекурсивного вызова. Поразрядная сортировка супералфавита, маркировка суффиксов — это все O(N), поразрядная сортировка суффиксов группы 0 и слияние сортированных массивов — тоже O(N). Теперь рекурсивный вызов — мы вызываем алгоритм на 2/3 от исходной длины строки, таким образом сложность алгоритма T(N)=T(2N/3)+O(N). Если расписать это выражение подставляя его самого в себя, то получим сумму геометрической прогрессии с коэффициентом 2/3, а значит ограниченную O(N). Итоговая сложность таким образом O(N).
Заключение
Вот и описано как применять суффиксный массив и как его строить. Алгоритмы достаточно объемные, но что поделать — задача весьма высокоуровневая. Описал я это все в достаточно общих чертах и не предоставил никакого кода по понятной причине — тогда и слов, и кода было бы слишком много. Как видим, алгоритмы быстрые и чуть более медленные существенно отличаются по сложности реализации, так что есть повод несколько раз подумать действительно ли вам нужно это делать, например, за O(N), а не за O(NlogN).
Еще я предвижу вопросы вида «где можно посмотреть готовую реализацию», «где почитать подробнее» и т.д. Готовых реализаций в стиле «просто допиши свой компаратор» лично я не видел, хотя страничка в википедии утверждает, что таковые существуют. Здесь и здесь есть объяснения и кое-какая реализация. Кроме того в оригинальной статье Каркайнена и Сандерса тоже есть код построения массива. Про NlogN построение можно почитать в статье Манбера и Майерса: Udi Manber, Gene Myers — «Suffix arrays: a new method for on-line string searches».
