
Нейронные сети глубокого обучения достигли больших успехов в распознавании образов. В тоже время текстовые капчи до сих пор используются в некоторых известных сервисах бесплатной электронной почты. Интересно смогут ли нейронные сети глубоко обучения справится с задачей распознавания текстовой капчи? Если да то как?
Что такое текстовая капча?
Капча (англ. “CAPTCHA”) — это тест на “человечность”. То есть задача, которую легко решает человек, в то время как для машины эта задача должна быть сложной. Зачастую используется текст со слипшимися буквами, пример на картинке ниже, также картинку дополнительно подвергают оптическим искажениям.
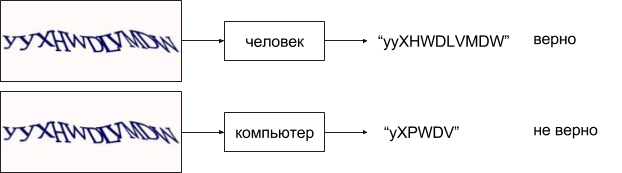
Капча, как правило, используется на странице регистрации для защиты от ботов рассылающих спам.
Полносверточная нейронная сеть
Если буквы “слиплись”, то их обычно очень трудно разделить эвристическими алгоритмами. Следовательно, нужно искать каждую букву в каждом месте картинки. С этой задачей справится полносверточная нейронная сеть. Полносверточная сеть — сверточная сеть без полносвязного слоя. На вход такой сети подается изображение, на выходе она выдает тоже изображение или несколько изображений (карты центров).
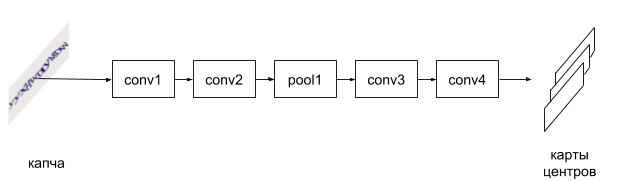
Количество карт центров равно длине алфавита символов использованных в определенной капче. На картах центров отмечаются центры букв. Масштабное преобразование, которое в сети происходит из-за наличия пуллинг слоев, учитывается. Ниже показан пример карты символа для символа “D”
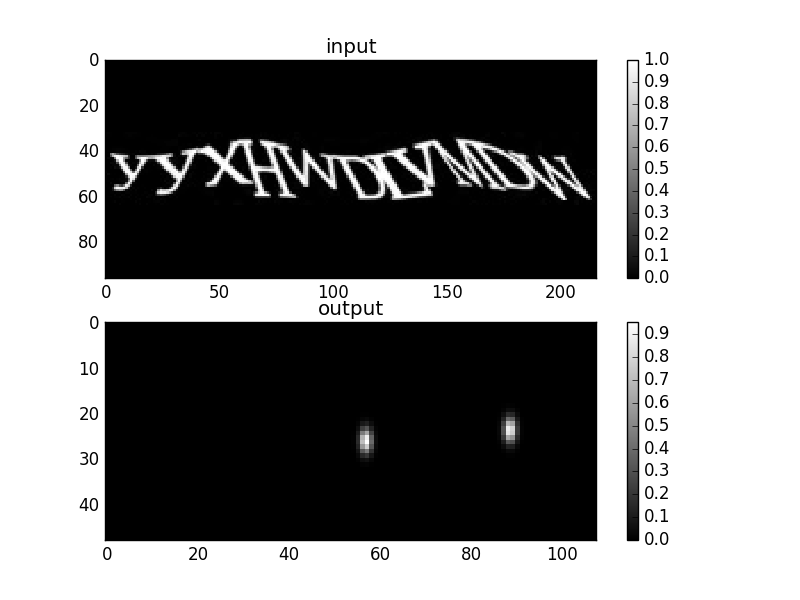
В данном случае используются сверточные слои с паддингом так, чтобы размер изображений на выходе сверточного слоя равнялся размеру изображений на входном слое. Профиль пятна на карте символа задается двумерной гауссовой функцией с ширинами 1.3 и 2.6 пикселей.
Первоначально полносверточная сеть была проверена на символе “R”:

Для проверки применялась небольшая сеть с 2мя пуллингами, натреннированная на CPU. Убедившись, что идея хоть как то работает, я приобрел б/у видеокарту Nvidia GTX 760, 2GB. Это дало мне возможность тренировать более крупные сети для всех символов алфавита, а также ускорило обучение (примерно в 10 раз). Для тренировки сети использовалась библиотека Theano, на текущий момент уже не поддерживаемая.
Тренировка на генераторе
Разметить большой датасет вручную казалось делом долгим и трудозатратным, поэтому было решено генерировать капчи специальным скриптом. При этом карты центров генерируются автоматически. Мною был подобран шрифт, используемый в капче для сервиса Hotmail, сгенерированная капча визуально была похожа по стилю на реальные капчи:

Финальная точность тренировки на сгенерированных капчах, как оказалось, в 2 раза ниже, по сравнению с тренировкой на реальных капчах. Вероятно, такие нюансы как степень пересечения символов, масштаб, толщина линий символов, параметры искажения и т. п., важны, и в генераторе эти нюансы воспроизвести не удалось. Сеть тренированная на сгенерированных капчах давала точность на реальных капчах около 10%, точность — какой процент капч распознался правильно. Капча считается распознанной, если все символы в ней распознаны правильно. В любом случае этот эксперимент показал, что метод рабочий, и требуется повысить точность распознавания.
Тренировка на реальном датасете
Для ручной разметки датасета реальных капч был написан скрипт на Matlab с графическим интерфейсом:
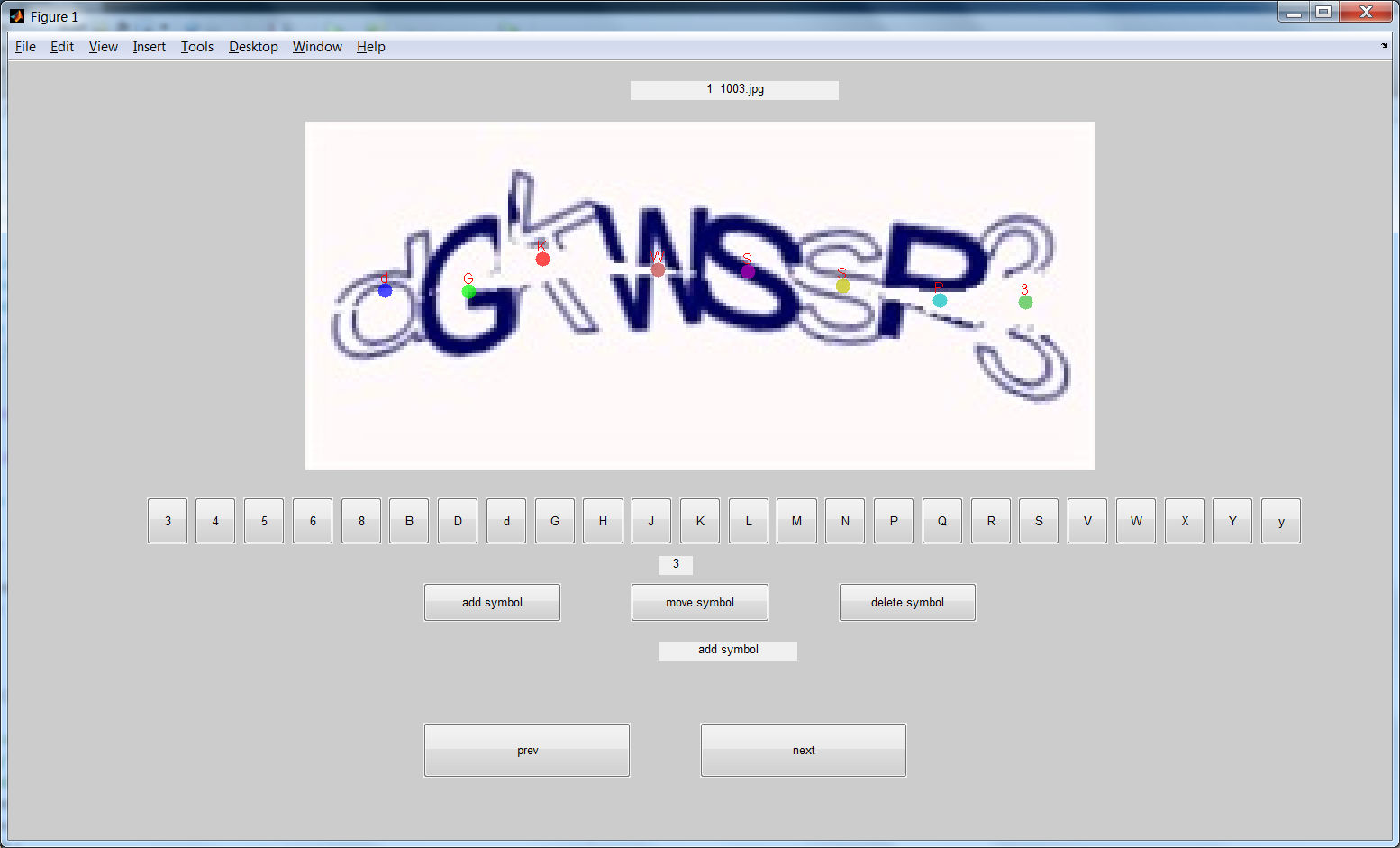
Здесь кружочки можно расставлять и двигать мышкой. Кружочком отмечается центр символа. Ручная разметка занимала 5-15 часов, однако есть сервисы, где за не большую плату размечают вручную датасеты. Однако, как оказалось, сервис Amazon Mechanical Turk не работает с российскими заказчиками. Разместил заказ на разметку датасета на известном сайте фриланса. К сожалению, качество разметки было не идеальным, поправлял разметку самостоятельно. Кроме того, поиск исполнителя занимает время (1 неделя) и также это показалось дорого: 30 долларов за 560 размеченных капч. От данного способа отказался, в итоге пришел к использованию сайтов ручного распознавания капч, где самая низкая стоимость 1 доллар за 2000 капч. Но полученный ответ там — это строка. Таким образом, ручной расстановки центров избежать не удалось. Более того, исполнители в таких сервисах допускают ошибки или вовсе действуют недобросовестно, печатая произвольную строку в ответе. В итоге приходилось проверять и исправлять ошибки.
Более глубокая сеть
Очевидно точность распознавания была недостаточна, поэтому возник вопрос подбора архитектуры. Меня интересовал вопрос “видит” ли один пиксель на выходном изображении весь символ на входном изображении:
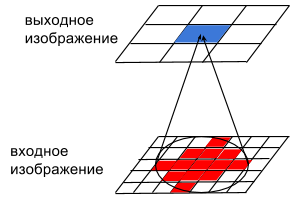
Таким образом, мы рассматриваем один пиксель на выходном изображении, и есть вопрос: значения каких пикселей на входном изображении влияют на значения этого пикселя? Я рассуждал так: если пиксель видит не весь символ, то используется не вся информация о символе и точность хуже. Для определения размера этой области видимости (будем называть ее так), я провел следующий эксперимент: установил все веса сверточных слоев равным 0.01, а смещения равным 0, на вход сети подается изображение, в котором значения всех пикселей равны 0 кроме центрального. В результате на выходе сети получается пятно:

Форма данного пятна близка к форме гауссовой функции. Форма получившегося пятна вызывает вопрос, почему пятно круглое, тогда как ядра сверток в сверточных слоях квадратные? (В сети использовались ядра сверток 3x3 и 5x5). Мое объяснение такое: это похоже на центральную предельную теорему. В ней, как и здесь, присутствует стремление к гауссовому распределению. Центральная предельная теорема утверждает, что для случайных величин, даже с разными распределениями, распределение их суммы равно свертке распределений. Таким образом, если мы сворачиваем любой сигнал сам с собой много раз, то по центральной предельной теореме результат стремится к гауссовой функции, а ширина гауссовской функции растет как корень из количества сверток (слоев). Если для такой же сети с константными весами посмотреть, где в выходном изображении значения пикселей больше нуля, то получается все таки квадратная область (см. рисунок ниже), размер этой области пропорционален сумме размеров сверток в сверточных слоях сети.

Раньше думал, что из-за ассоциативного свойства свертки две последовательные свертки 3x3 эквивалентны свертке 5x5 и потому, если свернуть 2 ядра 3x3 получится одно ядро 5x5. Однако, потом пришел к выводу, что это не эквивалентно хотя бы потому, что у двух сверток 3x3 9*2=18 параметров, а у одной 5x5 25 параметров, таким образом, у свертки 5x5 больше степеней свободы. В итоге, на выходе сети получается гауссова функция с шириной меньше суммы размеров сверток в слоях. Здесь ответил на вопрос какие пиксели на выходе подвержены влиянию одного пикселя на входе. Хотя изначально вопрос ставился обратный. Но оба вопросы эквивалентны, что можно понять из рисунка:

На рисунке можно представить, что это вид на изображения с боку или, что у нас высота изображений равна 1. Каждый из пикселей A и B имеет свою зону влияния на выходном изображении (обозначены синим цветом): для А это D-C, для B это C-E, на значения пикселя C влияют значения пикселей A и B и значения всех пикселей между A и B. Расстояния равны: AB = DC = CE (с учетом масштабирования: в сети присутствуют пуллинг слои, поэтому входное и выходное изображения имеют разные разрешения). В итоге, получается следующий алгоритм нахождения размера области видимости:
- задаем константные веса в сверточных слоях, весам-смещениям задаем значения 0
- на вход подаем изображения с одним ненулевым пикселем
- получаем размер пятна на выходе
- умножаем этот размер на коэффициент учитывающий разное разрешение входного и выходного слоя (например, если у нас 2 пулинга в сети, то разрешение на выходе в 4 раза меньше, чем на входе, значит этот размер надо умножать на 4).
Чтобы посмотреть какие признаки сеть использует, провел следующий эксперимент: в тренированную сеть подаем изображение капчи, на выходе получаем изображения с отмеченными центрами символов, из них выбираем какой-нибудь задетектированный символ, на изображениях-картах центров оставляем ненулевой только ту карту, которая соответствует рассматриваемому символу. Такой выход сети запоминаем как
 , затем градиентным спуском минимизируем функцию:
, затем градиентным спуском минимизируем функцию:
Здесь
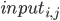 — входное изображение сети,
— входное изображение сети, 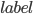 — выходные изображения сети,
— выходные изображения сети,  — некоторая константа, которая подбирается экспериментально (
— некоторая константа, которая подбирается экспериментально ( ). При такой минимизации вход и выход сети считаются переменными, а веса сети константами. Начальное значение переменной
). При такой минимизации вход и выход сети считаются переменными, а веса сети константами. Начальное значение переменной 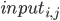 это изображение капчи, является начальной точкой оптимизации алгоритма градиентного спуска. При такой минимизации мы уменьшаем значения пикселей на входе изображения, при этом сдерживаем значения пикселей на выходном изображении, в результате оптимизации на входном изображении остаются только те пиксели, которые сеть использует в распознавании символа.
это изображение капчи, является начальной точкой оптимизации алгоритма градиентного спуска. При такой минимизации мы уменьшаем значения пикселей на входе изображения, при этом сдерживаем значения пикселей на выходном изображении, в результате оптимизации на входном изображении остаются только те пиксели, которые сеть использует в распознавании символа. Что получилось:
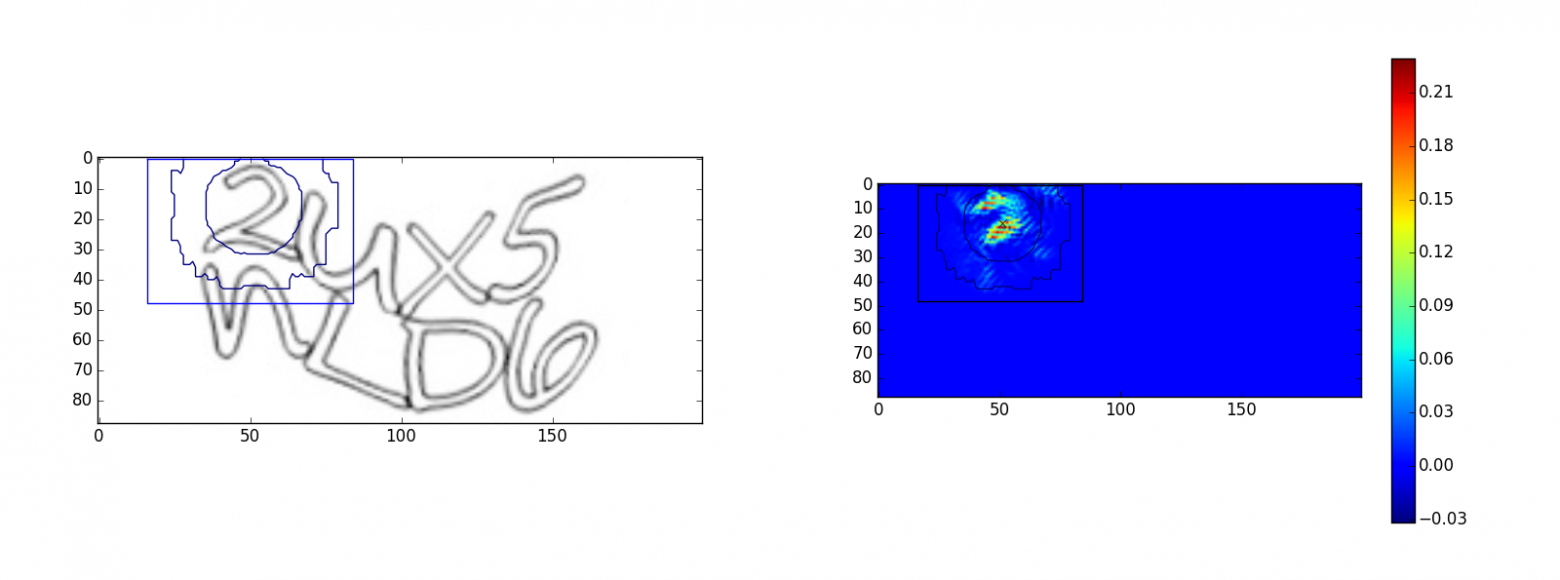
Для символа “2”:
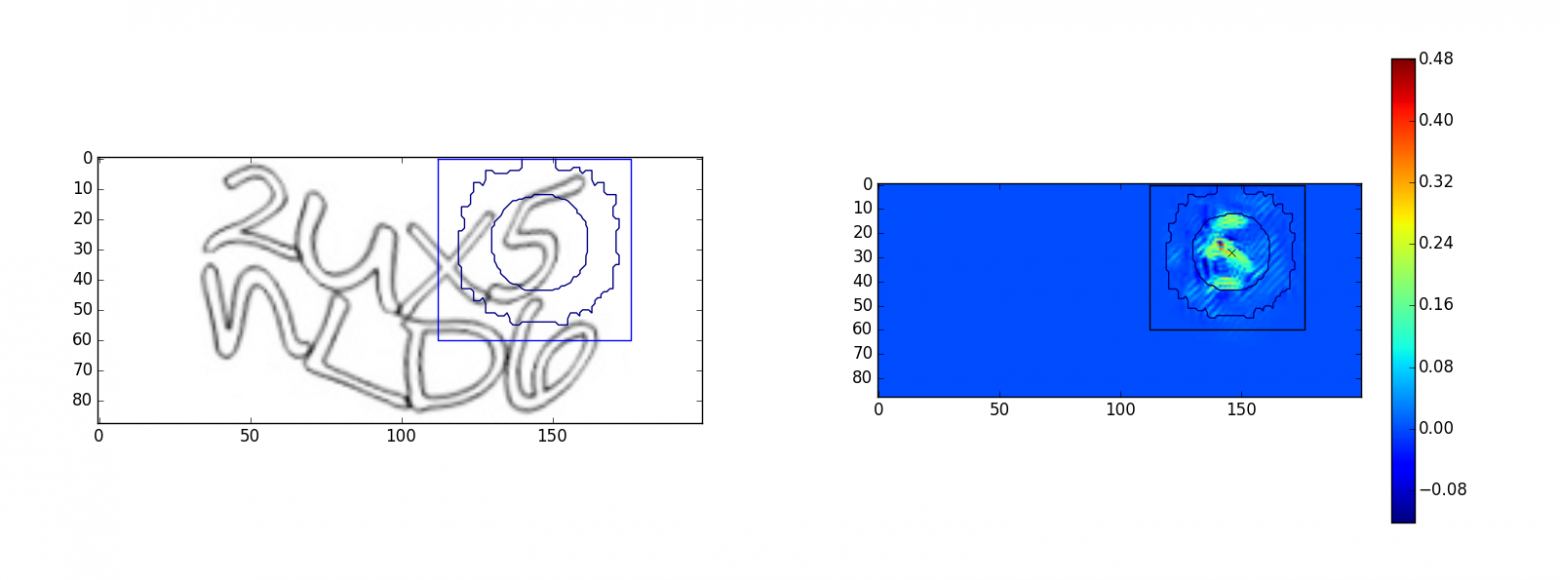
Для символа “5”:
Для символа “L”:

Для символа “u”:

Изображения слева — исходные изображения капч, изображения справа — это оптимизированное изображение
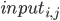 . Квадратом на изображениях обозначена область видимости output>0, окружности на рисунке — это линии уровня Гауссовой функции области видимости. Малая окружность — уровень 35% от максимального значения, большая окружность — уровень 3%. Примеры показывают, что сеть видит в пределах своей области видимости. Однако, у символа “u” наблюдается выход за область видимости, возможно это частичное ложное срабатывание на символ “n”.
. Квадратом на изображениях обозначена область видимости output>0, окружности на рисунке — это линии уровня Гауссовой функции области видимости. Малая окружность — уровень 35% от максимального значения, большая окружность — уровень 3%. Примеры показывают, что сеть видит в пределах своей области видимости. Однако, у символа “u” наблюдается выход за область видимости, возможно это частичное ложное срабатывание на символ “n”. Было проведено много экспериментов с архитектурой сети, чем более глубокая и широкая сеть, тем более сложные капчи она может распознавать, самой универсальной архитектурой оказалась следующая:

Синим цветом, поверх стрелок, показано количество изображений (feature maps). c- сверточный слой, p — max-pooling слой, зеленым цветом внизу показаны размеры ядер. В сверточных слоях используются ядра 3x3 и 5x5 без strade, пуллинг слой имеет патч 2x2. После каждого сверточного слоя есть ReLU слой (на рисунке не показан). На вход подается одно изображение, на выходе получется 24 (количество символов в алфавите). В сверточных слоях паддинг подобран таким образом, чтобы на выходе слоя размер изображения был таким же как и на входе. Паддинг добавляет нули, однако это никак не влияет на работу сети, потому что значение фонового пикселя капчи — 0, так как всегда берется негативное изображение (белые буквы по черному фону). Паддинг лишь незначительно замедляет работу сети. Так как в сети 2 пуллинг слоя, то разрешение изображения на выходе в 4 раза меньше разрешения изображения на входе, таким образом каждый пуллинг уменьшает разрешение в 2 раза, например, если на входе у нас капча размером 216x96 то на выходе будет 24 изображения размером 54x24.
Улучшения
Переход от решателя SGD к решателю ADAM дал заметное ускорение обучения, и финальное качество стало лучше. Решатель ADAM импортировал из модуля lasagne и использовал внутри theano-кода, параметр learning rate ставил 0.0005, регуляризация L2 была добавлена через градиент. Было замечено, что от тренировки к тренировке результат получается разный. Объясняю это так: алгоритм градиентного спуска застревает в недостаточно оптимальном локальном минимуме. Частично поборол это следующим образом: запускал тренировку несколько раз и выбирал несколько самых лучших результатов, затем продолжал их тренировать еще несколько эпох, после из них выбирал один лучший результат и уже этот единственный лучший результат долго тренировал. Таким образом удалось избежать застревания в недостаточно оптимальных локальных минимумах и финальное значение функции ошибок (loss) получалась достаточно малым. На рисунке показан график — эволюция значения функции ошибок:

По оси x — число эпох, по оси y — значение функции ошибок. Разными цветами показаны разные тренировки. Порядок обучения примерно такой:
1) запускаем 20 тренировок по 10 эпох
2) выбираем 10 лучших результатов (по наименьшему значению loss) и тренируем их еще 100 эпох
3) выбираем один лучший результат и продолжаем тренировать его еще 1500 эпох.
Это занимает около 12 часов. Конечно, для экономии памяти, данные тренировки проводились последовательно, например, в пункте 2) 10 тренировок проводились последовательно одна за другой, для этого провел модификацию решателя ADAM от Lasagne, чтобы иметь возможность сохранять и загружать состояние решателя в переменные.
Разбиение датасета на 3 части позволяло отслеживать переобучение сети:
1 часть: тренировочный датасет — исходный, на котором сеть обучается
2 часть: тестовый датасет, на котором сеть проверяется в процессе тренировки
3 часть: отложенный датасет, на нем проверяется качество обучения после тренировки
Датасеты 2 и 3 небольшие, в моем случае было по 160 капч в каждом, также по датасету 2 определяется оптимальный порог срабатывания, порог который устанавливается на выходное изображение. Если значение пикселя превышает порог, то в данном месте обнаружен соответствующий символ. Обычно оптимальное значение порога срабатывания находится в диапазоне 0.3 — 0.5. Если точность на тестовом датасете значительно ниже, чем точность на тренировочном датасете — это значит что произошло переобучение и тренировочный датасет необходимо увеличить. В случае, если эти точности примерно одинаковы, но не высокие, то архитектуру нейронной сети нужно усложнять, а тренировочный датасет увеличивать. Усложнять архитектуру сети можно двумя путями: увеличивать глубину или увеличивать ширину.
Предварительная обработка изображений также повышала точность распознавания. Пример предобработки:

В данном случае методом наименьших квадратов найдена средняя линия повернутой строки, производится поворот и масштабирование, масштабирование проводится по средней высоте строки. Сервис Hotmail часто делает разнообразные искажения:



Эти искажения необходимо компенсировать.
Неудачные идеи
Всегда интересно почитать про чужие неудачи, опишу их здесь.
Существовала проблема малого датасета: для качественного распознавания требовался большой датасет, который требовалось разметить вручную (1000 капч). Мной предпринимались различные попытки каким-то образом обучить сеть качественно на малом датасете. Делал попытку обучать сеть на результатах распознавания другой сети. при этом выбирал только те капчи и те места изображений, в которых сеть была уверена. Уверенность определял по значению пикселя на выходном изображении. Таким образом можно увеличить датасет. Однако идея не сработала, после нескольких итераций обучения качество распознавания сильно ухудшилось: сеть не распознавала некоторые символы, путала их, то есть ошибки распознавания накапливались.
Другая попытка обучиться на малом датасете — использовать сиамские сети, сиамская сеть на входе требует пару капч, если у нас датасет из N капч, то пар будет N2, получаем гораздо больше обучающих примеров. Cеть преобразует капчу в карту векторов. В качестве метрики сходства векторов выбрал скалярное произведение. Предполагалось что сиамская сеть будет работать следующим образом. Сеть сравнивает часть изображения на капче с некоторым эталонным изображением символа, если сеть видит, что символ тот же с учетом искажения, то считается, что в данном месте качи есть соответствующий символ. Сиамская сеть тренировалась с трудом, часто застревала в неоптимальном локальном минимуме, точность была заметно ниже точности обычной сети. Возможно проблема была в неправильном выборе метрики сходства векторов.
Также была идея использовать автоэнкодер для предварительного обучения нижней части сети (та, что ближе к входу), чтобы ускорить обучение. Автоэнкодер — это сеть, которая обучается выдавать на выходном изображении то же что и подается на вход, при этом в архитектуре автоэнкодера организуют узкий участок. Тренеровка автоэнкодера есть обучение без учителя.
Пример работы автоэкодера:
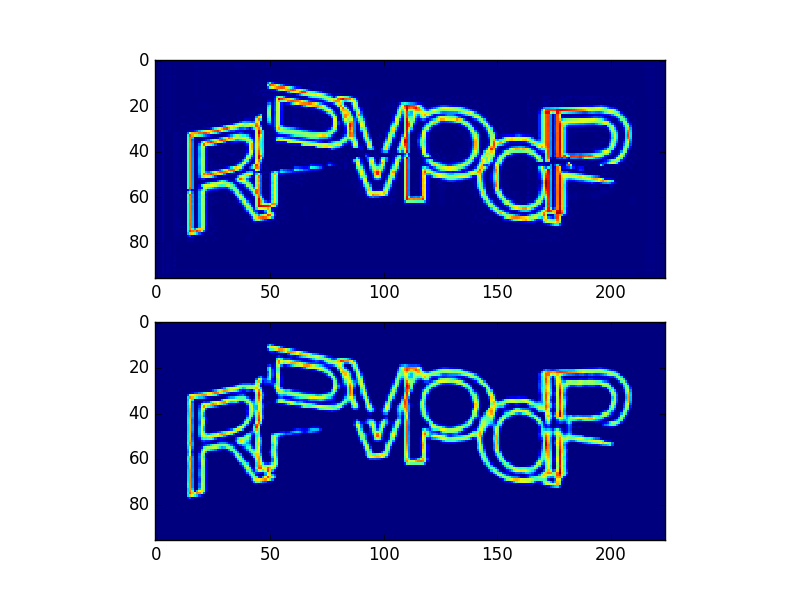
Первое изображение — входное, второе — выходное.
У обученного автоэнкодера берут нижнюю часть сети, добавляют новых необученных слоев, все это дотренировывают на требуемую задачу. В моем случае применение автоэнкодера никак не ускоряло обучение сети.
Также был пример капчи, которая использовала цвет:


На данной капче описанный метод с полносверточной нейронной сетью не давал результата, он не появился даже после различных предобработок изображения повышающих контрастность. Предполагаю что, полносверточные сети плохо справляются с неконтрастными изображениями. Тем не менее, данную капчу удалось распознать обычной сверточной сетью с полносвязным слоем, получена точность около 50%, определение координат символов осуществлялось специальным эвристическим алгоритмом.
Результат
| Примеры | Точность | Коментарий |
|---|---|---|
  |
42 % | Капча Микрософт , jpg |
 |
61 % | |
 |
63 % | |
 |
93 % | капча mail.ru, 500x200, jpg |
 |
87 % | капча mail.ru, 300x100, jpg |
 |
65 % | Капча Яндекс, русские слова, gif |
 |
70 % | капча Steam, png |
 |
82 % | капча World Of Tanks, цифры, png |
Что еще можно было бы улучшить
Можно было бы сделать автоматическую разметку центров символов. Сервисы ручного распознавания капч выдают лишь распознанные строки, поэтому автоматическая разметка центров помогла бы полностью автоматизировать разметку тренировочного датасета. Идея такова: выбрать только те капчи, в которых каждый символ встречается один раз, на каждый символ натренировать отдельную обычную сверточную сеть, такая сеть будет отвечать лишь на вопрос: есть ли в данной капче символ или нет? Затем посмотреть какие признаки использует сеть, используя метод минимизация значений пикселей входной картинки (описано выше). Полученные признаки позволят локализовать символ, далее тренируем полносверточную сеть на полученных центрах символов.
Выводы
Текстовые капчи распознаются полносверточной нейронной сетью в большинстве случаев. Вероятно, уже настало время отказываться от текстовых капч. Google давно не использует текстовую капчу, вместо текста предлагаются картинки с различными предметами, которые нужно распознать человеку:
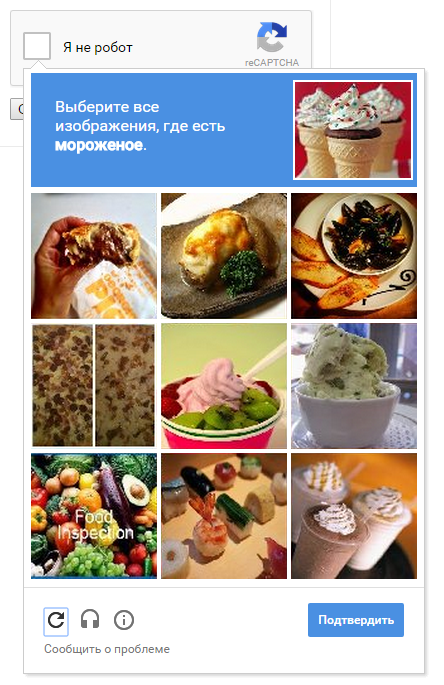
Однако и такая задача кажется решаемой для сверточной сети. Можно предположить, что в будущем возникнут центры регистрации людей, например, человека по скайпу интервьюирует живой человек, проверяет сканы паспортов и тому подобное, затем человеку выдается цифровая подпись, с которой он может автоматически регистрироваться на любом сайте.
© Максим Веденев
