Это седьмая статья из цикла и заключительная в блоке, посвящённом трассировке сигнальных линий. Дальше есть идея развивать проект и выходить на руководство по проектированию печатных плат в виде удобной книги, поэтому по публикациям, возможно. будет пауза. В статье рассматривается важная тема — дифференциальная схема передачи данных, получающая всё большее распространение в современных системах, и предлагаются рекомендации по трассировке дифференциальных пар, позволяющей обеспечить преимущества этой схемы.
В предыдущей было показано, что перекрёстная связь между независимыми сигнальными линиями является источником нежелательных помех. Однако в случае дифференциальной схемы передачи сильная перекрёстная связь, напротив, делает сигнал более устойчивым к помехам. При такой схеме используются две линии (дифференциальная пара), источники сигнала которых находятся в противофазе, а приёмник реагирует на разницу напряжений на линиях VDIFF= V+-V– (рис. 1). Синфазный сигнал (англ. common signal) определяется как VCOMM=1/2∙(V++ V–) и может быть ненулевым, например, как в распространённом стандарте LVDS. Дифференциальная пара характеризуется двумя сопротивлениями:


Вводная теория дифференциальной передачи сигналов описывается во многих источниках, например, в [1]. С точки зрения проектирования печатных плат важно остановиться на преимуществах дифференциальной схемы относительно ассиметричной (англ. single-ended) и на требованиях к топологии дифференциальных пар, эти преимущества обеспечивающие.
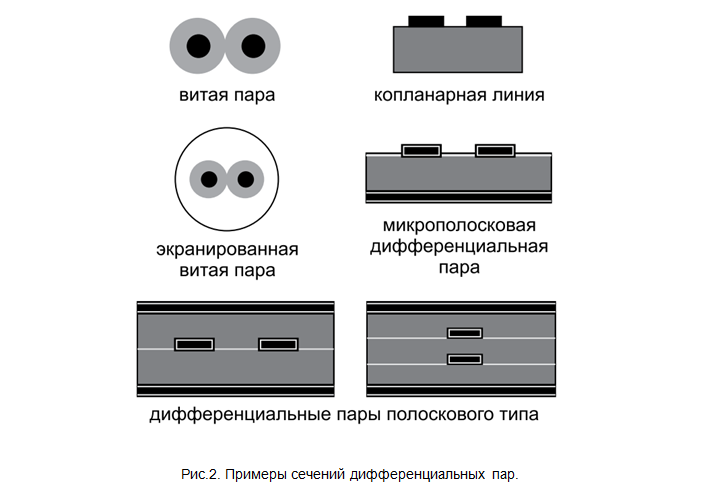
Прежде всего, идеальная дифференциальная пара симметрична, то есть на протяжении всей длины её сечение должно быть неизменным и обладать осью симметрии (рис. 2). Это, так же, как и в случае ассиметричной линии передачи, обеспечивает постоянство волнового сопротивления дифференциальной пары, что значительно снижает отражения в линии и искажения сигнала.
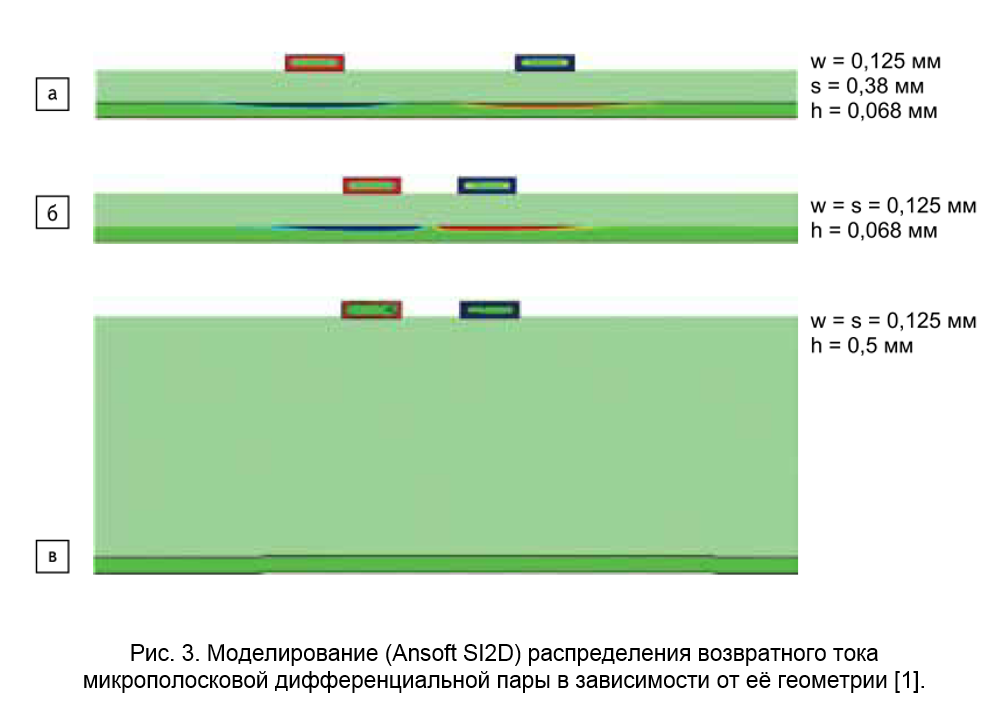
Уменьшения расстояния между линиями до s≤2∙h приводит к значительному увеличению взаимной связи и перекрытию распределений возвратных токов в опорном слое (рис. 3-Б). Такая дифференциальная пара называется дифференциальной парой с сильной взаимной связью (англ. tightly coupled differential line). Дифференциальный импеданс становится в большей степени зависимым от расстояния между дорожками. Его значение снижается, поэтому для сохранения прежнего значения требуются более узкие дорожки, что несколько повышает омические потери. Однако именно такая топология дифференциальной пары обеспечивает следующие преимущества относительно ассиметричной линии:
Указанные преимущества стоит назвать потенциальными преимуществами, потому что в полной мере они реализуются только при одновременном выполнении двух условий:
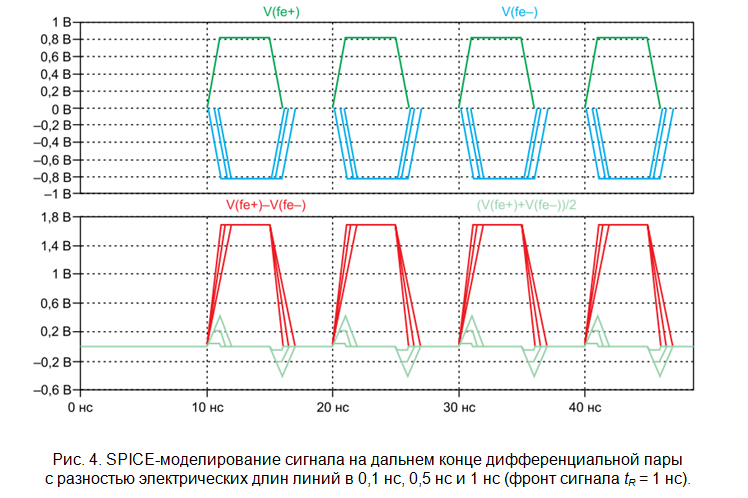
Если не учитывать неидеальность источника сигнала, то выполнение первого требования обеспечивается соблюдением рекомендации Р.1 и согласованием как дифференциального, так и синфазного сигналов на стороне нагрузки. Однако на практике из-за ограничений, накладываемых расположением и геометрией контактных площадок компонентов и переходных отверстий, необходимостью поворотов, строгое постоянство сечения дифференциальной пары труднореализуемо, что выражается также и в разности длин линий пары. Разность длин пары приводит к разбегу фазы, искажая дифференциальный сигнал и создавая помехи синфазного сигнала (рис. 4).
Распространённой практикой выравнивания длин линий (англ. length matching, tuning) является увеличение длины более короткой линий за счёт дополнительных изгибов, которые могут образовывать регулярную структуру (рис. 5). Очевидно, что при этом неизбежно изменяется расстояние между линиями пары. Это в свою очередь приводит к локальному изменению импеданса пары и возникновению отражений. Д. Брукс в одной из статей высказывает мнение, что задача выравнивания длин линий пары имеет бóльшую важность с точки зрения целостности сигналов и ЭМС. А выбор геометрии изгибов не имеет критического значения, с той лишь оговоркой, что длинные и узкие изгибы не рекомендуются, так как могут приводить к искажениям за счёт сильной взаимной связи участков. Однако этот тезис не является универсальным правилом. Дело в том, что существуют и более продвинутая методика выравнивания длин линий, которая заключается в одновременном сохранении импеданса пары в местах изгибов (за счёт изменений ширины линий, применения локальных вырезов в опорном слое и т.п.). Однако построение такой геометрии выравнивания является достаточно сложной задачей, требующей применения специализированных САПР, и оправдана только для гигагерцовых сигнальных линий. Другой вариант – это локальное увеличение расстояния между линиями пары и выравнивание за счёт изгибов на одной из линий. Иными словами, осуществление локального перехода к дифференциальной паре со слабой связью, для которой импеданс не так сильно зависит от расстояния между линиями (что наблюдается в местах изгибов). Примеры и более подробная информация по этим методикам может быть найдена в материалах, представленных на сайте Simberian, Inc.

Критерий достаточной степени равенства длин линий приводится в [1]: «Длины линий дифференциальной пары должны быть выровнены между собой с точностью ∆L<0,1∙tR∙v. Участок выравнивания рекомендуется располагать в той части дифференциальной пары, где симметрия уже нарушена (например, расположением выводов микросхемы)». По аналогии с ассиметричными линиями влияние локальной неоднородности дифференциального импеданса тем меньше, чем меньше электрическая длина участка выравнивания по сравнению с длительностью фронта сигнала.
Задача осложняется тем, что выравнивание прекрасно работает только для полосковой линии, для которой скорости распространения синфазного и дифференциального сигналов равны. Для микрополосковой линии даже идеальное выравнивание длин линий пары не обеспечивает отсутствия искажений, а только является методом их снижения. Но так как полосковая линия требует перехода на внутренние слои с применением переходных отверстий, самих по себе являющихся неоднородностью, то нельзя однозначно сказать, что у микрополосковой линии нет преимуществ. Безусловно, значимость этих эффектов растёт с повышением верхней границы частотной полосы сигнала. И если на частотах ниже 1 ГГц выравнивание обеспечивает низкий уровень искажений, то в области нескольких гигагерц и выше не существует универсальных рекомендаций и задача трассировки решается с помощью моделирования для каждого конкретного случая.
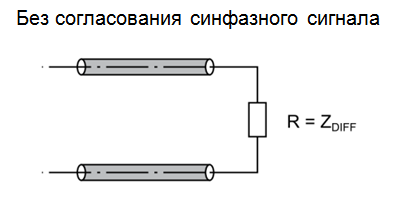
Помехи синфазного сигнала могут возникать как в самой дифференциальной паре из-за любой её несимметричности, так могут и наводиться с других сигнальных линий. Исключить искажения невозможно, однако с помощью согласования линии, которое препятствует возникновению повторных отражений и осцилляций, можно свести к минимуму их последствия. Основные методы согласования дифференциальной пары на дальнем конце представлены в таблице 1. Схема без согласования синфазного сигнала проста и поэтому используется достаточно часто, однако при наличии синфазных помех в линий простота оборачивается потенциальными проблемами. В отличие от дифференциального сигнала, синфазный сигнал является хорошим источником ЭМИ. Особенно синфазные помехи становятся критичными при использовании для передачи сигнала неэкранированной витой пары, поэтому рекомендуется использовать экранированные витые пары и синфазные дроссели на выходе.
Таблица 1. Методы согласования сигнальной линии.
Примечания:
1. При расчёте значений согласующих сопротивлений удобно использовать значения импеданса чётного ZEVEN (англ. even mode) и нечётного ZODD (англ. odd mode) режимов работы дифференциальной пары. По определению это значения импеданса одной из линий в специальных режимах работы, когда сигнал при распространении в дифференциальной паре не искажается. В случае симметричной дифференциальной пары это равные сигналы V+ = V– для чётного режима и противофазные сигналы V+ = –V– для нечётного режима. При этом они связаны со значениями характеристических импедансов дифференциальной пары следующими соотношениями: ZDIFF= 2∙ZODD, ZCOMM=1/2∙ZEVEN.
2. Для дифференциальной пары со слабой взаимной связью ZODD ≈ ZEVEN ≈ Z0 и T-образные схемы согласования вырождаются в параллельную схему согласования каждой из линий.
Дифференциальная схема обладает множеством преимуществ относительно ассиметричной и является основной для надёжных и высокоскоростных стандартов передачи данных, в том числе для систем с большим количеством узлов. С продолжением тенденции роста тактовых частот разработчикам придётся всё чаще сталкиваться с трассировкой дифференциальных пар, поэтому данная компетенция является стратегически важной и должна быть основана не только на общих рекомендациях, а подкреплена результатами моделирования в специализированных САПР и экспериментальными данными.
[1] Bogatin E. «Signal and power integrity — simplified», 2nd ed., Pearson, 2010
Статья была впервые опубликована в журнале «Компоненты и технологии» 2018, №5. Публикация на «Habr» согласована с редакцией журнала.
Вновь обращаюсь к читателям, коих после переезда с «Geektimes» мтало меньше, за обратной связью, которую можно выразить в комментариях, в личных сообщениях, как угодно. Это касается и этой статьи, и всех предыдущих. Хочется сделать крутой удобный справочник-руководство, с помощью которого кто-то успешно стартанёт в проектировании печатных плат с меньшим количеством ошибок, кто-то углубится и повысит их качество. Присоединяйтесь, конструктивно критикуйте, сделаем вклад в развитие отрасли.
В предыдущей было показано, что перекрёстная связь между независимыми сигнальными линиями является источником нежелательных помех. Однако в случае дифференциальной схемы передачи сильная перекрёстная связь, напротив, делает сигнал более устойчивым к помехам. При такой схеме используются две линии (дифференциальная пара), источники сигнала которых находятся в противофазе, а приёмник реагирует на разницу напряжений на линиях VDIFF= V+-V– (рис. 1). Синфазный сигнал (англ. common signal) определяется как VCOMM=1/2∙(V++ V–) и может быть ненулевым, например, как в распространённом стандарте LVDS. Дифференциальная пара характеризуется двумя сопротивлениями:


Вводная теория дифференциальной передачи сигналов описывается во многих источниках, например, в [1]. С точки зрения проектирования печатных плат важно остановиться на преимуществах дифференциальной схемы относительно ассиметричной (англ. single-ended) и на требованиях к топологии дифференциальных пар, эти преимущества обеспечивающие.
Прежде всего, идеальная дифференциальная пара симметрична, то есть на протяжении всей длины её сечение должно быть неизменным и обладать осью симметрии (рис. 2). Это, так же, как и в случае ассиметричной линии передачи, обеспечивает постоянство волнового сопротивления дифференциальной пары, что значительно снижает отражения в линии и искажения сигнала.

Каждой линии дифференциальной пары соответствует своё распределение возвратного тока в опорном слое. Если взаимная связь между линиями пары значительно меньше, чем их связь с опорным слоем, то распределения возвратных токов не пересекаются (рис. 3-А). Такая дифференциальная пара называется дифференциальной парой со слабой взаимной связью (англ. loosly coupled differential line, weak coupling). Так как распределение высокочастотных составляющих сигнала сконцентрировано в опорном слое в области ±3∙h, то практическим критерием для слабой связи является условие, что расстояние между краями печатных дорожек s>6∙h или s>3∙w. Так как дифференциальный импеданс пары со слабой связью практически не зависит от расстояния между дорожками ZDIFF≈2∙Z0, то это расстояние может меняться вдоль длины линии – например, при наличии препятствия на пути дифференциальной пары. Это упрощает требования к топологии дифференциальной пары, однако такие линии лишены основных преимуществ дифференциальной передачи данных.Р.1.
Сечение дифференциальной пары должно быть максимально (в идеале – зеркально) симметрично и однородно на всём её протяжении. Между линиями пары не должно быть элементов топологии других сигнальных цепей.

Уменьшения расстояния между линиями до s≤2∙h приводит к значительному увеличению взаимной связи и перекрытию распределений возвратных токов в опорном слое (рис. 3-Б). Такая дифференциальная пара называется дифференциальной парой с сильной взаимной связью (англ. tightly coupled differential line). Дифференциальный импеданс становится в большей степени зависимым от расстояния между дорожками. Его значение снижается, поэтому для сохранения прежнего значения требуются более узкие дорожки, что несколько повышает омические потери. Однако именно такая топология дифференциальной пары обеспечивает следующие преимущества относительно ассиметричной линии:
- Бóльшая устойчивость дифференциального сигнала к наведённым помехам, в том числе к перекрёстным помехам и помехам в опорном слое. Близкое расположение и симметрия линий приводит к тому, что наведённые помехи на каждую из линий практически равны VNOISE+≈VNOISE-, поэтому дифференциальная помеха мала VNOISEDIFF=VNOISE+-VNOISE-≈0. Эта помеха тем меньше, чем дальше от дифференциальной пары находится её источник.
- Меньший уровень ЭМИ и создаваемых перекрёстных помех. Так как сигналы V+ и V– находятся в противофазе, то излучаемые ими электромагнитные поля примерно равны по величине и имеют противоположное друг другу направление. Это приводит к тому, что суперпозиция полей в дальнем поле стремится к нулю. Тот же эффект значительно снижает создаваемые дифференциальной парой перекрёстные помехи в ближнем поле.
- Меньшее влияние разрывов в опорном слое. Возвратные токи I+ и I– также находятся в противофазе, при этом в силу геометрической симметрии их распределения в опорном слое симметричны. В связи с этим суммарный ток в опорном слое IREF = I+ + I– уменьшается, а в области перекрытия становится равным нулю. В случае полного перекрытия, когда дифференциальная пара находится на удалении от опорного слоя h>2∙(s+w) и взаимная связь линий значительно превышает их связь с опорным слоем, ток в опорном слое отсутствует (рис. 3-В). Такая ситуация может возникать, в частности, когда дифференциальная пара пересекает широкий разрыв в опорном слое. Несмотря на то, что импеданс в месте пересечения претерпевает локальное изменение, искажения дифференциального сигнала малы по сравнению с искажениями ассиметричного сигнала в подобном случае [1].
Указанные преимущества стоит назвать потенциальными преимуществами, потому что в полной мере они реализуются только при одновременном выполнении двух условий:
- строгая противофазность сигналов на всём протяжении линии,
- отсутствие помех синфазного сигнала.
Если не учитывать неидеальность источника сигнала, то выполнение первого требования обеспечивается соблюдением рекомендации Р.1 и согласованием как дифференциального, так и синфазного сигналов на стороне нагрузки. Однако на практике из-за ограничений, накладываемых расположением и геометрией контактных площадок компонентов и переходных отверстий, необходимостью поворотов, строгое постоянство сечения дифференциальной пары труднореализуемо, что выражается также и в разности длин линий пары. Разность длин пары приводит к разбегу фазы, искажая дифференциальный сигнал и создавая помехи синфазного сигнала (рис. 4).

Распространённой практикой выравнивания длин линий (англ. length matching, tuning) является увеличение длины более короткой линий за счёт дополнительных изгибов, которые могут образовывать регулярную структуру (рис. 5). Очевидно, что при этом неизбежно изменяется расстояние между линиями пары. Это в свою очередь приводит к локальному изменению импеданса пары и возникновению отражений. Д. Брукс в одной из статей высказывает мнение, что задача выравнивания длин линий пары имеет бóльшую важность с точки зрения целостности сигналов и ЭМС. А выбор геометрии изгибов не имеет критического значения, с той лишь оговоркой, что длинные и узкие изгибы не рекомендуются, так как могут приводить к искажениям за счёт сильной взаимной связи участков. Однако этот тезис не является универсальным правилом. Дело в том, что существуют и более продвинутая методика выравнивания длин линий, которая заключается в одновременном сохранении импеданса пары в местах изгибов (за счёт изменений ширины линий, применения локальных вырезов в опорном слое и т.п.). Однако построение такой геометрии выравнивания является достаточно сложной задачей, требующей применения специализированных САПР, и оправдана только для гигагерцовых сигнальных линий. Другой вариант – это локальное увеличение расстояния между линиями пары и выравнивание за счёт изгибов на одной из линий. Иными словами, осуществление локального перехода к дифференциальной паре со слабой связью, для которой импеданс не так сильно зависит от расстояния между линиями (что наблюдается в местах изгибов). Примеры и более подробная информация по этим методикам может быть найдена в материалах, представленных на сайте Simberian, Inc.

Критерий достаточной степени равенства длин линий приводится в [1]: «Длины линий дифференциальной пары должны быть выровнены между собой с точностью ∆L<0,1∙tR∙v. Участок выравнивания рекомендуется располагать в той части дифференциальной пары, где симметрия уже нарушена (например, расположением выводов микросхемы)». По аналогии с ассиметричными линиями влияние локальной неоднородности дифференциального импеданса тем меньше, чем меньше электрическая длина участка выравнивания по сравнению с длительностью фронта сигнала.
Задача осложняется тем, что выравнивание прекрасно работает только для полосковой линии, для которой скорости распространения синфазного и дифференциального сигналов равны. Для микрополосковой линии даже идеальное выравнивание длин линий пары не обеспечивает отсутствия искажений, а только является методом их снижения. Но так как полосковая линия требует перехода на внутренние слои с применением переходных отверстий, самих по себе являющихся неоднородностью, то нельзя однозначно сказать, что у микрополосковой линии нет преимуществ. Безусловно, значимость этих эффектов растёт с повышением верхней границы частотной полосы сигнала. И если на частотах ниже 1 ГГц выравнивание обеспечивает низкий уровень искажений, то в области нескольких гигагерц и выше не существует универсальных рекомендаций и задача трассировки решается с помощью моделирования для каждого конкретного случая.
Помехи синфазного сигнала могут возникать как в самой дифференциальной паре из-за любой её несимметричности, так могут и наводиться с других сигнальных линий. Исключить искажения невозможно, однако с помощью согласования линии, которое препятствует возникновению повторных отражений и осцилляций, можно свести к минимуму их последствия. Основные методы согласования дифференциальной пары на дальнем конце представлены в таблице 1. Схема без согласования синфазного сигнала проста и поэтому используется достаточно часто, однако при наличии синфазных помех в линий простота оборачивается потенциальными проблемами. В отличие от дифференциального сигнала, синфазный сигнал является хорошим источником ЭМИ. Особенно синфазные помехи становятся критичными при использовании для передачи сигнала неэкранированной витой пары, поэтому рекомендуется использовать экранированные витые пары и синфазные дроссели на выходе.
Таблица 1. Методы согласования сигнальной линии.
| Название и схема | Уровень потерь | Комментарии |
|---|---|---|
 |
низкий |  |
 |
высокий |  |
 |
высокий |  |
 |
средний |  |
Примечания:
1. При расчёте значений согласующих сопротивлений удобно использовать значения импеданса чётного ZEVEN (англ. even mode) и нечётного ZODD (англ. odd mode) режимов работы дифференциальной пары. По определению это значения импеданса одной из линий в специальных режимах работы, когда сигнал при распространении в дифференциальной паре не искажается. В случае симметричной дифференциальной пары это равные сигналы V+ = V– для чётного режима и противофазные сигналы V+ = –V– для нечётного режима. При этом они связаны со значениями характеристических импедансов дифференциальной пары следующими соотношениями: ZDIFF= 2∙ZODD, ZCOMM=1/2∙ZEVEN.
2. Для дифференциальной пары со слабой взаимной связью ZODD ≈ ZEVEN ≈ Z0 и T-образные схемы согласования вырождаются в параллельную схему согласования каждой из линий.
Дифференциальная схема обладает множеством преимуществ относительно ассиметричной и является основной для надёжных и высокоскоростных стандартов передачи данных, в том числе для систем с большим количеством узлов. С продолжением тенденции роста тактовых частот разработчикам придётся всё чаще сталкиваться с трассировкой дифференциальных пар, поэтому данная компетенция является стратегически важной и должна быть основана не только на общих рекомендациях, а подкреплена результатами моделирования в специализированных САПР и экспериментальными данными.
Литература
[1] Bogatin E. «Signal and power integrity — simplified», 2nd ed., Pearson, 2010
Статья была впервые опубликована в журнале «Компоненты и технологии» 2018, №5. Публикация на «Habr» согласована с редакцией журнала.
P.S.
Вновь обращаюсь к читателям, коих после переезда с «Geektimes» мтало меньше, за обратной связью, которую можно выразить в комментариях, в личных сообщениях, как угодно. Это касается и этой статьи, и всех предыдущих. Хочется сделать крутой удобный справочник-руководство, с помощью которого кто-то успешно стартанёт в проектировании печатных плат с меньшим количеством ошибок, кто-то углубится и повысит их качество. Присоединяйтесь, конструктивно критикуйте, сделаем вклад в развитие отрасли.
