How to become an author
Search
Write a publication
Pull to refresh
Company grade from Habr Career
3.73
Grade
322.43
Rating
VK
Building the Internet

Обзор задач по алгоритмам для собеседований — генерация множеств

Reading time7 min
Views64K
VK corporate blogIT-emigrationPython*Algorithms*IT career
From sandbox

Привет, Хабр!


Этим постом начинается разбор задачек по алгоритмам, которые крупные IT-компании (Mail.Ru Group, Google и т.п.) так любят давать кандидатам на собеседованиях (если плохо пройти собеседование по алгоритмам, то шансы устроиться на работу в компанию мечты, увы, стремятся к нулю). В первую очередь этот пост полезен для тех, кто не имеет опыта олимпиадного программирования или тяжеловесных курсов по типу ШАДа или ЛКШ, в которых тематика алгоритмов разобрана достаточно серьезно, или же для тех, кто хочет освежить свои знания в какой-то определенной области.


При этом нельзя утверждать, что все задачи, которые здесь будут разбираться, обязательно встретятся на собеседовании, однако подходы, с помощью которых такие задачи решаются, в большинстве случаев похожи.



Повествование будет разбито на разные темы, и начнем мы с генерирования множеств с определенной структурой.


1. Начнем с баян-баяныча: нужно сгенерировать все правильные скобочные последовательности со скобками одного вида (что такое правильная скобочная последовательность), где количество скобок равно k.


Эту задачу можно решить несколькими способами. Начнем с рекурсивного.


В этом способе предполагается, что мы начинаем перебирать последовательности с пустого списка. После того, как в список добавлена скобка (открывающая или закрывающая), снова выполняется вызов рекурсии и проверка условий. Какие могут быть условия? Необходимо следить за разницей между открывающими и закрывающими скобками (переменная cnt) — нельзя добавить закрывающую скобку в список, если эта разница не является положительной, иначе скобочная последовательность перестанет быть правильной. Осталось аккуратно реализовать это в коде.


k = 6 # количество скобок
init = list(np.zeros(k)) # пустой список, куда кладем скобки
cnt = 0 # разница между скобками
ind = 0 # индекс, по которому кладем скобку в список 

def f(cnt, ind, k, init):
    # кладем откр. скобку, только если хватает места
    if (cnt <= k-ind-2):
        init[ind] = '('
        f(cnt+1, ind+1, k, init)
    # закр. скобку можно положить всегда, если cnt > 0
    if cnt > 0:
        init[ind] = ')'
        f(cnt-1, ind+1, k, init)
    # выходим из цикла и печатаем
    if ind == k:
        if cnt == 0:
            print (init)

Сложность этого алгоритма — $O((C_k^{k/2} - C_k^{k/2 -1})*k)$, дополнительной памяти требуется $O(k)$.


При заданных параметрах вызов функции $f(cnt, ind, k, init)$ выведет следующее:



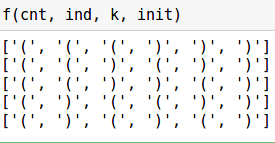
Итеративный способ решения этой задачи: в этом случае идея будет принципиально другой — нужно ввести понятие лексикографического порядка для скобочных последовательностей.


Все правильные скобочные последовательности для одного типа скобок можно упорядочить с учётом того, что $'('<')'$. Например, для n=6 самой лексикографически младшей последовательностью будет $((()))$, а самой старшей — $()()()$.


Чтобы получить следующую лексикографическую последовательность, нужно найти самую правую открывающуюся скобку, перед которой стоит закрывающаяся, чтобы при их перестановке местами скобочная последовательность оставалась правильной. Поменяем их местами и сделаем суффикс самым лексикографическим младшим — для этого нужно на каждом шаге вычислять разницу между количеством скобок.


На мой взгляд, этот подход чуть муторнее рекурсивного, однако его можно использовать для решения других задач на генерирование множеств. Реализуем это в коде. 


# количество скобок, должно быть четное
n = 6
arr = ['(' for  _ in range(n//2)] + [')' for _ in range(n//2)]

def f(n, arr):
    # печатаем нулевую последовательность
    print (arr)
    while True:
        ind = n-1
        cnt = 0
        # находим откр. скобку, которую можно заменить
        while ind>=0:
            if arr[ind] == ')':
                cnt -= 1
            if arr[ind] == '(':
                cnt += 1
            if cnt < 0 and arr[ind] =='(':
                break
            ind -= 1
        # если не нашли, то алгоритм заканчивает работу
        if ind < 0:
            break
        # заменяем на закр. скобку
        arr[ind] = ')'
        # заменяем на самую лексикографическую минимальную
        for i in range(ind+1,n):
            if i <= (n-ind+cnt)/2 +ind:
                arr[i] = '('
            else:
                arr[i] = ')'
        print (arr)

Сложность этого алгоритма такая же, как и в прошлом примере.


Кстати, есть несложный способ, который демонстрирует, что количество сгенерированных скобочных последовательностей для данного n/2 должно совпадать с числами Каталана.



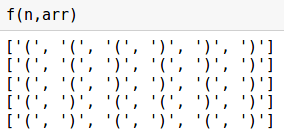
Работает!


Отлично, со скобками пока всё, теперь перейдем к генерированию подмножеств. Начнем с простой задачки.


2. Дан упорядоченный по возрастанию массив с числами от $0$ до $n-1$, требуется сгенерировать все его подмножества.


Заметим, что количество подмножеств такого множества равно в точности $2^n$. Если каждое подмножество представить в виде массива индексов, где $0$ означает, что элемент не входит в множество, а $1$ — что входит, тогда генерирование всех таких массивов будет являться генерированием всех подмножеств.


Если рассмотреть побитовое представление чисел от 0 до $2^n - 1$, то они будут задавать искомые подмножества. То есть для решения задачи необходимо реализовать прибавление единицы к двоичному числу. Начинаем со всех нулей и заканчиваем массивом, в котором одни единицы.


n = 3
B = np.zeros(n+1) # массив B берем на 1 длиннее (для удобства выхода из цикла)
a = np.array(list(range(n))) # изначальный массив

def f(B, n, a):
    # начинаем цикл
    while B[0] == 0:
        ind = n 
        # ищем самый правый ноль
        while B[ind] == 1:
            ind -= 1
        # заменяем на 1
        B[ind] = 1
        # на все остальное пишем нули
        B[(ind+1):] = 0
        print (a[B[1:].astype('bool')])

Сложность этого алгоритма — $O(n*2^n)$, по памяти — $O(n)$.


Посмотрим на вывод.


Теперь чуть-чуть усложним предыдущую задачу.


3. Дан упорядоченный массив по возрастанию с числами от $0$ до $n-1$, требуется сгенерировать все его $k$-элементные подмножества (решить итеративным способом).


Замечу, что по формулировке эта задача похожа на предыдущую и решать её можно с помощью примерно такой же методики: взять изначальный массив с $k$ единицами и $n-k$ нулями и последовательно перебрать все варианты таких последовательностей длиной $n.$


Однако требуются небольшие изменения. Нам нужно перебрать все $k$-значные наборы чисел от $0$ до $n-1$. Необходимо понять, как именно нужно перебирать подмножества. В данном случае можно ввести понятие лексикографического порядка для таких множеств.


Также упорядочим последовательность по кодам символов: $1 < 0$ (это, конечно, странно, но так надо, и сейчас поймем, почему). Например, для $n=4, k=2$ самой младшей и старшей будут последовательности $[1,1,0,0]$ и $[0,0,1,1]$.


Осталось понять, как описать переход от одной последовательности к другой. Тут всё просто: если меняем $1$ на $0$, то слева пишем лексикографически минимальное с учетом сохранения условия на $k$. Код:


n = 5
k = 3
a = np.array(list(range(n)))

# начальный список первого k - элементного подмножества
init = [1 for _ in range(k)] + [0 for _ in range(n-k)] 

def f(a, n, k, init):
    # печатаем нулевое k-элементное множество
    print (a[a[init].astype('bool')])
    while True:
        unit_cnt = 0
        cur_ind = 0
        # находим нулевой индекс, который будем менять на 1
        while (cur_ind < n) and (init[cur_ind]==1 or unit_cnt==0):
            if init[cur_ind] == 1:
                unit_cnt += 1
            cur_ind += 1
        # если не нашли и дошли до конца - то все сгенерировали
        if cur_ind == n:
            break
        # меняем
        init[cur_ind] = 1
        # заполняем слева лекс. наим. способом
        for i in range(cur_ind):
            if i < unit_cnt-1:
                init[i] = 1
            else:
                init[i] = 0
        print (a[a[init].astype('bool')])

Пример работы:



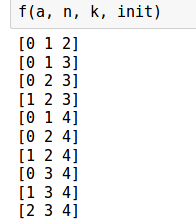
Сложность этого алгоритма — $O(C_n^k * n)$, по памяти — $O(n)$.


4. Дан упорядоченный по возрастанию массив с числами от $0$ до $n-1$, требуется сгенерировать все его $k$-элементные подмножества (решить рекурсивно).


Теперь попробуем рекурсию. Идея простая: на этот раз обойдемся без описания, смотрите код.


n = 5
a = np.array(list(range(n)))
ind = 0 # число, в котором лежит количество элементов массива
num = 0 # индекс, с которого начинается новый вызов функции
k = 3
sub = list(-np.ones(k)) # подмножество

def f(n, a, num, ind, k, sub):
    # если уже k единиц есть, то печатем и выходим
    if ind == k:
        print (sub)
    else:
        for i in range(n - num):
            # вызываем рекурсию, только если можем добрать до k единиц
            if (n - num - i >= k - ind):
                # кладем в этот индекс элемент
                sub[ind] = a[num + i]
                # обратите внимание на аргументы
                f(n, a, num+1+i, ind+1, k, sub)

Пример работы:


Сложность такая же, как и у прошлого способа.


5. Дан упорядоченный по возрастанию массив с числами от $0$ до $n-1$, требуется сгенерировать все его перестановки.


Будем решать с помощью рекурсии. Решение похожа на предыдущее, где у нас есть вспомогательный список. Изначально он нулевой, если на $i$-ом месте элемента стоит единица, то элемент $i$ уже есть в перестановке. Сказано — сделано:


a = np.array(range(3))
n = a.shape[0]
ind_mark = np.zeros(n) # массив индексов
perm = -np.ones(n) # уже заполненная часть перестановки

def f(ind_mark, perm, ind, n):
    if ind == n:
        print (perm)
    else:
        for i in range(n):
            if not ind_mark[i]:
                # кладем в перестановку элемент
                ind_mark[i] = 1
                # заполняем индекс
                perm[ind] = i
                f(ind_mark, perm, ind+1, n)
                # важный момент - нужно занулить индекс
                ind_mark[i] = 0

Пример работы:



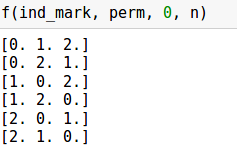
Сложность этого алгоритма — $O(n^2 *n!)$, по памяти — $O(n).$


Теперь рассмотрим две очень интересных задачки на коды Грея. Если в двух словах, то это набор последовательностей одной длины, где каждая последовательность отличается от своих соседей в одном разряде.


6. Сгенерировать все двумерные коды Грея длиной n.


Идея решения этой задачи классная, но если не знать решения, то бывает очень сложно додуматься. Замечу, что количество таких последовательностей равно $2^n$.


Будем решать итеративно. Пусть мы сгенерировали какую-то часть таких последовательностей и они лежат в каком-то списке. Если мы продублируем такой список и запишем его в обратном порядке, то последняя последовательность в первом списке совпадает с первой последовательностью во втором списке, предпоследняя совпадает со второй и т.д. Соединим эти списки в один.


Что необходимо сделать, чтобы все последовательности в списке отличались друг от друга в одном разряде? Поставить в соответствующих местах одну единицу в элементы второго списка, чтобы получить коды Грея.


Это сложно воспринять «на слух», изобразим итерации этого алгоритма. 



n = 3
init = [list(np.zeros(n))]

def f(n, init):
    for i in range(n):
        for j in range(2**i):
            init.append(list(init[2**i - j - 1]))
            init[-1][i] = 1.0
    return init

Сложность этой задачи — $O(n*2^n)$, по памяти такая же.


Теперь усложним задачу.


7. Сгенерировать все k-мерные коды Грея длиной n.


Понятно, что прошлая задача является лишь частным случаем этой задачи. Однако тем красивым способом, которым была решена прошлая задача, эту решить не получится, здесь необходимо перебирать последовательности в правильном порядке. Заведем двумерный массив $k*n$. Изначально в последней строчке стоят единицы, а в остальных стоят нули. При этом в матрице также могут встречаться и $-1$. Здесь $1$ и $-1$ отличаются друг от друга направлением: $1$ указывает вверх, $-1$ указывает вниз. Важно: в каждом столбике в любой момент времени может быть только одна $1$ или $-1$, а остальные числа будут нулями.



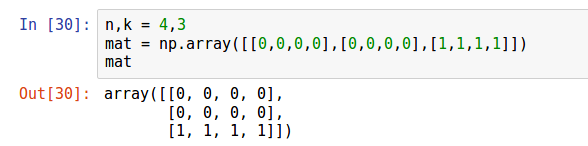
Теперь поймем, каким именно образом можно перебрать эти последовательности, чтобы получались коды Грея. Начинаем с конца двигать элемент вверх.



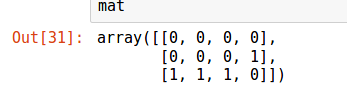
На следующем шаге мы упремся в потолок. Записываем получившуюся последовательность. После достижения предела необходимо начать работать со следующим столбцом. Искать его нужна справа налево, и если мы нашли столбец, который можно двигать, то у всех столбцов, с которыми мы не могли работать, стрелочки поменяются в противоположном направлении, чтобы их опять можно было двигать.



Теперь можно двигать первый столбец вниз. Двигаем его до тех пор, пока он не упрется в пол. И так далее, пока все стрелочки не упрутся в пол или потолок и не останется столбцов, которые можно двигать.


Однако, в рамках экономии памяти, будем решать эту задачу с помощью двух одномерных массивов длины $n$: в одном массиве будут лежать сами элементы последовательности, а в другом их направления (стрелочки). 


n,k = 3,3
arr = np.zeros(n)
direction = np.ones(n) # один указывает вверх, ноль указывает вниз

def k_dim_gray(n,k):
    # печатаем нулевую последовательность
    print (arr)
    while True:
        ind = n-1
        while ind >= 0:
            # условие на нахождение столбца, который можно двигать
            if (arr[ind] == 0 and direction[ind] == 0) or (arr[ind] == k-1 and direction[ind] == 1):
                direction[ind] = (direction[ind]+1)%2
            else:
                break
            ind -= 1
        # если не нашли такого столбца, то алгоритм закончил работу
        if ind < 0:
            break
        # либо двигаем на 1 вперед, либо на 1 назад
        arr[ind] += direction[ind]*2 - 1
        print (arr)

Пример работы:



Сложность алгоритма — $O(n*k^n)$, по памяти — $O(n)$.


Корректность данного алгоритма доказывается индукцией по $n$, здесь я не будут описывать доказательство.


В следующем посте будем разбирать задачки на динамику.

Tags:
Hubs:
Total votes 28: ↑28 and ↓0+28
Comments15
VK
Building the Internet
36
Karma
0
Rating
Артем Хапкин @temkahap

Программист-исследователь

Send message
WebsiteWebsite

Articles

Information

Website
vk.com
Registered
Founded
Employees
5,001–10,000 employees
Location
Россия
Representative
Миша Берггрен

Your account

Sections

Information

Services

Support
© 2006–2024, Habr