Графика в Julia. Странные паттерны, отражение треугольника от прямой и построение нормалей сферического кота в вакууме

Продолжаем знакомство с очень молодым, но невероятно красивым и мощным языком программирования Julia. Шестилетняя бета наконец-таки закончилась, так что теперь можно не бояться изменений синтаксиса. И пока все спорят, хорошо или плохо начинать индексацию с единицы, взбудораженное сообщество активно закопошилось: выходят новые библиотеки, старые обновляются, стартуют серьёзные проекты, и в университетах этому языку активно учат студентов. Так не будем же отставать! Завариваем чай покрепче, потому что этой ночью будем кодить!

Подготовка к работе

Здесь есть небольшой обзор на русском, так же на хабре имеется знакомство с языком и руководство по установке. Опять же, заостряю внимание на необходимости наличия Windows Management Framework, не то будут проблемы с загрузкой пакетов.

В комплектацию JuliaPRO после обновления теперь входит только Juno. Но лично мне больше нравится Jupyter: с ним не было проблем на ноутбуке, плюс удобно работать в браузере и тут же создавать заметки и формулы, в общем, идеально для создания отчетов, слайдов или методичек.

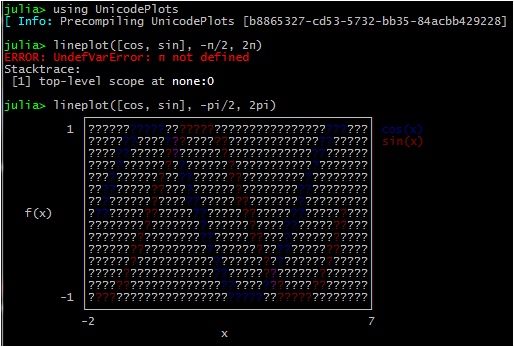
Для Julia существует несколько пакетов, самые же успешные из них входят в Plots в виде бэкэндов. Plots.jl — метаязык построения графика: то есть интерфейс для различных библиотек графиков. Таким образом Plots.jl на самом деле просто интерпретирует ваши команды, а затем создает графики с использованием какой-либо библиотеки графиков. Эти фоновые графические библиотеки называются бэкэндами. Самое приятное состоит в том, что вы можете использовать множество разных графических библиотек с синтаксисом Plots.jl, и мы также увидим, что Plots.jl добавляет новые функции в каждую из этих библиотек!

# Pkg.add("Plots") # так добавлили пакеты до версии 0.7.0
julia>]
pkg>add Plots
pkg>add GR
pkg>add PyPlot
pkg>add Gadfly
pkg>add PlotlyJS
pkg>add UnicodePlots

Бесконечный узор на основе простых чисел

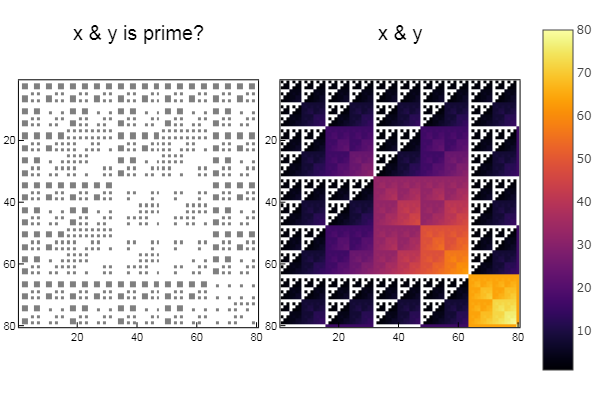
Реализована идея статьи на хабре. В нескольких словах: что если брать координату точки и между абсциссой и ординатой применять какую-нибудь операцию, скажем, XOR или побитовое AND, а затем проверять число на простоту или на принадлежность к числам Фибоначчи, и при положительном ответе закрашивать точку в один цвет, а при отрицательном в другой? Проверим:

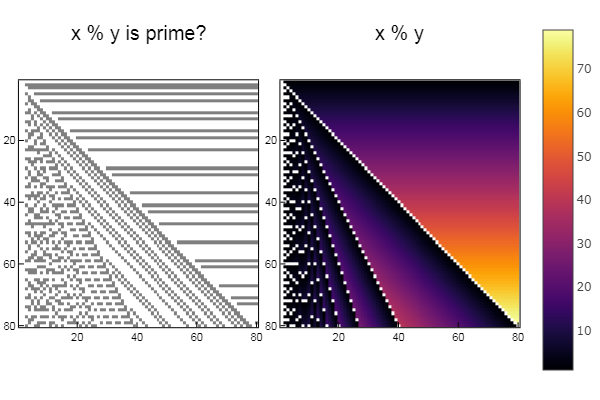
using Plots
plotlyjs()

function eratosphen(n, lst) # решето Эратосфена
    ar = [i for i=1:n]
    ar[1] = 0
    for i = 1:n
        if ar[i] != 0
            push!(lst, ar[i])
            for j = i:i:n
                ar[j] = 0
            end
        end
    end
end

ertsfn = []
eratosphen(1000, ertsfn)
# print(ertsfn)
# print( size(ertsfn) ) # -> 168
N = 80
M = 80

W1 = [in( x % y, ertsfn) for x = 1:N, y = 1:M];
W2 = [x % y for x = 1:N, y = 1:M];
p1 = spy(W1, title = "x % y is prime?")
p2 = spy(W2, title = "x % y")
plot(p1, p2, layout=(2),legend=false)

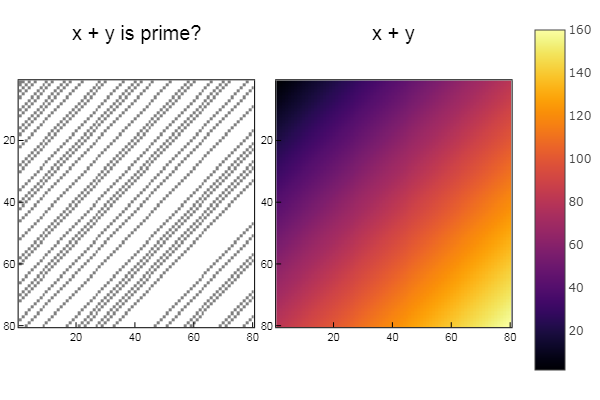
W1 = [in( x + y, ertsfn) for x = 1:N, y = 1:M];
W2 = [x + y for x = 1:N, y = 1:M];
p1 = spy(W1, title = "x + y is prime?")
p2 = spy(W2, title = "x + y")
plot(p1, p2, layout=(2),legend=false)

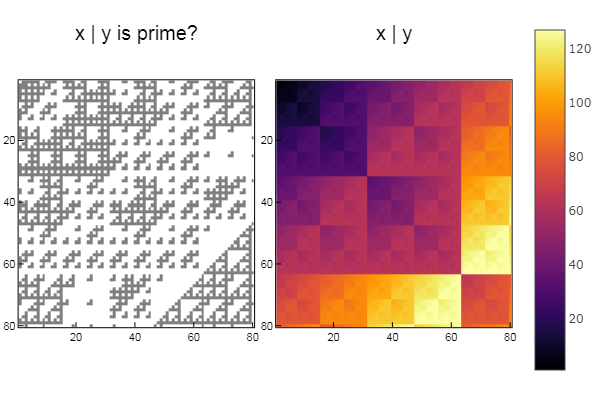
W1 = [in( x | y, ertsfn) for x = 1:N, y = 1:M];
W2 = [x | y for x = 1:N, y = 1:M];
p1 = spy(W1, title = "x | y is prime?")
p2 = spy(W2, title = "x | y")
plot(p1, p2, layout=(2),legend=false)

W1 = [in( x & y, ertsfn) for x = 1:N, y = 1:M];
W2 = [x & y for x = 1:N, y = 1:M];
p1 = spy(W1, title = "x & y is prime?")
p2 = spy(W2, title = "x & y")
plot(p1, p2, layout=(2),legend=false)

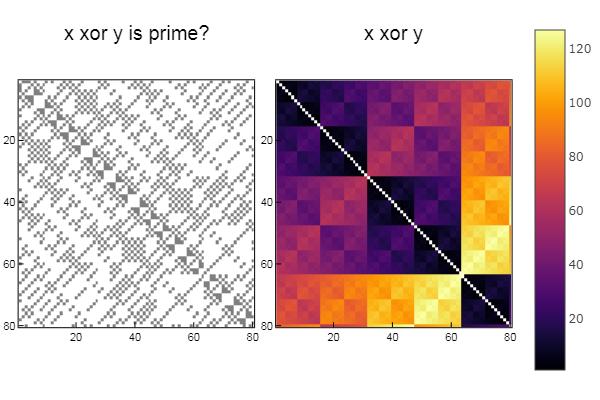
W1 = [in( xor(x, y), ertsfn) for x = 1:N, y = 1:M];
W2 = [xor(x, y) for x = 1:N, y = 1:M];
p1 = spy(W1, title = "x xor y is prime?")
p2 = spy(W2, title = "x xor y")
plot(p1, p2, layout=(2),legend=false)

function fib(n)
    a = 0
    b = 1
    for i = 1:n
        a, b = b, a + b
    end
    return a
end
fbncc = fib.( [i for i=1:10] )

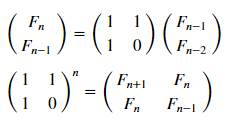
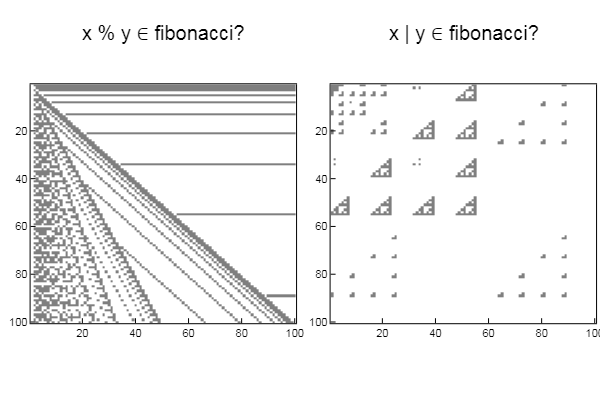
matr_fib = n -> [1 1; 1 0]^(n-1) #  анонимная функция, возводящая матрицу в степень n-1
mfbnc = [ matr_fib( i )[1,1] for i=1:17]; # элемент 1,1 этой матрицы есть n-й элемент множества Фибоначчи
N = 100
M = N

W1 = [in( x % y, mfbnc) for x = 1:N, y = 1:M];
W2 = [in( x | y, mfbnc) for x = 1:N, y = 1:M];
p1 = spy(W1, title = "x % y ∈ fibonacci?")
p2 = spy(W2, title = "x | y ∈ fibonacci?")
plot(p1, p2, layout=(2),legend=false)

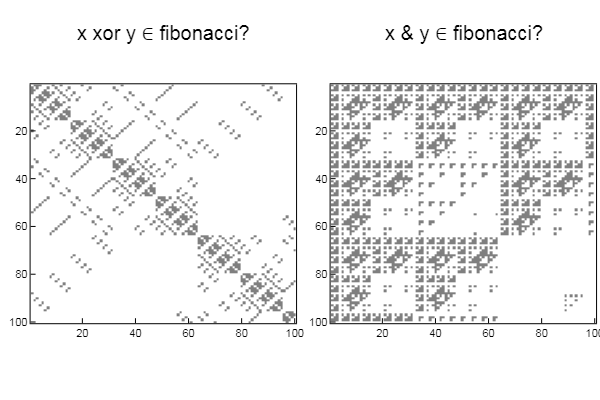
W1 = [in( xor(x, y), mfbnc) for x = 1:N, y = 1:M];
W2 = [in( x & y, mfbnc) for x = 1:N, y = 1:M];
p1 = spy(W1, title = "x xor y ∈ fibonacci?")
p2 = spy(W2, title = "x & y ∈ fibonacci?")
plot(p1, p2, layout=(2),legend=false)

Отражение фигуры относительно прямой

Данный вид отображения определяется матрицей:

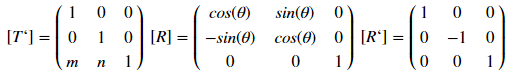
где [T'], [R] и [R'] соответственно матрицы перемещения, поворота и отражения. Как это работает? Разберем на примере смещения — для точки с координатами (х, у) смещение на m по иксу и на n по игреку буде определяться преобразованием:

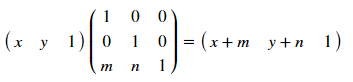
Эти матрицы позволяют проводить преобразования для различных многоугольников, главное записывать друг под дружкой координаты и не забывать про столбец единиц в конце. Таким образом [T]:

• смещает прямую в началу координат вместе с преобразуемым многоугольником
• поворачивает её до совпадения с осью Х
• отражает все точки многоугольника относительно Х
• затем следует обратный поворот и перенос

Более детально тема раскрыта в книге Роджерс Д., Адамс Дж. Математические основы машинной графики

А теперь закодим это!

using Plots
plotlyjs()
f = x -> 0.4x + 2 # функция задающая прямую
# иксы и игреки транспонируем в столбцы
X = [2 4 2 2]'
Y = [4 6 6 4]'
xs = [-2; 7] # отрезок принадлежащий прямой
ys = f(xs)
inptmtrx = [ X Y ones( size(X, 1), 1 ) ] # приписываем столбец единиц

m = 0
n = -f(0) # смещение по Y
displacement = [1 0 0; 0 1 0; m n 1]

a = (ys[2]-ys[1]) / (xs[2]-xs[1]) # тангенс угла наклона прямой
θ = -atan(a)
rotation = [cos(θ) sin(θ) 0; -sin(θ) cos(θ) 0; 0 0 1]
reflection = [1 0 0; 0 -1 0; 0 0 1]

T = displacement * rotation * reflection * rotation^(-1) * displacement^(-1) # полная матрица преобразования
outptmtrx = inptmtrx * T
plot( X, Y)
plot!( xs, ys )
plot!( outptmtrx[:,1], outptmtrx[:,2] )

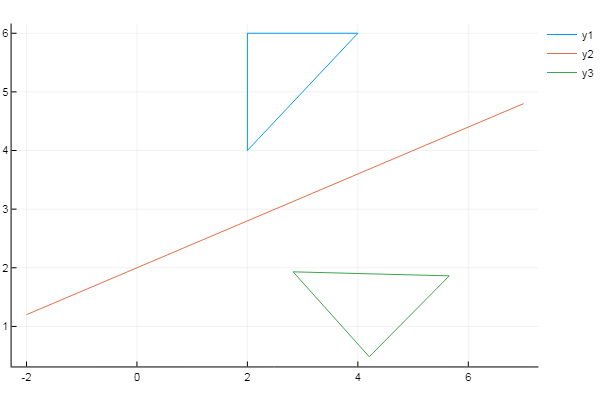
Занимательный факт: если избавиться от греческих символов и заменить первую строку на

function y=f(x,t)
    y=0.4*x + 2
endfunction,

скобки [ ] обрамляющие индексы массивов на ( ), а плоты на plot( X, Y, xs, ys, trianglenew(:,1), trianglenew(:,2) ), то данный код вполне-таки запускается в Scilab.

Работа с трехмерной графикой

Некоторые из перечисленных пакетов поддерживают построение трехмерных графиков. Но отдельно хотелось бы отметить довольно мощное средство визуализации Makie, работающий в купе с пакетами GLFW и GLAbstraction реализующими возможности OpenGL в julia. Больше информации о Makie. Его апробацию спрячем под

using Makie

N = 51
x = linspace(-2, 2, N)
y = x
z = (-x .* exp.(-x .^ 2 .- (y') .^ 2)) .* 4

scene = wireframe(x, y, z)
xm, ym, zm = minimum(scene.limits[])
scene = surface!(scene, x, y, z)
contour!(scene, x, y, z, levels = 15, linewidth = 2, transformation = (:xy, zm))
scene

wireframe(Makie.loadasset("cat.obj"))

using FileIO

scene = Scene(resolution = (500, 500))
catmesh = FileIO.load(Makie.assetpath("cat.obj"), GLNormalUVMesh)
mesh(catmesh, color = Makie.loadasset("diffusemap.tga"))

x = Makie.loadasset("cat.obj")
mesh(x, color = :black)
pos = map(x.vertices, x.normals) do p, n
    p => p .+ (normalize(n) .* 0.05f0)
end
linesegments!(pos, color = :blue)

На этом с графикой всё. Интерактивность, анимация, 3d, большие данные или быстрое построение простейших графиков — постоянно развивающиеся пакеты удовлетворят почти любой вкус и потребности, к тому же, всё весьма легко осваивается. Смело качаем практические задания и продолжает постигать Julia!

UPD: Все вышепредставленные листинги выполнены в Jupyter с julia 0.6.4. К сожалению некоторые функции метапакета Plots либо убрали либо переименовали, так что продолжаем следить за обновлениями, а пока на скорую руку spy вполне заменяется:

julia> using GR
julia> Z = [x | y for x = 1:40, y = 1:40];
julia> heatmap(Z)