Тема latency со временем становится интересной в разных системах в Яндексе и не только. Происходит это по мере того, как в этих системах появляются какие-либо гарантии по обслуживанию. Очевидно, дело в том, что важно не только пообещать какую-то возможность пользователям, но и гарантировать её получение с разумным временем отклика. «Разумность» времени отклика, конечно, сильно различается для разных систем, но базовые принципы, по которым во всех системах проявляется латентность, — общие, и их вполне можно рассматривать в отрыве от конкретики.
Меня зовут Сергей Трифонов, я работаю в команде Real-Time Map Reduce в Яндексе. Мы разрабатываем платформу для обработки потока данных в реальном времени с секундным и субсекундным временем отклика. Платформа доступна для внутренних пользователей и позволяет им выполнять прикладной код над постоянно поступающими потоками данных. Я попытаюсь сделать краткий обзор основных концепций человечества на тему анализа latency за последние сто десять лет, и сейчас мы попробуем понять, что именно про latency можно узнать, применяя теорию массового обслуживания.
Феномен латентности начали систематически исследовать, насколько мне известно, в связи с появлением систем массового обслуживания — телефонных сетей связи. Теория массового обслуживания началась с работы А. К. Эрланга 1909 г., в которой он показал, что пуассоновское распределение применимо к случайному телефонному трафику. Эрланг разработал теорию, которая многие десятилетия использовалась для проектирования телефонных сетей. Теория позволяет определить вероятность отказа в обслуживании. Для телефонных сетей с коммутацией каналов отказ происходил, если все каналы заняты и звонок не может быть совершён. Вероятность этого события нужно было контролировать. Хотелось иметь гарантию, что, например, 95% всех звонков будут обслужены. Формулы Эрланга позволяют определить, сколько нужно серверов для выполнения этой гарантии, если известна длительность и число звонков. По сути, эта задача как раз про гарантии качества, и сегодня люди по-прежнему решают похожие задачи. Но системы стали гораздо сложнее. Основная проблема теории массового обслуживания в том, что в большинстве институтов её не преподают, и мало кто понимает вопрос за пределами обычной очереди M/M/1 (см. про нотацию ниже), зато хорошо известно, что жизнь намного сложнее этой системы. Поэтому я предлагаю, минуя M/M/1, перейти сразу к самому интересному.
Если не пытаться обрести полное знание о распределении вероятностей в системе, а сосредоточиться на более простых вопросах, можно получить интересные и полезные результаты. Самый известный из них — это, конечно, теорема Литтла. Она применима к системе с любым входным потоком, внутренним устройством любой сложности и произвольным планировщиком внутри. Единственное требование в том, что система должна быть стабильна: должны существовать средние значения времени отклика и длины очереди, тогда они связаны простым выражением
— среднее по времени число запросов в рассматриваемой части системы [шт.], 
— среднее время, за которое запросы проходят через данную часть системы [с], 
— скорость поступления запросов в систему [шт./с]. Сила теоремы в том, что её можно применять к любой части системы: очередь, исполнитель, очередь + исполнитель или сеть целиком. Часто этой теоремой пользуются примерно так: «К нам льётся поток 1Gbit/s, а среднее время отклика мы измерили, и оно составляет 10 мс, следовательно в полёте у нас в среднем 1.25 MB». Так вот, это вычисление не верно. Точнее, верно, только если все запросы имеют одинаковый размер в байтах. Теорема Литтла считает запросы в штуках, а не в байтах.
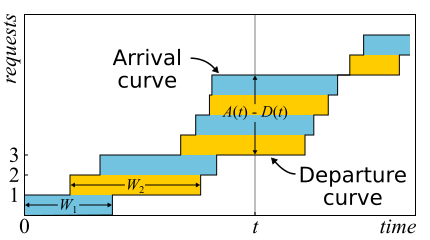В математике часто бывает нужно изучить доказательство, чтобы получить настоящий insight. Это как раз такой случай. Теорема Литтла настолько хороша, что я приведу здесь набросок доказательства. Входящий трафик описывается функцией 
— число запросов, которые вошли в систему к моменту времени 
. Аналогично 
— число запросов, которые вышли из системы к моменту времени . Моментом входа (выхода) запроса считается момент получения (передачи) последнего его байта. Границы системы определяются лишь этими моментами времени, поэтому теорема получается широко применимой. Если нарисовать графики этих функций в одних осях, то легко увидеть, что 
— это число запросов в системе в момент t, а 
— время отклика n-го запроса.
Теорема была формально доказана только в 1961 г., хотя само соотношение было известно задолго до этого.
На самом деле, если внутри системы запросы могут переупорядочиться, то всё немного сложнее, поэтому будем для простоты считать, что этого не происходит. Хотя теорема верна и в этом случае тоже. Теперь подсчитаем площадь между графиками. Это можно сделать двумя способами. Во-первых, по колонкам — как обычно считают интегралы. В этом случае получается, что подынтегральное выражение — это размер очереди в штуках. Во-вторых, построчно — просто сложив latency всех запросов. Понятно, что оба вычисления дают одну и ту же площадь, поэтому равны. Если обе части этого равенства поделить на время Δt, за которое мы считали площадь, то слева у нас будет средняя длина очереди (по определению среднего). Справа немного сложнее. Нужно в числитель и знаменатель вставить ещё число запросов N, тогда у нас получится
Важно сказать, что в доказательстве мы не использовали никакие распределения никаких вероятностей. По сути, теорема Литтла — это детерминистический закон! Такие законы называются в теории массового обслуживания operational law. Их можно применять к любым частям системы и любым распределениям всевозможных случайных величин. Эти законы образуют конструктор, который можно успешно использовать для анализа средних значений в сетях. Недостаток в том, что все они применимы только к средним величинам и не дают никакого знания о распределениях.
Возвращаясь к вопросу, почему нельзя применять теорему Литтла к байтам, предположим, что и теперь измеряются не в штуках, а в байтах. Тогда, проводя аналогичное рассуждение, мы получим вместо странную вещь — площадь, деленную на общее число байт. Это по-прежнему секунды, но это что-то вроде средневзвешенного latency, где запросы большего размера получают больший вес. Можно эту величину назвать средней латентностью байта — что, в общем, логично, поскольку мы заменили штуки на байты — но никак не латентностью запроса.
Теорема Литтла говорит, что при определенном потоке запросов время отклика и число запросов в системе пропорциональны. Если все запросы выглядят одинаково, то среднее время отклика нельзя уменьшить, не наращивая мощности. Если же мы знаем размеры запросов заранее, можно пытаться переупорядочить их внутри, чтобы уменьшить площадь между и и, следовательно, среднее время отклика системы. Продолжая эту мысль, можно доказать, что алгоритмы Shortest Processing Time и Shortest Remaining Processing Time дают для одного сервера минимальное среднее время отклика без возможности вытеснения и с ней соответственно. Но есть побочный эффект — большие запросы могут не обрабатываться бесконечно долго. Феномен называется «голодание» (starvation) и тесно связан с понятием справедливости планирования, о котором можно узнать из предыдущего поста Scheduling: мифы и реальность.
Есть ещё одна распространённая ловушка, связанная с пониманием закона Литтла. Имеется однопоточный сервер, который обслуживает запросы пользователей. Допустим, мы как-то измерили L — среднее число запросов в очереди к этому серверу, и S — среднее время обслуживания одного запроса сервером. Теперь рассмотрим новый входящий запрос. В среднем он видит впереди себя L запросов. На обслуживание каждого из них уходит в среднем S секунд. Получается, что среднее время ожидания
. Но по теореме получается, что 
. Если приравнять выражения, то увидим нонсенс: 
. Что не так в этом рассуждении?
Итак, теорему Литтла можно применять к большим и маленьким системам, к очередям, к серверам и к одиночным потокам обработки. Но во всех этих случаях обычно запросы тем или иным образом классифицируются. Запросы разных пользователей, запросы разного приоритета, запросы, приходящие из разных локаций, или запросы разного типа. В этом случае агрегированная по классам информация не интересна. Да, среднее число перемешанных запросов и среднее время отклика по всем ним опять пропорциональны. Но как быть, если мы хотим узнать среднее время отклика для определенного класса запросов? Удивительно, но теорему Литтла можно применять и для конкретного класса запросов. В этом случае нужно взять в качестве скорость поступления запросов этого класса, а не всех. В качестве и — средние значения числа и времени пребывания запросов этого класса в исследуемой части системы.
Стоит отметить, что для закрытых систем «неверный» ход рассуждений, приводящий к выводу оказывается верным. Закрытые системы — это такие системы, в которые запросы не приходят извне и не уходят наружу, а циркулируют внутри. Или, иначе, системы с обратной связью: как только запрос покидает систему, новый запрос занимает его место. Эти системы важны ещё и потому, что любую открытую систему можно рассматривать как погружённую в закрытую систему. Например, можно рассматривать сайт как открытую систему, в которую постоянно сыпятся запросы, обрабатываются и уходят, а можно, наоборот, как закрытую систему вместе со всей аудиторией сайта. Тогда обычно говорят, что число пользователей фиксировано, и они либо ждут ответа на запрос, либо «думают»: получили свою страницу и пока не кликнули по ссылке. В том случае, если think time всегда нулевой, систему ещё называют батч-системой.
Закон Литтла для закрытых систем справедлив, если скорость внешних прибытий (их нет в закрытой системе) заменить на пропускную способность системы. Если завернуть однопоточный сервер, рассмотренный выше, в батч-систему, мы получим и утилизацию 100%. Часто такой взгляд на систему даёт неожиданные результаты. В 90-х годах именно такое рассмотрение интернета вместе с пользователями как единой системы дало толчок к изучению распределений, отличных от экспоненциальных. Распределения мы обсудим дальше, а здесь отметим, что в то время практически всё и везде рассматривалось как экспоненциальное, и этому даже находили какое-то обоснование, а не просто оправдание в духе «иначе слишком сложно». Однако оказалось, что не все практически важные распределения имеют одинаково длинные хвосты, и знание о хвостах распределения можно пытаться использовать. Но пока вернёмся к средним величинам.
Предположим, у нас имеется открытая система: сложная сеть или простой однопоточный сервер — не важно. Что изменится, если ускорить вдвое поступление запросов и ускорить вдвое их обработку — например, увеличив мощность всех компонент системы в два раза? Как поменяются утилизация, пропускная способность, среднее число запросов в системе и среднее время ответа? Для однопоточного сервера можно попытаться взять формулы, применить их «в лоб» и получить результаты, но что делать с произвольной сетью? Интуитивное решение следующее. Предположим, что время ускорилось в два раза, тогда в нашей «ускоренной системе отсчёта» скорость серверов и поток запросов как будто не менялись; соответственно, все параметры в ускоренном времени имеют те же значения, что и раньше. Иными словами, ускорение всех «движущихся частей» любой системы эквивалентно ускорению часов. Теперь преобразуем значения в систему с нормальным временем. Безразмерные величины (утилизация и среднее число запросов) не поменяются. Величины, размерность которых включает временные множители первой степени, изменятся пропорционально. Пропускная способность [запросов / с] увеличится вдвое, а время отклика и ожидания [с] уменьшится вдвое.
Этот результат можно интерпретировать двумя способами:
Ещё раз замечу, что это верно для широкого класса систем, а не только для простого сервера. С практической точки зрения есть только две проблемы:
Рассмотрим предельный переход. Предположим, в этой же открытой системе интерпретацию № 2. Мы делим каждый входящий запрос пополам. Время отклика тоже делится пополам. Повторяем деление много раз. Причём нам даже не надо ничего менять в системе. Получается, можно сделать время отклика сколь угодно малым, просто распиливая входящие запросы на достаточно большое число частей. В пределе можно сказать, что у нас вместо запросов получается «запросная жидкость», которую мы фильтруем нашими серверами. Это так называемая fluid model, очень удобный инструмент для упрощённого анализа. Но почему время отклика равно нулю? Что пошло не так? В каком месте мы не учли латентность? Оказывается, мы не учли как раз скорость света, её нельзя удвоить. Время распространения в сетевом канале нельзя поменять, с ним можно только смириться. Фактически передача через сеть включает две компоненты: время передачи (transmission time) и время распространения (propagation time). Первое можно ускорить, наращивая мощность (ширину канала) или уменьшая размеры пакетов, а на второе очень сложно повлиять. В нашей «жидкостной модели» как раз отсутствовали какие-либо резервуары для накопления жидкостей — сетевые каналы с ненулевым и постоянным временем распространения. Кстати, если их добавить в нашу «жидкостную модель», латентность будет определяться суммой времён распространения, а очереди в узлах будут по-прежнему пусты. Очереди зависят только от размеров пакетов и вариативности (читай burst) входного потока.
Из этого следует, что если речь идёт про латентность, нельзя обойтись расчётами потоков, и даже утилизация устройств всего не решает. Нужно обязательно учитывать размеры запросов и не забывать про время распространения, которое часто игнорируют в теории массового обслуживания, хотя добавить его в расчёты совсем не сложно.
В чем вообще причина образования очередей? Очевидно, в системе недостаточно мощностей, и избыток запросов накапливается? Не верно! Очереди возникают также в системах, где ресурсов достаточно. Если мощностей недостаточно, то система, как говорят теоретики, не стабильна. Есть две основные причины образования очередей: нерегулярность поступления запросов и вариативность размеров запросов. Мы уже рассматривали пример, в котором обе эти причины были устранены: система реального времени, где запросы одинакового размера приходят строго периодически. Очередь никогда не образуется. Среднее время ожидания в очереди равно нулю. Понятно, что добиться такого поведения очень сложно, если не невозможно, поэтому и образуются очереди. Теория массового обслуживания исходит из предположения, что обе причины носят случайный характер и описываются некоторыми случайными величинами.
Для описания разных систем используется нотация Кендалла A/S/k/K, где A — распределение времени между запросами, S — распределение размеров запросов, k — число серверов, K — ограничение на одновременное число запросов в системе (опускается, если ограничения нет). Например, широко известная M/M/1 расшифровывается так: первая M (Markovian или Memoryless) обозначает, что на вход в систему подаётся пуассоновский поток задач. Читай: сообщения приходят в случайные моменты времени с заданной средней скоростью запросов в секунду — прямо как при радиоактивном распаде — или, более формально: время между двумя соседними событиями имеет экспоненциальное распределение. Вторая M обозначает, что обслуживание этих сообщений тоже имеет экспоненциальное распределение и в среднем обрабатывается μ запросов в секунду. И наконец, единица в конце обозначает, что обслуживание выполняется одним сервером. Очередь не ограничена, так как 4-я часть нотации отсутствует. Буквы, которые используются в этой нотации, довольно странно выбраны: G — произвольное распределение (нет, не гауссово, как можно было бы подумать), D — deterministic. Cистема реального времени — D/D/1. Первая система теории массового обслуживания, которую решил Эрланг в 1909 г., — M/D/1. А вот нерешённая пока аналитически система — M/G/k для k>1, причём решение для M/G/1 нашли ещё в 1930-м.
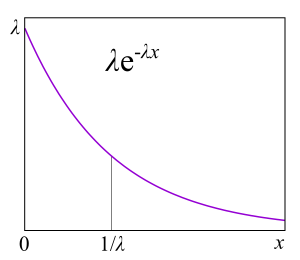Основная причина в том, что они делают почти любую задачу про очереди решаемой, поскольку, как мы увидим дальше, появляется возможность применять цепи Маркова, про которые математики уже много всего знают. Экспоненциальные распределения имеют много хороших для теории свойств, потому что они не обладают памятью. Я не стану приводить здесь определение этого свойства, для разработчиков будет более полезным объяснение через failure rate. Предположим, у вас есть некое устройство, а из практики вы знаете распределение времени жизни таких устройств: они часто выходят из строя в начале жизни, затем ломаются относительно редко и после истечения гарантийного срока опять начинают часто ломаться. Формально эта информация как раз и содержится в failure rate function, которая довольно просто связана с распределением. По сути, это «выровненная» плотность вероятности с учётом того, что устройство дожило до некоторого момента. С практической точки зрения это именно то, что нам интересно: частота отказов устройств как функция времени, которое они уже находятся в эксплуатации. Например, если failure rate — константа, то есть частота отказа устройства не зависит от времени эксплуатации, а отказы просто происходят случайно с какой-то частотой, тогда распределение времени жизни устройства — экспоненциальное. В этом случае, чтобы предсказать, сколько устройство проработает, не надо знать, как долго оно находится в эксплуатации, какой у него износ и что бы то ни было другое. Это и есть «отсутствие памяти».
Failure rate можно вычислить для любого распределения. В теории массового обслуживания — для распределения времени выполнения запроса. Failure rate говорит, как долго ещё запрос будет выполняться, исходя из того, сколько он уже выполняется. Если у нас возрастающий failure rate, то чем дольше запрос выполняется, тем больше вероятность, что он скоро закончится. Если у нас убывающий failure rate, то чем дольше запрос выполняется, тем больше вероятность, что он будет выполняться еще дольше. Как вам кажется, какой из этих двух вариантов наиболее типичен для вычислительных систем, баз данных и прочего, связанного с software и hardware? Для начала: почему это вообще важно? Пример из повседневной жизни. Вы стоите в очереди в кассу, поначалу очередь продвигается хорошо, но в какой-то момент перестаёт двигаться. Стоит ли перейти в другую очередь такой же длины? Если обслуживание имеет экспоненциальное распределение, то ответ — без разницы. В случае распределения с тяжёлым хвостом (убывающий failure rate) может быть выгодно мигрировать в другую очередь. Такого рода «анализ ситуации» можно применять для балансировки или миграции процессов.
Выясняется, что на производстве чаще встречаются распределения или экспоненциальные, или с возрастающим failure rate, а в компьютерных системах, наоборот, времена выполнения всяческих запросов или unix-процессов имеют распределения с тяжёлым хвостом. Это довольно неожиданная новость, и я решил её проверить.
RTMR выполняет много разного прикладного кода над данными, которые создаются из сессий пользователей поиска. Я вооружился LWTrace и оттрассировал с нашего продакшен-кластера все нужные данные. Меня интересовало только время работы пользовательского кода. Стриминговая обработка происходит довольно быстро, поэтому мне не составило труда собрать данные о примерно миллионе случайно выбранных запусков на случайных машинах в течение нескольких часов. Поскольку меня интересовал хвост распределения, я построил график распределения
в двойных логарифмических осях. Чтобы понять, возрастающий или убывающий failure rate имеет это распределение, я сравнил его с двумя другими распределениями, которые имеют точно такое же среднее значение: экспоненциальным и распределением Парето.
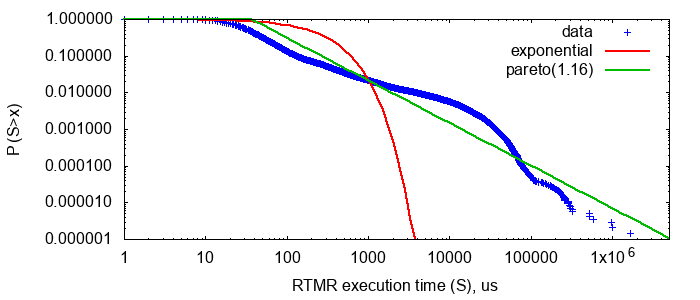
Распределение Парето имеет степенную форму
, и поэтому затухает медленнее любой экспоненты — имеет тяжёлый хвост. Ещё оно знаменито тем, что часто встречается в «дикой природе», принцип 80/20: распределение богатства в обществе, размеров файлов в интернете и т. п. В двойных логарифмических осях оно превращается в прямую, что очень удобно для сравнения на глаз. Как видите, в RTMR мы имеем что-то, больше похожее на Парето, чем на экспоненту. Параметр 
, что соответствует принципу 80/20: всего 20% запросов создают 80% нагрузки.
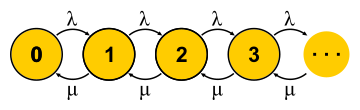Эту большую тему невозможно объять парой абзацев, но я постараюсь. Цепи Маркова позволяют взглянуть на конечный автомат с вероятностной точки зрения. Для этого предполагают, что события, которые меняют состояние автомата, случайны и автомат просто переходит между состояниями с какими-то известными вероятностями. Для теории массового обслуживания используют автомат, состояния которого — это число запросов в системе. Событие «новый запрос» переводит автомат в следующее состояние, а событие «завершение обслуживания» — обратно. Спрашивается: что будет, если предоставить такому автомату достаточно времени? Допустим, много таких автоматов существует параллельно (ансамбль автоматов, если угодно), и они независимо и случайно плавают из одного состояния в другое. Теперь рассмотрим некоторое состояние, например состояние 0 на рисунке. Чтобы число автоматов в этом состоянии оставалось неизменным, надо, чтобы скорость их поступления 
была уравновешена скоростью переходов в другие состояния 
. Таким образом, мы получим уравнений столько же, сколько и неизвестных — по числу состояний. Дальше решим систему и найдём так называемое равновесное распределение. Для каждого отдельного автомата это распределение говорит, какую долю времени в каком состоянии он пребывает. Недолгое жонглирование символами приводит для M/M/1 к результату 
, где 
— это утилизация сервера. Конец истории. По ходу изложения я пропустил приличное количество предположений и сделал пару подмен понятий, но суть, надеюсь, не пострадала.
Важно понимать, что такой подход работает, только если текущее состояние автомата полностью определяет его дальнейшее поведение, а история о том, как он попал в это состояние, не важна. Для повседневного понимания конечного автомата это само собой разумеется — ведь на то оно и состояние. А вот для стохастического процесса из этого следует, что все распределения должны быть экспоненциальными, поскольку только они не обладают памятью — имеют константный failure rate.
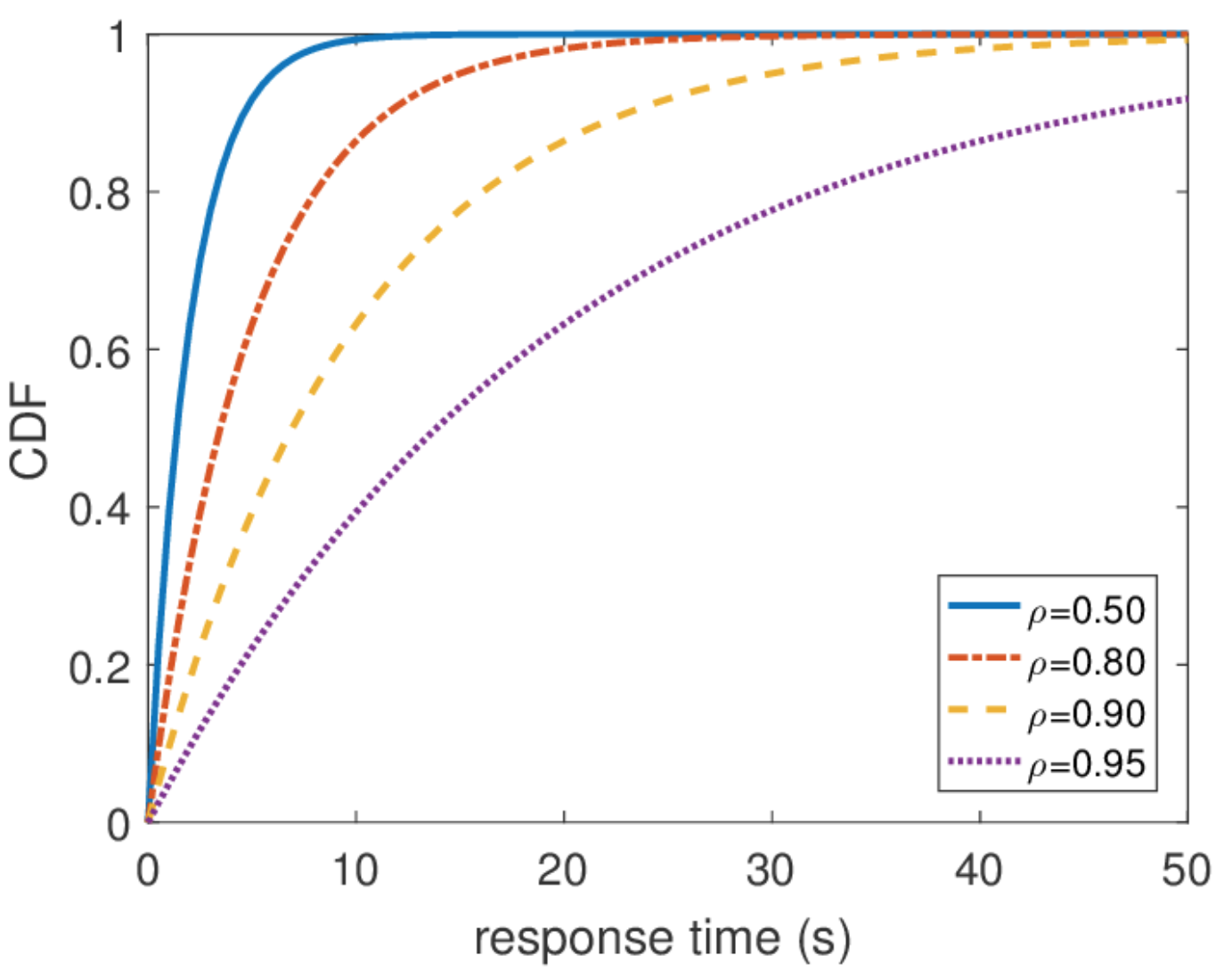Ещё важно сказать, что всю остальную информацию про систему легко получить, если мы знаем равновесное распределение. Среднее число запросов в системе — среднее значение этого распределения. Чтобы узнать среднее время отклика, применим теорему Литтла к числу запросов. Распределение времени отклика найти чуть сложнее, но тоже за несколько действий можно выяснить, что 
и что среднее время отклика 
.
По этому распределению можно найти любой перцентиль времени отклика, и оказывается, что сотый перцентиль равен бесконечности. Другими словами, худшее время отклика не ограничено сверху. Что, в общем-то, не удивительно, поскольку мы использовали пуассоновский поток. Но на практике такое поведение никогда не может встретиться. Очевидно, что входной поток запросов к серверу ограничен, хотя бы шириной сетевого канала к этому серверу, а длина очереди — памятью на этом сервере. Пуассоновский поток, напротив, с ненулевой вероятностью гарантирует возникновение сколь угодно больших бёрстов. Поэтому я бы не рекомендовал при проектировании системы исходить из предположения пуассоновского входного потока, если вас интересуют высокие перцентили, а загрузка системы очень высока. Лучше использовать другие модели трафика, про которые я расскажу в другой раз, когда буду говорить о сетевом исчислении.
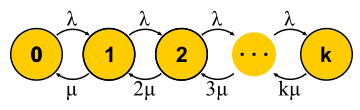Теперь, когда в нашем распоряжении есть достаточно мощный способ анализа систем, можно пытаться применять его к разным задачам и пожинать плоды. Примерно так развивалась теория массового обслуживания во второй половине ХХ века. Попробуем понять, чего удалось добиться. Для начала вернёмся к задачам, которые решал Эрланг. Это задачи M/M/k/k и M/M/k, в которых нам бы хотелось ограничивать вероятность отказа. Оказывается, для них несложно построить цепи Маркова. Отличие в том, что по мере прибавления задач вероятность обратного перехода увеличивается, так как задачи начинают обрабатываться параллельно, но когда число задач становится равно числу серверов, происходит насыщение. Дальше для M/M/k/k сеть заканчивается, автомат действительно оказывается конечным, и все запросы, которые приходят в последнее состояние, получают отказ. Вероятность этого события просто равна вероятности того, что мы находимся в последнем состоянии.
Для M/M/k дело обстоит сложнее, запросы встают в очередь, появляются новые состояния, но вероятность обратного перехода не увеличивается — уже все серверы работают. Сеть становится бесконечной, как для M/M/1. Кстати, если число запросов в системе ограничено, то цепь всегда будет иметь конечное число состояний и так или иначе будет решаться, чего не скажешь про бесконечные цепи. В закрытых системах цепи всегда конечны. Решая описанные цепи для M/M/k/k и M/M/k, мы придём к формуле B и формуле С Эрланга соответственно. Они довольно громоздкие, я не буду их приводить, но с их помощью можно получить интересный для развития интуиции результат, который называется square root staffing rule. Допустим, имеется система M/M/k с каким-то заданным входным потоком λ запросов в секунду. Предположим, что нагрузка должна завтра увеличиться в два раза. Спрашивается: как надо увеличить число серверов, чтобы время отклика осталось прежним? Число серверов надо удвоить, верно? Оказывается, вовсе нет. Вспомним, что мы уже видели: если ускорить время (серверы и вход) вдвое, то среднее время отклика уменьшается вдвое. Несколько медленных и один быстрый сервер — это не одно и то же, но тем не менее вычислительная мощность одинакова. В частности, для M/M/1 например, время отклика обратно пропорционально объёму «свободной ёмкости» 
и определяется только этим объёмом. При увеличении и потока, и вычислительной мощности вдвое, свободная ёмкость системы удваивается: 
. Может показаться, что для решения задачи нужно просто сохранить свободную ёмкость, но время отклика в M/M/k определяется уже по более сложной формуле Эрланга. Оказывается, что свободную ёмкость нужно поддерживать пропорционально квадратному корню из числа «занятых серверов», чтобы сохранить прежнее время отклика. Под числом «занятых серверов» подразумевается общее число серверов, умноженное на утилизацию: это минимально необходимое для стабильной работы число серверов.
Используя данное правило, иногда пытаются обосновать, как расширять кластер с серверами. Но не стоит питать иллюзий, что любой кластер — это M/M/k-система. Например, если у вас на входе используется балансер, который отправляет запросы в очереди на серверы, — это уже не M/M/k, так как M/M/k подразумевает общую очередь, из которой серверы забирают запросы, когда освобождаются. Зато эта модель подходит, например, для тредпулов с общей FIFO-очередью. Однако даже в этом случае стоит помнить, что это правило является аппроксимацией для случая, когда тредов много. По факту, если у вас больше 10 тредов, можно смело считать, что их много. Ну и не забываем про вездесущие экспоненциальные распределения: без предположения экспоненциальности всех распределений правило тоже не работает.
В конечном счёте, интерес представляет сеть из M/M/k, соединённых хотя бы в цепочку, так как мы делаем распределённые системы. Для изучения сетей хотелось бы иметь конструктор: простые и понятные правила соединения известных элементов в блоки. В теории управления, например, есть передаточные функции, которые понятным образом комбинируются при последовательных или параллельных соединениях. Здесь же выходной поток из любого узла имеет очень сложное распределение, за исключением M/M/k, которая по известной теореме Бёрка выдаёт независимый пуассоновский поток. Это исключение, как можно догадаться, в основном и используется.
Соединение двух пуассоновских потоков — пуассоновский поток. Вероятностное разделение пуассоновского потока на два — опять даёт два пуассоновских потока. Всё это приводит к тому, что все очереди в системе как бы независимы, и можно получить, выражаясь формальным языком, так называемое product-form solution. То есть совместное распределение длин очередей является просто произведением распределений длин всех очередей, рассматриваемых по отдельности — именно так в теории вероятностей выражается независимость. Просто находим входные потоки во все узлы и используем формулы для каждого узла независимо. Есть ряд ограничений:
Пример сети Джексона.
Стоит отметить, что при наличии обратной связи НЕ получается пуассоновский поток, так как потоки оказываются взаимозависимыми. На выходе из узла с обратной связью тоже получается непуассоновский поток, и в итоге все потоки становятся непуассоновскими. Однако удивительным образом оказывается, что все эти непуассоновские потоки ведут себя ровно так же, как пуассоновские (ох уж эта теория вероятностей), если выполняются указанные выше ограничения. И тогда мы опять получаем product-form solution. Такие сети имеют название Jackson networks, в них возможны обратные связи и, следовательно, множественные посещения любого сервера. Есть и другие сети, в которых позволяется больше вольностей, но в результате все значимые аналитические достижения теории массового обслуживания по отношению к сетям предполагают пуассоновские потоки на входе и product-form solution, что стало предметом критики этой теории и привело в 90-х как к разработке других теорий, так и к изучению того, какие на самом деле распределения нужны и как с ними работать.
Важное применение всей этой теории сетей Джексона — моделирование пакетов в IP-сетях и ATM-сетях. Модель достаточно адекватна: размеры пакетов не сильно меняются и не зависят от самого пакета, только от ширины канала, так как время обслуживания соответствует времени передачи пакета в канал. Случайное время отправки, хоть и звучит дико, на самом деле обладает не очень большой вариативностью. Более того, оказывается, что в сети с детерминированным временем обслуживания латентность не может быть больше, чем в аналогичной сети Джексона, поэтому такие сети смело можно использовать для оценки времени отклика сверху.
Все результаты, о которых я рассказал, относились к экспоненциальным распределениям, но я также упомянул, что реальные распределения отличаются. Возникает ощущение, что вся эта теория достаточно бесполезна. Это не совсем так. Есть способ встроить в этот математический аппарат и другие распределения, более того, практически любые распределения, но это будет кое-чего нам стоить. За исключением нескольких интересных случаев, теряется возможность получить решение в явном виде, теряется product-form solution, а вместе с ним конструктор: каждую задачу нужно решать целиком с нуля, используя цепи Маркова. Для теории это большая проблема, но на практике это просто означает применение численных методов и даёт возможность решать куда более сложные и приближенные к реальности задачи.
Идея проста. Цепи Маркова не позволяют нам иметь память внутри одного состояния, поэтому все переходы должны быть случайными с экспоненциальным распределением времени между двумя преходами. Но что если состояние разбить на несколько подсостояний? Переходы между подсостояниями по-прежнему должны иметь экспоненциальное распределение, если мы хотим, чтобы вся конструкция оставалась цепью Маркова, а мы этого очень хотим, поскольку знаем, как решать такие цепи. Подсостояния часто называют фазами, если они выстроены последовательно, а процесс разбиения — методом фаз.
Самый простой пример. Обработка запроса выполняется в несколько фаз: сначала мы, например, читаем нужные данные из базы, затем выполняем какие-нибудь вычисления, потом записываем результаты в базу. Допустим, все эти три стадии имеют одинаковое экспоненциальное распределение времени. Какое распределение имеет время прохождения всех трёх фаз вместе? Это распределение Эрланга.
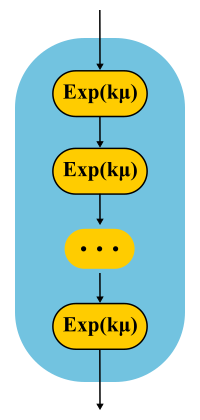
А что если сделать много-много коротких одинаковых фаз? В пределе получим детерминированное распределение. То есть, выстраивая цепочку, можно уменьшать вариативность распределения.
Можно ли увеличить вариативность? Легко. Вместо цепочки фаз используем альтернативные категории, случайно выбирая одну из них. Пример. Почти все запросы выполняются быстро, но есть небольшая вероятность, что придёт огромный запрос, который выполняется долго. Такое распределение будет иметь убывающий failure rate. Чем дольше мы ждём, тем больше вероятность, что запрос попал во вторую категорию.
Продолжая развивать метод фаз, теоретики выяснили, что есть класс распределений, с помощью которых можно приблизиться с любой точностью к произвольному неотрицательному распределению! Coxian distibution строится методом фаз, только мы не обязаны проходить все фазы, после каждой фазы есть некоторая вероятность завершения.
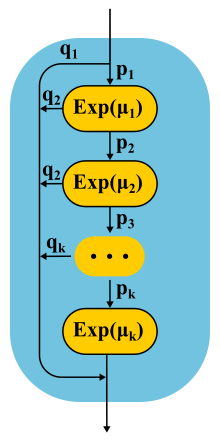
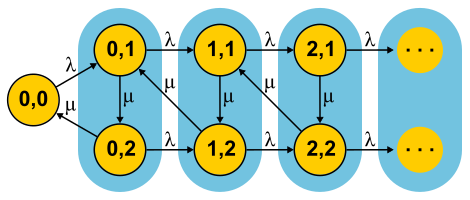
Такого рода распределения можно использовать как для генерации непуассоновского входного потока, так и для создания неэкспоненциального времени обслуживания. Вот, например, цепь Маркова для системы M/E2/1 с распределением Эрланга для времени обслуживания. Состояние определяется парой чисел (n, s), где n — длина очереди, а s — номер стадии, в которой находится сервер: первая или вторая. Возможны все комбинации n и s. Входящие сообщения меняют только n, а по завершении фаз происходит их чередование и уменьшение длины очереди после завершения второй фазы.
Может ли тормозить система, загруженная вполовину своей мощности? В качестве первого подопытного препарируем M/G/1. Дано: пуассоновский поток на входе и произвольное распределение времени обслуживания. Рассмотрим путь одного запроса через всю систему. Случайно поступающий входящий запрос видит в очереди перед собой среднее по времени число запросов![$\mathbf{E}[N_Q]$](https://habrastorage.org/getpro/habr/formulas/2b3/15f/8f1/2b315f8f114054ebaab5c5555e670d3a.svg)
. Среднее время обработки каждого из них ![$\mathbf{E}[S]$](https://habrastorage.org/getpro/habr/formulas/9c5/9ef/289/9c59ef2892bff977cc035db99ceee803.svg)
. С вероятностью, равной утилизации 
, в сервере есть ещё один запрос, который нужно сначала «дообслужить» за время ![$\mathbf{E}[S_e]$](https://habrastorage.org/getpro/habr/formulas/2b8/cc6/71b/2b8cc671b30499feb76a0e79c39ca912.svg)
. Суммируя, получаем, что полное время ожидания в очереди ![$\mathbf{E}[T_Q] = \mathbf{E}[N_Q] \mathbf{E}[S] + \rho \mathbf{E}[S_e]$](https://habrastorage.org/getpro/habr/formulas/5b1/c31/1ca/5b1c311caad51431e9d4c3edfeefc5b4.svg)
. По теореме Литтла ![$\mathbf{E}[N_Q] = \lambda \mathbf{E}[T_Q]$](https://habrastorage.org/getpro/habr/formulas/c7d/43e/c3c/c7d43ec3c94792e84a5547f03ac2c2cc.svg)
; комбинируя, получаем: , видит, что на дообслуживание нужно время 
.
Среднее время определяется средним значением функции , то есть площадью треугольников, делённой на общее время. Понятно, что можно ограничиться одним «средним» треугольником, тогда ![$\mathbf{E}[S_e] = \mathbf{E}[S^2] / 2\mathbf{E}[S]$](https://habrastorage.org/getpro/habr/formulas/6af/f06/c3b/6aff06c3b5b8198ce7e3367620dbf899.svg)
. Это довольно неожиданно. Мы получили, что время дообслуживания определяется не только средним значением времени обслуживания, но и его вариативностью. Объяснение простое. Вероятность попасть в длинный интервал 
больше, она на самом деле пропорциональна длительности S этого интервала. Это объясняет знаменитый Waiting Time Paradox, или Inspection Paradox. Но вернёмся к M/G/1. Если скомбинировать всё, что мы получили, и переписать, используя вариативность ![$С^2_S = \mathbf{E}[S] / \mathbf{E}[S]^2$](https://habrastorage.org/getpro/habr/formulas/90e/7b9/d1c/90e7b9d1cee5e1caabeb5f0157accac7.svg)
, получим известную формулу Pollaczek-Khinchine: 
. Это, согласитесь, намного больше, чем 
для экспоненциального распределения. В среднем всё выполняется супер быстро: ![$\mathbf{E}[S] = 263.792 мкс$](https://habrastorage.org/getpro/habr/formulas/75c/8de/6d5/75c8de6d5ce163c6b3b8169d8fe9b416.svg)
. Теперь предположим, что RTMR моделируется системой M/G/1, и пусть система будет не сильно загружена, утилизация 
. Подставляя в формулу, получим ![$\mathbf{E}[T_Q] = 1 * (381+1)/2 * 263.792 мкс = 50 мс$](https://habrastorage.org/getpro/habr/formulas/eef/9ed/9ef/eef9ed9efd45544d7cc3067eb0fe67e6.svg)
. Из-за микробёрстов даже такая быстрая и недоутилизированная система может превратиться в среднем в отвратительную. За 50 мс можно 6 раз сходить на жёсткий диск или, если повезёт, даже в дата-центр на другом континенте! Кстати, для G/G/1 существует аппроксимация, которая учитывает вариативность поступающего трафика: она выглядит точно так же, только вместо 
в ней сумма обоих вариативностей 
. Для случая с несколькими серверами дела обстоят лучше, но эффект нескольких серверов влияет только на первый множитель. Эффект вариативности остаётся: ![$\mathbf{E}[T_Q]^{G/G/k} ≈ \mathbf{E}[T_Q]^{M/M/k} (C^2_S + C^2_A) / 2$](https://habrastorage.org/getpro/habr/formulas/cd7/c93/12f/cd7c9312ff51914db8e8bf0388053cfc.svg)
.
Как выглядят микробёрсты? Применительно к тредпулам это задачи, которые обслуживаются достаточно быстро, чтобы не быть заметными на графиках утилизации, и достаточно медленно, чтобы создать очередь за собой и влиять на время отклика пула. С точки зрения теории — это огромные запросы из хвостовой части распределения. Скажем, у вас пул из 10 тредов, и вы смотрите на график утилизации, построенный по метрикам времении работы и времени простоя, которые собираются раз в 15 секунд. Вы, во-первых, можете не заметить, что один тред вообще завис, или что все 10 тредов выполняли одновременно большие задачи целую секунду, а потом 14 секунд ничего не делали. Разрешающая способность в 15 секунд не позволяет увидеть скачок утилизации до 100% и обратно до 0%, а время отклика страдает. Например, так может выглядеть микробёрст, случающийся раз в 15 секунд в пуле из 6 потоков, если посмотреть на него через микроскоп.
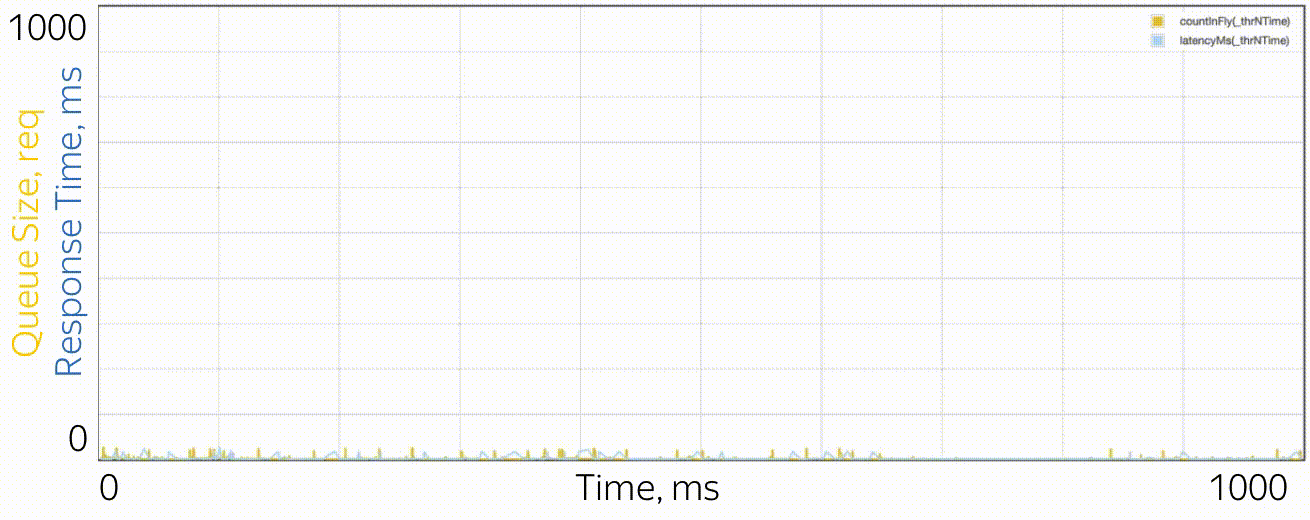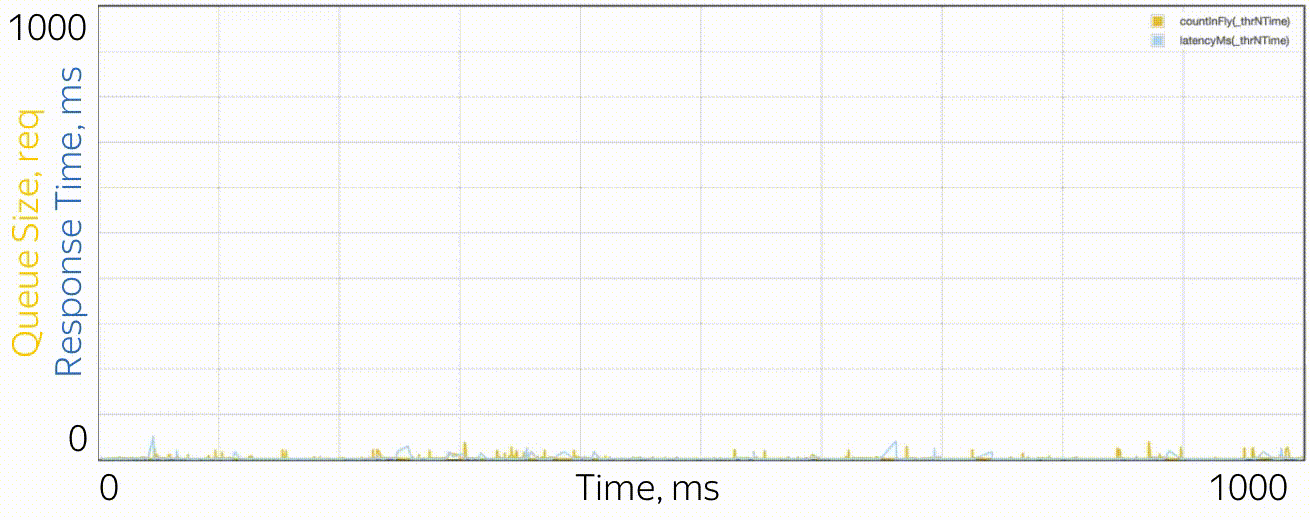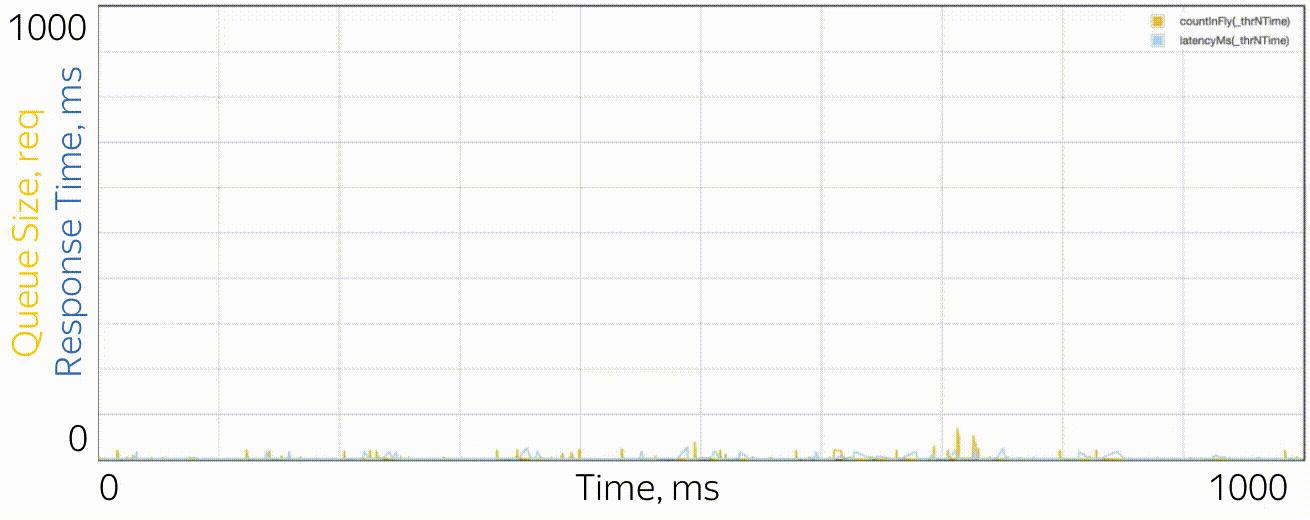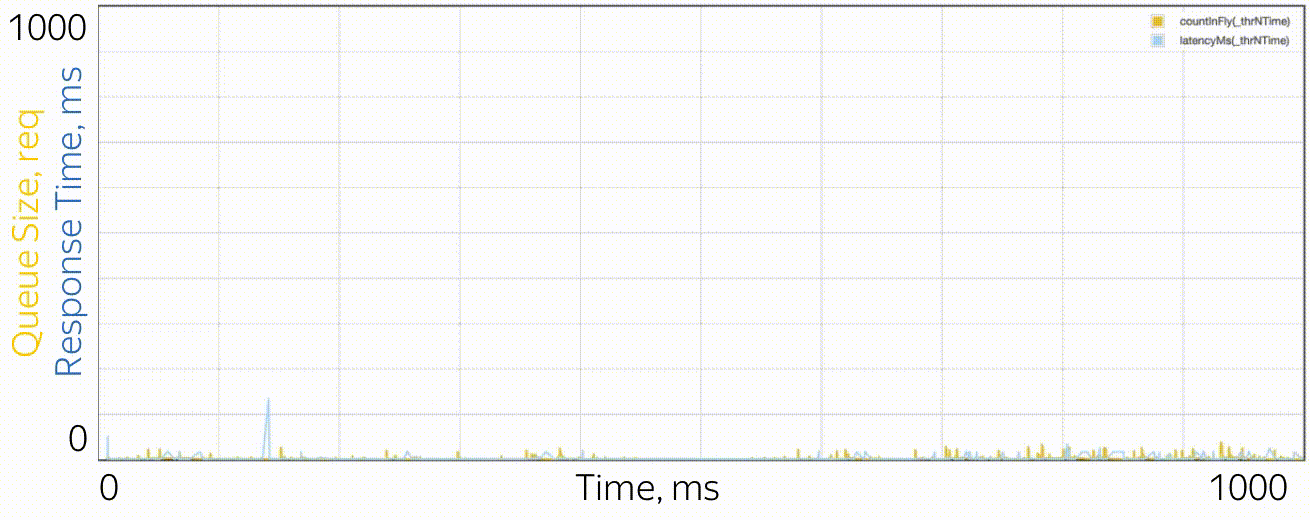
В качестве микроскопа используется система трассировки, регистрирующая время событий (поступление и завершение запросов) с точностью до циклов процессора.
Специально чтобы разбираться с подобными ситуациями, в RTMR используется механизм SelfPing, который строго периодически (каждые 10 мс), отправляет маленькую задачу в тредпул с единственной целью — замерить время ожидания в очереди. Предполагая худший случай, к этому замеру добавляется период 10 мс и берётся максимум на окне в 15 секунд. Таким образом, мы получаем оценку сверху на максимальное время ожидания на окне. Да, мы не видим реального положения дел, если время отклика меньше 10 мс, но в этом случае мы можем считать, что всё хорошо — нет ни единого микробёрста. Зато эта дополнительная self-ping-активность съедает строго ограниченное количество CPU. Механизм удобен тем, что он универсальный и неинвазивный: не нужно менять ни код тредпула, ни код задач, которые в нём выполняются. Подчеркну: измеряется именно худший случай, что очень удобно и интуитивно, по сравнению со всякими перцентилями. Также механизм обнаруживает и другую похожую ситуацию: одновременный приход большого количества вполне обычных запросов. Если их не настолько много, чтобы проблему было видно на 15-секундных графиках утилизации, — это тоже можно считать микробёрстом.
Хорошо, а как быть, если SelfPing показывает, что происходит нечто неадекватное? Как найти виновных? Для этого мы используем трассировку, уже упомянутый LWTrace. Идём на проблемную машину и через мониторинг запускаем трассировку, которая отслеживает в нужном тредпуле все задачи и сохраняет в памяти только медленные. Затем можно посмотреть топ-100 медленных трасс. После кратковременного исследования трассировку выключаем. Все другие способы поиска виновных не подходят: писать логи на все задачи тредпула невозможно; писать только медленные задачи — тоже не самое лучшее решение, так как всё равно придётся собирать трассу для всех задач, а это тоже накладно; профилирование с помощью perf не поможет, так как тяжёлые задачи случаются слишком редко, чтобы быть заметными в профиле.
У нас осталась ещё одна «степень свободы», которую мы до сих пор не использовали. Входящий поток и размеры запросов мы обсудили, разные количества серверов тоже, но ещё не говорили о планировщиках. Все примеры подразумевали FIFO-обработку. Как я уже упоминал, планирование действительно влияет на время отклика системы, и правильный планировщик может значительно улучшить latency (алгоритмы SPT и SRPT). Но планирование — это очень продвинутая тема для теории массового обслуживания. Возможно, эта теория даже не очень хорошо подходит для исследования планировщиков, но это единственная теория, которая может давать ответы про стохастические системы с планировщиками и позволяет вычислять средние значения. Есть другие теории, которые позволяют многое понять про планирование «в худшем случае», но про них мы поговорим в другой раз.
А сейчас рассмотрим несколько интересных исключений из общего правила, когда всё-таки удаётся получить product-form solution для сети и можно создать удобный конструктор. Начнём с одного узла M/Cox/1/PS. Пуассоновский поток на входе, практически произвольное распределение (Coxian distribution) времени обслуживания и справедливый планировщик (Processor Sharing), обслуживающий все запросы одновременно, но со скоростью, обратно пропорциональной их текущему числу. Где можно встретить такую систему? Например, именно так работают справедливые планировщики процессов в операционных системах. На первый взгляд может показаться, что это сложная система, но если построить (см. раздел метод фаз) и решить соответствующую цепь Маркова, то оказывается, что распределение длины очереди в точности повторяет систему M/M/1/FIFO, в которой время обслуживания имеет такое же среднее значение, но распределено экспоненциально.
Это невероятный результат! В противоположность тому, что мы видели в разделе про микробёрсты, здесь вариативность времени обслуживания никак не влияет на время отклика, ни в каком из перцентилей! Такое свойство редко встречается и называется insensitivity property. Обычно оно возникает в системах, где нет ожидания, и запрос сразу начинает так или иначе выполняться, когда не нужно дожидаться дообслуживания того, что уже выполняется. Другой пример системы с таким свойством — M/M/∞. В ней тоже нет ожидания, так как число серверов бесконечно. В таких системах выходной поток из узла имеет хорошее распределение, что позволяет получить product-form solution для сетей с такими серверами — сетей BCMP.
Для полноты картины рассмотрим простейший пример. Два сервера, работающие с разной средней скоростью (например, частота процессора отличается), произвольное распределение размеров поступающих задач, обслуживающий сервер выбирается случайно, бóльшая часть задач идёт на быстрый сервер. Нужно найти среднее время отклика. Решение. ![$\mathbf{E}[T] = 1/3 \mathbf{E}[T_1] + 2/3 \mathbf{E}[T_2]$](https://habrastorage.org/getpro/habr/formulas/9e8/a28/2e2/9e8a282e23452a27025daec9a7f77fa3.svg)
. Применим известную формулу ![$\mathbf{E}[T_i] = 1/(\mu_i - \lambda_i)$](https://habrastorage.org/getpro/habr/formulas/861/21d/7e5/86121d7e5dfa192b2aac9f1b71608b5f.svg)
для среднего времени отклика M/M/1/FCFS и получим ![$\mathbf{E}[T] = 1/3 * 1/(3 - 3 * 1/3) + 2/3 * 1/(4 - 3*2/3) = 0.5 с$](https://habrastorage.org/getpro/habr/formulas/db3/f78/065/db3f78065b10a9e731f9e5750bde5de6.svg)
.
Ну всё, теперь и планирование обсудили, можно закругляться. В следующей статье я расскажу, как в системах реального времени подходят к вопросу латентности и какие концепции используются там.
Меня зовут Сергей Трифонов, я работаю в команде Real-Time Map Reduce в Яндексе. Мы разрабатываем платформу для обработки потока данных в реальном времени с секундным и субсекундным временем отклика. Платформа доступна для внутренних пользователей и позволяет им выполнять прикладной код над постоянно поступающими потоками данных. Я попытаюсь сделать краткий обзор основных концепций человечества на тему анализа latency за последние сто десять лет, и сейчас мы попробуем понять, что именно про latency можно узнать, применяя теорию массового обслуживания.
Феномен латентности начали систематически исследовать, насколько мне известно, в связи с появлением систем массового обслуживания — телефонных сетей связи. Теория массового обслуживания началась с работы А. К. Эрланга 1909 г., в которой он показал, что пуассоновское распределение применимо к случайному телефонному трафику. Эрланг разработал теорию, которая многие десятилетия использовалась для проектирования телефонных сетей. Теория позволяет определить вероятность отказа в обслуживании. Для телефонных сетей с коммутацией каналов отказ происходил, если все каналы заняты и звонок не может быть совершён. Вероятность этого события нужно было контролировать. Хотелось иметь гарантию, что, например, 95% всех звонков будут обслужены. Формулы Эрланга позволяют определить, сколько нужно серверов для выполнения этой гарантии, если известна длительность и число звонков. По сути, эта задача как раз про гарантии качества, и сегодня люди по-прежнему решают похожие задачи. Но системы стали гораздо сложнее. Основная проблема теории массового обслуживания в том, что в большинстве институтов её не преподают, и мало кто понимает вопрос за пределами обычной очереди M/M/1 (см. про нотацию ниже), зато хорошо известно, что жизнь намного сложнее этой системы. Поэтому я предлагаю, минуя M/M/1, перейти сразу к самому интересному.
Средние величины
Если не пытаться обрести полное знание о распределении вероятностей в системе, а сосредоточиться на более простых вопросах, можно получить интересные и полезные результаты. Самый известный из них — это, конечно, теорема Литтла. Она применима к системе с любым входным потоком, внутренним устройством любой сложности и произвольным планировщиком внутри. Единственное требование в том, что система должна быть стабильна: должны существовать средние значения времени отклика и длины очереди, тогда они связаны простым выражением
— среднее по времени число запросов в рассматриваемой части системы [шт.], — среднее время, за которое запросы проходят через данную часть системы [с], — скорость поступления запросов в систему [шт./с]. Сила теоремы в том, что её можно применять к любой части системы: очередь, исполнитель, очередь + исполнитель или сеть целиком. Часто этой теоремой пользуются примерно так: «К нам льётся поток 1Gbit/s, а среднее время отклика мы измерили, и оно составляет 10 мс, следовательно в полёте у нас в среднем 1.25 MB». Так вот, это вычисление не верно. Точнее, верно, только если все запросы имеют одинаковый размер в байтах. Теорема Литтла считает запросы в штуках, а не в байтах.Как пользоваться теоремой Литтла
В математике часто бывает нужно изучить доказательство, чтобы получить настоящий insight. Это как раз такой случай. Теорема Литтла настолько хороша, что я приведу здесь набросок доказательства. Входящий трафик описывается функцией — число запросов, которые вошли в систему к моменту времени . Аналогично — число запросов, которые вышли из системы к моменту времени . Моментом входа (выхода) запроса считается момент получения (передачи) последнего его байта. Границы системы определяются лишь этими моментами времени, поэтому теорема получается широко применимой. Если нарисовать графики этих функций в одних осях, то легко увидеть, что — это число запросов в системе в момент t, а — время отклика n-го запроса.Теорема была формально доказана только в 1961 г., хотя само соотношение было известно задолго до этого.
На самом деле, если внутри системы запросы могут переупорядочиться, то всё немного сложнее, поэтому будем для простоты считать, что этого не происходит. Хотя теорема верна и в этом случае тоже. Теперь подсчитаем площадь между графиками. Это можно сделать двумя способами. Во-первых, по колонкам — как обычно считают интегралы. В этом случае получается, что подынтегральное выражение — это размер очереди в штуках. Во-вторых, построчно — просто сложив latency всех запросов. Понятно, что оба вычисления дают одну и ту же площадь, поэтому равны. Если обе части этого равенства поделить на время Δt, за которое мы считали площадь, то слева у нас будет средняя длина очереди
(по определению среднего). Справа немного сложнее. Нужно в числитель и знаменатель вставить ещё число запросов N, тогда у нас получится 
Важно сказать, что в доказательстве мы не использовали никакие распределения никаких вероятностей. По сути, теорема Литтла — это детерминистический закон! Такие законы называются в теории массового обслуживания operational law. Их можно применять к любым частям системы и любым распределениям всевозможных случайных величин. Эти законы образуют конструктор, который можно успешно использовать для анализа средних значений в сетях. Недостаток в том, что все они применимы только к средним величинам и не дают никакого знания о распределениях.
Возвращаясь к вопросу, почему нельзя применять теорему Литтла к байтам, предположим, что
и теперь измеряются не в штуках, а в байтах. Тогда, проводя аналогичное рассуждение, мы получим вместо странную вещь — площадь, деленную на общее число байт. Это по-прежнему секунды, но это что-то вроде средневзвешенного latency, где запросы большего размера получают больший вес. Можно эту величину назвать средней латентностью байта — что, в общем, логично, поскольку мы заменили штуки на байты — но никак не латентностью запроса.Теорема Литтла говорит, что при определенном потоке запросов время отклика и число запросов в системе пропорциональны. Если все запросы выглядят одинаково, то среднее время отклика нельзя уменьшить, не наращивая мощности. Если же мы знаем размеры запросов заранее, можно пытаться переупорядочить их внутри, чтобы уменьшить площадь между
и и, следовательно, среднее время отклика системы. Продолжая эту мысль, можно доказать, что алгоритмы Shortest Processing Time и Shortest Remaining Processing Time дают для одного сервера минимальное среднее время отклика без возможности вытеснения и с ней соответственно. Но есть побочный эффект — большие запросы могут не обрабатываться бесконечно долго. Феномен называется «голодание» (starvation) и тесно связан с понятием справедливости планирования, о котором можно узнать из предыдущего поста Scheduling: мифы и реальность.Есть ещё одна распространённая ловушка, связанная с пониманием закона Литтла. Имеется однопоточный сервер, который обслуживает запросы пользователей. Допустим, мы как-то измерили L — среднее число запросов в очереди к этому серверу, и S — среднее время обслуживания одного запроса сервером. Теперь рассмотрим новый входящий запрос. В среднем он видит впереди себя L запросов. На обслуживание каждого из них уходит в среднем S секунд. Получается, что среднее время ожидания
. Но по теореме получается, что . Если приравнять выражения, то увидим нонсенс: . Что не так в этом рассуждении?- Первое, что бросается в глаза: время отклика по теореме не зависит от S. На самом деле, кончено же, зависит. Просто средняя длина очереди уже учитывает это: чем быстрее сервер — тем длина очереди короче и тем меньше время отклика.
- Мы рассматриваем систему, в которой очереди не копятся вечно, а регулярно обнуляются. Это значит, что утилизация сервера меньше 100% и мы пропускаем все входящие запросы, причем с той же средней скоростью, с которой эти запросы приходили, а значит в среднем обработка одного запроса занимает не S секунд, а больше —
секунд, просто потому, что иногда мы не обрабатываем никакие запросы. Дело в том, что в любой стабильной открытой системе без потерь пропускная способность не зависит от скорости серверов, она определяется только входным потоком. - Предположение о том, что входящий запрос видит в системе среднее по времени число запросов, не всегда верно. Контрпример: входящие запросы приходят строго периодически, и каждый запрос мы успеваем обработать до прихода следующего. Типичная картина для систем реального времени. Входящий запрос всегда видит в системе нуль запросов, но в среднем в системе, очевидно, больше нуля запросов. Если же запросы приходят в совершенно случайные моменты времени, то они действительно «видят среднее число запросов».
- Мы не учли, что с некоторой вероятностью в сервере уже может быть один запрос, который нужно «дообслужить». В общем случае, среднее время «дообслуживания» отличается от изначального времени обслуживания, и иногда, как ни парадоксально, может оказаться значительно больше. К этому вопросу мы вернёмся в конце, когда будем обсуждать микробёрсты, stay tuned.
Итак, теорему Литтла можно применять к большим и маленьким системам, к очередям, к серверам и к одиночным потокам обработки. Но во всех этих случаях обычно запросы тем или иным образом классифицируются. Запросы разных пользователей, запросы разного приоритета, запросы, приходящие из разных локаций, или запросы разного типа. В этом случае агрегированная по классам информация не интересна. Да, среднее число перемешанных запросов и среднее время отклика по всем ним опять пропорциональны. Но как быть, если мы хотим узнать среднее время отклика для определенного класса запросов? Удивительно, но теорему Литтла можно применять и для конкретного класса запросов. В этом случае нужно взять в качестве
скорость поступления запросов этого класса, а не всех. В качестве и — средние значения числа и времени пребывания запросов этого класса в исследуемой части системы.Открытые и закрытые системы
Стоит отметить, что для закрытых систем «неверный» ход рассуждений, приводящий к выводу оказывается верным. Закрытые системы — это такие системы, в которые запросы не приходят извне и не уходят наружу, а циркулируют внутри. Или, иначе, системы с обратной связью: как только запрос покидает систему, новый запрос занимает его место. Эти системы важны ещё и потому, что любую открытую систему можно рассматривать как погружённую в закрытую систему. Например, можно рассматривать сайт как открытую систему, в которую постоянно сыпятся запросы, обрабатываются и уходят, а можно, наоборот, как закрытую систему вместе со всей аудиторией сайта. Тогда обычно говорят, что число пользователей фиксировано, и они либо ждут ответа на запрос, либо «думают»: получили свою страницу и пока не кликнули по ссылке. В том случае, если think time всегда нулевой, систему ещё называют батч-системой.Закон Литтла для закрытых систем справедлив, если скорость внешних прибытий
(их нет в закрытой системе) заменить на пропускную способность системы. Если завернуть однопоточный сервер, рассмотренный выше, в батч-систему, мы получим и утилизацию 100%. Часто такой взгляд на систему даёт неожиданные результаты. В 90-х годах именно такое рассмотрение интернета вместе с пользователями как единой системы дало толчок к изучению распределений, отличных от экспоненциальных. Распределения мы обсудим дальше, а здесь отметим, что в то время практически всё и везде рассматривалось как экспоненциальное, и этому даже находили какое-то обоснование, а не просто оправдание в духе «иначе слишком сложно». Однако оказалось, что не все практически важные распределения имеют одинаково длинные хвосты, и знание о хвостах распределения можно пытаться использовать. Но пока вернёмся к средним величинам.Релятивистские эффекты
Предположим, у нас имеется открытая система: сложная сеть или простой однопоточный сервер — не важно. Что изменится, если ускорить вдвое поступление запросов и ускорить вдвое их обработку — например, увеличив мощность всех компонент системы в два раза? Как поменяются утилизация, пропускная способность, среднее число запросов в системе и среднее время ответа? Для однопоточного сервера можно попытаться взять формулы, применить их «в лоб» и получить результаты, но что делать с произвольной сетью? Интуитивное решение следующее. Предположим, что время ускорилось в два раза, тогда в нашей «ускоренной системе отсчёта» скорость серверов и поток запросов как будто не менялись; соответственно, все параметры в ускоренном времени имеют те же значения, что и раньше. Иными словами, ускорение всех «движущихся частей» любой системы эквивалентно ускорению часов. Теперь преобразуем значения в систему с нормальным временем. Безразмерные величины (утилизация и среднее число запросов) не поменяются. Величины, размерность которых включает временные множители первой степени, изменятся пропорционально. Пропускная способность [запросов / с] увеличится вдвое, а время отклика и ожидания [с] уменьшится вдвое.
Этот результат можно интерпретировать двумя способами:
- Ускоренная в k раз система может переварить поток задач в k раз больше, причём со средним временем отклика в k раз меньше.
- Можно сказать, что мощность не менялась, а просто размер задач уменьшился в k раз. Получается, что мы шлём в систему такую же нагрузку, но напиленную более мелкими кусочками. И… о чудо! Среднее время отклика уменьшается!
Ещё раз замечу, что это верно для широкого класса систем, а не только для простого сервера. С практической точки зрения есть только две проблемы:
- Не все части системы могут быть легко ускорены. На некоторые мы не можем никак повлиять вообще. Например, на скорость света.
- Не все задачи можно бесконечно делить на всё более мелкие, поскольку информацию не научились передавать порциями меньше одного бита.
Рассмотрим предельный переход. Предположим, в этой же открытой системе интерпретацию № 2. Мы делим каждый входящий запрос пополам. Время отклика тоже делится пополам. Повторяем деление много раз. Причём нам даже не надо ничего менять в системе. Получается, можно сделать время отклика сколь угодно малым, просто распиливая входящие запросы на достаточно большое число частей. В пределе можно сказать, что у нас вместо запросов получается «запросная жидкость», которую мы фильтруем нашими серверами. Это так называемая fluid model, очень удобный инструмент для упрощённого анализа. Но почему время отклика равно нулю? Что пошло не так? В каком месте мы не учли латентность? Оказывается, мы не учли как раз скорость света, её нельзя удвоить. Время распространения в сетевом канале нельзя поменять, с ним можно только смириться. Фактически передача через сеть включает две компоненты: время передачи (transmission time) и время распространения (propagation time). Первое можно ускорить, наращивая мощность (ширину канала) или уменьшая размеры пакетов, а на второе очень сложно повлиять. В нашей «жидкостной модели» как раз отсутствовали какие-либо резервуары для накопления жидкостей — сетевые каналы с ненулевым и постоянным временем распространения. Кстати, если их добавить в нашу «жидкостную модель», латентность будет определяться суммой времён распространения, а очереди в узлах будут по-прежнему пусты. Очереди зависят только от размеров пакетов и вариативности (читай burst) входного потока.
Из этого следует, что если речь идёт про латентность, нельзя обойтись расчётами потоков, и даже утилизация устройств всего не решает. Нужно обязательно учитывать размеры запросов и не забывать про время распространения, которое часто игнорируют в теории массового обслуживания, хотя добавить его в расчёты совсем не сложно.
Распределения
В чем вообще причина образования очередей? Очевидно, в системе недостаточно мощностей, и избыток запросов накапливается? Не верно! Очереди возникают также в системах, где ресурсов достаточно. Если мощностей недостаточно, то система, как говорят теоретики, не стабильна. Есть две основные причины образования очередей: нерегулярность поступления запросов и вариативность размеров запросов. Мы уже рассматривали пример, в котором обе эти причины были устранены: система реального времени, где запросы одинакового размера приходят строго периодически. Очередь никогда не образуется. Среднее время ожидания в очереди равно нулю. Понятно, что добиться такого поведения очень сложно, если не невозможно, поэтому и образуются очереди. Теория массового обслуживания исходит из предположения, что обе причины носят случайный характер и описываются некоторыми случайными величинами.
Для описания разных систем используется нотация Кендалла A/S/k/K, где A — распределение времени между запросами, S — распределение размеров запросов, k — число серверов, K — ограничение на одновременное число запросов в системе (опускается, если ограничения нет). Например, широко известная M/M/1 расшифровывается так: первая M (Markovian или Memoryless) обозначает, что на вход в систему подаётся пуассоновский поток задач. Читай: сообщения приходят в случайные моменты времени с заданной средней скоростью запросов в секунду — прямо как при радиоактивном распаде — или, более формально: время между двумя соседними событиями имеет экспоненциальное распределение. Вторая M обозначает, что обслуживание этих сообщений тоже имеет экспоненциальное распределение и в среднем обрабатывается μ запросов в секунду. И наконец, единица в конце обозначает, что обслуживание выполняется одним сервером. Очередь не ограничена, так как 4-я часть нотации отсутствует. Буквы, которые используются в этой нотации, довольно странно выбраны: G — произвольное распределение (нет, не гауссово, как можно было бы подумать), D — deterministic. Cистема реального времени — D/D/1. Первая система теории массового обслуживания, которую решил Эрланг в 1909 г., — M/D/1. А вот нерешённая пока аналитически система — M/G/k для k>1, причём решение для M/G/1 нашли ещё в 1930-м.Почему используют экспоненциальные распределения?
Основная причина в том, что они делают почти любую задачу про очереди решаемой, поскольку, как мы увидим дальше, появляется возможность применять цепи Маркова, про которые математики уже много всего знают. Экспоненциальные распределения имеют много хороших для теории свойств, потому что они не обладают памятью. Я не стану приводить здесь определение этого свойства, для разработчиков будет более полезным объяснение через failure rate. Предположим, у вас есть некое устройство, а из практики вы знаете распределение времени жизни таких устройств: они часто выходят из строя в начале жизни, затем ломаются относительно редко и после истечения гарантийного срока опять начинают часто ломаться. Формально эта информация как раз и содержится в failure rate function, которая довольно просто связана с распределением. По сути, это «выровненная» плотность вероятности с учётом того, что устройство дожило до некоторого момента. С практической точки зрения это именно то, что нам интересно: частота отказов устройств как функция времени, которое они уже находятся в эксплуатации. Например, если failure rate — константа, то есть частота отказа устройства не зависит от времени эксплуатации, а отказы просто происходят случайно с какой-то частотой, тогда распределение времени жизни устройства — экспоненциальное. В этом случае, чтобы предсказать, сколько устройство проработает, не надо знать, как долго оно находится в эксплуатации, какой у него износ и что бы то ни было другое. Это и есть «отсутствие памяти».Короткие и длинные хвосты
Failure rate можно вычислить для любого распределения. В теории массового обслуживания — для распределения времени выполнения запроса. Failure rate говорит, как долго ещё запрос будет выполняться, исходя из того, сколько он уже выполняется. Если у нас возрастающий failure rate, то чем дольше запрос выполняется, тем больше вероятность, что он скоро закончится. Если у нас убывающий failure rate, то чем дольше запрос выполняется, тем больше вероятность, что он будет выполняться еще дольше. Как вам кажется, какой из этих двух вариантов наиболее типичен для вычислительных систем, баз данных и прочего, связанного с software и hardware? Для начала: почему это вообще важно? Пример из повседневной жизни. Вы стоите в очереди в кассу, поначалу очередь продвигается хорошо, но в какой-то момент перестаёт двигаться. Стоит ли перейти в другую очередь такой же длины? Если обслуживание имеет экспоненциальное распределение, то ответ — без разницы. В случае распределения с тяжёлым хвостом (убывающий failure rate) может быть выгодно мигрировать в другую очередь. Такого рода «анализ ситуации» можно применять для балансировки или миграции процессов.
Выясняется, что на производстве чаще встречаются распределения или экспоненциальные, или с возрастающим failure rate, а в компьютерных системах, наоборот, времена выполнения всяческих запросов или unix-процессов имеют распределения с тяжёлым хвостом. Это довольно неожиданная новость, и я решил её проверить.
RTMR выполняет много разного прикладного кода над данными, которые создаются из сессий пользователей поиска. Я вооружился LWTrace и оттрассировал с нашего продакшен-кластера все нужные данные. Меня интересовало только время работы пользовательского кода. Стриминговая обработка происходит довольно быстро, поэтому мне не составило труда собрать данные о примерно миллионе случайно выбранных запусков на случайных машинах в течение нескольких часов. Поскольку меня интересовал хвост распределения, я построил график распределения
в двойных логарифмических осях. Чтобы понять, возрастающий или убывающий failure rate имеет это распределение, я сравнил его с двумя другими распределениями, которые имеют точно такое же среднее значение: экспоненциальным и распределением Парето.
Распределение Парето имеет степенную форму
, и поэтому затухает медленнее любой экспоненты — имеет тяжёлый хвост. Ещё оно знаменито тем, что часто встречается в «дикой природе», принцип 80/20: распределение богатства в обществе, размеров файлов в интернете и т. п. В двойных логарифмических осях оно превращается в прямую, что очень удобно для сравнения на глаз. Как видите, в RTMR мы имеем что-то, больше похожее на Парето, чем на экспоненту. Параметр , что соответствует принципу 80/20: всего 20% запросов создают 80% нагрузки.Цепи Маркова
Эту большую тему невозможно объять парой абзацев, но я постараюсь. Цепи Маркова позволяют взглянуть на конечный автомат с вероятностной точки зрения. Для этого предполагают, что события, которые меняют состояние автомата, случайны и автомат просто переходит между состояниями с какими-то известными вероятностями. Для теории массового обслуживания используют автомат, состояния которого — это число запросов в системе. Событие «новый запрос» переводит автомат в следующее состояние, а событие «завершение обслуживания» — обратно. Спрашивается: что будет, если предоставить такому автомату достаточно времени? Допустим, много таких автоматов существует параллельно (ансамбль автоматов, если угодно), и они независимо и случайно плавают из одного состояния в другое. Теперь рассмотрим некоторое состояние, например состояние 0 на рисунке. Чтобы число автоматов в этом состоянии оставалось неизменным, надо, чтобы скорость их поступления была уравновешена скоростью переходов в другие состояния . Таким образом, мы получим уравнений столько же, сколько и неизвестных — по числу состояний. Дальше решим систему и найдём так называемое равновесное распределение. Для каждого отдельного автомата это распределение говорит, какую долю времени в каком состоянии он пребывает. Недолгое жонглирование символами приводит для M/M/1 к результату , где — это утилизация сервера. Конец истории. По ходу изложения я пропустил приличное количество предположений и сделал пару подмен понятий, но суть, надеюсь, не пострадала.Важно понимать, что такой подход работает, только если текущее состояние автомата полностью определяет его дальнейшее поведение, а история о том, как он попал в это состояние, не важна. Для повседневного понимания конечного автомата это само собой разумеется — ведь на то оно и состояние. А вот для стохастического процесса из этого следует, что все распределения должны быть экспоненциальными, поскольку только они не обладают памятью — имеют константный failure rate.
Ещё важно сказать, что всю остальную информацию про систему легко получить, если мы знаем равновесное распределение. Среднее число запросов в системе — среднее значение этого распределения. Чтобы узнать среднее время отклика, применим теорему Литтла к числу запросов. Распределение времени отклика найти чуть сложнее, но тоже за несколько действий можно выяснить, что и что среднее время отклика .Неограниченное время отклика
По этому распределению можно найти любой перцентиль времени отклика, и оказывается, что сотый перцентиль равен бесконечности. Другими словами, худшее время отклика не ограничено сверху. Что, в общем-то, не удивительно, поскольку мы использовали пуассоновский поток. Но на практике такое поведение никогда не может встретиться. Очевидно, что входной поток запросов к серверу ограничен, хотя бы шириной сетевого канала к этому серверу, а длина очереди — памятью на этом сервере. Пуассоновский поток, напротив, с ненулевой вероятностью гарантирует возникновение сколь угодно больших бёрстов. Поэтому я бы не рекомендовал при проектировании системы исходить из предположения пуассоновского входного потока, если вас интересуют высокие перцентили, а загрузка системы очень высока. Лучше использовать другие модели трафика, про которые я расскажу в другой раз, когда буду говорить о сетевом исчислении.
Масштабирование и гарантии
Теперь, когда в нашем распоряжении есть достаточно мощный способ анализа систем, можно пытаться применять его к разным задачам и пожинать плоды. Примерно так развивалась теория массового обслуживания во второй половине ХХ века. Попробуем понять, чего удалось добиться. Для начала вернёмся к задачам, которые решал Эрланг. Это задачи M/M/k/k и M/M/k, в которых нам бы хотелось ограничивать вероятность отказа. Оказывается, для них несложно построить цепи Маркова. Отличие в том, что по мере прибавления задач вероятность обратного перехода увеличивается, так как задачи начинают обрабатываться параллельно, но когда число задач становится равно числу серверов, происходит насыщение. Дальше для M/M/k/k сеть заканчивается, автомат действительно оказывается конечным, и все запросы, которые приходят в последнее состояние, получают отказ. Вероятность этого события просто равна вероятности того, что мы находимся в последнем состоянии.
Для M/M/k дело обстоит сложнее, запросы встают в очередь, появляются новые состояния, но вероятность обратного перехода не увеличивается — уже все серверы работают. Сеть становится бесконечной, как для M/M/1. Кстати, если число запросов в системе ограничено, то цепь всегда будет иметь конечное число состояний и так или иначе будет решаться, чего не скажешь про бесконечные цепи. В закрытых системах цепи всегда конечны. Решая описанные цепи для M/M/k/k и M/M/k, мы придём к формуле B и формуле С Эрланга соответственно. Они довольно громоздкие, я не буду их приводить, но с их помощью можно получить интересный для развития интуиции результат, который называется square root staffing rule. Допустим, имеется система M/M/k с каким-то заданным входным потоком λ запросов в секунду. Предположим, что нагрузка должна завтра увеличиться в два раза. Спрашивается: как надо увеличить число серверов, чтобы время отклика осталось прежним? Число серверов надо удвоить, верно? Оказывается, вовсе нет. Вспомним, что мы уже видели: если ускорить время (серверы и вход) вдвое, то среднее время отклика уменьшается вдвое. Несколько медленных и один быстрый сервер — это не одно и то же, но тем не менее вычислительная мощность одинакова. В частности, для M/M/1 например, время отклика обратно пропорционально объёму «свободной ёмкости» и определяется только этим объёмом. При увеличении и потока, и вычислительной мощности вдвое, свободная ёмкость системы удваивается: . Может показаться, что для решения задачи нужно просто сохранить свободную ёмкость, но время отклика в M/M/k определяется уже по более сложной формуле Эрланга. Оказывается, что свободную ёмкость нужно поддерживать пропорционально квадратному корню из числа «занятых серверов», чтобы сохранить прежнее время отклика. Под числом «занятых серверов» подразумевается общее число серверов, умноженное на утилизацию: это минимально необходимое для стабильной работы число серверов.Используя данное правило, иногда пытаются обосновать, как расширять кластер с серверами. Но не стоит питать иллюзий, что любой кластер — это M/M/k-система. Например, если у вас на входе используется балансер, который отправляет запросы в очереди на серверы, — это уже не M/M/k, так как M/M/k подразумевает общую очередь, из которой серверы забирают запросы, когда освобождаются. Зато эта модель подходит, например, для тредпулов с общей FIFO-очередью. Однако даже в этом случае стоит помнить, что это правило является аппроксимацией для случая, когда тредов много. По факту, если у вас больше 10 тредов, можно смело считать, что их много. Ну и не забываем про вездесущие экспоненциальные распределения: без предположения экспоненциальности всех распределений правило тоже не работает.
Время отклика в сети
В конечном счёте, интерес представляет сеть из M/M/k, соединённых хотя бы в цепочку, так как мы делаем распределённые системы. Для изучения сетей хотелось бы иметь конструктор: простые и понятные правила соединения известных элементов в блоки. В теории управления, например, есть передаточные функции, которые понятным образом комбинируются при последовательных или параллельных соединениях. Здесь же выходной поток из любого узла имеет очень сложное распределение, за исключением M/M/k, которая по известной теореме Бёрка выдаёт независимый пуассоновский поток. Это исключение, как можно догадаться, в основном и используется.
Соединение двух пуассоновских потоков — пуассоновский поток. Вероятностное разделение пуассоновского потока на два — опять даёт два пуассоновских потока. Всё это приводит к тому, что все очереди в системе как бы независимы, и можно получить, выражаясь формальным языком, так называемое product-form solution. То есть совместное распределение длин очередей является просто произведением распределений длин всех очередей, рассматриваемых по отдельности — именно так в теории вероятностей выражается независимость. Просто находим входные потоки во все узлы и используем формулы для каждого узла независимо. Есть ряд ограничений:
- Вероятностный алгоритм маршрутизации. Запрос, обслуженный узлом, выбирает следующий случайно с известной вероятностью. Это не так плохо, как может показаться, потому что есть возможность использовать «классы запросов»: сказать, что все запросы Васи приходят в сервер № 1, потом в сервер № 2 и потом выходят из сети, а запросы Пети приходят в сервер № 2, а потом с равной вероятностью посещают сервер № 1 или № 3 и выходят. То есть не все переходы обязаны быть случайными, некоторые или даже все могут иметь 100%-ную вероятность.
- Предположение независимости Клейнрока. Время обработки запроса не может зависеть от истории или класса запроса, а определяется только сервером, а при повторном прохождении запроса через один и тот же сервер каждый раз выбирается случайно. Фактически отсутствует возможность задавать размеры запроса, который бы использовался в разных серверах, а время обслуживания определяется только самим сервером. Это ограничение тоже можно пытаться обойти. Для этого обычно используют вероятностную маршрутизацию и делают петлю для возврата в тот же сервер с некоторой вероятностью — как бы перезапускают запрос. На мой взгляд, это довольно странный трюк, ведь такой запрос повторно встаёт в очередь, а не выполняется сразу, но для некоторых задач это не важно.
- Пуассоновский входной трафик и экспоненциальное время обслуживания на всех узлах.
Стоит отметить, что при наличии обратной связи НЕ получается пуассоновский поток, так как потоки оказываются взаимозависимыми. На выходе из узла с обратной связью тоже получается непуассоновский поток, и в итоге все потоки становятся непуассоновскими. Однако удивительным образом оказывается, что все эти непуассоновские потоки ведут себя ровно так же, как пуассоновские (ох уж эта теория вероятностей), если выполняются указанные выше ограничения. И тогда мы опять получаем product-form solution. Такие сети имеют название Jackson networks, в них возможны обратные связи и, следовательно, множественные посещения любого сервера. Есть и другие сети, в которых позволяется больше вольностей, но в результате все значимые аналитические достижения теории массового обслуживания по отношению к сетям предполагают пуассоновские потоки на входе и product-form solution, что стало предметом критики этой теории и привело в 90-х как к разработке других теорий, так и к изучению того, какие на самом деле распределения нужны и как с ними работать.
Важное применение всей этой теории сетей Джексона — моделирование пакетов в IP-сетях и ATM-сетях. Модель достаточно адекватна: размеры пакетов не сильно меняются и не зависят от самого пакета, только от ширины канала, так как время обслуживания соответствует времени передачи пакета в канал. Случайное время отправки, хоть и звучит дико, на самом деле обладает не очень большой вариативностью. Более того, оказывается, что в сети с детерминированным временем обслуживания латентность не может быть больше, чем в аналогичной сети Джексона, поэтому такие сети смело можно использовать для оценки времени отклика сверху.
Неэкспоненциальные распределения
Все результаты, о которых я рассказал, относились к экспоненциальным распределениям, но я также упомянул, что реальные распределения отличаются. Возникает ощущение, что вся эта теория достаточно бесполезна. Это не совсем так. Есть способ встроить в этот математический аппарат и другие распределения, более того, практически любые распределения, но это будет кое-чего нам стоить. За исключением нескольких интересных случаев, теряется возможность получить решение в явном виде, теряется product-form solution, а вместе с ним конструктор: каждую задачу нужно решать целиком с нуля, используя цепи Маркова. Для теории это большая проблема, но на практике это просто означает применение численных методов и даёт возможность решать куда более сложные и приближенные к реальности задачи.
Метод фаз
Идея проста. Цепи Маркова не позволяют нам иметь память внутри одного состояния, поэтому все переходы должны быть случайными с экспоненциальным распределением времени между двумя преходами. Но что если состояние разбить на несколько подсостояний? Переходы между подсостояниями по-прежнему должны иметь экспоненциальное распределение, если мы хотим, чтобы вся конструкция оставалась цепью Маркова, а мы этого очень хотим, поскольку знаем, как решать такие цепи. Подсостояния часто называют фазами, если они выстроены последовательно, а процесс разбиения — методом фаз.
Самый простой пример. Обработка запроса выполняется в несколько фаз: сначала мы, например, читаем нужные данные из базы, затем выполняем какие-нибудь вычисления, потом записываем результаты в базу. Допустим, все эти три стадии имеют одинаковое экспоненциальное распределение времени. Какое распределение имеет время прохождения всех трёх фаз вместе? Это распределение Эрланга.
А что если сделать много-много коротких одинаковых фаз? В пределе получим детерминированное распределение. То есть, выстраивая цепочку, можно уменьшать вариативность распределения.
Можно ли увеличить вариативность? Легко. Вместо цепочки фаз используем альтернативные категории, случайно выбирая одну из них. Пример. Почти все запросы выполняются быстро, но есть небольшая вероятность, что придёт огромный запрос, который выполняется долго. Такое распределение будет иметь убывающий failure rate. Чем дольше мы ждём, тем больше вероятность, что запрос попал во вторую категорию.
Продолжая развивать метод фаз, теоретики выяснили, что есть класс распределений, с помощью которых можно приблизиться с любой точностью к произвольному неотрицательному распределению! Coxian distibution строится методом фаз, только мы не обязаны проходить все фазы, после каждой фазы есть некоторая вероятность завершения.
Такого рода распределения можно использовать как для генерации непуассоновского входного потока, так и для создания неэкспоненциального времени обслуживания. Вот, например, цепь Маркова для системы M/E2/1 с распределением Эрланга для времени обслуживания. Состояние определяется парой чисел (n, s), где n — длина очереди, а s — номер стадии, в которой находится сервер: первая или вторая. Возможны все комбинации n и s. Входящие сообщения меняют только n, а по завершении фаз происходит их чередование и уменьшение длины очереди после завершения второй фазы.
У вас микробёрсты!
Может ли тормозить система, загруженная вполовину своей мощности? В качестве первого подопытного препарируем M/G/1. Дано: пуассоновский поток на входе и произвольное распределение времени обслуживания. Рассмотрим путь одного запроса через всю систему. Случайно поступающий входящий запрос видит в очереди перед собой среднее по времени число запросов
. Среднее время обработки каждого из них . С вероятностью, равной утилизации , в сервере есть ещё один запрос, который нужно сначала «дообслужить» за время . Суммируя, получаем, что полное время ожидания в очереди . По теореме Литтла ; комбинируя, получаем: ![$\mathbf{E}[T_Q] = \frac{\rho}{1-\rho} \mathbf{E}[S_e]$](https://habrastorage.org/getpro/habr/formulas/e4a/afe/21c/e4aafe21cf6cece4d47f9c90088a57af.svg)
, видит, что на дообслуживание нужно время . 
Среднее время
определяется средним значением функции , то есть площадью треугольников, делённой на общее время. Понятно, что можно ограничиться одним «средним» треугольником, тогда . Это довольно неожиданно. Мы получили, что время дообслуживания определяется не только средним значением времени обслуживания, но и его вариативностью. Объяснение простое. Вероятность попасть в длинный интервал больше, она на самом деле пропорциональна длительности S этого интервала. Это объясняет знаменитый Waiting Time Paradox, или Inspection Paradox. Но вернёмся к M/G/1. Если скомбинировать всё, что мы получили, и переписать, используя вариативность , получим известную формулу Pollaczek-Khinchine: ![$\mathbf{E}[T_Q]=\frac{\rho}{1-\rho}\frac{\mathbf{E}[S]}{2}(C^2_S+1)$](https://habrastorage.org/getpro/habr/formulas/714/394/adb/714394adb7f758cb68a7c16c98f35ef9.svg)
. Это, согласитесь, намного больше, чем для экспоненциального распределения. В среднем всё выполняется супер быстро: . Теперь предположим, что RTMR моделируется системой M/G/1, и пусть система будет не сильно загружена, утилизация . Подставляя в формулу, получим . Из-за микробёрстов даже такая быстрая и недоутилизированная система может превратиться в среднем в отвратительную. За 50 мс можно 6 раз сходить на жёсткий диск или, если повезёт, даже в дата-центр на другом континенте! Кстати, для G/G/1 существует аппроксимация, которая учитывает вариативность поступающего трафика: она выглядит точно так же, только вместо в ней сумма обоих вариативностей . Для случая с несколькими серверами дела обстоят лучше, но эффект нескольких серверов влияет только на первый множитель. Эффект вариативности остаётся: .Как выглядят микробёрсты? Применительно к тредпулам это задачи, которые обслуживаются достаточно быстро, чтобы не быть заметными на графиках утилизации, и достаточно медленно, чтобы создать очередь за собой и влиять на время отклика пула. С точки зрения теории — это огромные запросы из хвостовой части распределения. Скажем, у вас пул из 10 тредов, и вы смотрите на график утилизации, построенный по метрикам времении работы и времени простоя, которые собираются раз в 15 секунд. Вы, во-первых, можете не заметить, что один тред вообще завис, или что все 10 тредов выполняли одновременно большие задачи целую секунду, а потом 14 секунд ничего не делали. Разрешающая способность в 15 секунд не позволяет увидеть скачок утилизации до 100% и обратно до 0%, а время отклика страдает. Например, так может выглядеть микробёрст, случающийся раз в 15 секунд в пуле из 6 потоков, если посмотреть на него через микроскоп.
В качестве микроскопа используется система трассировки, регистрирующая время событий (поступление и завершение запросов) с точностью до циклов процессора.
Специально чтобы разбираться с подобными ситуациями, в RTMR используется механизм SelfPing, который строго периодически (каждые 10 мс), отправляет маленькую задачу в тредпул с единственной целью — замерить время ожидания в очереди. Предполагая худший случай, к этому замеру добавляется период 10 мс и берётся максимум на окне в 15 секунд. Таким образом, мы получаем оценку сверху на максимальное время ожидания на окне. Да, мы не видим реального положения дел, если время отклика меньше 10 мс, но в этом случае мы можем считать, что всё хорошо — нет ни единого микробёрста. Зато эта дополнительная self-ping-активность съедает строго ограниченное количество CPU. Механизм удобен тем, что он универсальный и неинвазивный: не нужно менять ни код тредпула, ни код задач, которые в нём выполняются. Подчеркну: измеряется именно худший случай, что очень удобно и интуитивно, по сравнению со всякими перцентилями. Также механизм обнаруживает и другую похожую ситуацию: одновременный приход большого количества вполне обычных запросов. Если их не настолько много, чтобы проблему было видно на 15-секундных графиках утилизации, — это тоже можно считать микробёрстом.
Хорошо, а как быть, если SelfPing показывает, что происходит нечто неадекватное? Как найти виновных? Для этого мы используем трассировку, уже упомянутый LWTrace. Идём на проблемную машину и через мониторинг запускаем трассировку, которая отслеживает в нужном тредпуле все задачи и сохраняет в памяти только медленные. Затем можно посмотреть топ-100 медленных трасс. После кратковременного исследования трассировку выключаем. Все другие способы поиска виновных не подходят: писать логи на все задачи тредпула невозможно; писать только медленные задачи — тоже не самое лучшее решение, так как всё равно придётся собирать трассу для всех задач, а это тоже накладно; профилирование с помощью perf не поможет, так как тяжёлые задачи случаются слишком редко, чтобы быть заметными в профиле.
Независимость от распределения времени обслуживания
У нас осталась ещё одна «степень свободы», которую мы до сих пор не использовали. Входящий поток и размеры запросов мы обсудили, разные количества серверов тоже, но ещё не говорили о планировщиках. Все примеры подразумевали FIFO-обработку. Как я уже упоминал, планирование действительно влияет на время отклика системы, и правильный планировщик может значительно улучшить latency (алгоритмы SPT и SRPT). Но планирование — это очень продвинутая тема для теории массового обслуживания. Возможно, эта теория даже не очень хорошо подходит для исследования планировщиков, но это единственная теория, которая может давать ответы про стохастические системы с планировщиками и позволяет вычислять средние значения. Есть другие теории, которые позволяют многое понять про планирование «в худшем случае», но про них мы поговорим в другой раз.А сейчас рассмотрим несколько интересных исключений из общего правила, когда всё-таки удаётся получить product-form solution для сети и можно создать удобный конструктор. Начнём с одного узла M/Cox/1/PS. Пуассоновский поток на входе, практически произвольное распределение (Coxian distribution) времени обслуживания и справедливый планировщик (Processor Sharing), обслуживающий все запросы одновременно, но со скоростью, обратно пропорциональной их текущему числу. Где можно встретить такую систему? Например, именно так работают справедливые планировщики процессов в операционных системах. На первый взгляд может показаться, что это сложная система, но если построить (см. раздел метод фаз) и решить соответствующую цепь Маркова, то оказывается, что распределение длины очереди в точности повторяет систему M/M/1/FIFO, в которой время обслуживания имеет такое же среднее значение, но распределено экспоненциально.
Это невероятный результат! В противоположность тому, что мы видели в разделе про микробёрсты, здесь вариативность времени обслуживания никак не влияет на время отклика, ни в каком из перцентилей! Такое свойство редко встречается и называется insensitivity property. Обычно оно возникает в системах, где нет ожидания, и запрос сразу начинает так или иначе выполняться, когда не нужно дожидаться дообслуживания того, что уже выполняется. Другой пример системы с таким свойством — M/M/∞. В ней тоже нет ожидания, так как число серверов бесконечно. В таких системах выходной поток из узла имеет хорошее распределение, что позволяет получить product-form solution для сетей с такими серверами — сетей BCMP.
Для полноты картины рассмотрим простейший пример. Два сервера, работающие с разной средней скоростью (например, частота процессора отличается), произвольное распределение размеров поступающих задач, обслуживающий сервер выбирается случайно, бóльшая часть задач идёт на быстрый сервер. Нужно найти среднее время отклика. Решение. . Применим известную формулу для среднего времени отклика M/M/1/FCFS и получим .Ну всё, теперь и планирование обсудили, можно закругляться. В следующей статье я расскажу, как в системах реального времени подходят к вопросу латентности и какие концепции используются там.
Что почитать и посмотреть
- Изучение теории массового обслуживания всегда сопровождается довольно забористой математикой, и часто системы, которые рассматривают, не имеют никакого отношения к computer science, поэтому сложно найти хороший учебник. Я бы посоветовал Performance Modeling and Design of Computer Systems: Queueing Theory in Action (2013). Тут по-прежнему достаточно математики, но вся она приложена к интересным системам. Бóльшая часть данной статьи — вольный пересказ этой книги.
- Самое простое, насколько это возможно без потери смысла, изложение классики теории, о котором я знаю, в формате видеолекций у Robert B. Cooper. В этих лекциях он весьма доходчиво рассказывает практически всю свою книгу и всё, что требуется для её понимания.