Резервуарная выборка (eng. «reservoir sampling») — это простой и эффективный алгоритм случайной выборки некоторого количества элементов из имеющегося вектора большого и/или неизвестного заранее размера. Я не нашел об этом алгоритме ни одной статьи на Хабре и поэтому решил написать её сам.
Итак, о чём же идёт речь. Выбрать один случайный элемент из вектора — это элементарная задача:
Задача «вернуть K случайных элементов из вектора размером N» уже хитрее. Здесь уже можно ошибиться — например, взять K первых элементов (это нарушит требование случайности) или взять каждый из элементов с вероятностью K/N (это нарушит требование взять ровно K элементов). Кроме того, можно реализовать и формально корректное, но крайне неэффективное решение «перемешать случайно все элементы и взять K первых». И всё становится ещё интереснее, если добавить условие того, что N — число очень большое (нам не хватит памяти сохранить все N элементов) и/или н�� известно заранее. Для примера представим себе, что у нас есть какой-то внешний сервис, присылающий нам элементы по одному. Мы не знаем сколько их придёт всего и не можем сохранить их все, но хотим в любой момент времени иметь набор из ровно K случайно выбранных элементов из уже полученных.
Алгоритм резервуарной выборки позволяет решить эту задачу за O(N) шагов и O(K) памяти. При этом не требуется знать N заранее, а условие случайности выборки ровно K элементов будет чётко соблюдено.
Пусть K=1, т.е. нам нужно выбрать всего один элемент из всех пришедших — но так, чтобы у каждого из пришедших элементов была одинаковая вероятность быть выбранным. Алгоритм напрашивается сам собой:
Шаг 1: Выделяем память на ровно один элемент. Сохраняем в неё первый пришедший элемент.

Пока всё ок — нам пришел всего один элемент, с вероятностью в 100% (на данный момент) он должен являться выбранным — так и есть.
Шаг 2: Второй пришедший элемент с вероятностью 1/2 перезаписываем в качестве выбранного.

Здесь тоже всё хорошо: нам пока пришло только два элемента. Первый остался выбранным с вероятностью 1/2, второй перезаписал его с вероятностью 1/2.
Шаг 3: Третий пришедший элемент с вероятностью 1/3 перезаписываем в качестве выбранного.
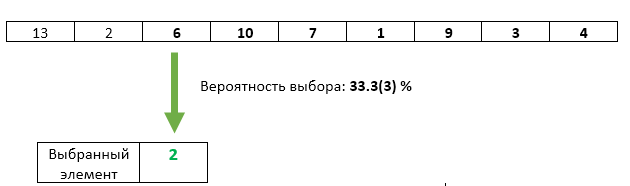
С третьим элементом всё хорошо — его шанс быть выбранным равен ровно 1/3. Но не нарушили ли мы каким-либо образом равенство шансов предыдущих элементов? Нет. Вероятность того, что на этом шаге выбранный элемент не будет перезаписан равна 1 — 1/3 = 2/3. А поскольку на шаге 2 мы гарантировали равенство шансов каждого из элементов быть выбранным, то после шага 3 каждый из них может оказаться выбранным с шансом 2/3 * 1/2 = 1/3. Ровно такой же шанс, как и у третьего элемента.
Шаг N: С вероятностью 1/N элемент номер N перезаписываем в качестве выбранного. У каждого из предыдущих пришедших элементов остаётся тот же шанс 1/N остаться выбранным.
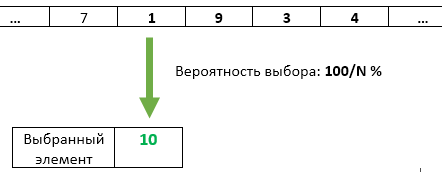
Но это была упрощённая задача, при K=1.
Шаг 1: Выделяем память на K элементов. Записываем в неё первые K пришедших элементов.

Единственный способ взять K элементов из K пришедших элементов — это взять их все :)
Шаг N: (для каждого N > K): генерируем случайное число X от 1 до N. Если X > K то отбрасываем данный элемент и переходим к следующему. Если X <= K, то перезаписываем элемент под номером X. Поскольку значение X будет равномерно случайно на диапазоне от 1 до N, то при условии X <= K оно будет равномерно случайно и на диапазоне от 1 до K. Таким образом мы обеспечиваем равномерность выбора перезаписываемых элементов.
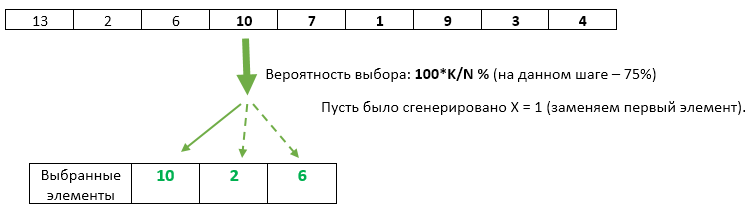
Как можно заметить — каждый следующий пришедший элемент имеет всё меньшую и меньшую вероятность быть выбранным. Она, тем ни менее, всегда будет равна ровно K/N (как и для каж��ого из предыдущих пришедших элементов).
Плюс этого алгоритма в том, что мы можем в любой момент времени остановиться, показать пользователю текущий вектор K — и это будет вектор честно выбранных случайных элементов из пришедшей последовательности элементов. Возможно, пользователя это устроит, а возможно, он захочет продолжить обработку входящих значений — мы можем это сделать в любой момент. При этом, как упоминалось в начале, мы никогда не используем больше, чем О(K) памяти.
Ах да, совсем забыл, в стандартную библиотеку С++17 наконец вошла функция std::sample, делающая ровно то, что описано выше. Стандарт не обязывает её использовать именно резервуарную выборку, но обязывает работать за O(N) шагов — ну и вряд ли разработчики её реализации в стандартной библиотеке выберут какой-то алгоритм, использующий более, чем О(K) памяти (а меньше тоже не получится — результат же нужно где-то хранить).
Итак, о чём же идёт речь. Выбрать один случайный элемент из вектора — это элементарная задача:
// C++ std::random_device rd; std::mt19937 gen(rd()); std::uniform_int_distribution<> dis(0, vect.size() — 1); auto result = vect[dis(gen)];
Задача «вернуть K случайных элементов из вектора размером N» уже хитрее. Здесь уже можно ошибиться — например, взять K первых элементов (это нарушит требование случайности) или взять каждый из элементов с вероятностью K/N (это нарушит требование взять ровно K элементов). Кроме того, можно реализовать и формально корректное, но крайне неэффективное решение «перемешать случайно все элементы и взять K первых». И всё становится ещё интереснее, если добавить условие того, что N — число очень большое (нам не хватит памяти сохранить все N элементов) и/или н�� известно заранее. Для примера представим себе, что у нас есть какой-то внешний сервис, присылающий нам элементы по одному. Мы не знаем сколько их придёт всего и не можем сохранить их все, но хотим в любой момент времени иметь набор из ровно K случайно выбранных элементов из уже полученных.
Алгоритм резервуарной выборки позволяет решить эту задачу за O(N) шагов и O(K) памяти. При этом не требуется знать N заранее, а условие случайности выборки ровно K элементов будет чётко соблюдено.
Начнём с упрощённой задачи
Пусть K=1, т.е. нам нужно выбрать всего один элемент из всех пришедших — но так, чтобы у каждого из пришедших элементов была одинаковая вероятность быть выбранным. Алгоритм напрашивается сам собой:
Шаг 1: Выделяем память на ровно один элемент. Сохраняем в неё первый пришедший элемент.

Пока всё ок — нам пришел всего один элемент, с вероятностью в 100% (на данный момент) он должен являться выбранным — так и есть.
Шаг 2: Второй пришедший элемент с вероятностью 1/2 перезаписываем в качестве выбранного.

Здесь тоже всё хорошо: нам пока пришло только два элемента. Первый остался выбранным с вероятностью 1/2, второй перезаписал его с вероятностью 1/2.
Шаг 3: Третий пришедший элемент с вероятностью 1/3 перезаписываем в качестве выбранного.

С третьим элементом всё хорошо — его шанс быть выбранным равен ровно 1/3. Но не нарушили ли мы каким-либо образом равенство шансов предыдущих элементов? Нет. Вероятность того, что на этом шаге выбранный элемент не будет перезаписан равна 1 — 1/3 = 2/3. А поскольку на шаге 2 мы гарантировали равенство шансов каждого из элементов быть выбранным, то после шага 3 каждый из них может оказаться выбранным с шансом 2/3 * 1/2 = 1/3. Ровно такой же шанс, как и у третьего элемента.
Шаг N: С вероятностью 1/N элемент номер N перезаписываем в качестве выбранного. У каждого из предыдущих пришедших элементов остаётся тот же шанс 1/N остаться выбранным.

Но это была упрощённая задача, при K=1.
Как изменится алгоритм при K>1 ?
Шаг 1: Выделяем память на K элементов. Записываем в неё первые K пришедших элементов.

Единственный способ взять K элементов из K пришедших элементов — это взять их все :)
Шаг N: (для каждого N > K): генерируем случайное число X от 1 до N. Если X > K то отбрасываем данный элемент и переходим к следующему. Если X <= K, то перезаписываем элемент под номером X. Поскольку значение X будет равномерно случайно на диапазоне от 1 до N, то при условии X <= K оно будет равномерно случайно и на диапазоне от 1 до K. Таким образом мы обеспечиваем равномерность выбора перезаписываемых элементов.

Как можно заметить — каждый следующий пришедший элемент имеет всё меньшую и меньшую вероятность быть выбранным. Она, тем ни менее, всегда будет равна ровно K/N (как и для каж��ого из предыдущих пришедших элементов).
Плюс этого алгоритма в том, что мы можем в любой момент времени остановиться, показать пользователю текущий вектор K — и это будет вектор честно выбранных случайных элементов из пришедшей последовательности элементов. Возможно, пользователя это устроит, а возможно, он захочет продолжить обработку входящих значений — мы можем это сделать в любой момент. При этом, как упоминалось в начале, мы никогда не используем больше, чем О(K) памяти.
Ах да, совсем забыл, в стандартную библиотеку С++17 наконец вошла функция std::sample, делающая ровно то, что описано выше. Стандарт не обязывает её использовать именно резервуарную выборку, но обязывает работать за O(N) шагов — ну и вряд ли разработчики её реализации в стандартной библиотеке выберут какой-то алгоритм, использующий более, чем О(K) памяти (а меньше тоже не получится — результат же нужно где-то хранить).
Материалы по теме
- Доклад разработчика из Facebook о том, как резервуарная выборка была использована в их движке поиска по внутренней кодовой базе (с 34-ой минуты).
- Статья в Википедии
- std::sample на Cppreference
