Решая упражнения к книге «Программируем коллективный разум», я решил поделиться реализацией одного из алгоритмов упомянутого в этой книге (Глава 2 — Упражнение 1).
Исходные условия следующие: пусть мы имеем словарь с оценками критиков:
Чем выше оценка, тем больше нравится фильм.
Надо вычислить: насколько схожи интересы критиков для того, например, чтобы можно было на основе оценок одного рекомендовать фильмы другому?
Коэффициент Танимото – описывает степень схожести двух множеств. В интернете я нашел несколько вариантов формулы для его вычисления. И решил остановиться на следующем:
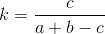
, где k — коэффициент Танимото (число от 0 до 1), чем он ближе к 1, тем более схожи множества;
a — количество элементов в первом множестве;
b — количество элементов во втором множестве;
c — количество общих элементов в двух множествах;
Теперь нам надо сравнить оценки двух критиков.
Сразу хочу прояснить один момент. Что следует считать общим элементом в двух наших множествах? Понятно, что представление оценки в текущем виде не позволит достаточно точно определить людей со схожими интересами. Ведь, по сути своей, одинаковые оценки 3,5 и 4.0 для этого алгоритма — совершенно разные цифры. Поэтому коэффициент Танимото, на мой взгляд, стоит использовать, если количество вариантов оценок не больше 2-3 (например, «понравилось-не понравилось» или «рекомендую-не смотрел-не рекомендую») Я решил немного изменить словарь для более удобной работы и применил к оценкам следующее преобразование: Если оценка меньше 3, значит фильм не понравился (оценка становится — 0), иначе – понравился (оценка становится — 1). Данные в таком виде являются более подходящими для нашего эксперимента.
На выходе мы получим следующий словарь:
А затем мы напишем функцию, которая вычисляет коэффициент сходства оценок двух критиков.
Проверим работоспособность функции tanimoto.
>>>print tanimoto(critics, 'Gene Seymour', 'Lisa Rose')
>>>0.5
По моему, результат верен. Надо заметить, что при увеличении количества оценок у каждого критика, увеличится и точность подсчета коэффициента сходства.
Если бы у нас была база данных оценок, можно было бы подсчитать коэффициенты сходства интересов людей и начинать давать рекомендации по методу Танимото.
Скачать текст примера можно тут.
Скачать полный текст всех примеров из книги можно на сайте автора. Там же можно найти более полный массив с оценками критиков.
Исходные условия следующие: пусть мы имеем словарь с оценками критиков:
critics={'Lisa Rose': {'Superman Returns': 3.5, 'You, Me and Dupree': 2.5, 'The Night Listener': 3.0},
'Gene Seymour': {'Superman Returns': 5.0, 'The Night Listener': 3.5, 'You, Me and Dupree': 3.5}}
Чем выше оценка, тем больше нравится фильм.
Надо вычислить: насколько схожи интересы критиков для того, например, чтобы можно было на основе оценок одного рекомендовать фильмы другому?
Коэффициент Танимото – описывает степень схожести двух множеств. В интернете я нашел несколько вариантов формулы для его вычисления. И решил остановиться на следующем:
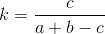
, где k — коэффициент Танимото (число от 0 до 1), чем он ближе к 1, тем более схожи множества;
a — количество элементов в первом множестве;
b — количество элементов во втором множестве;
c — количество общих элементов в двух множествах;
Теперь нам надо сравнить оценки двух критиков.
Сразу хочу прояснить один момент. Что следует считать общим элементом в двух наших множествах? Понятно, что представление оценки в текущем виде не позволит достаточно точно определить людей со схожими интересами. Ведь, по сути своей, одинаковые оценки 3,5 и 4.0 для этого алгоритма — совершенно разные цифры. Поэтому коэффициент Танимото, на мой взгляд, стоит использовать, если количество вариантов оценок не больше 2-3 (например, «понравилось-не понравилось» или «рекомендую-не смотрел-не рекомендую») Я решил немного изменить словарь для более удобной работы и применил к оценкам следующее преобразование: Если оценка меньше 3, значит фильм не понравился (оценка становится — 0), иначе – понравился (оценка становится — 1). Данные в таком виде являются более подходящими для нашего эксперимента.
def prepare_for_tanimoto(critics_arr):
arr = critics_arr.copy()
for critic in arr:
for film in arr[critic]:
if arr[critic][film] < 3:
arr[critic][film] = 0
else:
arr[critic][film] = 1
return arr
На выходе мы получим следующий словарь:
critics={'Lisa Rose': {'Superman Returns': 1, 'You, Me and Dupree': 0, 'The Night Listener': 1},
'Gene Seymour': {'Superman Returns': 1, 'The Night Listener': 1, 'You, Me and Dupree': 1}}
А затем мы напишем функцию, которая вычисляет коэффициент сходства оценок двух критиков.
def tanimoto(critics_arr, critic1, critic2):
arr = prepare_for_tanimoto(critics_arr)
a = len(arr[critic1])
b = len(arr[critic2])
c = 0.0
for film in arr[critic1]:
if arr[critic1][film] == arr[critic2][film]:
c = c + 1
koef = c / (a + b - c)
return koef
Проверим работоспособность функции tanimoto.
>>>print tanimoto(critics, 'Gene Seymour', 'Lisa Rose')
>>>0.5
По моему, результат верен. Надо заметить, что при увеличении количества оценок у каждого критика, увеличится и точность подсчета коэффициента сходства.
Если бы у нас была база данных оценок, можно было бы подсчитать коэффициенты сходства интересов людей и начинать давать рекомендации по методу Танимото.
Скачать текст примера можно тут.
Скачать полный текст всех примеров из книги можно на сайте автора. Там же можно найти более полный массив с оценками критиков.