Не так давно прошёл конкурс параллельного программирования Acceler8 2011. Суть задачи заключалась в поиске максимальной подматрицы в данной матрице (сумма элементов найденной подматрицы должна быть максимальной). После недолгого «гугления» было найдено, что некий алгоритм Тадао Такаока решает эту задачу быстрее других.
«Вызов принят!», и я начала искать этот алгоритм везде, где только можно, задавшись целью реализовать его. Не смотря на то, что распараллеливается он плохо и в своей сложности содержит немаленькую константу.
Однако всё, что удалось найти, — статьи на английском этого самого Тадао Такаоки (вот одна из этих статей). Пришлось переводить.
Сама идея алгоритма сначала казалась до безобразия простой:
Вот, что написано по поводу нахождения этого самого решения в оригинальной статье:
"Теперь column-centered задача может быть решена следующим образом.
A_column = max(k=1:i-1,l=0:n/2-1,i=1:m,j=n/2+1:n) {s[i, j] − s[i, l] − s[k, j] + s[k, l]}.
Мы фиксируем i и k, и максимизируем оставшееся выражение изменением l и j. Тогда это эквивалентно следующему выражению:
i = 1, ..., m и k = 1, ..., i − 1.
A_column [i, k] = max(l=0:n/2-1,j=n/2+1:n) {−s[i, l] + s[k, l] + s[i, j] − s[k, j]}
Пусть s∗[i, j] = −s[j, i]. Тогда данное выражение может быть сведено к:
A_column [i, k] = −min(l=0:n/2-1) {s[i, l] + s∗ [l, k]} + max(j=n/2+1:n) {s[i, j] + s ∗[j, k]}"
Далее следует упоминуть о некой другой задаче Тадао Такаока: Distance Matrix Multiplication (не берусь переводить этот термин).
Суть такова:
Целью DMM является вычисление произведения расстояний(distance product) C = AB для двух n-мерных матриц A = а[i,j] and B = b[i,j], чьи элементы — вещественные числа.
c[i,j] = min(k=1:n) { a[i,k] + b[k,j] }
Суть c[i,j] — наименьшее расстояние из вершины i из первого слоя до вершины j в третьем слое в ациклическом ориентрированном графе, состоящем из трёх слоёв вершин. Эти вершины пронумерованы 1,...,n в каждом слое, и расстояние от i в первом слое до j во втором слое — a[i,j] и из i во втором слое до j в третьем слое — b[i,j]. Очевидно, что это выражение можно легко привести для подсчёта максимума вместо минимума — это будет задача о нахождении наибольших путей.
Так вот воспользовавшись этим определением можно получить следующее:
В формуле A_column [i, k] = −min(l=0:n/2-1) {s[i, l] + s∗ [l, k]} + max(j=n/2+1:n) {s[i, j] + s ∗[j, k]} видно, что первая часть формулы — DMM для минимума, вторая — DMM для максимума. Пусть S1 и S2 матрицы, чьи элементы (i, j) являются s[i, j − 1] s[i, j + n/2] соответственно. Для любой матрицы T, пусть T∗ — матрица, полученная из T транспонированием и отрицанием. Тогда верхнее выражение может быть посчитано «перемножением» S1 и S1∗ для минимума и получением нижне-треугольной матрицы, «перемножением» S2 и S2∗ для максимума и получением нижне-треугольной матрицы и, наконец, вычитанием из последней предыдущей матрицы. Вычислив в ней максимум, получим ответ:
A_column = max(DMM_max(S2*S2∗)-DMM_min(S1*S1∗)).
Далее преведен псевдокод для решения задачи DMM для матриц A и B размером nxn:
В статье рекомендуется использовать бинарную кучу для очередей. В более поздних версиях было указано, что использование фиббоначиевой кучи могло бы ещё больше ускорить процесс, однако я, к своему стыду, не смогла её реализовать в полной мере. Поэтому использовала бинарную.
Однако даже реализовав этот псевдокод, я обнаружила, что решение не работает. Очевидная ошибка была найдена на этапе вычисления S1 и S2 — описанного правила для построения этих матриц было недостаточно для правильной работы алгоритма. И ни в одной статье я более подробного описания не нашла. Таким образом строить матрицы пришлось самой.
Итак, после долгих часов, потраченных на перебор и проверку, были получены следующие правила.
Пусть S — префиксная матрица для матрицы A.
Тогда матрица S1 размерами m на n/2 содержит в себе первый столбец из 0, а оставшиеся n/2-1 столбцы содержат первые столбцы префиксной матрицы S:
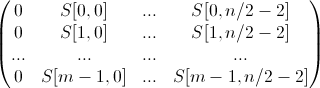
Матрица S1∗ размерами n/2 на m содержит первую строку и столбец из 0, оставшаяся подматрица представляет собой отрицание и транспонирование первых строк и столбцов префиксной матрицы S:

(k = n div 2 + n mod 2)
Матрица S2 размерами m на k содержит в себе столбцы префиксной матрицы S, начиная с k-го:

Матрица S2∗ размерами k на m: первый столбец из 0, далее — транспонирование и отрицание столбцов префиксной матрицы S, начиная с k-го столбца:

В целом алгоритм оказался очень сложным для понимания и реализации и не оправдал своих ожиданий на исключительную скорость(никаких дополнительных оптимизаций не осуществлялось).
В той же статье утверждается, что данный алгоритм работает за время O(n^3*log(log(n))/log(n)), а также упоминается, что алгоритм работает быстрее в сравнении с другими алгоритмами на матрицах большого размера (видимо, очень большого).
Если кому-то будет интересно или жизненно необходимо, здесь лежат исходники моей реализации (написано на плюсах, поэтому «понятности» не гарантирую). Буду очень рада, если эта статья кому-то поможет (не зря же я потратила столько времени на разбирательства с этим алгоритмом!).
«Вызов принят!», и я начала искать этот алгоритм везде, где только можно, задавшись целью реализовать его. Не смотря на то, что распараллеливается он плохо и в своей сложности содержит немаленькую константу.
Однако всё, что удалось найти, — статьи на английском этого самого Тадао Такаоки (вот одна из этих статей). Пришлось переводить.
Сама идея алгоритма сначала казалась до безобразия простой:
Для начала нам необходимо посчитать все префиксные суммы s[i, j] для таких матриц, как a[1..i, 1..j], для всех i и j с ограничением s[i, 0] = s[0, j] = 0. Очевидно, это делается за время O(mn).Если A_left и A_right находятся через рекурсию, то находить A_column надо вручную.
Основной алгоритм:
Если матрица оказывается одним элементом — возвращаем его значение.
Иначе:
Таким образом m ≤ n.
- если m > n, поворачиваем матрицу на 90 градусов.
- Пусть A_left — решение для левой половины.
- A_right — решение для правой половины.
- A_column — решение для column-centered задачи (нахождение такой максимальной подматрицы, которая бы пересекала центральную линию)
- Общее решение — максимум из этих трёх.
Вот, что написано по поводу нахождения этого самого решения в оригинальной статье:
"Теперь column-centered задача может быть решена следующим образом.
A_column = max(k=1:i-1,l=0:n/2-1,i=1:m,j=n/2+1:n) {s[i, j] − s[i, l] − s[k, j] + s[k, l]}.
Мы фиксируем i и k, и максимизируем оставшееся выражение изменением l и j. Тогда это эквивалентно следующему выражению:
i = 1, ..., m и k = 1, ..., i − 1.
A_column [i, k] = max(l=0:n/2-1,j=n/2+1:n) {−s[i, l] + s[k, l] + s[i, j] − s[k, j]}
Пусть s∗[i, j] = −s[j, i]. Тогда данное выражение может быть сведено к:
A_column [i, k] = −min(l=0:n/2-1) {s[i, l] + s∗ [l, k]} + max(j=n/2+1:n) {s[i, j] + s ∗[j, k]}"
Далее следует упоминуть о некой другой задаче Тадао Такаока: Distance Matrix Multiplication (не берусь переводить этот термин).
Суть такова:
Целью DMM является вычисление произведения расстояний(distance product) C = AB для двух n-мерных матриц A = а[i,j] and B = b[i,j], чьи элементы — вещественные числа.
c[i,j] = min(k=1:n) { a[i,k] + b[k,j] }
Суть c[i,j] — наименьшее расстояние из вершины i из первого слоя до вершины j в третьем слое в ациклическом ориентрированном графе, состоящем из трёх слоёв вершин. Эти вершины пронумерованы 1,...,n в каждом слое, и расстояние от i в первом слое до j во втором слое — a[i,j] и из i во втором слое до j в третьем слое — b[i,j]. Очевидно, что это выражение можно легко привести для подсчёта максимума вместо минимума — это будет задача о нахождении наибольших путей.
Так вот воспользовавшись этим определением можно получить следующее:
В формуле A_column [i, k] = −min(l=0:n/2-1) {s[i, l] + s∗ [l, k]} + max(j=n/2+1:n) {s[i, j] + s ∗[j, k]} видно, что первая часть формулы — DMM для минимума, вторая — DMM для максимума. Пусть S1 и S2 матрицы, чьи элементы (i, j) являются s[i, j − 1] s[i, j + n/2] соответственно. Для любой матрицы T, пусть T∗ — матрица, полученная из T транспонированием и отрицанием. Тогда верхнее выражение может быть посчитано «перемножением» S1 и S1∗ для минимума и получением нижне-треугольной матрицы, «перемножением» S2 и S2∗ для максимума и получением нижне-треугольной матрицы и, наконец, вычитанием из последней предыдущей матрицы. Вычислив в ней максимум, получим ответ:
A_column = max(DMM_max(S2*S2∗)-DMM_min(S1*S1∗)).
Далее преведен псевдокод для решения задачи DMM для матриц A и B размером nxn:
Copy Source | Copy HTML
- /Отсортировать n строк B в порядке убывания в списки list[i], т.о. в каждом списке list[i] будут находится индексы упорядоченных элементов строки i;
- /Заведём множество V = {1, ..., n};
- for i := 1 to n do begin
- for k := 1 to n do begin
- cand[k]:=first of list[k];
- d[k] := a[i, k] + b[k, cand[k]];
- end;
- / Упорядочим V как очередь с приоритетом по ключам d[1], ..., d[n];
- / Множество решений S - пустое;
- /* Фаза 1 : До критической точки */
- while |S| ≤ n − n log n do begin
- /Найти v с минимальным ключем в очереди;
- /Занести cand[v] в множество S;
- c[i, cand[v]] := d[v];
- /Пусть множество W = {w|cand[w] = cand[v]};
- for w in W do
- while cand[w] is in S do cand[w]:= next of list[w];
- /Отсортировать очередь W по новым ключам d[w] = a[i, w]+b[w, cand[w]];
- end;
- U := S;
- /* Фаза 2 : После критической точки */
- while |S| < n do begin
- /Найти v с минимальным ключём в очереди;
- if cand[v] is not in S then begin
- /Занести cand[v] в множество S;
- c[v, cand[v]] := d[v];
- /Пусть множество W = {w|cand[w] = cand[v]};
- end else W = {v};
- for w in W do
- cand[w]:=next of list[w];
- while cand[w] is in U do cand[w]:= next of list[w];
- /Отсортировать очередь W по ключам d[w] = a[i, w]+b[w, cand[w]];
- end;
- end.
В статье рекомендуется использовать бинарную кучу для очередей. В более поздних версиях было указано, что использование фиббоначиевой кучи могло бы ещё больше ускорить процесс, однако я, к своему стыду, не смогла её реализовать в полной мере. Поэтому использовала бинарную.
Однако даже реализовав этот псевдокод, я обнаружила, что решение не работает. Очевидная ошибка была найдена на этапе вычисления S1 и S2 — описанного правила для построения этих матриц было недостаточно для правильной работы алгоритма. И ни в одной статье я более подробного описания не нашла. Таким образом строить матрицы пришлось самой.
Итак, после долгих часов, потраченных на перебор и проверку, были получены следующие правила.
Пусть S — префиксная матрица для матрицы A.
Тогда матрица S1 размерами m на n/2 содержит в себе первый столбец из 0, а оставшиеся n/2-1 столбцы содержат первые столбцы префиксной матрицы S:
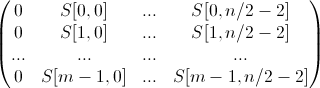
Матрица S1∗ размерами n/2 на m содержит первую строку и столбец из 0, оставшаяся подматрица представляет собой отрицание и транспонирование первых строк и столбцов префиксной матрицы S:

(k = n div 2 + n mod 2)
Матрица S2 размерами m на k содержит в себе столбцы префиксной матрицы S, начиная с k-го:

Матрица S2∗ размерами k на m: первый столбец из 0, далее — транспонирование и отрицание столбцов префиксной матрицы S, начиная с k-го столбца:

В целом алгоритм оказался очень сложным для понимания и реализации и не оправдал своих ожиданий на исключительную скорость(никаких дополнительных оптимизаций не осуществлялось).
В той же статье утверждается, что данный алгоритм работает за время O(n^3*log(log(n))/log(n)), а также упоминается, что алгоритм работает быстрее в сравнении с другими алгоритмами на матрицах большого размера (видимо, очень большого).
Если кому-то будет интересно или жизненно необходимо, здесь лежат исходники моей реализации (написано на плюсах, поэтому «понятности» не гарантирую). Буду очень рада, если эта статья кому-то поможет (не зря же я потратила столько времени на разбирательства с этим алгоритмом!).
