
Говоря «хаос», мы, обычно, подразумеваем полное отсутствие порядка, абсолютную неупорядоченность и случайность. С математической точки зрения, хаос и порядок – понятия не взаимоисключающие. Теория хаоса (есть что-то завораживающие в названиях математических теорий) – достаточно молодая математическая область, создание которой приравнивают по значимости открытий ХХ века к созданию квантовой механики. Хаос случается в нелинейных динамических системах. Иначе говоря, любой процесс, который протекает со временем, может быть хаотичным (например, высота дерева, температура тела или популяция мадагаскарских тараканов).
Чтобы разобраться, что такое хаос, сначала обратимся к системам, такой чертой не наделённым. Детерминированные системы не допускают никаких случайностей: значение на выходе полностью определено значениями на входе. Таким образом, изменение начальных условий вызывает пропорциональное изменение результата. Так, ньютоновская механика подразумевает детерминированность, и изменяя, к примеру, силу пинка по мячу, можно ожидать соответствующее изменение в продолжительности полёта этого мяча. Так что, по принципу детерминированности, положение мяча в текущий момент полностью определено положением мяча в предыдущий момент и будущее положение зависит от текущего и всё это совсем несложно посчитать. Так, и астрономы прошлого времени полностью доверялись этому принципу и считали, что вселенная – строго детерминированная система и положение небесных тел в будущем (и в прошлом) можно рассчитать, зная их текущее положение и скорость, т.е. зная начальные условия. Предполагалось, что чем точнее известны начальные условия, тем точнее будет результат прогноза, однако известный математик Анри Пуанкаре, который (в свободное время, вероятно) занимался описанием орбит небесных тел, обнаружил, что в системах из 3-х и более тел, при незначительном изменение начальных условий (положения и скорости), траектории тела очень быстро удаляются друг от друга. Два близких набора начальных условий давали различные результаты.
Большой вклад в теорию хаоса внёс метеоролог Эдвард Лоренц. В шестидесятых годах прошлого века этот американец работал над компьютерной программой, моделирующей движение воздушных масс в атмосфере Земли. Все мы знаем, что компьютер (вопреки расхожим слухам) является строго детерминированной системой, и это создаёт известный принцип «garbage in garbage out». Лоренц гонял свою программу и в хвост, и в гриву, получая всякие разные результаты. Некоторые его коллеги даже делали предположения, что эта модель является точным предсказателем погоды, спрашивали, брать ли завтра зонтик. Разумеется, эти выводы были поспешны, вскоре выяснилась одна особенность модели погоды. Один раз для ускорения вычислений, Лоренц запустил программу не сначала, а ввёл в неё данные из предыдущего «прогона», которые были распечатаны на бумаге. Однако результаты такого запуска быстро начали отклоняться от уже полученных, формируя абсолютно другую картину. Немного неожиданно, не так ли? Оказалось, что Лоренц вводил не точные результаты прошлых вычислений, а округлённые перед выводом на печать, эта погрешность просто игнорировалась. Модель Лоренца оказалась сверхчувствительна к начальным условиям. Малейшее различие во входных данных приводило к сильному расхождению результатов с течением времени. Эта зависимость от начальных условий и была названа хаосом. Лоренцом была озвучена знаменитая черта хаоса, именуемая «эффектом бабочки», который предполагает, что в зависимости от того, махнёт ли бабочка крыльями в лесах Бразилии зависит случится ли в Техасе ураган или нет. Этот же принцип был положен в основу одноимённого фильма с Эштоном Катчером (кино ненаучное, смотреть необязательно).

Отклонение в результатах повторных вычислений
Вся эта зависимость от начальных условий предполагает, что мы не можем делать долгосрочные прогнозы в нестабильных динамических системах. Любая погрешность в начальных условиях не позволит нам предсказать результат на какой-либо продолжительный отрезок времени. Если, к примеру, взять модель Лоренца, в качестве входных данных для определения скорости ветра нам будет необходимо ввести значения температуры и давления в каждой точке земной атмосферы, только тогда можно будет ожидать достоверный прогноз на длительный срок. Причём, входные данные должны быть абсолютно точными, т. е. с бесконечным числом знаков после запятой. А как известно, совершенно все измерительные приборы на Земле имеют ненулевую погрешность. Как бы точно не была измерена величина, всегда можно (теоретически) измерить точнее. Да и нет таких машин, которые бы позволили вводить бесконечное количество знаков после запятой. Может с приходом квантовых компьютеров что-то и изменится, не знаю.
Вот и выходит, что никуда от хаоса не деться и надо с ним мириться. Но не всё так плохо, на мой взгляд. Если бы все процессы во вселенной были бы полностью детерминированными, без единого намёка на случайность, жить было бы намного скучнее. Некоторые учёные даже склоняются к мысли о том, что хаос придаёт вселенной «стрелу времени», направленное и необратимое движение из прошлого в будущее.
Однако «хаос» и «случайность» понятия совсем не равнозначные. Определённая интерпретация процессов, кажущихся случайными, приводит их в порядок. К примеру, время между биени��ми сердца человека величина непостоянная, даже если человек не подвержен физ нагрузке. Если мы понаблюдаем за биением сердца некоторое время и интервалы между биениями запишем в таблицу, а также создадим второй столбец, копируя значения из первого, но со сдвигом на одно значение (т.е. первому измерению (t) в первом столбце будет соответствовать второе измерение (t+1) во втором, второму — третье и т.д;), можно будет построить карту, где по вертикали будем иметь значения без сдвига (t), а по горизонтали — значения со сдвигом(t+1). Точки на этой карте не будут рассыпаны в случайном порядке, а будут притянуты к некой области, формируя аттрактор.
Распространённый пример хаотической системы – это двойной маятник, т.е. маятник, к концу которого прикреплен второй маятник. Вы, возможно, видели подобные маятники в магазинах подарков. Так вот если взять два одинаковых маятника, поставить рядом и отклонить их приблизительно на равную величину, то уже через несколько колебаний маятники полностью рассинхронизируются. Чем точнее мы будем соблюдать начальные условия, тем дольше маятники будут качаться в такт, однако от расходимости никуда не деться.

Такие узоры рисует лампочкой на двойном маятнике художник Джордж Иоаннидис
Долгое время теория хаоса считалась некой математической абстракцией, не имеющей подтверждения в реальных условиях. Эта проблема волновала одного японца по имени Леон Чуа, который был нацелен показать, что хаос можно создать. Для этой цели он собрал электрическую цепь.
Цепь Чуа явилась первой электрической цепью, способной генерировать хаотические сигналы. Его творение было гениально в своей простоте, цепь состояла из четырёх линейных элементов: двух конденсаторов, одной индуктивности и резистора, а также включала в себя один нелинейный локально активный элемент, на кусочно-линейной вольт-амперной характеристике которого имелась область с негативным сопротивлением. Этот элемент теперь часто называют диодом Чуа. Цепь представляет собой генератор, и диод Чуа является необходимой частью для достижения хаотических колебаний. Этот элемент недоступен как отдельный компонент, но его несложно собрать, задействовав два операционных усилителя. Другие способы реализации этой нелинейности включают в себя встречно-параллельно подключенную пару инверторов или туннельный диод (похоже, всё-таки доступен, как отдельный компонент), на ВАХ которого, как известно, имеется «долина».
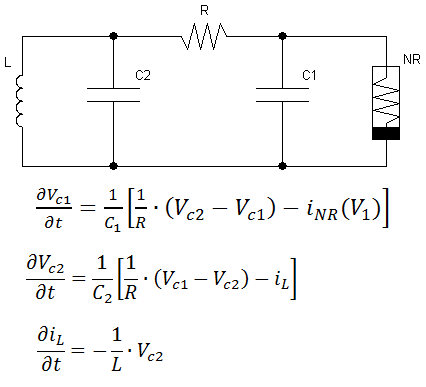
Обобщённая схема генератора Чуа и уравнения, его описывающие
Математика за всем этим стоит довольно сложная, но если не вдаваться в дебри, то эта цепь описывается тремя дифференциальными уравнениями, показывающими изменение по времени напряжения на двух конденсаторах и тока через индуктивность. Численное решение этих уравнений показывает, что при определённых соотношениях между компонентами цепи, изменение значений переменных во времени приобретает хаотический характер.
Собрать генератор Чуа труда особого не составляет. Эта цепь может демонстрировать такие явления хаоса как бифуркации и хаотический аттрактор. Однако для наблюдения всех этих чудес, будет необходим осциллограф, да ещё с двумя входами. В классическом варианте, схема состоит из двух конденсаторов, одной индуктивности, семи резисторов, микросхемы с парой операционных усилителей и двух батареек на 9В (можно использовать блок питания, но питание должно быть двухполярным). Для достижения хаотического поведения, между номиналами элементов должны соблюдаться определённые соотношения. Так, ёмкость конденсатора С2 должна быть примерно 10 ёмкостей С1, отношение С2/С1 называют α. Коэффициент β показывает отношение между R, C2 и L, а именно, β = R^2 C2 / L и должен равняться приблизительно 15.
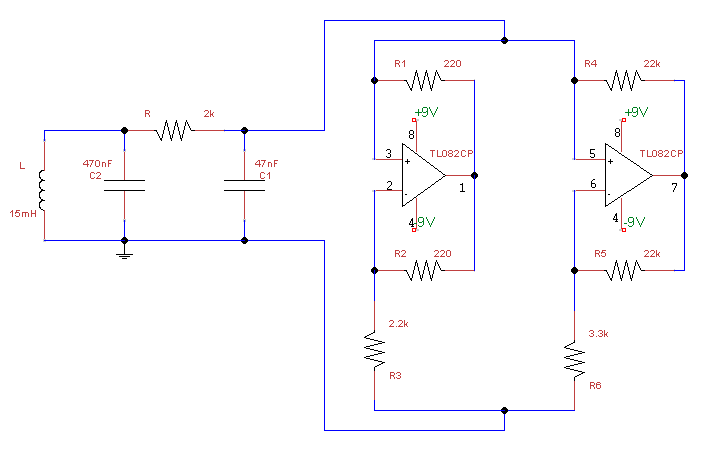
Принципиальная схема генератора с отрицательным сопротивлением на операционных усилителях
Итак, приступим к сборке. Собирать можно и на макетной плате, но чтобы сигналы были чётче, лучше компоненты спаять на печатной плате. В своей сборке я использовал конденсаторы на 47нФ и 470нФ, индуктивность на 15мГн и потенциометр на 1кОм (за неимением такового номиналом 2кОм, соединил его последовательно с резистором на 1кОм). Последовательно с индуктивностью можно (но необязательно) включить резистор малого номинала (до 10Ом), чтобы добавить «красоты» в сигналы. Диод Чуа реализован стандартным способом, с применением двух операционников. Я использовал микросхему TL082CP, по спецификации, это широкополосный операционный усилитель, советую использовать такой тип, с более простыми аналогами схема у меня не «завелась». Для создания характеристики с необходимыми наклонами, нам потребуются следующие номиналы резисторов: R1 = R2 = 220Ом, R3 = 2.2кОм, R4 = R5 = 22кОм, R6 = 3.3кОм. Запитать операционник можно двумя батарейками 9В, для корректной работы ОУ питание нам нужно двухполярное. Моя сборка топорная, согласен — проводки под питание и скрученные резисторы, другие мелкие недочёты, но для мониторинга хаотических сигналов этого хватило.

Остальную часть платы сбережём для следующих проектов
После аккуратной сборки этой несложной схемы, можно попробовать посмотреть, что за сигналы она генерирует. Сигналы будем снимать с конденсаторов C1 и С2. На моей схеме я сделал два BNC разъёма для удобства подсоединения схемы к осциллографу. Подключаем кабели к осциллографу и выбираем X-Y режим, когда по одной оси у нас будет напряжение на первом конденсаторе, а по другой – напряжение на втором. Что вывести на X, а что на Y значения не имеет. Выкрутим ручку потенциометра на максимальное значение и запитаем схему. На экране осциллографа должна появиться точка. Медленно уменьшаем значение сопротивления (лучше использовать потенциометры с большим ходом и с крупной ручкой, дабы обеспечить плавность изменения сопротивления), в какой-то момент точка должна превратиться в орбиту. Последующее уменьшение сопротивления приводит к раздваиванию этой орбиты, мы начинаем наблюдать бифуркации. Удвоения периода орбиты будут происходить и дальше с уменьшением сопротивления, расстояния между последующими раздвоениями будут постоянно и планомерно уменьшаться. Т.е. разница сопротивлений между четверной и восьмерной орбитой будет меньше, чем между четверной и двойной. Скорость, с которой интервал между бифуркациями уменьшается определяется константой Фейгенбаума. Период, до которого вам удастся наблюдать бифуркации зависит от четкости сигналов (т.е. от качества соединений) и от чувствительности потенциометра (дрожание рук тоже не на пользу). В какой-то момент стабильная орбита уступает место двухпетлевому аттрактору, который знаменует наступление хаоса. Этот аттрактор имеет три точки равновесия: одну в начале координат, и две в «дырках» петель. Типичная траектория аттрактора начинает вращение вокруг одной из «дырок», удаляясь от точки равновесия с каждым витком, затем траектория либо возвращается ближе в центру и вновь удаляется, либо направляется к другой точке равновесия, где процесс повторяется. Количество вращений в каждом случае случайно.

Образование хаоса через бифуркации
Этот аттрактор будет существовать в некотором интервале сопротивлений, а затем уступит место стабильной орбите, показывающей гармонические колебания. При достаточно малых значениях сопротивления, цепь превращается в простой колебательный контур, генерирующий синусоидальный сигнал с частотой, определённой значениями конденсаторов и индуктивности. Для большей «гибкости» цепи, потенциометрами можно заменить резисторы в цепи отрицательного сопротивления.
Если мы взглянем на спектр сигналов, то увидим, что в хаотическом режиме полоса генерации достаточно широкая и не имеет ярко выраженных пиков, к тому же начинается с постоянной составляющей.

Спектр хаотического сигнала
Схема предельно проста, но её поведение изучалось многими учёными, работающими с теорией хаоса. С её помощью изучались бифуркации и создавалась целая галерея различных аттракторов. Однако кроме чисто научного интереса, данная схема имеет и практическое применение.
Поскольку это генератор, значит, его можно использовать для радиосвязи, а раз этот генератор необычный, радиосвязь можно сделать защищённой. Существует несколько типов модуляции хаотического сигнала, от простого маскирования информационного сигнала, до высокоуровневой цифровой модуляции. Высокая чувствительность хаотического генератора позволяет использовать его в качестве детектора слабых сигналов. Также сообщалось о создании генератора случайных чисел на основе данной схемы. Кроме того, как вы заметили, спектр данного генератора лежит в звуковом диапазоне, так что этой схемой не преминули воспользоваться концептуальные музыканты.
Не знаю, многие ли захотят собрать этот хаотический генератор, ибо практической пользы от него маловато, но, мне кажется, возможность поиграться с ним и понаблюдать интересные узоры на осциллографе стоит этих копеечных деталей и получаса времени. Даже если покупать все компоненты поштучно в магазине, 200 рублей – максимум, что можно потратить, но я уверен, что у многих все детали есть в загашниках!
Данная схема может быть интересна студентам математических и электротехнических факультетов. Думаю, что демонстрация работы генератора Чуа сможет заинтересовать преподавателей, в чьи научные интересы входит теория хаоса. Спасибо всем за внимание!
