Фильтр Калмана

В интернете, в том числе и на хабре, можно найти много информации про фильтр Калмана. Но тяжело найти легкоперевариваемый вывод самих формул. Без вывода вся эта наука воспринимается как некое шаманство, формулы выглядят как безликий набор символов, а главное, многие простые утверждения, лежащие на поверхности теории, оказываются за пределами понимания. Целью этой статьи будет рассказать об этом фильтре на как можно более доступном языке.
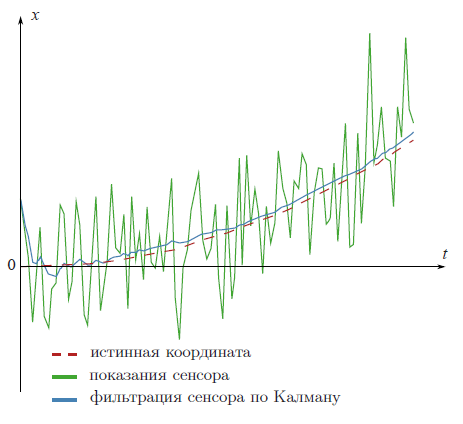
Фильтр Калмана — это мощнейший инструмент фильтрации данных. Основной его принцип состоит в том, что при фильтрации используется информация о физике самого явления. Скажем, если вы фильтруете данные со спидометра машины, то инерционность машины дает вам право воспринимать слишком быстрые скачки скорости как ошибку измерения. Фильтр Калмана интересен тем, что в каком-то смысле, это самый лучший фильтр. Подробнее обсудим ниже, что конкретно означают слова «самый лучший». В конце статьи я покажу, что во многих случаях формулы можно до такой степени упростить, что от них почти ничего и не останется.

Ликбез

Перед знакомством с фильтром Калмана я предлагаю вспомнить некоторые простые определения и факты из теории вероятностей.

Случайная величина

Когда говорят, что дана случайная величина 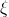, то имеют ввиду, что эта величина может принимать случайные значения. Разные значения она принимает с разной вероятностью. Когда вы кидаете, скажем, кость, то выпадет дискретное множество значений: . Когда речь идет, например, о скорости блуждающей частички, то, очевидно, приходится иметь дело с непрерывным множеством значений. «Выпавшие» значения случайной величины мы будем обозначать через но иногда, будем использовать ту же букву, которой обозначаем случайную величину:
В случае с непрерывным множеством значений случайную величину характеризует плотность вероятности , которая нам диктует, что вероятность того, что случайная величина «выпадет» в маленькой окрестности точки длиной равна . Как мы видим из картинки, эта вероятность равна площади заштрихованного прямоугольника под графиком:


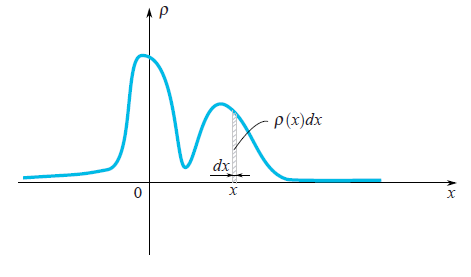
Довольно часто в жизни случайные величины распределены по Гауссу, когда плотность вероятности равна .

Мы видим, что функция имеет форму колокола с центром в точке и с характерной шириной порядка .
Раз мы заговорили о Гауссовом распределении, то грешно будет не упомянуть, откуда оно возникло. Также как и числа и прочно обосновались в математике и встречаются в самых неожиданных местах, так и распределение Гаусса пустило глубокие корни в теорию вероятностей. Одно замечательное утверждение, частично объясняющее Гауссово всеприсутствие, состоит в следующем:
Пусть есть случайная величина имеющая произвольное распределение (на самом деле существуют некие ограничения на эту произвольность, но они совершенно не жесткие). Проведем экспериментов и посчитаем сумму «выпавших» значений случайной величины. Сделаем много таких экспериментов. Понятно, что каждый раз мы будем получать разное значение суммы. Иными словами, эта сумма является сама по себе случайной величиной со своим каким-то определенным законом распределения. Оказывается, что при достаточно больших закон распределения этой суммы стремится к распределению Гаусса (к слову, характерная ширина «колокола» растет как ). Более подробно читаем в википедии: центральная предельная теорема. В жизни очень часто встречаются величины, которые складываются из большого количества одинаково распределенных независимых случайных величин, поэтому и распределены по Гауссу.

Среднее значение

Среднее значение случайной величины — это то, что мы получим в пределе, если проведем очень много экспериментов, и посчитаем среднее арифметическое выпавших значений. Среднее значение обозначают по-разному: математики любят обозначать через (математическое ожидание или mean value), а заграничные математики через (expectation). Физики же через или . Мы будем обозначать на заграничный лад: .
Например, для Гауссова распределения , среднее значение равно .

Дисперсия

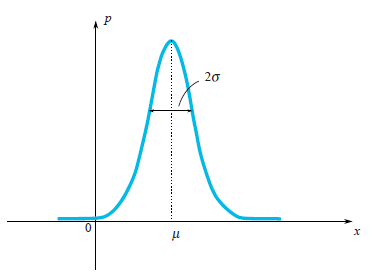
В случае с распределением Гаусса мы совершенно четко видим, что случайная величина предпочитает выпадать в некоторой окрестности своего среднего значения .

Еще раз полюбоваться распределением Гаусса

Как видно из графика, характерный разброс значений порядка . Как же оценить этот разброс значений для произвольной случайной величины, если мы знаем ее распределение. Можно нарисовать график ее плотности вероятности и оценить характерную ширину на глаз. Но мы предпочитаем идти алгебраическим путем. Можно найти среднюю длину (модуль) отклонения от среднего значения: . Эта величина будет хорошей оценкой характерного разброса значений . Но мы с вами очень хорошо знаем, что использовать модули в формулах — одна головная боль, поэтому эту формулу редко используют для оценок характерного разброса.
Более простой способ (простой в смысле расчетов) — найти . Эту величину называют дисперсией, и часто обозначают как . Корень из дисперсии — хорошая оценка разброса случайной величины. Корень из дисперсии еще называют среднеквадратичным отклонением.
Например, для распределение Гаусса можно посчитать, что определенная выше дисперсия в точности равна , а значит среднеквадратичное отклонение равно , что очень хорошо согласуется с нашей геометрической интуицией.
На самом деле тут скрыто маленькое мошенничество. Дело в том, что в определении распределения Гаусса под экспонентой стоит выражение . Эта двойка в знаменателе стоит именно для того, чтобы среднеквадратичное отклонение равнялось бы коэффициенту . То есть сама формула распределения Гаусса написана в виде, специально заточенном для того, что мы будем считать ее среднеквадратичное отклонение.

Независимые случайные величины

Случайные величины бывают зависимыми и нет. Представьте, что вы бросаете иголку на плоскость и записываете координаты ее обоих концов. Эти две координаты зависимы, они связаны условием, что расстояние между ними всегда равно длине иголки, хотя и являются случайными величинами.
Случайные величины независимы, если результат выпадения первой из них совершенно не зависит от результата выпадения второй из них. Если случайные величины и независимы, то среднее значение их произведения равно произведению их средних значений:

Доказательство

Например, иметь голубые глаза и окончить школу с золотой медалью — независимые случайные величины. Если голубоглазых, скажем а золотых медалистов , то голубоглазых медалистов Этот пример подсказывает нам, что если случайные величины и заданы своими плотностями вероятности и , то независимость этих величин выражается в том, что плотность вероятности (первая величина выпала , а вторая ) находится по формуле:

Из этого сразу же следует, что:

Как вы видите, доказательство проведено для случайных величин, которые имеют непрерывный спектр значений и заданы своей плотностью вероятности. В других случаях идея доказательтсва аналогичная.

Фильтр Калмана

Постановка задачи

Обозначим за величину, которую мы будем измерять, а потом фильтровать. Это может быть координата, скорость, ускорение, влажность, степень вони, температура, давление, и т.д.
Начнем с простого примера, который и приведет нас к формулировке общей задачи. Представьте себе, что у нас есть радиоуправляемая машинка, которая может ехать только вперед и назад. Мы, зная вес машины, форму, покрытие дороги и т.д., расcчитали как контролирующий джойстик влияет на скорость движения .



Тогда координата машины будет изменяться по закону:



В реальной же жизни мы не можем учесть в наших расчетах маленькие возмущения, действующие на машину (ветер, ухабы, камушки на дороге), поэтому настоящая скорость машины будет отличаться от расчетной. К правой части написанного уравнения добавится случайная величина :



У нас есть установленный на машинке GPS сенсор, который пытается мерить истинную координату машинки, и, конечно же, не может ее померить точно, а мерит с ошибкой , которая является тоже случайной величиной. В итоге с сенсора мы получаем ошибочные данные:



Задача состоит в том, что, зная неверные показания сенсора , найти хорошее приближение для истинной координаты машины . Это хорошее приближение мы будем обозначать как .
В формулировке же общей задачи, за координату может отвечать все что угодно (температура, влажность...), а член, отвечающий за контроль системы извне мы обозначим за (в примере c машиной ). Уравнения для координаты и показания сенсора будут выглядеть так:

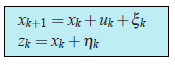    (1)

Давайте подробно обсудим, что нам известно:

• — это известная величина, которая контролирует эволюцию системы. Мы ее знаем из построенной нами физической модели.
  
• Ошибка модели и ошибка сенсора — случайные величины. И их законы распределения не зависят от времени (от номера итерации ).
  
• Средние значения ошибок равны нулю: .
  
• Сам закон распределения случайных величин может быть нам и не известен, но известны их дисперсии и . Заметим, что дисперсии не зависят от , потому что законы распределения не зависят от него.
  
• Предполагается, что все случайные ошибки независимы друг от друга: какая ошибка будет в момент времени совершенно не зависит от ошибки в другой момент времени .
  

Нелишним будет отметить, что задача фильтрации — это не задача сглаживания. Мы не стремимся сглаживать данные с сенсора, мы стремимся получить наиболее близкое значение к реальной координате .

Алгоритм Калмана

Мы будем рассуждать по индукции. Представьте себе, что на -ом шаге мы уже нашли отфильтрованное значение с сенсора , которое хорошо приближает истинную координату системы . Не забываем, что мы знаем уравнение, контролирующее изменение нам неизвестной координаты:



поэтому, еще не получая значение с сенсора, мы можем предположить, что на шаге система эволюционирует согласно этому закону и сенсор покажет что-то близкое к . К сожалению, пока мы не можем сказать ничего более точного. С другой стороны, на шаге у нас на руках будет неточное показание сенсора .
Идея Калмана состоит в том, что чтобы получить наилучшее приближение к истинной координате , мы должны выбрать золотую середину между показанием неточного сенсора и — нашим предсказанием того, что мы ожидали от него увидеть. Показанию сенсора мы дадим вес а на предсказанное значение останется вес :



Коэффициент называют коэффициентом Калмана. Он зависит от шага итерации, поэтому правильнее было бы писать , но пока, чтобы не загромождать формулы расчетах, мы будем опускать его индекс.
Мы должны выбрать коэффициент Калмана таким, чтобы получившееся оптимальное значение координаты было бы наиболее близко к истинной координате . К примеру, если мы знаем, что наш сенсор очень точный, то мы будем больше доверять его показанию и дадим значению больше весу ( близко единице). Eсли же сенсор, наоборот, совсем не точный, тогда больше будем ориентироваться на теоретически предсказанное значение .
В общем случае, чтобы найти точное значение коэффициента Калмана , нужно просто минимизировать ошибку:



Используем уравнения (1) (те которые на голубом фоне в рамочке), чтобы переписать выражение для ошибки:

Доказательство

Теперь самое время обсудить, что означает выражение минимизировать ошибку? Ведь ошибка, как мы видим, сама по себе является случайной величиной и каждый раз принимает разные значения. На самом деле не существует однозначного подхода к определению того, что означает, что ошибка минимальна. Точно как и в случае с дисперсией случайной величины, когда мы пытались оценить характерную ширину ее разброса, так и тут мы выберем самый простой для расчетов критерий. Мы будем минимизировать среднее значение от квадрата ошибки:



Распишем последнее выражение:

ключ к доказательству

Из того что все случайные величины, входящие в выражение для , независимы и средние значения ошибок сенсора и модели равны нулю: , следует, что все «перекрестные» члены равны нулю:
.
Плюс к этому, формулы для дисперсий выглядит намного проще: и (так как )

Это выражение принимает минимальное значение, когда (приравниваем производную к нулю)



Здесь мы уже пишем выражение для коэффициента Калмана с индексом шага , тем самым мы подчеркиваем, что он зависит от шага итерации.
Подставляем в выражение для среднеквадратичной ошибки минимизирующее ее значение коэффициента Калмана . Получаем:

.

Наша задача решена. Мы получили итерационную формулу, для вычисления коэффициента Калмана.

Все формулы в одном месте

Пример

На рекламной картинке в начале статьи отфильтрованы данные с вымышленного GPS сенсора, установленного на вымышленной машине, которая едет равноускоренно c известным вымышленным ускорением .

Еще раз посмотреть на результат фильтрования

Код на матлабе

clear all;
N=100  % number of samples
a=0.1 % acceleration
sigmaPsi=1
sigmaEta=50;
k=1:N
x=k
x(1)=0
z(1)=x(1)+normrnd(0,sigmaEta);
for t=1:(N-1)
  x(t+1)=x(t)+a*t+normrnd(0,sigmaPsi); 
   z(t+1)=x(t+1)+normrnd(0,sigmaEta);
end;
%kalman filter
xOpt(1)=z(1);
eOpt(1)=sigmaEta; % eOpt(t) is a square root of the error dispersion (variance). It's not a random variable. 
for t=1:(N-1)
  eOpt(t+1)=sqrt((sigmaEta^2)*(eOpt(t)^2+sigmaPsi^2)/(sigmaEta^2+eOpt(t)^2+sigmaPsi^2))
  K(t+1)=(eOpt(t+1))^2/sigmaEta^2
 xOpt(t+1)=(xOpt(t)+a*t)*(1-K(t+1))+K(t+1)*z(t+1)
end;
plot(k,xOpt,k,z,k,x)

Анализ

Если проследить, как с шагом итерации изменяется коэффициент Калмана , то можно показать, что он всегда стабилизируется к определенному значению . К примеру, когда среднеквадратичные ошибки сенсора и модели относятся друг к другу как десять к одному, то график коэффициента Калмана в зависимости от шага итерации выглядит так:



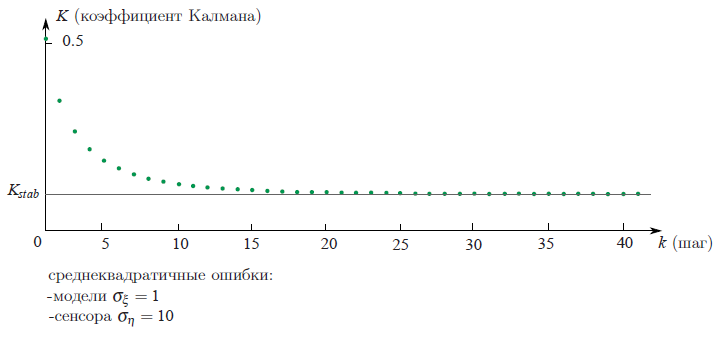
В следующем примере мы обсудим как это поможет существенно облегчить нашу жизнь.

Второй пример

На практике очень часто бывает, что нам вообще ничего не известно о физической модели того, что мы фильтруем. К примеру, вы захотели отфильтровать показания с вашего любимого акселерометра. Вам же заранее неизвестно по какому закону вы намереваетесь крутить акселерометр. Максимум информации, которую вы можете выцепить — это дисперсия ошибки сенсора . В такой непростой ситуации все незнание модели движения можно загнать в случайную величину :



Но, откровенно говоря, такая система уже совершенно не удовлетворяет тем условиям, которые мы налагали на случайную величину , ведь теперь туда запрятана вся неизвестная нам физика движения, и поэтому мы не можем говорить, что в разные моменты времени ошибки модели независимы друг от друга и что их средние значения равны нулю. В этом случае, по большому счету, теория фильтра Калмана не применима. Но, мы не будем обращать внимания на этот факт, а, тупо применим все махину формул, подобрав коэффициенты и на глаз, так чтобы отфильтрованные данные миленько смотрелись.
Но можно пойти по другому, намного более простому пути. Как мы видели выше, коэффициент Калмана с увеличением номера шага всегда стабилизируется к значению . Поэтому вместо того, чтобы подбирать коэффициенты и и находить по сложным формулам коэффициент Калмана , мы можем считать этот коэффициент всегда константой, и подбирать только эту константу. Это допущение почти ничего не испортит. Во-первых, мы уже и так незаконно пользуемся теорией Калмана, а во-вторых коэффициент Калмана быстро стабилизируется к константе. В итоге все очень упростится. Нам вообще никакие формулы из теории Калмана не нужны, нам просто нужно подобрать приемлемое значение и вставить в итерационную формулу:



На следующем графике показаны отфильтрованные двумя разными способами данные с вымышленного сенсора. При условии того, что мы ничего не знаем о физике явления. Первый способ — честный, со всеми формулами из теории Калмана. А второй — упрощенный, без формул.



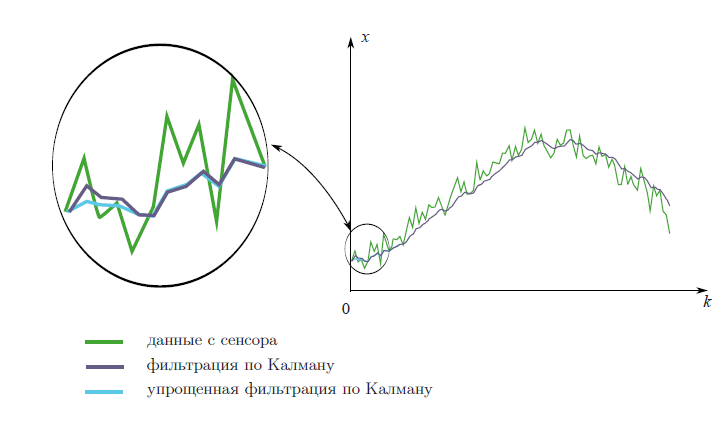
Как мы видим, методы почти ничем не отличаются. Маленькое отличие наблюдается только вначале, когда коэффициент Калмана еще не стабилизировался.

Обсуждение

Как мы увидели, основная идея фильтра Калмана состоит в том, что надо найти коэффициент такой, чтобы отфильтрованное значение



в среднем меньше всего отличалось бы от реального значения координаты . Мы видим, что отфильтрованное значение есть линейная функция от показания сенсора и предыдущего отфильтрованного значения . А предыдущее отфильтрованное значение является, в свою очередь, линейной функцией от показания сенсора и предпредыдущего отфильтрованного значения . И так далее, пока цепь полностью не развернется. То есть отфильтрованное значение зависит от всех предыдущих показаний сенсора линейно:



Поэтому фильтр Калмана называют линейным фильтром.
Можно доказать, что из всех линейных фильтров Калмановский фильтр самый лучший. Самый лучший в том смысле, что средний квадрат ошибки фильтра минимален.

Многомерный случай

Всю теорию фильтра Калмана можно обобщить на многомерный случай. Формулы там выглядят чуть страшнее, но сама идея их вывода такая же, как и в одномерном случае. В этой прекрасной статье вы можете увидеть их: http://habrahabr.ru/post/140274/.
А в этом замечательном видео разобран пример, как их использовать.

Литература

Оригинальную статью Калмана можно скачать вот тут: http://www.cs.unc.edu/~welch/kalman/media/pdf/Kalman1960.pdf.
Этот пост можно прочитать и на английском http://david.wf/kalmanfilter