Введение
Для любого программиста важно знать основы теории алгоритмов, так как именно эта наука изучает общие характеристики алгоритмов и формальные модели их представления. Ещё с уроков информатики нас учат составлять блок-схемы, что, в последствии, помогает при написании более сложных задач, чем в школе. Также не секрет, что практически всегда существует несколько способов решения той или иной задачи: одни предполагают затратить много времени, другие ресурсов, а третьи помогают лишь приближённо найти решение.
Всегда следует искать оптимум в соответствии с поставленной задачей, в частности, при разработке алгоритмов решения класса задач.
Важно также оценивать, как будет вести себя алгоритм при начальных значениях разного объёма и количества, какие ресурсы ему потребуются и сколько времени уйдёт на вывод конечного результата.
Этим занимается раздел теории алгоритмов – теория асимптотического анализа алгоритмов.
Предлагаю в этой статье описать основные критерии оценки и привести пример оценки простейшего алгоритма. На Хабрахабре уже есть статья про методы оценки алгоритмов, но она ориентирована, в основном, на учащихся лицеев. Данную публикацию можно считать углублением той статьи.
Определения
Основным показателем сложности алгоритма является время, необходимое для решения задачи и объём требуемой памяти.
Также при анализе сложности для класса задач определяется некоторое число, характеризующее некоторый объём данных – размер входа.
Итак, можем сделать вывод, что сложность алгоритма – функция размера входа.
Сложность алгоритма может быть различной при одном и том же размере входа, но различных входных данных.
Существуют понятия сложности в худшем, среднем или лучшем случае. Обычно, оценивают сложность в худшем случае.
Временная сложность в худшем случае – функция размера входа, равная максимальному количеству операций, выполненных в ходе работы алгоритма при решении задачи данного размера.
Ёмкостная сложность в худшем случае – функция размера входа, равная максимальному количеству ячеек памяти, к которым было обращение при решении задач данного размера.
Порядок роста сложности алгоритмов
Порядок роста сложности (или аксиоматическая сложность) описывает приблизительное поведение функции сложности алгоритма при большом размере входа. Из этого следует, что при оценке временной сложности нет необходимости рассматривать элементарные операции, достаточно рассматривать шаги алгоритма.
Шаг алгоритма – совокупность последовательно-расположенных элементарных операций, время выполнения которых не зависит от размера входа, то есть ограничена сверху некоторой константой.
Виды асимптотических оценок
O – оценка для худшего случая
Рассмотрим сложность f(n) > 0, функцию того же порядка g(n) > 0, размер входа n > 0.
Если f(n) = O(g(n)) и существуют константы c > 0, n0 > 0, то
0 < f(n) < c*g(n),
для n > n0.
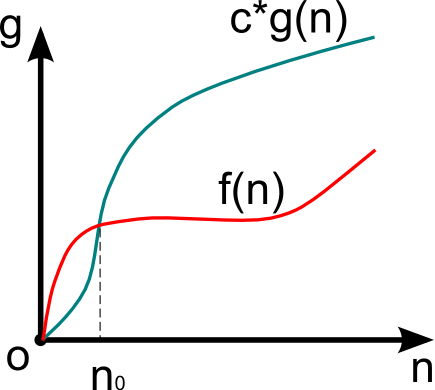
Функция g(n) в данном случае асимптотически-точная оценка f(n). Если f(n) – функция сложности алгоритма, то порядок сложности определяется как f(n) – O(g(n)).
Данное выражение определяет класс функций, которые растут не быстрее, чем g(n) с точностью до константного множителя.
Примеры асимптотических функций
| f(n) | g(n) |
|---|---|
| 2n2 + 7n — 3 | n2 |
| 98n*ln(n) | n*ln(n) |
| 5n + 2 | n |
| 8 | 1 |
Ω – оценка для лучшего случая
Определение схоже с определением оценки для худшего случая, однако
f(n) = Ω(g(n)), если
0 < c*g(n) < f(n)
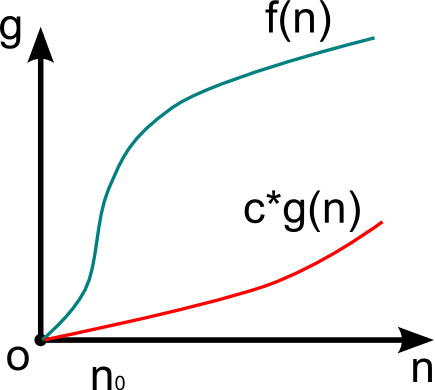
Ω(g(n)) определяет класс функций, которые растут не медленнее, чем функция g(n) с точностью до константного множителя.
Θ – оценка для среднего случая
Стоит лишь упомянуть, что в данном случае функция f(n) при n > n0 всюду находится между c1*g(n) и c2*g(n), где c – константный множитель.
Например, при f(n) = n2 + n; g(n) = n2.
Критерии оценки сложности алгоритмов
Равномерный весовой критерий (РВК) предполагает, что каждый шаг алгоритма выполняется за одну единицу времени, а ячейка памяти за одну единицу объёма (с точностью до константы).
Логарифмический весовой критерий (ЛВК) учитывает размер операнда, который обрабатывается той или иной операцией и значения, хранимого в ячейке памяти.
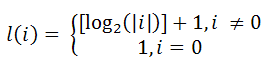
Временная сложность при ЛВК определяется значением l(Op), где Op – величина операнда.
Ёмкостная сложность при ЛВК определяется значением l(M), где M – величина ячейки памяти.
Пример оценки сложности при вычислении факториала
Необходимо проанализировать сложность алгоритма вычисление факториала. Для этого напишем на псевдокоде языка С данную задачу:
void main() {
int result = 1;
int i;
const n = ...;
for (i = 2; i <= n; i++)
result = result * n;
}Временная сложность при равномерном весовом критерии
Достаточно просто определить, что размер входа данной задачи – n.
Количество шагов – (n — 1).
Таким образом, временная сложность при РВК равна O(n).
Временная сложность при логарифмическом весовом критерии
В данном пункте следует выделить операции, которые необходимо оценить. Во-первых, это операции сравнения. Во-вторых, операции изменения переменных (сложение, умножение). Операции присваивания не учитываются, так как предполагается, что она происходят мгновенно.
Итак, в данной задаче выделяется три операции:
1) i <= n
На i-м шаге получится log(n).
Так как шагов (n-1), сложность данной операции составит (n-1)*log(n).
2) i = i + 1
На i-м шаге получится log(i).
Таким образом, получается сумма
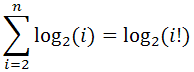 .
.3) result = result * i
На i-м шаге получится log((i-1)!).
Таким образом, получается сумма
 .
.Если сложить все получившиеся значения и отбросить слагаемые, которые заведомо растут медленнее с увел��чением n, получим конечное выражение
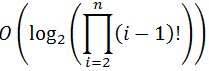 .
.Ёмкостная сложность при равномерном весовом критерии
Здесь всё просто. Необходимо подсчитать количество переменных. Если в задаче используются массивы, за переменную считается каждая ячейка массива.
Так как количество переменных не зависит от размера входа, сложность будет равна O(1).
Ёмкостная сложность при логарифмическом весовом критерии
В данном случае следует учитывать максимальное значение, которое может находиться в ячейке памяти. Если значение не определено (например, при операнде i > 10), то считается, что существует какое-то предельное значение Vmax.
В данной задаче существует переменная, значение которой не превосходит n (i), и переменная, значение которой не превышает n! (result). Таким образом, оценка равна O(log(n!)).
Выводы
Изучение сложности алгоритмов довольно увлекательная задача. На данный момент анализ простейших алгоритмов входит в учебные планы технических специальностей (если быть точным, обобщённого направления «Информатика и вычислительная техника»), занимающихся информатикой и прикладной математикой в сфере IT.
На основе сложности выделяются разные классы задач: P, NP, NPC. Но это уже не проблема теории асимптотического анализа алгоритмов.
