
В настоящее время в Российском сегменте интернета недостаточно освещено современное состояние дел с применением искусственного интеллекта (ИИ) в робототехнике. Желание исправить эту ситуацию побудило опубликовать материал связанный с технологиями разработки интеллектуальных систем управления. В работе рассматривается историческое развитие средств искусственного интеллекта (нечеткая логика (НЛ), генетические алгоритмы (ГА), нечеткие нейронные сети (ННС)) для проектирования системы автоматического управления (САУ). Сравнение методологий проектирования проводится на примере робота, основанного на платформе Arduino.
Введение
В настоящий момент разработка, развитие и реализация эффективных высоких наукоемких информационных технологий (ИТ) (создаваемых в различных областях науки и техники) неразрывно связаны с необходимостью разработки и повышения уровня интеллектуальности используемых процессов и систем управления, объективно учитывающие в законах управления контекстуально-зависимые физические эффекты, ограничения и информационные границы, реально существующие в конкретных моделях объекта управления (ОУ).
В теории и проектировании систем управления в настоящее время большое внимание уделяется выявлению роли и эффективному применению робастных интеллектуальных систем управления (ИСУ) в интенсивном развитии и качественном совершенствовании современных высоких ИТ интеллектуального управления сложными физическими ОУ.
Сложность описания физических систем, в свою очередь, приводит к необходимости аппроксимации моделей ОУ и применению приближенных решений, которые не гарантируют необходимые и достаточные условия достижения цели управления в непредвиденных ситуациях и информационного риска. Поэтому в теории и систем управления одним из эффективных подходов снижения риска принятия решения (от неполноты описания модели ОУ) является разработка структур робастных ИСУ [1].
Эволюция интеллектуальный систем управления
Задачи управления существенно нелинейными и глобально неустойчивыми ОУ исследовались при наличии различных типов стохастического возмущения на ОУ. С помощью разработанной системы стохастического моделирования, определялись предельные возможности классических САУ основанных на использовании исполнительного устройства САУ в виде традиционного ПИД-регулятора (см. Таблицу 1, позиция 1). В результате проведенного исследования был установлен следующий факт: классические САУ, основанные на ПИД-регуляторе с постоянными коэффициентами усиления, часто не справляются с задачей управления в случае глобально неустойчивых и существенно нелинейных ОУ, находящихся под воздействием негауссовского (например, Рэлеевского) стохастического шума, а также в условиях временных задержек в каналах измерения.
Этот факт объясняется следующими обстоятельствами. Классические САУ основаны на принципе глобальной отрицательной обратной связи и методе компенсации ошибки управления. Однако, в сложных ОУ (пример с Arduino-роботом ниже) недостаточно иметь результат оптимизации только по одному критерию качества управления, типа минимума ошибки управления. Поэтому на практике при проектировании ИСУ сложными ОУ возникает следующая проблема: как ввести в систему управления другие, дополнительные критерии качества управления?
Таблица 1. Эволюция ИСУ

К таким критериям относятся, например минимум производства энтропии в ОУ, и/или минимум производства энтропии в самой системе управления (учитывающие тепловые потери, потери полезной работы в объекте и системе управления), или другие более сложные, векторные критерии качества управления.
Примечание. Подобные и смежные вопросы построения физической теории управления рассматривались в работах А.А. Красовского, С.В. Емельянова, Ю.И. Самойленко, А.Г. Бутковского, Л.И. Розоноэра, Р. Поплавского, А.М. Цирлина А.П. Фрадкова и мн. др.
Разрешить этот вопрос с помощью процесса проектирования стандартного ПИД-регулятора с постоянными коэффициентами усиления практически невозможно. Ограниченные возможности по реализации сложных критериев качества управления в классических САУ, особенно в указанных выше случаях управления, послужили отправной точкой к развитию ИСУ, основанных на идеях близких к использованию стратегий управления, используемых человеком-экспертом в сложных ситуациях.
Для моделирования «человеко-машинных» стратегий управления на первом этапе стали использоваться так называемые «мягкие вычисления», в основе которых лежит теория нечетких множеств и нечеткого вывода. Так, например, представленная в таблице 1-1 структура преобразуется в экспертную систему управления Таблица 1-2 последовательным наращиванием составляющих блоков в классической структуре САУ (в данном случае введением блока нечеткого вывода) и является примером первого поколения ИСУ (рис.1).
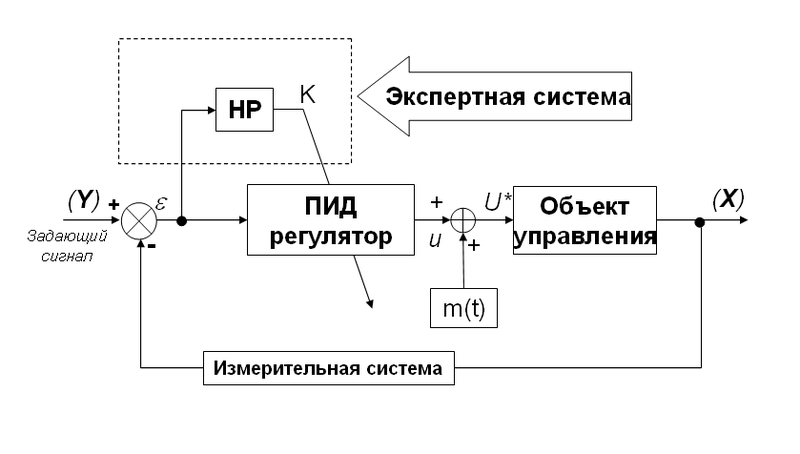
Рис. 1. Система управления с нечетким регулятором
Таким образом, первое поколение ИСУ представляло собой нечеткие экспертные системы (ЭС). Основную роль в этих ЭС играло качество базы знаний (БЗ), которое определялось опытом и субъективными знаниями человека-эксперта. Однако, в случае управления глобально неустойчивыми и существенно нелинейными ОУ, находящимися под воздействием сложных стохастических шумов, даже опытному человеку-эксперту трудно подобрать оптимальную (с точки зрения качества управления) БЗ НР. Эта проблема — узкое место всех первых (и их последующих модификаций) ИСУ. Поэтому, использование ЭС в качестве инструментария извлечения знаний и формирования БЗ (как основы технологии проектирования ИСУ) не привело к ожидаемому существенному успеху (хотя существует много примеров промышленного внедрения) в силу сложности ОУ и субъективности информации, вносимой экспертом.
С точки зрения технологии проектирования основной проблемой внедрения ИСУ первого поколения являлась их слабая адаптивность к изменениям параметров ОУ (вызванных, например, старением структуры ОУ или резким изменением внешней среды), а также низкая робастность полученных законов управления. Для решения подобных проблем были разработаны ИСУ второго поколения, используя технологии мягких вычислений, объединяющие в единую цепочку ГА, ННС и нечеткий регулятор (НР). Это позволило исключить субъективное мнение эксперта на этапе формирования структуры и параметров БЗ НР. В свою очередь развитие ИСУ, основанных на мягких вычислениях, породило несколько подходов к формированию структур БЗ. Первоначально планировалось формировать некоторый достаточно огрубленный обучающий сигнал (ОС) от ГА, и извлекать БЗ путем аппроксимации полученного ОС на ННС. Структура ИСУ второго поколения представлена путем введения в структуру ИСУ первого поколения блока, включающего в себя ГА и ННС (см., Таблицу 1 — 3).
В дальнейшем второе поколение ИСУ стало использовать новый вид обратной связи, называемой интеллектуальной глобальной обратной связью (ИГОС), представленной в Таблице 1, (позиция 4). Её использование дает возможность извлекать объективные знания непосредственно из самого динамического поведения ОУ и исполнительного устройства САУ. Контур ИГОС включает ГА для получения информации об оптимальном сигнале управления (исходя из динамического и термодинамического поведения самого ОУ и ПИД-регулятора) и ННС, аппроксимирующей данный оптимальный сигнал управления с помощью заданной структуры нейронной сети. Основным блоком в структуре ИСУ этого поколения является система моделирования оптимального сигнала управления (СМОСУ) с помощью ГА и критерия качества управления, заданного в виде одной из составляющих вектор-функции пригодности ГА (рис.2).
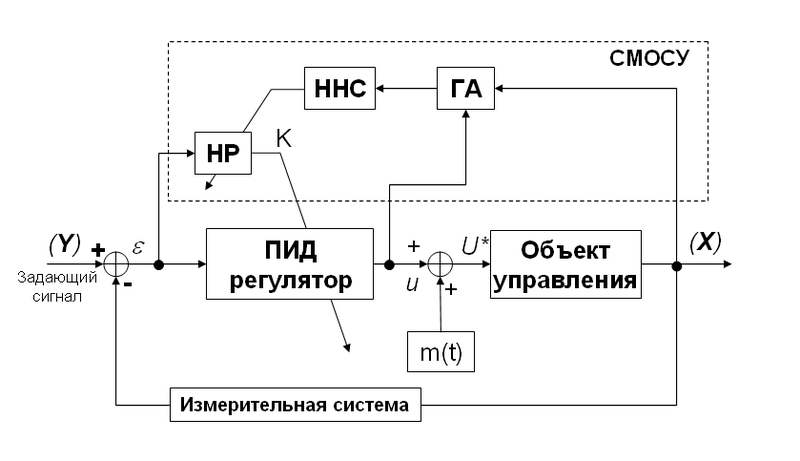
Рис. 2. Интеллектуальная система управления второго поколения
Основной проблемой, решаемой ИСУ пятого поколения с ИГОС, является наличие возможности достижения требуемого уровня робастности на заданном классе как параметрических, так и внешних случайных возмущений различной вероятностной природы (с различными функциями плотности распределения вероятностей). Другой важной проблемой является определение требуемого соотношения между точностью описания (аппроксимации) ОС и необходимым уровнем робастности всей структуры ННС. Обе указанные проблемы решаются на втором этапе технологии построения БЗ ИСУ с помощью программных средств инструментария, названного «Оптимизатор Баз Знаний» (ОБЗ) (рис.3).
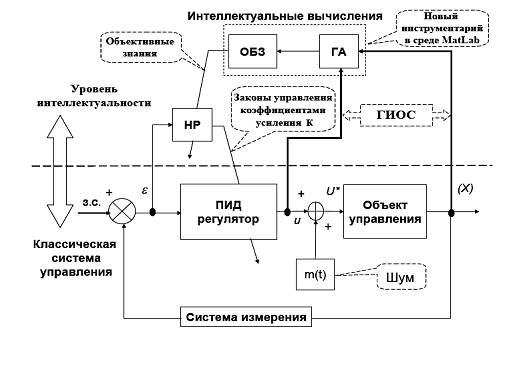
Рис. 3. Интеллектуальная система управления пятого поколения. С программным инструментарием ОБЗ
Подробнее ознакомится с методикой проектирования ИСУ можно на примерах проектирования подобных систем:
Интеллектуальное управление манипулятором
Метод извлечения знаний из физически измеряемого сигнала
Удаленная настройка БЗ
Рассмотрим пример применения ИСАУ.
Математическая модель и Робот
Управление объектом типа «Каретка — перевернутый маятник» (рис.4) является одной из типовых задач в теории управления, т.к. решение этой задачи наглядно демонстрирует качество САУ. Рассмотрим динамику модели в виде одноосевой каретки с перевёрнутым маятником, закреплённым на оси:
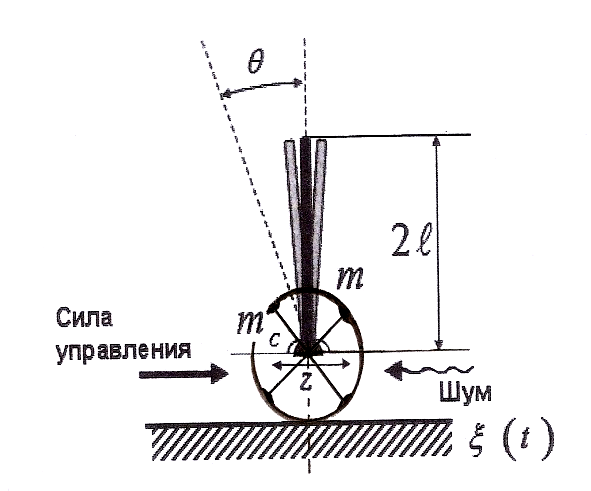
Рис.4 Модель системы «Каретка- перевернутый маятник»
Динамика этого ОУ описывается системой дифференциальных уравнений второго порядка, выводимых, с учетом сил трения и упругости каретки, из баланса моментов и проекций сил на горизонтальную ось Z:
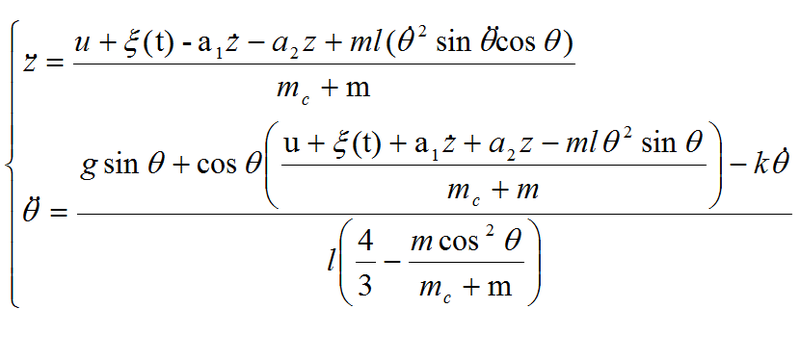
Уравнения для скорости производства энтропии следующие:
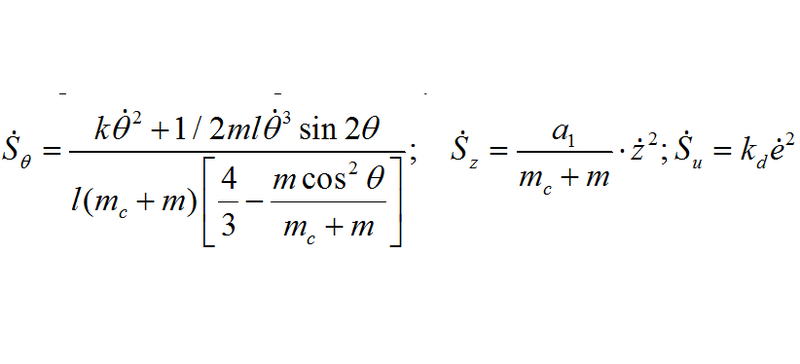
В уравнениях z и «тета» — обобщенные координаты; g — ускорение свободного падения, мс — масса тележки, m — перевернутого маятника (называемого «шест»), l — половина длины маятник, k и а1 коэффициенты трения в z и «тета» соответственно, а2 — сила упругости тележки, «кси» внешний стохастический шум, а u — сила управления.
Динамическая система обладает глобальной динамической неустойчивостью, при отсутствии управляющей силы происходит неограниченный рост угла отклонения, т.е. маятник падает. Задача управления системой состоит в том, чтобы воздействуя с помощью силы управления на тележку, удерживать (стабилизировать) маятник в вертикальном положении (угол отклонения оси маятника от вертикали к 0) в условиях изменения среды функционирования.
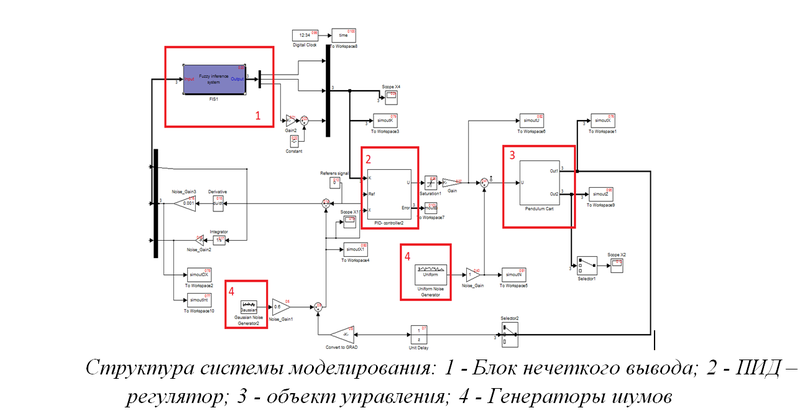
Рис.5. Математическая модель реализованная в среде Matlab Simulink
Модель (рис.5) включает в себя ПИД — регулятор, шумы в системе управления и измерения, а также блок, формирующий сигнал для регулятора.
Данная компьютерная модели используется для получения обучающего сигнала и настройки БЗ с использованием ОБЗ. Основные этапы построения БЗ с использованием ОБЗ рассмотрены в [1,9].
Данный тип ОУ является типовым (benchmark) для тестирования программного инструментария робастного интеллектуального управления. Примеры подобных систем рассмотрены в работах [2 – 8] и представлены на рис. 6.

Рис. 6. Аналогичные ОУ
Рассмотрим устройство подобного макета ОУ. На рис. 7 представлен макет используемый для тестирования технологий проектирования ИСАУ с использованием ОБЗ. Подробно данный тип роботов рассмотрен тут.

Рис. 7. Макет системы
В качестве измерительной системы (рис. 7, Sensor) в макете используется плата с комбинацией датчиков — гироскопа и акселерометра — 5 DoF (пять степеней свободы) IDG500/ADXL335. Ядром и центральным элементам системы является микроконтроллер компании Arduino основанный на процессоре ATmega328. Плата оборудована USB разъемом, для передачи данных с процессора на компьютер. Интерфейс USB используется при проведении экспериментов для передачи и приема данных (угла отклонения и величины управляющего воздействия), а также для удаленной настройки, речь о которой пойдет ниже. Подключение датчиков осуществляется с использованием аналоговых входов микроконтроллера.
Базовые функции программ макета представлены на рис. 8., обобщённо их можно записать в псевдокод:
• Измерение
• Фильтрация
• Управление
• Подсчет времени (задержка).
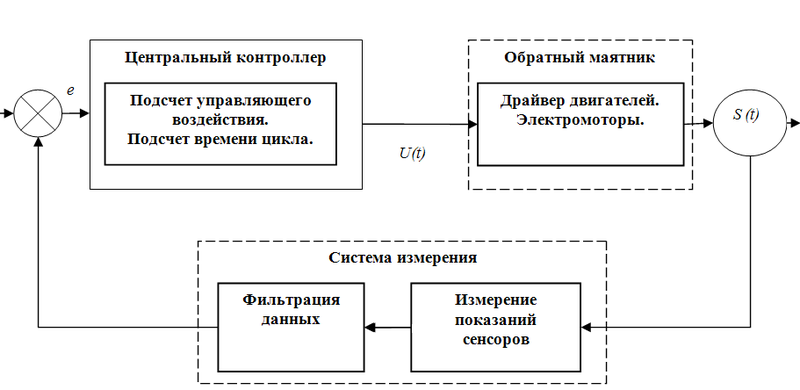
Рис. 8. Псевдокод алгоритма работы робота
Отметим, что алгоритм работы макета системы, представленный на рис. 8, является частным примером САУ с обратной связью, рассмотренной ранее (таблица 1-1).
Эксперимент
Для проверки робастности контроллеров мы используем две ситуации управления:
1) Типовую ситуацию — для которой разрабатывать регуляторы (ситуация описанная в ОС и мат. модели)
2) Непредвиденную ситуацию 1 — дополнительный шум в системе (в эксперименте использовалась крупа)
3) Непредвиденную ситуацию 2 — задержка управляющего воздействия увеличена в три раза.
В видео демонстрируются три типа регуляторов:
1) Классический ПИД — регулятор
2) Нечеткий регулятор на основе ОБЗ
3) Квантовый регулятор, основанный на новых типах вычислений с использованием скрытой квантовой информацией (описание квантового регулятора и технологии проектирования подобной ИСУ здесь и здесь).
Выводы
Структура данной технологии проектирования нечетких регуляторов и ИСУ должна включать в себя:
o многокритериальный ГА для поиска оптимального управления и верификации математических моделей,
o нечеткую нейронную сеть для аппроксимации найденного с помощью ГА оптимального сигнала управления и извлечение на его основе «оптимальной» БЗ,
o «тонкую» настройку БЗ на основе ГА с использованием информационно-энтропийных критериев.
ОБЗ позволяет осуществить принцип проектирования оптимальной ИСУ с максимальным уровнем надежности и управляемости сложным ОУ в условиях неопределенности исходной информации.
Применение БЗ, спроектированных с помощью ОБЗ, в структуре ИСУ расширяет область промышленных приложений САУ к сложным динамическим ОУ.
Ссылки
1. Ульянов С.В., Литвинцева Л.В., Добрынин В.Н., Мишин А.А. Интеллектуальное робастное управление: технологии мягких вычислений, М.: ВНИИгеосистем, 2011.
2. Grasser, F., D’Arrigo, A., Colombi, S. and Rufer, A. Joe: A mobile inverted pendulum. // IEEE Transaction Electronics. – 2002. – Vol. 49. – No 1. – pp. 107 – 114.
3. Choi D., Oh J.-H. Human-friendly motion control of a wheeled inverted pendulum by reduced-order disturbance observer // IEEE International Conference on Robotics and Automation Pasadena, CA, USA, May 19-23, 2008. – pp. 2521 – 2526.
4. Nawawi S. W., Ahmad M. N. and Osman J. H. S., Real-time control system for a two-wheeled inverted pendulum mobile — robot, // Advanced Knowledge Application in Practice / I. Fuerstner (Ed). — InTech. – 2010. – pp. 299 – 312.
5. Gocmen A. Design of two wheeled electric vehicle. – Master Sci. Thesis. – Atilim University, Temmuz. – 2011.
6. Takeneka T., Hirano M., Izumi H., Kuwabara K., Koyama K., Kobashi Sh. Inverted pendulum mobile vehicle. – Patent US 8,224,891 B2. – Date of Patent. – Jul. 24, 2012.
7. Castro A. Modeling and dynamic analysis of a two-wheeled inverted pendulum. – Master Science Thesis. – Georgia Institute of Technology, Atlanta, USA. – 2012.
8. Nasir A., Ahmad N., Ghazali R., Pakheri N. Performance comparison between fuzzy logic controller (FLC) and PID controller for a highly nonlinear two-wheels balancing robot // 1st International Conference on Informatics and Computational Intelligence. – IEEE Computer Society. – 2011. – pp. 176 – 181.
9. Решетников А.Г., Ульянов С. В., Метод извлечения знаний из физически измеряемого сигнала обучения: проектирование баз знаний нечеткого регулятора, «Системный анализ в науки и образовании» Эл № ФС77-51141 от 14.09.2012г. Выпуск №1, 2013