Алгоритм нечёткой кластеризации fuzzy c-means на PHP

Доброго времени суток.

Пост и код приведённый ниже, предназначен не столько для использования алгоритма в рабочих целях, сколько для того, чтобы понять, как алгоритм fuzzy c-means работает и возможно, дать толчок к реализации этого алгоритма на других языках либо для усовершенствования приведённого кода и его дальнейшего использования в рабочих целях.

Общие сведения

Для начала стоит очень быстро рассказать, что такое кластеризация и что особенного в нечёткой кластеризации.

Кластеризация, как описывает это слово Викисловарь,

группировка, разбиение множества объектов на непересекающиеся подмножества, кластеры, состоящие из схожих объектов

Данное определение вполне понятное и я думаю не нуждается в дополнительном объяснении.

Что же тогда такое «нечёткая кластеризация»?
Нечёткую кластеризацию от просто кластеризации отличает то, что объекты, которые подвергаются кластеризации, относятся к конкретному кластеру с некой принадлежностью, а не однозначно, как это бывает при обычной кластеризации. Например, при нечёткой кластеризации объект A относится к кластеру K1 с принадлежностью 0.9, к кластеру K2 — с принадлежностью 0.04 и к кластеру К3 — с принадлежностью 0.06. При обычной же (чёткой) кластеризации объект А был бы отнесён к кластеру K1.

Математическое описание данного алгоритма Вы можете найти в данном хабрапосте.

Реализация fuzzy c-means на PHP.

Давайте перейдём непосредственно к реализации алгоритма. Для этого я бы рассмотрел реализацию на более-менее реальном примере. Таким примером может быть следующий — давайте кластеризируем пиксели по их RGB-значению, т.е. фактически по цвету. В итоге, мы сможем увидеть результат выполнения алгоритма наглядно.

Ниже приведён код алгоритма, который далее я разберу чуть подробнее.

Реализация алгоритма fuzzy c-means для кластеризации точек по их RGB-значению

define('EPLSION', 0.1);
define('MAX_EXECUTION_CYCLES', 150);
define('POINTS_COUNT', 100);
define('CLUSTERS_NUM', 3);
define('FUZZ', 1.5);

class Point
{
  public $r;
  public $g;
  public $b;
}

// Random values 0 - 1
function random_float ($min,$max) {
   return ($min+lcg_value()*(abs($max-$min)));
}
 
 
//  Fuzzy C Means Algorithm
function distributeOverMatrixU($arr, $m, &$centers)
{
    $centers = generateRandomPoints(CLUSTERS_NUM);
    $MatrixU = fillUMatrix(count($arr), count($centers));
     
    $previousDecisionValue = 0;
    $currentDecisionValue = 1;

    for($a = 0; $a < MAX_EXECUTION_CYCLES && (abs($previousDecisionValue - $currentDecisionValue) > EPLSION); $a++){
        $previousDecisionValue = $currentDecisionValue;
        $centers = calculateCenters($MatrixU, $m, $arr);

        foreach($MatrixU as $key=>&$uRow){
            foreach($uRow as $clusterIndex=>&$u){
                $distance = evklidDistance3D($arr[$key], $centers[$clusterIndex]);
                $u = prepareU($distance, $m);
            }

            $uRow = normalizeUMatrixRow($uRow);
        }
        $currentDecisionValue = calculateDecisionFunction($arr, $centers, $MatrixU);
    }
 
    return $MatrixU;
}

function fillUMatrix($pointsCount, $clustersCount)
{
    $MatrixU = array();
    for($i=0; $i<$pointsCount; $i++){
        $MatrixU[$i] = array();
        for($j=0; $j<$clustersCount; $j++){
            $MatrixU[$i][$j] = random_float(0, 1);
        }
        $MatrixU[$i] = normalizeUMatrixRow($MatrixU[$i]);
    }

    return $MatrixU;
}

function calculateCenters($MatrixU, $m, $points)
{
    $MatrixCentroids = array();

    for($clusterIndex=0; $clusterIndex < CLUSTERS_NUM; $clusterIndex++){
        $tempAr = 0;
        $tempBr = 0;
        $tempAg = 0;
        $tempBg = 0;
        $tempAb = 0;
        $tempBb = 0;

        foreach($MatrixU as $key=>$uRow){
            $tempAr += pow($uRow[$clusterIndex],$m);
            $tempBr += pow($uRow[$clusterIndex],$m) * $points[$key]->r;

            $tempAg += pow($uRow[$clusterIndex],$m);
            $tempBg += pow($uRow[$clusterIndex],$m) * $points[$key]->g;

            $tempAb += pow($uRow[$clusterIndex],$m);
            $tempBb += pow($uRow[$clusterIndex],$m) * $points[$key]->b;
        }

        $MatrixCentroids[$clusterIndex] = new Point();
        $MatrixCentroids[$clusterIndex]->r = $tempBr / $tempAr;
        $MatrixCentroids[$clusterIndex]->g = $tempBg / $tempAg;
        $MatrixCentroids[$clusterIndex]->b = $tempBb / $tempAb;
    }

    return $MatrixCentroids;
}

function calculateDecisionFunction($MatrixPointX, $MatrixCentroids, $MatrixU)
{
    $sum = 0;
    foreach($MatrixU as $index=>$uRow){
        foreach($uRow as $clusterIndex=>$u){
            $sum += $u * evklidDistance3D($MatrixCentroids[$clusterIndex], $MatrixPointX[$index]);
        }
    }

    return $sum;
}

function evklidDistance3D($pointA, $pointB)
{
    $distance1 = pow(($pointA->r - $pointB->r),2);
    $distance2 = pow(($pointA->g - $pointB->g),2);
    $distance3 = pow(($pointA->b - $pointB->b),2);
    $distance = $distance1 + $distance2 + $distance3;
    return sqrt($distance);
}

function normalizeUMatrixRow($MatrixURow)
{
    $sum = 0;
    foreach($MatrixURow as $u){
        $sum += $u;
    }

    foreach($MatrixURow as &$u){
        $u = $u/$sum;
    }

    return $MatrixURow;
}

function prepareU($distance, $m)
{
    return pow(1/$distance , 2/($m-1));
}


function generateRandomPoints($count){
    $points = array_fill(0, $count, false);
    array_walk($points, function(&$value, $key){
        $value = new Point();
        $value->r = rand(20, 235);
        $value->g = rand(20, 235);
        $value->b = rand(20, 235);
    });

    return $points;
}


$points = generateRandomPoints(POINTS_COUNT);
$centers = array();

$matrixU = distributeOverMatrixU($points, FUZZ, $centers);

Начнём рассмотрение алгоритма с функции, которая собственно и запускает сам алгоритм кластеризации — distributeOverMatrixU
Входными параметрами для неё являются массив кластеризируемых объектов(в нашем случае рандомно заполненный массив, содержащий об]екты класса Point) и коэффициент неопределённости. Возвращаемое значение — матрица принадлежности. Также был добавлен в функцию in/out параметр centers, в котором после выполнения алгоритма будут центры наших кластеров.

Шаги по нахождению новых центров кластеров и пересчёте матрицы принадлежности ограничены константами MAX_EXECUTION_CYCLES и EPSILON, где MAX_EXECUTION_CYCLES — ограничивает количество шагов, EPSILON — ограничивает точность нахождения матрицы принадлежности.

Каждый шаг алгоритма таков:
1) рассчитываем центры кластеров с помощью функции calculateCenters
2) далее для каждого объекта рассчитываем Евклидово расстояние до центра каждого кластера (функция evklidDistance3D — пространство 3х мерное у нас)
3) рассчитываем коэффициент принадлежности u для данного объекта (функция prepareU)
4) нормализуем коэффициенты u для данного объекта (функция normalizeUMatrixRow)
5) рассчитываем значение решающей функции (функция calculateDecisionFunction)
6) далее сравнивается текущее значение решающей функции с предыдущим её значением и если их разница меньше установленного EPSILON, то алгоритм прекращает работу.

Теперь чуть подробнее о каждом шаге:
1) центры рассчитываются по следующей формуле

где wk(x) — коэффициент принадлежности, m — коэффициент неопределённости, x — объект (в самом алгоритме в качестве х выступают составляющие R, G, B)

2) Евклидово расстояние мы рассчитываем для 3х измерений, т.е. формула следующая:
r = sqrt((r2-r1)^2 + (g2-g1)^2 + (b2-b1)^2);
где r,g,b — составляющие RGB

3) коэффициент принадлежности рассчитывается по формуле
u = (1/d)^(2/(m-1)),
где d — расстояние от объекта до центра кластера, m — коэффициент неопределённости.

4) нормализация всех коэффициентов принадлежности объекта — преобразуем коэффициенты, чтобы в сумме они давали 1, т.е. фактически делим каждый коэффициент на сумму всех коэффициентов данного объекта

5) решающая функция возвращает сумму всех Евклидовых расстояний каждого объекта к каждому центру кластера умноженному на коэффициент принадлежности

6) по модулю вычитаем предыдущее и текущее значение решающей функции, и если это разница меньше EPSILON — алгоритм прекращает и возвращается найденная матрица принадлежности.

В конце хотелось бы добавить пару скриншотов, демонстрирующих результаты работы алгоритма.
На рисунках видно, что алгоритм отработал верно и отнём похожие по цветам точки к одним и тем же класстерам

Демонстрация работы алгоритма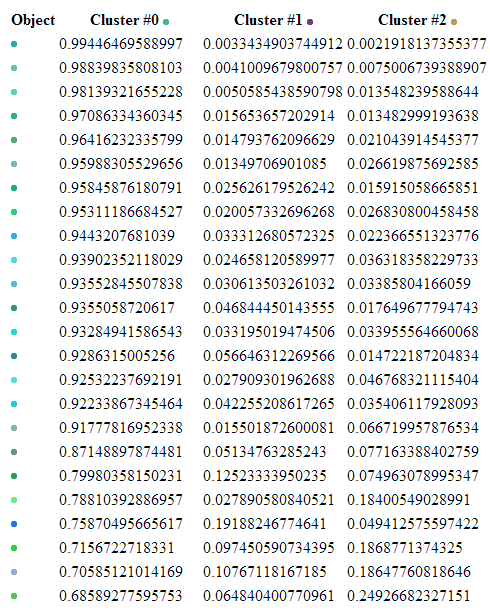

Таким образом, я представил Вам базовую реализацию алгоритма нечёткой кластеризации fuzzy c-means. Надеюсь, она будет Вам полезна.
Спасибо за внимание.