В конце 2013 г. Технический комитет по стандартизации «Криптографическая защита информации» (ТК 26), Академия криптографии Российской Федерации и ОАО «ИнфоТеКС» объявили о проведении конкурса по криптоанализу отечественного стандарта хэширования ГОСТ Р 34.11-2012. Подробное описание условий конкурса опубликовано на сайте www.streebog.info. Таким образом, можно считать, что существующие работы по анализу данного криптостандарта стали предметом повышенного интереса криптоаналитиков, поскольку они являются отправной точкой для дальнейших исследований алгоритма ГОСТ Р 34.11-2012.
На текущий момент известно несколько работ, посвященных криптоанализу ГОСТ Р 34.11-2012. Но именно в работе Zongyue Wang, Hongbo Yu и Xiaoyun Wang «Cryptanalysis of GOST R Hash Function» предложены наиболее эффективные атаки на данный алгоритм. Поэтому, на мой взгляд, именно эта работа представляет наибольший интерес среди работ по данной теме; ее перевод я и предлагаю вашему вниманию.
В переводе сохранены авторские названия стандартов хэширования: под названием «ГОСТ» имеется в виду стандарт 1994 года ГОСТ Р 34.11-94, а «ГОСТ Р» обозначает исследуемый в работе алгоритм ГОСТ Р 34.11-2012.
Работа переведена и публикуется на русском языке с разрешения ее авторов.
ГОСТ Р – это стандарт на хэш-функцию в России. Данная работа представляет некоторые результаты криптоанализа ГОСТ Р. Используя приемы rebound-атак, мы получили атаки, позволяющие найти коллизии функции сжатия с уменьшенным количеством раундов. Предложена атака на 9,5 раунда с трудоемкостью 2176 операций и требованиями к памяти 2128 байт. На основе данной атаки предложен различитель (Прим. перев.: различитель – алгоритм, позволяющий отличить атакуемую функцию от случайно и равновероятно выбранной функции). Более того, представлен метод конструирования k-коллизий для 512-битной версии ГОСТ Р, который показывает слабость структуры, использованной в ГОСТ Р. Насколько нам известно, это первые результаты по анализу ГОСТ Р.
Ключевые слова: хэш-функция, ГОСТ Р, rebound-атака, мультиколлизия.
Хэш-функции играют важную роль в криптографии и используются во многих приложениях, например, электронной подписи, аутентификации и обеспечения целостности данных. С момента взлома алгоритмов MD5 и SHA-1 [1, 2] криптографы находятся в поиске стойких и эффективных хэш-функций. Преемник алгоритма ГОСТ, ГОСТ Р является стандартом хэширования в России [3]. Похожий по своей структуре на Whirlpool [4], он также использует подобный AES блочный шифр в своей функции сжатия.
Rebound-атака – это технология использования степеней свободы, которая может быть применена для поиска коллизий для алгоритмов хэширования, основанных как на перестановках, так и на блочных шифрах. Данная технология была впервые предложена в работе Менделя (Mendel) и др. для формирования атак по поиску коллизий для усеченных алгоритмов Whirlpool и Grøstl [5]. Она нацелена на эффективный поиск пар значений, которые соответствуют предопределенному усеченному дифференциалу. Процедура поиска разделяется на две фазы: внутренняя (inbound) фаза и внешняя (outbound) фаза. Во внутренней фазе атакующий полностью использует доступные степени свободы и генерирует достаточно много пар значений, удовлетворяющих пути усеченного дифференциала внутренней фазы, используемых в качестве точек старта. Впоследствии, во внешней фазе данные точки старта проверяются с целью поиска пар значений, удовлетворяющих пути усеченного дифференциала внешней фазы.
Ламберже (Lamberger) и др. усилили данную технологию в [6] и получили улучшенные результаты для Whirlpool. Доступные степени свободы в ключевой схеме используются для расширения внутренней фазы rebound-атаки на величину до двух раундов. Лучшие результаты работы [6] – это почти-коллизия (near-collision) для 9,5 раунда функции сжатия с трудоемкостью 2176. Данный результат затем использовался для построения первого алгоритма различения для полной 10-раундовой функции сжатия алгоритма Whirlpool. В то же самое время Жильбер (Gilbert) и др. предложили технологию расширенной замены (Super-Sbox) для rebound-атаки в [7], где два раунда AES-подобных преобразований рассматривались как один уровень расширенной замены. Кроме того, rebound-атака может также быть применена для анализа AES и AES-подобных блочных шифров [8, 9], а равно и ARX-шифров (Прим. перев.: ARX – аббревиатура от Add-Rotate-Xor, данные операции являются основными в ARX-шифрах). [10]. Недавно, с использованием адаптированной технологии rebound-атаки, Дюк (Duc) и др. сконструировали дифференциальные характеристики для Keccak в [11].
В качестве альтернативы поиску коллизий для хэш-функций, Жуа (Joux) предложил метод конструирования мультиколлизий в [12]. Он показал, что для итеративной хэш-функции поиск мультиколлизии вовсе не сложнее поиска одиночной коллизии. Этот метод может быть применим в большинстве случаев для анализа стойкости структуры хэш-функции.
Ввиду схожести структуры ГОСТ Р и Whirlpool, rebound-атака, использованная в [6] для анализа Whirlpool, может быть также применима к ГОСТ Р. Однако, ГОСТ Р использует матричную перестановку вместо операции ShiftRows в AES-подобных структурах. Мы покажем, что эта разница приводит к большей уязвимости.
В данной работе мы представляем первые результаты анализа ГОСТ Р. Более точно, применив методы rebound-атаки, схожие с приведенными в [6], мы получили атаки по поиску коллизии для 4,5, 5,5, 7,5 и 9,5 раунда функции сжатия ГОСТ Р. Наши атаки по поиску коллизий для функции сжатия ГОСТ Р приведены в табл. 1. Далее мы показали, что атака на 9,5 раунда может быть впоследствии сконвертирована в 10-раундовый различитель. Кроме того, мы предложили метод конструирования мультиколлизий для полной 512-битной версии ГОСТ Р. Этот результат показывает, что структура, использованная в ГОСТ Р, не является идеальной.
Табл. 1. Сводные результаты для функции сжатия ГОСТ Р. Ресурсоемкость, указанная в скобках, относится к модифицированным атакам, использующим предвычисляемую таблицу, для заполнения которой требуется 2128 единиц времени и памяти.
Краткое содержание данной работы: в главе 2 мы кратко опишем хэш-функцию ГОСТ Р. Затем мы приведем подробное описание rebound-атаки в главе 3; описание различителя будет дано в главе 4. В главе 5 мы представим метод конструирования мультиколлизий. Наконец, в главе 6 мы подведем итоги работы.
ГОСТ Р – это стандарт хэширования в России [3]. Он обрабатывает блоки сообщений размером 512 бит и вычисляет 512- или 256-битные хэш-значения. l-битное сообщение сначала дополняется до размера, кратного 512 битам. Единичный бит присоединяется к концу сообщения; после него следуют 512 - 1 - (l mod 512) нулевых бит. Пусть M = Mt || Mt-1 ||…|| M1 – это сообщение, состоящее из t блоков после дополнения, представленное в big-endian форме. Тогда, как показано на рис. 1, вычисление H(M) можно описать следующим образом:

Рис. 1. Хэш-функция ГОСТ Р

где IV – предопределенное начальное значение, а обозначает операцию сложения в кольце
обозначает операцию сложения в кольце  . gN(h, m) – это функция сжатия алгоритма ГОСТ Р, которая основана на 512-битном блочном шифре и вычисляется так:
. gN(h, m) – это функция сжатия алгоритма ГОСТ Р, которая основана на 512-битном блочном шифре и вычисляется так:

Используемый в ГОСТ Р блочный шифр E представляет собой вариант AES, который обновляет 64-байтное состояние (представленное как массив 8 x 8 – состояние можно представить также как 64 x 64 в поле GF(2)) и раундовый ключ, выполняя 12 раундов. В каждом раунде состояние обновляется выполнением раундового преобразования ri следующим образом:

Раундовое преобразование состоит из:
Раундовый ключ ki вычисляется так:

где Ci – константы алгоритма ГОСТ Р, а начальное значение k1 определяется как
После последнего раунда преобразования, обновляющего состояние, выходное значение блочного шифра E, предыдущее значение состояния hj-1 и блок сообщения Mj объединяются операцией XOR в качестве выходного значения функции сжатия.
Мы обозначим результат раундового преобразования ri как Ri+1, а промежуточные состояния после преобразований S, P и L как, соответственно, RiS, RiP и RiL. Начальное состояние .
.
Rebound-атака – это технология анализа хэш-функций, которая впервые была предложена Менделем и др. в [5] для атаки Grøstl и Whirlpool с усеченным количеством раундов. Основная идея данной технологии состоит в построении дифференциального пути с использованием доступных степеней свободы для соответствия фрагментам с низкой вероятностью. Обычно она состоит из внутренней фазы, включающей поиск соответствия посередине (match-in-the-middle), и из последующей вероятностной внешней фазы.
С помощью rebound-технологии мы находим коллизии для 4,5 и 5,5-раундовой функции сжатия ГОСТ Р. Более того, используя доступные степени свободы схемы расширения ключа, как в [6], мы усиливаем результаты до коллизий для 7,5 и 9,5 раунда.
В rebound-атаке блочный шифр или перестановка хэш-функции, используемая в функции сжатия, делится на три составные части. Пусть E – блочный шифр, тогда . Rebound-атака делится на две фазы:
. Rebound-атака делится на две фазы:
Перед описанием rebound-атаки на алгоритм ГОСТ Р мы кратко опишем некоторые свойства его линейного преобразования L и табличной замены функции сжатия.

может быть только 0, 2, 4, 6, 8 и 256, что возникает с частотой 38235, 22454, 4377, 444, 25 и 1, соответственно. В среднем, для случайно выбранного дифференциала (a, b) можно ожидать нахождения одного значения в качестве решения. И таблица входных/выходных разностей размером 256 x 256 может помочь найти решения с незначительными вычислениями.
В данном разделе мы опишем применение rebound-атаки на функцию сжатия алгоритма ГОСТ Р, усеченную до 4,5 раунда. Ядром атаки является 4-раундовый дифференциальный путь со следующей последовательностью активных S-боксов:


Рис. 2. Схематическое изображение атаки на 4,5 раунда функции сжатия ГОСТ Р. Активные байты состояния выделены черным
В rebound-атаке мы прежде всего разделяем блочный шифр E на три субшифра . Как показано на рис. 2, наиболее ресурсоемкая часть дифференциального пути сокрыта во внутренней фазе. Доступные степени свободы используются для обеспечения сохранности дифференциального пути в Ein.
. Как показано на рис. 2, наиболее ресурсоемкая часть дифференциального пути сокрыта во внутренней фазе. Доступные степени свободы используются для обеспечения сохранности дифференциального пути в Ein.
На первом шаге внутренней фазы мы начинаем с 8-байтной разности одновременно на стадиях R2P и R3L и продвигаемся вперед и назад к R3 и R3S соответственно (см. рис. 2). Согласно свойствам распространения разности операции L, описанным в разделе 3.2, мы получаем полностью активное состояние как в R3, так и в R3S.
На втором шаге внутренней фазы мы выполняем поиск соответствия на уровне S в r3 с целью поиска подходящего сочетания входной/выходной разности. Как показано в разделе 3.2, мы ожидаем найти в среднем одно решение для заданного дифференциального пути. Стоит отметить, что всего существует 2128 различных дифференциальных путей, и мы можем получить не более 2128 актуальных значений для R3 и R3S. Поскольку k3 может иметь любое значение, максимальное количество стартовых точек равно 2128+512 = 2640.
На внешней фазе мы используем стартовые точки, выработанные на внутренней фазе, и обрабатываем их значения в прямом и обратном направлении. Как показано на рис. 2, разности в R2P и R3L приводят к разностям только в первых столбцах в R1 и R5P соответственно.
Можно легко сконструировать коллизию для функции сжатия ГОСТ Р, усеченной до 4,5 раунда, используя значения, сгенерированные на предыдущем шаге. Поскольку , для идентичных значений h и k одна и та же разность для m и E(k, m) всегда приводит к коллизии. Для пары значений, сгенерированных на внешней фазе, разность эквивалентна для m и E(k, m) с вероятностью 2-64. Следовательно, мы должны сгенерировать около 264 стартовых точек для конструирования коллизии. Трудоемкость этого составляет около 264. Поскольку нам необходимо хранить только таблицу 256 x 256 входных/выходных разностей для таблицы замен, требования к памяти составляют только 216 байт.
, для идентичных значений h и k одна и та же разность для m и E(k, m) всегда приводит к коллизии. Для пары значений, сгенерированных на внешней фазе, разность эквивалентна для m и E(k, m) с вероятностью 2-64. Следовательно, мы должны сгенерировать около 264 стартовых точек для конструирования коллизии. Трудоемкость этого составляет около 264. Поскольку нам необходимо хранить только таблицу 256 x 256 входных/выходных разностей для таблицы замен, требования к памяти составляют только 216 байт.
Используя технологию расширенной замены [7], мы можем усилить 4,5-раундовый результат путем добавления одного раунда к внутренней фазе. Это приводит к атаке на 5,5-раундовую функцию сжатия ГОСТ Р. Внешняя фаза данной атаки – такая же, как и в атаке на 4,5 раунда, а новая последовательность активных S-боксов такова:


Рис. 3. Внутренняя фаза атаки на 5,5-раундовую функцию сжатия ГОСТ Р
Как показано на рис. 3, значения в каждой строке R4S зависят только от соответствующего столбца R3. Другими словами, зная пару значений столбца на стадии R3, поскольку k4 нам известно, мы можем рассчитать значения соответствующей строки R4S. Следовательно, мы можем считать расширенной заменой соответствие между каждым столбцом R3 и соответствующей строкой R4S. Для каждой расширенной замены со случайно заданной входной и выходной разностью мы рассчитываем найти в среднем одно действительное значение.
Далее мы описываем атаку на 5,5 раунда в деталях.
Внутренняя фаза rebound-атаки на 5,5 раунда ГОСТ Р может быть описана следующим образом:
Мы можем выбрать другие разности на стадии R2P для получения большего количества действительных значений, удовлетворяющих разностям. Для входной разности в R2P мы предполагаем найти около 264 стартовых точек.
Внешняя фаза – такая же, как и в 4,5-раундовой атаке, где нам требуется 264 стартовых точек. Следовательно, трудоемкость и требования к памяти для поиска 5,5-раундовой коллизии составляют по 264.
Мы можем улучшить 4,5-раундовые результаты добавлением 3 раундов к внутренней фазе путем использования степеней свободы за счет схемы расширения ключа, как в [6]. Основная идея состоит в разделении внутренней фазы на две субфазы. Эти две субфазы могут быть впоследствии объединены путем полного использования степеней свободы в процедуре расширения ключа. Как результат, мы получаем коллизию для функции сжатия ГОСТ Р, усеченной до 7,5 раунда.
Для усиленной внутренней фазы мы используем следующую последовательность активных байт:

Внутренняя фаза, в свою очередь, разделяется на две субфазы с целью нахождения входных значений, соответствующих дифференциальному пути (рис. 4). На первой субфазе мы выполняем поиск соответствия для раундов 1-2 и 4-5. А на второй субфазе мы объединяем активные значения состояния между r2 и r4, используя степени свободы путем подбора значения раундового ключа.

Рис. 4. Внутренняя фаза поиска коллизии для 7,5-раундовой функции сжатия ГОСТ Р
На данной субфазе мы выполняем поиск соответствия для раундов 1-2 и 4-5, что может быть описано следующим образом:
1. Раунды 1-2:
2. Раунды 4-5: выполняем то же самое, что и для раундов 1-2.
Теперь, после выполнения первой субфазы атаки с трудоемкостью около 29 раундовых преобразований мы имеем 264 кандидатов для R2S, а также для R5.
В рамках второй субфазы мы должны объединить разности в R2S и разности в R5, а также действительные значения, используя степени свободы в схеме расширения ключа. Это означает, что мы должны решить следующее уравнение:

при

Для 264 кандидатов в R2S и 264 кандидатов в R5 с учетом 512 степеней свободы значений k3, k4 и k5 мы рассчитываем найти 264 решений. Поскольку LP(R2S) = R2L и (X[k5])-1 = X[k5], мы можем переписать (8) следующим образом:

Поскольку мы всегда можем поменять порядок P и S и

мы получаем следующее уравнение:

Вводим обозначения и T = P-1L-1(R5), тогда приведенное выше уравнение может быть переписано так:
и T = P-1L-1(R5), тогда приведенное выше уравнение может быть переписано так:

Решение данного уравнения эквивалентно соединению разностей и значений R2S и R5. Мы опишем метод, используемый для решения уравнения, далее.

Рис. 5. Внутренняя субфаза 2 атаки по нахождению коллизии для 7,5-раундовой функции сжатия ГОСТ Р
Поскольку разность в R2L и R4S фиксируется в рамках субфазы 1, разности в R2* и T также фиксированы. И 264 значений для состояний R2S и R5, сгенерированных на субфазе 1, непосредственно приводят к 264 значениям для R2* и T соответственно. Теперь мы можем решить (15) для каждой строки независимо, как показано на рис. 5, что может быть описано следующим образом:
1. Вычисляем 8-байтные разности и 264 значений для R2* из R2S и вычисляем 8-байтные разности и соответствующие 264 значений для T из R5. Нам только необходимо вычислить и сохранить строку значений для R2* и T, поскольку мы можем решать уравнение построчно. Трудоемкость и требования к памяти этого шага составляют по 29 вместо 265.
2. Для всех 264 значений первой строки R3* повторяем следующие шаги:
3. На этом шаге мы соединяем значения строк 2-8 для соответствующих R2* и T, полученных на предыдущем шаге. Для каждой строки независимо выполняется исчерпывающий поиск по всем 264 значениям соответствующей строки ключа k3*. Отметим, что мы хотим соединить 64-битные значения, и проверкой 264 ключевых значений мы рассчитываем всегда найти решение.
После всех этих шагов мы получаем 264 соответствующих значений, соединяющих R2* и T. Другими словами, мы получаем 264 стартовые точки для внешней фазы. Трудоемкость составляет около 2128 раундовых преобразований при требованиях к памяти около 216 байт. В среднем, мы рассчитываем найти стартовую точку с трудоемкостью 264. Шаг 3 может быть пропущен применением таблицы подстановки размером 2128. С помощью таблицы подстановки мы рассчитываем найти стартовую точку со средней трудоемкостью 1. Однако, трудоемкость построения таблицы подстановки составляет 2128, а требования к памяти – 2128 байт. Отметим, что существуют 264 разностей для R3 и 264 разностей для R4S. Для фиксированной пары разностей в R3 и R4S мы ожидаем найти 264 стартовых точки. Таким образом, суммарно нам необходимо сгенерировать не более 2192 стартовых точек для внешней фазы.
Внешняя фаза 7,5-раундовой атаки аналогична 4,5-раундовой атаке. Атака по поиску коллизий на 7,5 раунда использует следующую последовательность активных байт:

Трудоемкость поиска коллизии для 7,5 раунда функции сжатия ГОСТ Р составляет около 264+64 = 2128 при требованиях к памяти 216 байт.
Хотя мы можем получить более 2192 стартовых точек, для внешней фазы 7,5-раундовой атаки требуется только 264 из них. Мы можем расширить внешнюю фазу добавлением одного раунда в начале и одного раунда в конце для конструирования атаки по нахождению коллизий для 9,5 раунда. Такая атака использует следующую последовательность активных байт:

Далее мы опишем внешнюю фазу 9,5-раундовой атаки в деталях.

Рис. 6. Схематичное изображение атаки для 9,5-раундовой функции сжатия ГОСТ Р
В отличие от внешней фазы атаки на 7,5 раунда, здесь мы используем усеченные дифференциалы. После выполнения внутренней фазы сгенерированные значения приводят к 8-байтной разности в R3 и R8, как показано на рис. 6. Мы хотим найти соответствие усеченному дифференциальному пути 8 → 1 в обоих направлениях. Вероятность данного усеченного дифференциального пути составляет 2-56. 1-байтовая разность в R2 и R9 всегда приводит к 8 активным байтам для R1 и R10. Следовательно, вероятность внешней фазы составляет 2-112. Поэтому мы должны сгенерировать в 2112 раз больше стартовых точек.
Поскольку коллизия функции сжатия, усеченной до 9,5 раунда, требует той же самой разности в m и в R10P, мы должны сгенерировать всего 2112+64 = 2176 стартовых точек. Как описано в разделе 3.5, мы рассчитываем найти одну стартовую точку с трудоемкостью 264. Поэтому трудоемкость нахождения коллизии для 9,5 раунда составляет примерно 264+176 = 2240, а требования к памяти – 216 байт. При использовании таблицы подстановок с 2128 значениями трудоемкость составляет 2176 при требованиях к памяти 2128 байт.
В данной главе мы представляем различитель для функции сжатия ГОСТ Р, усеченной до 10 раундов.
Предложенный Жильбером и др. в [7] вид различителей может быть описан следующим образом: для случайной функции, которая выполняет b-битную перестановку, отображение входной разности из подпространства размером I в выходную разность из подпространства размером J требует только max{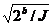 , 2b/(IJ)} вызовов функции (без потери общности мы предполагаем, что I ≤ J).
, 2b/(IJ)} вызовов функции (без потери общности мы предполагаем, что I ≤ J).
Путем применения L и X[k11] к предыдущему результату для 9,5 раунда, мы расширяем дифференциальный путь до 10 раундов. Даже хотя R11 является полностью активным в терминах усеченных дифференциалов, разности в R11 по-прежнему принадлежат подпространству размерностью не более 64. Поскольку входные разности функции сжатия принадлежат подпространству размером 264, выходные разности принадлежат подпространству размером 2128. Для случайной функции нам требуется 2512-(64+128) = 2320 вычислений для полного определения соответствия входных и выходных разностей такого вида. Но для функции сжатия, усеченной до 10 раундов, трудоемкость составляет только 2176 при требованиях к памяти 216 или 2128 при требованиях к памяти 2128. Трудоемкость, требуемая для функции сжатия, намного меньше таковой для случайной функции. Это свойство может быть использовано для того, чтобы отличить функцию сжатия ГОСТ Р от случайной функции.
Теперь мы рассмотрим стойкость структуры хэш-функции ГОСТ Р. Для структуры такого типа мы предлагаем метод конструирования k-коллизий. Трудоемкость при этом существенно меньше трудоемкости конструирования k-коллизии для идеальной структуры. Другими словами, мы доказываем, что данный вид структуры не является идеальным.
Для идеальной хэш-функции с n-битным выходным значением трудоемкость поиска пары, дающей коллизию, составляет примерно 2n/2, а для поиска k-коллизии (мультиколлизии) – 2n(k-1)/k. Однако, основываясь на попарных коллизиях, Жуа на Crypto’04 [12] предложил метод конструирования 2t-коллизий для итеративной структуры с трудоемкостью всего t x 2n/2. Как показано на рис. 7, атакующий сначала генерирует t различных попарных коллизий {(B1, B1*), (B2, B2*), …, (Bt, Bt*)}. Затем атакующий может сразу получить 2t-коллизию вида (b1, b2,…, bt), где bi – один из двух блоков Bi и Bi*.

Рис. 7. Схема 2t-коллизии Жуа. 2t сообщений имеют вид (b1, b2,…, bt), где bi – один из двух блоков Bi и Bi*
Несмотря на то, что структура ГОСТ Р не является итеративной, для нее мы также можем сконструировать k-коллизию. Данный метод состоит в следующем:
1. Как показано на рис. 8, генерируем 2t сообщений, приводящих к одному и тому же значению ht:
2. Среди 2t сообщений, сгенерированных на шаге 1, пытаемся найти k коллизий в ∑ и получаем k сообщений в результате. Отметим, что все 2t сообщений имеют одно и то же значение N, а эти k сообщений всегда приводят к k-коллизии хэш-функции ГОСТ Р.

Рис. 8. Схематическое изображение конструирования k коллизий для ГОСТ Р
Поскольку все блоки сообщений шага 1 имеют форму 0256 || {0, 1}256 и ∑ = b1 b2
b2  …
… bt, значащих бит в ∑ не более log2t + 256. В идеальной модели шаг 2 требует
bt, значащих бит в ∑ не более log2t + 256. В идеальной модели шаг 2 требует  сообщений для конструирования k коллизий ∑, что требует соответствия следующим неравенствам, в которых
сообщений для конструирования k коллизий ∑, что требует соответствия следующим неравенствам, в которых

Решая приведенные выше неравенства, мы имеем:
176 ≤ t ≤ 2256
и

Другими словами, для t-блочного сообщения, где 176 ≤ t ≤ 2256, мы можем найти k-коллизию хэш-функции ГОСТ Р, выполнив только вычислений. Данная трудоемкость существенно меньше, чем трудоемкость нахождения k-коллизии для хэш-функции идеальной структуры.
вычислений. Данная трудоемкость существенно меньше, чем трудоемкость нахождения k-коллизии для хэш-функции идеальной структуры.
В данной работе мы представили некоторые криптоаналитические результаты для ГОСТ Р. Сначала мы описали нашу атаку на 4,5-раундовую функцию сжатия ГОСТ Р с применением технологии rebound-атаки. Далее данный результат был усилен до 5,5 раунда с использованием технологии расширенной замены. Затем степени свободы схемы расширения ключа были использованы для достижения атак на 7,5 раунда и 9,5 раунда. Более того, используя результат 9,5-раундовой атаки, мы представили 10-раундовый различитель для функции сжатия ГОСТ Р. В завершение работы мы презентовали метод конструирования k-коллизий для хэш-функции ГОСТ Р, который показывает слабость структуры, использованной в ГОСТ Р.
На текущий момент известно несколько работ, посвященных криптоанализу ГОСТ Р 34.11-2012. Но именно в работе Zongyue Wang, Hongbo Yu и Xiaoyun Wang «Cryptanalysis of GOST R Hash Function» предложены наиболее эффективные атаки на данный алгоритм. Поэтому, на мой взгляд, именно эта работа представляет наибольший интерес среди работ по данной теме; ее перевод я и предлагаю вашему вниманию.
В переводе сохранены авторские названия стандартов хэширования: под названием «ГОСТ» имеется в виду стандарт 1994 года ГОСТ Р 34.11-94, а «ГОСТ Р» обозначает исследуемый в работе алгоритм ГОСТ Р 34.11-2012.
Работа переведена и публикуется на русском языке с разрешения ее авторов.
Аннотация
ГОСТ Р – это стандарт на хэш-функцию в России. Данная работа представляет некоторые результаты криптоанализа ГОСТ Р. Используя приемы rebound-атак, мы получили атаки, позволяющие найти коллизии функции сжатия с уменьшенным количеством раундов. Предложена атака на 9,5 раунда с трудоемкостью 2176 операций и требованиями к памяти 2128 байт. На основе данной атаки предложен различитель (Прим. перев.: различитель – алгоритм, позволяющий отличить атакуемую функцию от случайно и равновероятно выбранной функции). Более того, представлен метод конструирования k-коллизий для 512-битной версии ГОСТ Р, который показывает слабость структуры, использованной в ГОСТ Р. Насколько нам известно, это первые результаты по анализу ГОСТ Р.
Ключевые слова: хэш-функция, ГОСТ Р, rebound-атака, мультиколлизия.
1. Введение
Хэш-функции играют важную роль в криптографии и используются во многих приложениях, например, электронной подписи, аутентификации и обеспечения целостности данных. С момента взлома алгоритмов MD5 и SHA-1 [1, 2] криптографы находятся в поиске стойких и эффективных хэш-функций. Преемник алгоритма ГОСТ, ГОСТ Р является стандартом хэширования в России [3]. Похожий по своей структуре на Whirlpool [4], он также использует подобный AES блочный шифр в своей функции сжатия.
Rebound-атака – это технология использования степеней свободы, которая может быть применена для поиска коллизий для алгоритмов хэширования, основанных как на перестановках, так и на блочных шифрах. Данная технология была впервые предложена в работе Менделя (Mendel) и др. для формирования атак по поиску коллизий для усеченных алгоритмов Whirlpool и Grøstl [5]. Она нацелена на эффективный поиск пар значений, которые соответствуют предопределенному усеченному дифференциалу. Процедура поиска разделяется на две фазы: внутренняя (inbound) фаза и внешняя (outbound) фаза. Во внутренней фазе атакующий полностью использует доступные степени свободы и генерирует достаточно много пар значений, удовлетворяющих пути усеченного дифференциала внутренней фазы, используемых в качестве точек старта. Впоследствии, во внешней фазе данные точки старта проверяются с целью поиска пар значений, удовлетворяющих пути усеченного дифференциала внешней фазы.
Ламберже (Lamberger) и др. усилили данную технологию в [6] и получили улучшенные результаты для Whirlpool. Доступные степени свободы в ключевой схеме используются для расширения внутренней фазы rebound-атаки на величину до двух раундов. Лучшие результаты работы [6] – это почти-коллизия (near-collision) для 9,5 раунда функции сжатия с трудоемкостью 2176. Данный результат затем использовался для построения первого алгоритма различения для полной 10-раундовой функции сжатия алгоритма Whirlpool. В то же самое время Жильбер (Gilbert) и др. предложили технологию расширенной замены (Super-Sbox) для rebound-атаки в [7], где два раунда AES-подобных преобразований рассматривались как один уровень расширенной замены. Кроме того, rebound-атака может также быть применена для анализа AES и AES-подобных блочных шифров [8, 9], а равно и ARX-шифров (Прим. перев.: ARX – аббревиатура от Add-Rotate-Xor, данные операции являются основными в ARX-шифрах). [10]. Недавно, с использованием адаптированной технологии rebound-атаки, Дюк (Duc) и др. сконструировали дифференциальные характеристики для Keccak в [11].
В качестве альтернативы поиску коллизий для хэш-функций, Жуа (Joux) предложил метод конструирования мультиколлизий в [12]. Он показал, что для итеративной хэш-функции поиск мультиколлизии вовсе не сложнее поиска одиночной коллизии. Этот метод может быть применим в большинстве случаев для анализа стойкости структуры хэш-функции.
1.1. Наш вклад
Ввиду схожести структуры ГОСТ Р и Whirlpool, rebound-атака, использованная в [6] для анализа Whirlpool, может быть также применима к ГОСТ Р. Однако, ГОСТ Р использует матричную перестановку вместо операции ShiftRows в AES-подобных структурах. Мы покажем, что эта разница приводит к большей уязвимости.
В данной работе мы представляем первые результаты анализа ГОСТ Р. Более точно, применив методы rebound-атаки, схожие с приведенными в [6], мы получили атаки по поиску коллизии для 4,5, 5,5, 7,5 и 9,5 раунда функции сжатия ГОСТ Р. Наши атаки по поиску коллизий для функции сжатия ГОСТ Р приведены в табл. 1. Далее мы показали, что атака на 9,5 раунда может быть впоследствии сконвертирована в 10-раундовый различитель. Кроме того, мы предложили метод конструирования мультиколлизий для полной 512-битной версии ГОСТ Р. Этот результат показывает, что структура, использованная в ГОСТ Р, не является идеальной.
Табл. 1. Сводные результаты для функции сжатия ГОСТ Р. Ресурсоемкость, указанная в скобках, относится к модифицированным атакам, использующим предвычисляемую таблицу, для заполнения которой требуется 2128 единиц времени и памяти.
| Раунды | Трудоемкость / память | Тип | Описание |
| 4,5 | 264 / 216 | Коллизия | Раздел 3.3 |
| 5,5 | 264 / 264 | Коллизия | Раздел 3.4 |
| 7,5 | 2128 / 216 | Коллизия | Раздел 3.5 |
| 9,5 | 2240 / 216 (2176 / 2128) | Коллизия | Раздел 3.6 |
1.2. Содержание работы
Краткое содержание данной работы: в главе 2 мы кратко опишем хэш-функцию ГОСТ Р. Затем мы приведем подробное описание rebound-атаки в главе 3; описание различителя будет дано в главе 4. В главе 5 мы представим метод конструирования мультиколлизий. Наконец, в главе 6 мы подведем итоги работы.
2. Хэш-функция ГОСТ Р
ГОСТ Р – это стандарт хэширования в России [3]. Он обрабатывает блоки сообщений размером 512 бит и вычисляет 512- или 256-битные хэш-значения. l-битное сообщение сначала дополняется до размера, кратного 512 битам. Единичный бит присоединяется к концу сообщения; после него следуют 512 - 1 - (l mod 512) нулевых бит. Пусть M = Mt || Mt-1 ||…|| M1 – это сообщение, состоящее из t блоков после дополнения, представленное в big-endian форме. Тогда, как показано на рис. 1, вычисление H(M) можно описать следующим образом:

Рис. 1. Хэш-функция ГОСТ Р

где IV – предопределенное начальное значение, а
Используемый в ГОСТ Р блочный шифр E представляет собой вариант AES, который обновляет 64-байтное состояние (представленное как массив 8 x 8 – состояние можно представить также как 64 x 64 в поле GF(2)) и раундовый ключ, выполняя 12 раундов. В каждом раунде состояние обновляется выполнением раундового преобразования ri следующим образом:
Раундовое преобразование состоит из:
- уровня нелинейных преобразований S, на котором к каждому байту состояния независимо применяется табличная замена;
- байтовой перестановки P, переставляющей элементы матрицы состояния;
- линейного преобразования L, представляющего собой независимое умножение справа каждой строки состояния на 64 x 64 матрицу A в поле GF(2);
- операции X[ki+1], выполняющей наложение раундового ключа ki+1 на состояние операцией XOR.
Раундовый ключ ki вычисляется так:
где Ci – константы алгоритма ГОСТ Р, а начальное значение k1 определяется как
После последнего раунда преобразования, обновляющего состояние, выходное значение блочного шифра E, предыдущее значение состояния hj-1 и блок сообщения Mj объединяются операцией XOR в качестве выходного значения функции сжатия.
Мы обозначим результат раундового преобразования ri как Ri+1, а промежуточные состояния после преобразований S, P и L как, соответственно, RiS, RiP и RiL. Начальное состояние
3. Rebound-атака на функцию сжатия ГОСТ Р
Rebound-атака – это технология анализа хэш-функций, которая впервые была предложена Менделем и др. в [5] для атаки Grøstl и Whirlpool с усеченным количеством раундов. Основная идея данной технологии состоит в построении дифференциального пути с использованием доступных степеней свободы для соответствия фрагментам с низкой вероятностью. Обычно она состоит из внутренней фазы, включающей поиск соответствия посередине (match-in-the-middle), и из последующей вероятностной внешней фазы.
С помощью rebound-технологии мы находим коллизии для 4,5 и 5,5-раундовой функции сжатия ГОСТ Р. Более того, используя доступные степени свободы схемы расширения ключа, как в [6], мы усиливаем результаты до коллизий для 7,5 и 9,5 раунда.
3.1. Оригинальная rebound-атака
В rebound-атаке блочный шифр или перестановка хэш-функции, используемая в функции сжатия, делится на три составные части. Пусть E – блочный шифр, тогда
- Внутренняя фаза: эта фаза стартует с нескольких выбранных входных/выходных разностей в Ein, которые распространяются через линейный уровень в прямом и обратном направлении. Затем генерируются все возможные пары актуальных значений, которые удовлетворяют требуемой разности и соответствуют разностям после одного уровня табличной замены. Эти фактические пары значений являются стартовыми точками для внешней фазы.
- Внешняя фаза: подобранные пары внутренней фазы используются в вычислениях в прямом и обратном направлении через Efw и Ebw для получения желательных коллизий или почти-коллизий. Обычно Efw и Ebw имеют низкую вероятность, так что необходимо повторять внутреннюю фазу для получения большего количества стартовых точек.
3.2. Предварительные выкладки для rebound-атаки
Перед описанием rebound-атаки на алгоритм ГОСТ Р мы кратко опишем некоторые свойства его линейного преобразования L и табличной замены функции сжатия.
- Распространение разности в L: поскольку L – это линейное преобразование, определенная входная разность в L приводит к определенной выходной разности. Поскольку L действует на каждую строку состояния независимо, выходная разность определенной строки зависит только от входной разности этой строки. При наличии единственного активного байта строки преобразование L всегда приводит к восьми активным байтам, как в прямом, так и в обратном направлении, независимо от позиции активного байта.
- Дифференциальные свойства S: для определенных
 , количество решений равенства
, количество решений равенства
может быть только 0, 2, 4, 6, 8 и 256, что возникает с частотой 38235, 22454, 4377, 444, 25 и 1, соответственно. В среднем, для случайно выбранного дифференциала (a, b) можно ожидать нахождения одного значения в качестве решения. И таблица входных/выходных разностей размером 256 x 256 может помочь найти решения с незначительными вычислениями.
3.3. Нахождение коллизий для 4,5-раундовой функции сжатия ГОСТ Р
В данном разделе мы опишем применение rebound-атаки на функцию сжатия алгоритма ГОСТ Р, усеченную до 4,5 раунда. Ядром атаки является 4-раундовый дифференциальный путь со следующей последовательностью активных S-боксов:

Рис. 2. Схематическое изображение атаки на 4,5 раунда функции сжатия ГОСТ Р. Активные байты состояния выделены черным
В rebound-атаке мы прежде всего разделяем блочный шифр E на три субшифра
3.3.1. Внутренняя фаза
На первом шаге внутренней фазы мы начинаем с 8-байтной разности одновременно на стадиях R2P и R3L и продвигаемся вперед и назад к R3 и R3S соответственно (см. рис. 2). Согласно свойствам распространения разности операции L, описанным в разделе 3.2, мы получаем полностью активное состояние как в R3, так и в R3S.
На втором шаге внутренней фазы мы выполняем поиск соответствия на уровне S в r3 с целью поиска подходящего сочетания входной/выходной разности. Как показано в разделе 3.2, мы ожидаем найти в среднем одно решение для заданного дифференциального пути. Стоит отметить, что всего существует 2128 различных дифференциальных путей, и мы можем получить не более 2128 актуальных значений для R3 и R3S. Поскольку k3 может иметь любое значение, максимальное количество стартовых точек равно 2128+512 = 2640.
3.3.2. Внешняя фаза
На внешней фазе мы используем стартовые точки, выработанные на внутренней фазе, и обрабатываем их значения в прямом и обратном направлении. Как показано на рис. 2, разности в R2P и R3L приводят к разностям только в первых столбцах в R1 и R5P соответственно.
Можно легко сконструировать коллизию для функции сжатия ГОСТ Р, усеченной до 4,5 раунда, используя значения, сгенерированные на предыдущем шаге. Поскольку
3.4. Нахождение коллизий для 5,5-раундовой функции сжатия ГОСТ Р
Используя технологию расширенной замены [7], мы можем усилить 4,5-раундовый результат путем добавления одного раунда к внутренней фазе. Это приводит к атаке на 5,5-раундовую функцию сжатия ГОСТ Р. Внешняя фаза данной атаки – такая же, как и в атаке на 4,5 раунда, а новая последовательность активных S-боксов такова:

Рис. 3. Внутренняя фаза атаки на 5,5-раундовую функцию сжатия ГОСТ Р
Как показано на рис. 3, значения в каждой строке R4S зависят только от соответствующего столбца R3. Другими словами, зная пару значений столбца на стадии R3, поскольку k4 нам известно, мы можем рассчитать значения соответствующей строки R4S. Следовательно, мы можем считать расширенной заменой соответствие между каждым столбцом R3 и соответствующей строкой R4S. Для каждой расширенной замены со случайно заданной входной и выходной разностью мы рассчитываем найти в среднем одно действительное значение.
Далее мы описываем атаку на 5,5 раунда в деталях.
3.4.1. Внутренняя фаза
Внутренняя фаза rebound-атаки на 5,5 раунда ГОСТ Р может быть описана следующим образом:
- Начинаем с разности в 8 активных байтах в первом столбце R2P и продвигаемся вперед до R3.
- Для каждой независимой расширенной замены, зная ее входную разность, обрабатываем все 264 пар входных значений и вычисляем замену вперед. Это дает нам 264 значений выходных разностей. Для каждой полученной разности сохраняем соответствующие пары входных значений, приводящих к ней. Эта фаза требует около 264 операций и памяти.
- Для каждой 8-байтной разности в R4L продвигаемся назад до R4S. Проверяем все сохраненные ранее значения на присутствие требуемой разности.
Мы можем выбрать другие разности на стадии R2P для получения большего количества действительных значений, удовлетворяющих разностям. Для входной разности в R2P мы предполагаем найти около 264 стартовых точек.
3.4.2. Внешняя фаза
Внешняя фаза – такая же, как и в 4,5-раундовой атаке, где нам требуется 264 стартовых точек. Следовательно, трудоемкость и требования к памяти для поиска 5,5-раундовой коллизии составляют по 264.
3.5. Нахождение коллизий для 7,5-раундовой функции сжатия ГОСТ Р
Мы можем улучшить 4,5-раундовые результаты добавлением 3 раундов к внутренней фазе путем использования степеней свободы за счет схемы расширения ключа, как в [6]. Основная идея состоит в разделении внутренней фазы на две субфазы. Эти две субфазы могут быть впоследствии объединены путем полного использования степеней свободы в процедуре расширения ключа. Как результат, мы получаем коллизию для функции сжатия ГОСТ Р, усеченной до 7,5 раунда.
Для усиленной внутренней фазы мы используем следующую последовательность активных байт:
Внутренняя фаза, в свою очередь, разделяется на две субфазы с целью нахождения входных значений, соответствующих дифференциальному пути (рис. 4). На первой субфазе мы выполняем поиск соответствия для раундов 1-2 и 4-5. А на второй субфазе мы объединяем активные значения состояния между r2 и r4, используя степени свободы путем подбора значения раундового ключа.

Рис. 4. Внутренняя фаза поиска коллизии для 7,5-раундовой функции сжатия ГОСТ Р
3.5.1. Внутренняя субфаза 1
На данной субфазе мы выполняем поиск соответствия для раундов 1-2 и 4-5, что может быть описано следующим образом:
1. Раунды 1-2:
- Начинаем с разности в 8 байтах в первом столбце R3 и продвигаемся в обратном направлении к R2S.
- Для каждой разности в 8 байтах в первом столбце R1P продвигаемся вперед до R2. Поскольку различных значений разности в R1P всего 264, мы можем получить 264 разностей для R2. После поиска соответствия данные разности приводят примерно к 264 действительным значениям. Однако, мы можем выполнять поиск соответствия для каждой строки независимо и получать 28 действительных значений для строки. Следовательно, трудоемкость генерации 264 действительных значений, соответствующих дифференциальному пути, составляет всего 28 раундовых преобразований.
2. Раунды 4-5: выполняем то же самое, что и для раундов 1-2.
Теперь, после выполнения первой субфазы атаки с трудоемкостью около 29 раундовых преобразований мы имеем 264 кандидатов для R2S, а также для R5.
3.5.2. Внутренняя субфаза 2
В рамках второй субфазы мы должны объединить разности в R2S и разности в R5, а также действительные значения, используя степени свободы в схеме расширения ключа. Это означает, что мы должны решить следующее уравнение:
при
Для 264 кандидатов в R2S и 264 кандидатов в R5 с учетом 512 степеней свободы значений k3, k4 и k5 мы рассчитываем найти 264 решений. Поскольку LP(R2S) = R2L и (X[k5])-1 = X[k5], мы можем переписать (8) следующим образом:
Поскольку мы всегда можем поменять порядок P и S и
мы получаем следующее уравнение:
Вводим обозначения
Решение данного уравнения эквивалентно соединению разностей и значений R2S и R5. Мы опишем метод, используемый для решения уравнения, далее.

Рис. 5. Внутренняя субфаза 2 атаки по нахождению коллизии для 7,5-раундовой функции сжатия ГОСТ Р
Поскольку разность в R2L и R4S фиксируется в рамках субфазы 1, разности в R2* и T также фиксированы. И 264 значений для состояний R2S и R5, сгенерированных на субфазе 1, непосредственно приводят к 264 значениям для R2* и T соответственно. Теперь мы можем решить (15) для каждой строки независимо, как показано на рис. 5, что может быть описано следующим образом:
1. Вычисляем 8-байтные разности и 264 значений для R2* из R2S и вычисляем 8-байтные разности и соответствующие 264 значений для T из R5. Нам только необходимо вычислить и сохранить строку значений для R2* и T, поскольку мы можем решать уравнение построчно. Трудоемкость и требования к памяти этого шага составляют по 29 вместо 265.
2. Для всех 264 значений первой строки R3* повторяем следующие шаги:
- Поскольку разность в R3* известна, для выбранного значения первой строки R3* вычисляем в прямом направлении значения первой строки R3L и разность для первой строки R4.
- После выполнения поиска соответствия для разности первой строки R4 и R4S мы рассчитываем найти решение для первой строки R4. Поскольку первая строка значений R3L нам известна, мы можем далее вычислить значение первой строки k4.
- Вычисляем первые строки для k3*, R2*, R4S и T. Поскольку для первой строки как R2*, так и R4S мы имеем около 264 значений, мы рассчитываем найти соответствие между ними. Другими словами, мы теперь соединили и значения, и разности для первой строки.
3. На этом шаге мы соединяем значения строк 2-8 для соответствующих R2* и T, полученных на предыдущем шаге. Для каждой строки независимо выполняется исчерпывающий поиск по всем 264 значениям соответствующей строки ключа k3*. Отметим, что мы хотим соединить 64-битные значения, и проверкой 264 ключевых значений мы рассчитываем всегда найти решение.
После всех этих шагов мы получаем 264 соответствующих значений, соединяющих R2* и T. Другими словами, мы получаем 264 стартовые точки для внешней фазы. Трудоемкость составляет около 2128 раундовых преобразований при требованиях к памяти около 216 байт. В среднем, мы рассчитываем найти стартовую точку с трудоемкостью 264. Шаг 3 может быть пропущен применением таблицы подстановки размером 2128. С помощью таблицы подстановки мы рассчитываем найти стартовую точку со средней трудоемкостью 1. Однако, трудоемкость построения таблицы подстановки составляет 2128, а требования к памяти – 2128 байт. Отметим, что существуют 264 разностей для R3 и 264 разностей для R4S. Для фиксированной пары разностей в R3 и R4S мы ожидаем найти 264 стартовых точки. Таким образом, суммарно нам необходимо сгенерировать не более 2192 стартовых точек для внешней фазы.
3.5.3. Внешняя фаза
Внешняя фаза 7,5-раундовой атаки аналогична 4,5-раундовой атаке. Атака по поиску коллизий на 7,5 раунда использует следующую последовательность активных байт:
Трудоемкость поиска коллизии для 7,5 раунда функции сжатия ГОСТ Р составляет около 264+64 = 2128 при требованиях к памяти 216 байт.
3.6. Нахождение коллизий для 9,5-раундовой функции сжатия ГОСТ Р
Хотя мы можем получить более 2192 стартовых точек, для внешней фазы 7,5-раундовой атаки требуется только 264 из них. Мы можем расширить внешнюю фазу добавлением одного раунда в начале и одного раунда в конце для конструирования атаки по нахождению коллизий для 9,5 раунда. Такая атака использует следующую последовательность активных байт:
Далее мы опишем внешнюю фазу 9,5-раундовой атаки в деталях.

Рис. 6. Схематичное изображение атаки для 9,5-раундовой функции сжатия ГОСТ Р
3.6.1. Внешняя фаза
В отличие от внешней фазы атаки на 7,5 раунда, здесь мы используем усеченные дифференциалы. После выполнения внутренней фазы сгенерированные значения приводят к 8-байтной разности в R3 и R8, как показано на рис. 6. Мы хотим найти соответствие усеченному дифференциальному пути 8 → 1 в обоих направлениях. Вероятность данного усеченного дифференциального пути составляет 2-56. 1-байтовая разность в R2 и R9 всегда приводит к 8 активным байтам для R1 и R10. Следовательно, вероятность внешней фазы составляет 2-112. Поэтому мы должны сгенерировать в 2112 раз больше стартовых точек.
Поскольку коллизия функции сжатия, усеченной до 9,5 раунда, требует той же самой разности в m и в R10P, мы должны сгенерировать всего 2112+64 = 2176 стартовых точек. Как описано в разделе 3.5, мы рассчитываем найти одну стартовую точку с трудоемкостью 264. Поэтому трудоемкость нахождения коллизии для 9,5 раунда составляет примерно 264+176 = 2240, а требования к памяти – 216 байт. При использовании таблицы подстановок с 2128 значениями трудоемкость составляет 2176 при требованиях к памяти 2128 байт.
4. Различитель для 10 раундов
В данной главе мы представляем различитель для функции сжатия ГОСТ Р, усеченной до 10 раундов.
Предложенный Жильбером и др. в [7] вид различителей может быть описан следующим образом: для случайной функции, которая выполняет b-битную перестановку, отображение входной разности из подпространства размером I в выходную разность из подпространства размером J требует только max{
Путем применения L и X[k11] к предыдущему результату для 9,5 раунда, мы расширяем дифференциальный путь до 10 раундов. Даже хотя R11 является полностью активным в терминах усеченных дифференциалов, разности в R11 по-прежнему принадлежат подпространству размерностью не более 64. Поскольку входные разности функции сжатия принадлежат подпространству размером 264, выходные разности принадлежат подпространству размером 2128. Для случайной функции нам требуется 2512-(64+128) = 2320 вычислений для полного определения соответствия входных и выходных разностей такого вида. Но для функции сжатия, усеченной до 10 раундов, трудоемкость составляет только 2176 при требованиях к памяти 216 или 2128 при требованиях к памяти 2128. Трудоемкость, требуемая для функции сжатия, намного меньше таковой для случайной функции. Это свойство может быть использовано для того, чтобы отличить функцию сжатия ГОСТ Р от случайной функции.
5. Мультиколлизии хэш-функции ГОСТ Р
Теперь мы рассмотрим стойкость структуры хэш-функции ГОСТ Р. Для структуры такого типа мы предлагаем метод конструирования k-коллизий. Трудоемкость при этом существенно меньше трудоемкости конструирования k-коллизии для идеальной структуры. Другими словами, мы доказываем, что данный вид структуры не является идеальным.
Для идеальной хэш-функции с n-битным выходным значением трудоемкость поиска пары, дающей коллизию, составляет примерно 2n/2, а для поиска k-коллизии (мультиколлизии) – 2n(k-1)/k. Однако, основываясь на попарных коллизиях, Жуа на Crypto’04 [12] предложил метод конструирования 2t-коллизий для итеративной структуры с трудоемкостью всего t x 2n/2. Как показано на рис. 7, атакующий сначала генерирует t различных попарных коллизий {(B1, B1*), (B2, B2*), …, (Bt, Bt*)}. Затем атакующий может сразу получить 2t-коллизию вида (b1, b2,…, bt), где bi – один из двух блоков Bi и Bi*.

Рис. 7. Схема 2t-коллизии Жуа. 2t сообщений имеют вид (b1, b2,…, bt), где bi – один из двух блоков Bi и Bi*
Несмотря на то, что структура ГОСТ Р не является итеративной, для нее мы также можем сконструировать k-коллизию. Данный метод состоит в следующем:
1. Как показано на рис. 8, генерируем 2t сообщений, приводящих к одному и тому же значению ht:
- Пусть h0 будет начальным значением IV алгоритма ГОСТ Р.
- Для i от 1 до t выполняем:
- Поиск таких Bi и Bi*, для которых gN(hi-1, Bi) = gN(hi-1, Bi*), где Bi и Bi* имеют форму 0256 || {0, 1}256. Поскольку всего существует 2256 сообщений такого вида, мы предполагаем найти коллизию с помощью обобщенного парадокса дней рождений [13].
- Составление результирующих 2t сообщений в форме (b1,…, bt), где bi – это один из двух блоков: Bi или Bi*.
2. Среди 2t сообщений, сгенерированных на шаге 1, пытаемся найти k коллизий в ∑ и получаем k сообщений в результате. Отметим, что все 2t сообщений имеют одно и то же значение N, а эти k сообщений всегда приводят к k-коллизии хэш-функции ГОСТ Р.

Рис. 8. Схематическое изображение конструирования k коллизий для ГОСТ Р
Поскольку все блоки сообщений шага 1 имеют форму 0256 || {0, 1}256 и ∑ = b1

Решая приведенные выше неравенства, мы имеем:
176 ≤ t ≤ 2256
и

Другими словами, для t-блочного сообщения, где 176 ≤ t ≤ 2256, мы можем найти k-коллизию хэш-функции ГОСТ Р, выполнив только
6. Заключение
В данной работе мы представили некоторые криптоаналитические результаты для ГОСТ Р. Сначала мы описали нашу атаку на 4,5-раундовую функцию сжатия ГОСТ Р с применением технологии rebound-атаки. Далее данный результат был усилен до 5,5 раунда с использованием технологии расширенной замены. Затем степени свободы схемы расширения ключа были использованы для достижения атак на 7,5 раунда и 9,5 раунда. Более того, используя результат 9,5-раундовой атаки, мы представили 10-раундовый различитель для функции сжатия ГОСТ Р. В завершение работы мы презентовали метод конструирования k-коллизий для хэш-функции ГОСТ Р, который показывает слабость структуры, использованной в ГОСТ Р.
Литература
- X. Wang, H. Yu, How to Break MD5 and Other Hash Functions, in: Advances in Cryptology–EUROCRYPT 2005, Springer, 2005, pp. 19–35.
- X. Wang, Y. L. Yin, H. Yu, Finding Collisions in the Full SHA-1, in: Advances in Cryptology–CRYPTO 2005, Springer, 2005, pp. 17–36.
- V. Dolmatov, Gost R 34.11-94: Hash function algorithm.
- P. Barreto, V. Rijmen, The Whirlpool Hashing Function, in: First open NESSIE Workshop, Leuven, Belgium, Vol. 13, 2000, p. 14.
- F. Mendel, C. Rechberger, M. Schläffer, S. S. Thomsen, The Rebound Attack: Cryptanalysis of Reduced Whirlpool and Grøstl, in: Fast Software Encryption, Springer, 2009, pp. 260–276.
- M. Lamberger, F. Mendel, C. Rechberger, V. Rijmen, M. Schläffer, Rebound Distinguishers: Results on the Full Whirlpool Compression Function, in: Advances in Cryptology–ASIACRYPT 2009, Springer, 2009, pp. 126–143.
- H. Gilbert, T. Peyrin, Super-sbox Cryptanalysis: Improved Attacks for AES-like Permutations, in: Fast Software Encryption, Springer, 2010, pp. 365–383.
- O. Dunkelman, N. Keller, A. Shamir, Improved Single-Key Attacks on 8-Round AES-192 and AES-256, in: Advances in Cryptology-ASIACRYPT 2010, Springer, 2010, pp. 158–176.
- F. Mendel, T. Peyrin, C. Rechberger, M. Schläffer, Improved Cryptanalysis of the Reduced Grøstl Compression Function, Echo Permutation and AES Block Cipher, in: Selected Areas in Cryptography, Springer, 2009, pp. 16–35.
- D. Khovratovich, I. Nikolić, C. Rechberger, Rotational Rebound Attacks on Reduced Skein, in: Advances in Cryptology-ASIACRYPT 2010, Springer, 2010, pp. 1–19.
- A. Duc, J. Guo, T. Peyrin, L. Wei, Unaligned Rebound Attack: Application to Keccak, in: Fast Software Encryption, Springer, 2012, pp. 402–421.
- A. Joux, Multicollisions in Iterated Hash Functions: Application to Cascaded Constructions, in: Advances in Cryptology–CRYPTO 2004, Springer, 2004, pp. 306–316.
- D. Wagner, A Generalized Birthday Problem, in: Advances in Cryptology–CRYPTO 2002, Springer, 2002, pp. 288–304.