
Шифр FEAL обладает таким же уровнем стойкости что и DES. Более того, увеличенная длина ключа (64 бита по сравнению с 56 битами в DES) затрудняет возможность перебора. Шифр FEAL обладает хорошим распределением шифротекстов, близким к случайному. И это тоже говорит в пользу FEAL по сравнению с DES.Это краткое содержание спецификации алгоритма шифрования FEAL, опубликованного в 1987 году.
Ничто не вечно под луной. В данном топике я расскажу как при наличии всего 40 пар открытых-закрытых текстов получить полный ключ FEAL4 за несколько минут.
Дифференциальный криптоанализ
Для начала разберемся что же скрывается под ласкающим русское ухо названием «Дифференциальный криптоанализ».
Дифференциальный криптоанализ — атака с подобранным открытым текстом. Это означает, что для применения ДК вы должны иметь возможность зашифровать абсолютно любые тексты в абсолютно любом количестве.
Целью атакующего, применяющего ДК, является получение некоторой информации о ключе, которая может как полностью скомпрометировать ключ (что бывает очень редко), так и просто дать некоторое преимущество при подборе ключа.
Работает это все следующим образом. Для двух заранее подобранных шифротекстов P1 и P2 злоумышленник вычисляется «дифференциал» ΔP=P1⊕P2. И с помощью ΔP пытается определить каким должен быть «дифференциал» шифротекстов ΔС=C1⊕C2. Зачастую невозможно предугадать со 100% точностью какое именно будет иметь значение ΔС. Единственное, что может злоумышленник, это определить с какой частотой шифр возвращает различные значения ΔС, для заданного заранее ΔP. Это знание позволяет атакующему вскрыть часть ключа или ключ целиком.
В качестве примера разберем трехраундовый блочный шифр, изображенный на рисунке ниже.
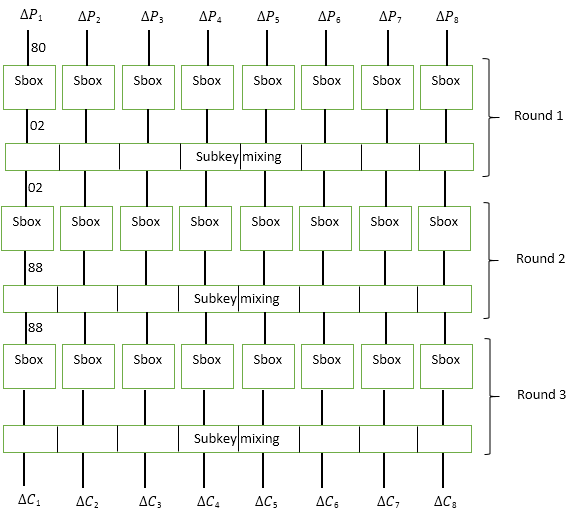
Данный шифр имеет 64 битный размер блока и 128 битный ключ.
На каждом раунде входной блок делится на 8 байт, каждый из которых проходит через функцию подстановки Sbox. После этого данные перемешиваются с 64 битным подключом Subkey. Функция перемешивания представляет собой обычный XOR.
Предположим, что злоумышленник решил проверить дифференциал 0x80. Для этого он генерирует произвольный байт X1, и вычисляет X2=X1⊕80.
Далее атакующий прогоняет X1 и X2 через функцию Sbox и получает значения Y1 и Y2. Для каждой такой пары X1 и X2, дифференциал которых равен 80, атакующий в состоянии получить дифференциал ΔY. Анализируя полученные значения, атакующий выбирает такое значение ΔY, которое имеет большую вероятность возникновения.
Возвращаясь к нашему примеру, предположим, что из всех 256 пар X1 и X2, в 192 случаях Y1⊕Y2=02. Таким образом, вероятность того, что при заданном ΔX=80, значение ΔY=02, составляет 192/256=3/4. Это в свою очередь означает, что при заданном ΔX=80, с вероятность P1=3/4 на вход второго раунда попадут два значения U1 и U2, такие что ΔU=02.
Обратите внимание, что ключ никоим образом не влияет на значение дифференциалов. Так как при шифровании разных текстов ключ не изменяется и перемешивание с ключевой последовательностью осуществляется с помощью XOR, то при вычислении ΔU байты ключа взаимно исключаются.
Для раскрытия свойств второго раунда, злоумышленник генерирует новые 256 пар входных байт X1 и X2, таких, что X1⊕X2=02. Произведя вычисление функции Sbox для каждой пары X1 и X2, атакующий замечает, что в 64 случаях из 256 ΔY=88. Т.е. вероятность того, что ΔY=88, для заданного ΔX=02, составляет P2=64/256=1/4.
Таким образом, произведя нехитрый подсчет вероятностей, атакующий понимает, что для указанного шифра для каждой пары байт X1 и X2, таких что ΔX=80, с вероятность P= P1*P2=3/4*1/4=3/16, дифференциал внутреннего состояния шифра перед последним раундом составляет ΔY=88.
Обладая этим знанием атакующий генерирует несколько пар текстов таких, что ΔP=808080808080 и приступает к побайтовому подбору подключа третьего раунда.
Покажем каким образом осуществляется вскрытие первого байта подключа.
Для каждого из 256 возможных вариантов первого байта Subkey[0] и для каждой пары шифротекстов {C1, C2}, злоумышленник вычисляет U1=Sbox(C1⊕Subkey[0]) и U2=Sbox(C2⊕Subkey[0]).
Если Subkey[0] угадан правильно, то приблизительно 3 из каждых 16 пар U1 и U2 при вычислении ΔU будут равны 88.
Подобрав таким образом наиболее вероятный первый байт подключа Subkey, атакующий может перейти ко второму байту и действуя аналогичным образом вскрыть весь ключ третьего раунда.
После того, как ключ последнего раунда будет раскрыт, злоумышленник может приступить к атаке на предпоследний раунд и действуя подобным образом в конечном итоге получит информацию о всех раундовых ключах шифра.
Описание шифра FEAL
Теперь рассмотрим криптоалгоритм с которым мы попытаемся совершить описанные выше действия.
Итак, FEAL4 это блочный шифр, с размером блока и длиной ключа равными 64 бита.
Существует несколько равноценных описаний алгоритма FEAL4, мы воспользуемся наиболее удобным для демонстрации дифференциального криптоан��лиза.

Шифр состоит из 4-х раундов и использует шесть 32-битных подключей, генерируемых из основного ключа(в дальнейшем будем считать, что каждый подключ генерируется независимо, «увеличив» таким образом порог стойкость с 264 до 2192).
На начальном этапе открытый текст разбивается на два блока, по 32 бита каждый. Левый и правый блоки складываются по модулю два с 32-битными подключами K[4] и K[5] соответственно. Затем левая часть остается без изменений, а правая образуется сложением по модулю два с левым блоком.
После этого выполняется 4 раунда шифрования на каждом из которых правый блок суммируется по модулю два с подключом раунда K[i], а затем полученный результат прогоняется через функцию перестановки F. Результат перестановки складывается с левой частью текста. После этих операций левый и правый блок меняют местами и полученный результат подается на вход следующего раунда.
Последний раунд немного отличается от всех остальных. Левые и правые блоки не меняются местами, как в предыдущих раундах.
Вместо этого, правый блок складывается по модулю два с левым блоком и полученный результат возвращается в качестве правой части шифротекста. Левая же часть после 4 раунда остается неизменной и составляет первые 32 бита полученного шифротекста.
Оригинальная схема шифра, описанная создателями несколько отличалась от приведенной выше. Вместо шести 32-битных, в оригинальном описании используются двенадцать 16-битных подключа. Однако, оба варианта идентичны и при желании 32-битные ключи можно легко представить в виде 16-битных ключей из оригинального описания.
Единственным белым пятном в описании шифра осталась функция F. На рисунке ее можно представить следующим образом:
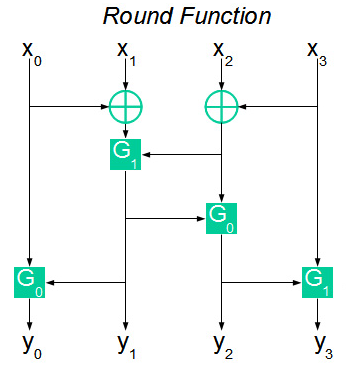
На входе функция F получает 4 байта X1, X2, X3, X4. Далее входные байты перемешиваются и проходят через функции G0 или G1. 4 байта полученных после вычисления функций Gx образуют 32-битную выходную последовательность функции F.
Функции G0 и G1 выполняют преобразование 16-битной входной последовательности в 8-битный результат.
Функцию G0 можно выразить следующим образом:
 , где << — циклический сдвиг влево.
, где << — циклический сдвиг влево.В то время как функция G1 имеет следующее определение:
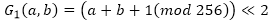 .
.Расшифровка алгоритма происходит по такому же самом принципу. Собственно, шифротекст разбивается на левый и правый блок и все операции шифрования выполняются в обратном порядке.
Т.е. сперва выполняется расшифровка последнего раунда, затем предпоследнего и так далее.
реализация FEAL4 на C#
class FEAL4 { private byte G0(byte a, byte b) { return (byte)((((a + b) % 256) << 2) | (((a + b) % 256) >> 6)); } private byte G1(byte a, byte b) { return (byte)((((a + b+1) % 256) << 2) | (((a + b+1) % 256) >> 6)); } public byte[] F(byte[] x) { byte[] y = new byte[4]; y[1] = G1((byte)(x[0] ^ x[1]), (byte)(x[2] ^ x[3])); y[0] = G0(x[0], y[1]); y[2] = G0(y[1], (byte)(x[2] ^ x[3])); y[3] = G1(y[2], x[3]); return y; } private void AddKeyPart(byte[] P, byte[] K) { for (int i = 0; i < 4; i++) { P[i] = (byte)(P[i] ^ K[i]); } } private byte[] XOR(byte[] a, byte[] b) { byte[] c=new byte[a.Length]; for (int i = 0; i < c.Length; i++) { c[i] = (byte)(a[i] ^ b[i]); } return c; } public byte[] Encrypt(byte[] P, byte[][] K) { byte[] LeftPart = new byte[4]; byte[] RightPart = new byte[4]; Array.Copy(P, 0, LeftPart, 0, 4); Array.Copy(P, 4, RightPart, 0, 4); AddKeyPart(LeftPart, K[4]); AddKeyPart(RightPart, K[5]); byte[] Round2Left = XOR(LeftPart, RightPart); byte[] Round2Right = XOR(LeftPart, F(XOR(Round2Left, K[0]))); byte[] Round3Left = Round2Right; byte[] Round3Right = XOR(Round2Left,F(XOR(Round2Right,K[1]))); byte[] Round4Left = Round3Right; byte[] Round4Right = XOR(Round3Left, F(XOR(Round3Right, K[2]))); byte[] CipherTextLeft = XOR(Round4Left,F(XOR(Round4Right,K[3]))); byte[] CipherTextRight = XOR(Round4Right, CipherTextLeft); byte[] CipherText = new byte[8]; Array.Copy(CipherTextLeft, 0, CipherText, 0, 4); Array.Copy(CipherTextRight, 0, CipherText, 4, 4); return CipherText; } public byte[] Decrypt(byte[] P, byte[][] K) { byte[] LeftPart = new byte[4]; byte[] RightPart = new byte[4]; Array.Copy(P, 0, LeftPart, 0, 4); Array.Copy(P, 4, RightPart, 0, 4); byte[] Round4Right = XOR(LeftPart, RightPart); byte[] Round4Left = XOR(LeftPart, F(XOR(Round4Right, K[3]))); byte[] Round3Right = Round4Left; byte[] Round3Left = XOR(Round4Right, F(XOR(Round3Right, K[2]))); byte[] Round2Right = Round3Left; byte[] Round2Left = XOR(Round3Right, F(XOR(Round2Right, K[1]))); byte[] Round1Right = Round2Left; byte[] Round1Left = XOR(Round2Right, F(XOR(Round1Right, K[0]))); byte[] TextLeft = Round1Left; byte[] TextRight = XOR(Round1Left,Round1Right); AddKeyPart(TextLeft, K[4]); AddKeyPart(TextRight, K[5]); byte[] Text = new byte[8]; Array.Copy(TextLeft, 0, Text, 0, 4); Array.Copy(TextRight, 0, Text, 4, 4); return Text; } }
Дифференциальный криптоанализ шифра FEAL4
Как и в приведенном выше примере начнем криптоанализ шифра с исследования функции подстановки F. Именно здесь скрыт самый значительный изъян всего шифра FEAL. Дело в том, что функция F обладает одним катастрофическим с точки зрения безопасности свойством. Любые два значения X1 и X2, такие что их дифференциал X1⊕X2=0x80800000, преобразуются в Y1 и Y2. При этом дифференциал Y1⊕Y2=0x02000000 в 100% случаев.
Для того, чтобы понять почему так происходит взглянем на преобразование дифференциалов, которое происходит при вычислении функции F.

Легко заметить, что ненулевое значение поступает на вход функции G, только в позиции первого байта. Соответственно на выходе получаем
 .
.Нетрудно понять, что это свойство делает шифр абсолютно уязвимым перед дифференциальным криптоанализом. 100% вероятность возникновения определенного дифференциала ΔY позволяет свести количество необходимых для атаки пар открытый-закрытый текст к минимуму.
Рассмотрим какие шаги следует предпринять злоумышленнику для вскрытия ключа последнего раунда K[3].
Атакующий генерирует несколько пар открытых текстов P1 и P2, таких что ΔP=0x8080000080800000. Зная, описанное выше свойство функции F, атакующий в состоянии рассчитать дифференциалы практически на каждом раунде шифрования.
Отследить поведение дифференциалов вы можете на следующей картинке:

Как видите дифференциалы просчитываются вплоть до последнего раунда. Но и без этого у атакующего уже достаточно информации, чтобы вскрыть последний раундовый ключ.
На иллюстрации ниже изображены два последних раунда шифра FEAL4.
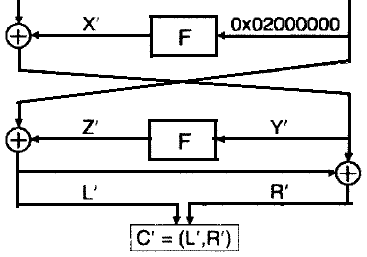
Обладая парой шифротекстов C1 и C2 атакующий может вычислить ΔC, получив таким образом значения L' и R'.
На основании этого он может вычислить Z'=L'⊕02.
C другой стороны для каждой пары шифротекстов C1 и C2, злоумышленник может вычислить Y1 и Y2.
Зная Y1 и Y2 атакующий начинает перебор ключа K[3]. Для каждого возможного ключа Kpos вычисляется Z1=F(Y1⊕Kpos) и Z2=F(Y2⊕Kpos). Сложив по модулю два значения Z1⊕Z2 атакующий сравнивает получившееся значение с предвычисленным заранее Z'. Если Z'=Z1⊕Z2, значит Kpos вероятнее всего и является искомым подключом K[3].
Для того, чтобы снизить вероятность ошибки полученный ключ Kpos необходимо проверить с несколькими парами шифротекстов(я в своей реализации использовал 10 пар).
Нетрудно посчитать, что атака, описанная выше, требует 232 вычислений функции F. Это конечно не 264, заявленные создателями шифра, но все равно цифра не очень приятная особенно если мы хотим вычислить все 4 раундовых ключа, а мы несомненно этого хотим.
К счастью атаку можно упростить и свести количество вычислений ко вполне комфортным 217.
Для этого введем определение функции
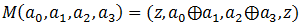 , где a — набор байт, и z — нулевой байт.
, где a — набор байт, и z — нулевой байт. Для каждого A=(z, a0, a1, z) злоумышленник вычисляет Q0=F(M(Y0)⊕A) и Q1=F(M(Y1)⊕A).
Нетрудно убедиться, что если A=M(K[3]), тогда второй и третий байт значения Q0⊕Q1 совпадут со вторым и третьим байтом значения Z'. Таким образом мы получаем информацию о двух байтах потенциального ключа Kpos.
После этого для всех значений b0 и b1, атакующий вычисляет последовательность Kpos=(b0, b0⊕a0, b1⊕a1, b1) и проверяет полученную последовательность описанным выше способом.
После вскрытия подключа K[3], злоумышленник способен восстановить значения в которых находился шифр после третьего раунда и это даст ему возможность атаковать аналогичным образом подключ K[2]. Здесь, правда, необходимо заметить, что для атаки на ключ K[2] необходимо будет использовать другой исходный дифференциал, т.к. дифференциал ΔP=0x8080000080800000 на втором раунде всегда ведет к значению Z'=0x02000000, при любом используемом ключе. И это не позволит угадать ключ второго раунда.
В качестве дифференциалов для вскрытия каждого из подключей можно использовать следующие значения:
Round 4: 0x8080000080800000
Round 3: 0x0000000080800000
Round 2: 0x0000000002000000
Round 1: 0x0200000080000000
После вскрытия всех четырех ключей каждого из раундов легко вычислить ключи K[5] и K[4] для этого достаточно прогнать любой шифротекст через 4 раунда расшифровки и получившееся значение сложить по модулю два с известным открытым текстом.
Есл�� интересно скачать исходники атаки вы можете здесь.
