В последнее время на Хабре появилось множество статей о нейронных сетях. Из них очень интересными показались статьи о Перцептроне Розенблатта: Перцептрон Розенблатта — что забыто и придумано историей? и Какова роль первого «случайного» слоя в перцептроне Розенблатта. В них, как и во многих других очень много написано о том, что сети справляются с решением задач, и обобщают до некоторой степени свои знания. Но хотелось бы как-то визуализировать эти обобщения и процесс решения. Увидеть на практике, чему там научился перцептрон, и почувствовать, насколько успешно ему это удалось. Возможно, испытать горькую иронию относительно достижения человечества в области ИИ.Языком у нас будет С#, только потому что я недавно решил его выучить. Я разобрал два наиболее простых примера: однослойный перцептрон Розенблатта, обучаемый коррекцией ошибки, и многослойный перцептрон Румельхарта, обучаемый методом обратного распространения ошибки. Для тех, кому, как и мне, стало интересно, чему они там на самом деле обучились, и насколько они на самом деле способны обобщать – добро пожаловать под кат.
ОСТОРОЖНО! Много картинок. Куски кода.
Для начала хочу предложить вам полюбоваться процессом обучения нейронной сети. Каждый кадр после 1000 учебных точек. Указывается скорость обучения и среднеквадратичная ошибка за эту тысячу циклов.
Из кода я буду показывать только то, что может пригодиться другим желающим сделать всё своими руками или проверить правильность моих выводов. Код важных элементов с корнем выдирается из тестового проекта, в котором он запускался, поэтому где-то могут быть ссылки на элементы, которые я не привожу. Но код при этом работающий, все картинки являются скриншотами из моего учебного проекта.
Для начала нужно выбрать задачу, такую, чтобы на неё глянул, и сразу стало понятно, научился ли перцептрон чему-нибудь и чему. Возьмём две координаты (x и y), и накидаем в них много случайных точек. Это будут входные данные. Нарисуем какой-нибудь график и попросим перцептрон определить, находится точка выше или ниже этого графика. Но перцептрон Розенблатта же у нас работает в целых числах, да и вообще задачка слишком простая. Тогда давайте каждую координату округлим до целого числа и представим в двоичной форме: одна цифра-один вход. Для единообразия во всех примерах рассматривается диапазон координат (0,1), так что перед округлением его надо помножить на максимальное целое значение.
Например, представим каждую координату двухбитным числом. Пара случайных чисел (0.2, 0.7), указывающих на точку выше графика, тогда после округления перейдёт в (1,3) и даст нам следующий учебный пример:
new double[]{0.2, 0.7} => new NeuralTask {
Preview = new double[]{0.25, 0,75, 1},
Input=new double[] {0,1,1,1},
Output=new double[]{1}}
Функция, конвертирующая случайные числа в учебные примеры, выглядит примерно так:
Функция конверсии
var Convertion = (double[] random, double value) => {
var input = new double[]{Math.Floor(random [0]*0x4)/0x4, Math.Floor(random [1]*0x4)/0x4},
byte x = (byte)(input[0] * 4);
byte y = (byte)(input[1] * 4);
int res = (y > value * 4 ? 1 : 0);
return new NeuralTask() {
input = new double[4]{
(x&2)>>1, x&1,
(y&2)>>1, y&1},
output = new double[1] { res },
preview = new double[3] { input[0], input[1], res }
};
};
Тут надо пояснить, что всё это делалось в учебных и исследовательских целях, поэтому не оптимизировалось для скорости и неземной красоты, а где-то писалось так, чтобы удобно было программировать любой мыслимый перцептрон. Поэтому, в частности, входные и выходные данные лежат в double. Получается такая вот простая картинка. Ну, или чуть более сложная, если каждую ось порубить на 256 участков, и функцию взять посложнее:
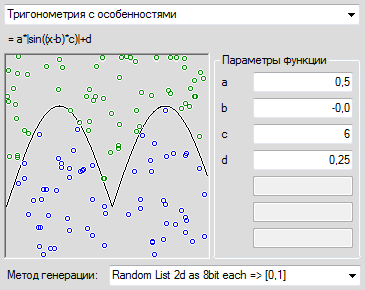
Здесь и далее зелёный цвет – значения больше нуля, тем более насыщенные, чем больше число, красные – значения меньше нуля, синий – значения равные 0 и их ближайшие окрестности.
Исходный код
Сам перцептрон у нас состоит из синапса:
Ничего неожиданного, если не считать, что числа хранятся в double и вместо стандартного события используется кастомное. Теперь нейрон. Нейроны у нас все дружно соответствуют интерфейсу IAxon:
Тоже ничего неожиданного, кроме Position, показывающего, где нейрон рисовать.
В качестве входа используются сенсорные нейроны, которым можно задавать значение напрямую:
Наконец, сам нейрон в достаточно обобщённой форме:
Здесь:
Наконец из всего этого вместе получается нейронная сеть и алгоритм её обучения:
Источник данных является
class Synaps
public class Synaps {
private double weight;
/// <summary>Доступатор к одному параметру</summary>
virtual public double Weight {
get { return weight; }
set {
if (weight != value) {
weight = value;
if (axon != null)
ChangeActionPotentialHandler(axon.ActionPotential);
}
}
}
/// <summary>Внутреннее хранилище ссылки на аксон. Возможно, в будущем, в целях оптимизации, разрешим из него читать наследникам, но писать в него точно нельзя.</summary>
private IAxon axon;
// Указание на нейрон, с которого снимается информация.
public IAxon Axon {
get { return axon; }
set { // Вот тут навешиваем обработчики, которые следят за изменением состояния исходного нейрона.
if (axon != null)
axon.RemoveChangeActionPotentialHandler(ChangeActionPotentialHandler);
axon = value;
if (axon != null) {
axon.AddChangeActionPotentialHandler(ChangeActionPotentialHandler);
ChangeActionPotentialHandler(axon.ActionPotential);
}
}
}
public double ActionPotential;
/// <summary> Событие кидается, когда синапс меняет свой потенциал.</summary>
protected Action WhenActionPotentialСhanged;
public void AddActionPotentialChangeHandler(Action handler) {
WhenActionPotentialСhanged += handler;
}
public void RemoveActionPotentialChangeHandler(Action handler) {
WhenActionPotentialСhanged -= handler;
}
virtual protected void ChangeActionPotentialHandler(double axonActionPotential) {
ActionPotential = axonActionPotential * weight; // Проверку на неизменность значения не делаю, потому что она уже есть в нейроне.
if (WhenActionPotentialСhanged != null)
WhenActionPotentialСhanged); // Просто передать событие об изменении потенциала на изучаемом нейроне
}
}
Ничего неожиданного, если не считать, что числа хранятся в double и вместо стандартного события используется кастомное. Теперь нейрон. Нейроны у нас все дружно соответствуют интерфейсу IAxon:
interface IAxon
public interface IAxon {
/// <summary>Значение потенциала действия.</summary>
double ActionPotential { get; }
/// <summary>Более успешной оптимизации не просматривается.</summary>
void AddChangeActionPotentialHandler(Action<double> handler);
void RemoveChangeActionPotentialHandler(Action<double> handler);
/// <summary>Положение, в котором находится аксон в пространстве нейронной сети.</summary>
PointF Position { get; set; }
/// <summary>Имя аксона чтобы идентифицировать его в трейсе.</summary>
string Name { get; set; }
}
Тоже ничего неожиданного, кроме Position, показывающего, где нейрон рисовать.
В качестве входа используются сенсорные нейроны, которым можно задавать значение напрямую:
class SensoryNeuron
public class SensoryNeuron : IAxon {
protected double actionPotential;
public double ActionPotential {
get { return actionPotential; }
set {
if (actionPotential != value) {
actionPotential = value;
if (WhenChangeActionPotential != null)
WhenChangeActionPotential(actionPotential);
}
}
}
}
Наконец, сам нейрон в достаточно обобщённой форме:
class Neuron
/// <summary>Общий предок. Есть только функция активации </summary>
public class Neuron : IAxon {
/// <summary> Список синапсов, с которых получает информацию этот нейрон. Список в виде массива, потому что перебирать массив быстрее, а изменение списка делается редко.</summary>
public Synaps[] Synapses = new Synaps[0];
/// <summary> Внутренний флаг, означающий, что один из синапсов поменял свой потенциал и нейрон нуждается в пересчёте.</summary>
protected bool synapsPotentialChanged = false;
/// <summary> Добавить в нейрон новую синаптическую связь. И нацепить, кроме того, все положенные слушатели. </summary>
public void AppendSinaps(Synaps target) {
// При каждом обновлении пересоздаём массив. Выглядит это, конечно, неоптимально, но эта операция делается очень редко, в отличии от самого вычисления.
Synapses = Synapses.Concat(new Synaps[1] { target }).ToArray();
target.AddActionPotentialChangeHandler(ChangeSynapsPotentialHandler); // Слушатели новые навешать.
synapsPotentialChanged = true;
}
virtual protected void ChangeSynapsPotentialHandler() {
synapsPotentialChanged = true;
}
/// <summary> Функция активации нейрона. Она тут хранится отдельной переменной, чтобы ускорить процесс вызова.</summary>
protected DTransferFunction transferFunctionDelegate;
public virtual DTransferFunction TransferFunction {
get { return transferFunctionDelegate; }
set {
transferFunctionDelegate = value;
}
}
/// <summary> Метод вызывает расчёт в нейроне и может привести к изменению его потенциала действия. </summary>
public virtual void Excitation() {
if (!synapsPotentialChanged) return; // Для нецелочисленного нейрона проверка почти всегда бессмысленна
synapsPotentialChanged = false;
synapsPotentials = 0;
for (int i = 0; i < Synapses.Length; i++)
synapsPotentials += Synapses[i].ActionPotential;
double newValue = transferFunctionDelegate(synapsPotentials);
if (actionPotential != newValue) { // Для некоторых специальных случаев значения могут не отличаться. Например, для целочисленного перцептрона.
actionPotential = newValue;
if (WhenChangeActionPotential != null)
WhenChangeActionPotential(actionPotential);
}
}
}
Здесь:
Функция Активации
/// <summary> Функция определения потенциала действия на основе входных сигналов. </summary>
/// <param name="argument">Сумма потенциалов синапсов</param>
/// <returns>Возвращает значение потенциала действия нейрона</returns>
public delegate double DTransferFunction(double argument);
DTransferFunction BarrierTransferFunction = (double x) => x <= 0 ? 0 : 1;
Наконец из всего этого вместе получается нейронная сеть и алгоритм её обучения:
class NeuralNetwork, PerceptronClassic, ErrorCorrection
abstract public class NeuralNetwork {
/// <summary>Вход нейронной сети</summary>
public SensoryNeuron[] Input = new SensoryNeuron[0];
/// <summary>
/// Все добавленыне в сеть нейроны выстраиваются в этом массиве в том порядке, в котором будут обработаны. Сенсорные нейроны сюда вообще не попадают.
/// Я не закладываю заранее послойность или любой другой предопределённый алгоритм обхода, чтобы конкретная реализация сети могла переопределять порядок обработки по вкусу.
/// </summary>
public Neuron[] ExcitationOrder = new Neuron[0];
/// <summary>Выход нейронной сети</summary>
public Neuron[] Output = new Neuron[0];
/// <summary>Универсальный метод, создающий сеть с указанными в классе параметрами</summary>
/// <param name="input">Количество сенсорных нейронов - входов</param>
/// <param name="output">Количество выходных нейронов реакции</param>
abstract public void create(uint input, uint output);
public void execute(double[] data) {
// Несовпадение размерности входных сигналов и входа сети на данном этапе не проверяем для экономии
for (int i = 0; i < Input.Length && i < data.Length; i++) {
Input[i].ActionPotential = data[i];
}
for (int i = 0; i < ExcitationOrder.Length; i++)
ExcitationOrder[i].Excitation();
}
public double[] Result() {
// return output.Select(s => s.ActionPotential).ToArray(); //TODO Не забыть сравнить с Linq по скорости.
double[] res = new double[Output.Length];
for (int i = 0; i < res.Length; i++)
res[i] = Output[i].ActionPotential;
return res;
}
}
public class PerceptronClassic : NeuralNetwork {
// Насколько в слое больше нейронов, чем входов сети
public int neuronCountsOverSensoric = 15;
//Сколько синапсов у каждого нейрона
public int ANeuronSynapsCount;
// Первый слой нейронов линейного разложения
public Neuron[] Layer;
// Класс собирает перцептрон Ролзенблатта по заданным характеристикам
override public void create(uint inputCount, uint outputCount) {
rnd = rndSeed >= 0 ? new Random(rndSeed) : new Random();
// Сенсорные нейроны
this.Input = new SensoryNeuron[inputCount];
for (int i = 0; i < inputCount; i++)
Input[i] = new SensoryNeuron() {Name = "S" + i};
//Группа нейронов первого слоя - Ассоциативные
Layer = new Neuron[inputCount + neuronCountsOverSensoric];
for (int i = 0; i < Layer.Length; i++) {
// Это сам нейрон
Layer[i] = new RosenblattNeuron();
// А это его случайные необучаемые синапсы первого слоя
SensoryNeuron[] sub = Input.OrderBy((cell) => rnd.NextDouble()).Take(ANeuronSynapsCount).ToArray();
// Их не больше, чем входных сигналов
for (int j = 0; j < sub.Length; j++) {
Synaps s = new Synaps();
s.Axon = sub[j];
s.Weight = rnd.Next(2) * 2 - 1;
Layer[i].AppendSinaps(s);
}
}
// Назвать сообразно месту в системе.
for (int i = 0; i < Layer.Length; i++)
Layer[i].Name = "A" + i;
// Выходные нейроны - Реагирующие элементы
Output = new Neuron[outputCount];
for (int i = 0; i < Output.Length; i++) {
Output[i] = new RosenblattNeuron();
Output[i].Name = "R" + i;
// Их синапсы с каждым из предыдущего слоя
for (int j = 0; j < Layer.Length; j++) {
Synaps s = new Synaps();
s.Axon = Layer[j];
Output[i].AppendSinaps(s); // Начальный вес 0
}
}
// И складываем в кучу обсчитываемых нейронов
int lastIndex = 0;
ExcitationOrder = new Neuron[Layer.Length + Output.Length];
foreach (Neuron cell in Layer)
ExcitationOrder[lastIndex++] = cell;
foreach (Neuron cell in Output)
ExcitationOrder[lastIndex++] = cell;
}
}
/// <summary>Алгоритм обучения коррекцией ошибки.</summary>
public class ErrorCorrection : LearningAlgorythm {
// Метод, описывающий одиночный акт обучения на одном примере
override protected double LearnNet(double[] required) {
double error = 0;
for (int i = 0; i < required.Length && i < net.Output.Length; i++) {
if (required[i] != net.Output[i].ActionPotential) {
error += 1;
// Перебираем все ассоциативные нейроны
for (int j = 0; j < (net as PerceptronClassic).Layer.Length; j++)
// Находим тех из них, кто активировался
if ((net as PerceptronClassic).Layer[j].ActionPotential > 0)
// У всех нейронов второго слоя
foreach (RosenblattNeuron cell in net.Output)
// Изменяем веса всех синапсов, которые указывают на активированный ассоциативный нейрон
// Если правильное решение – дезактивация, то снижаем вес, если активация – повышаем. Вес может стать отрицательным.
cell.Synapses[j].Weight += required[i] <= 0 ? -1 : 1;
}
}
return error;
}
/// <summary>Обучает одному набору от начала и до конца</summary>
public void LearnTasksSet() {
if (data == null) { Console.WriteLine("Источник данных отсутствует"); return; }
data.Reset();
LearnedTaskSetsCount++;
ErrorsInSet = LearnedTasksInSetCount = 0;
int max = 1000;
while (data.MoveNext() && --max >= 0)
LearnCurrentTask();
// На выходе сет не переключается, поэтому статистика остается видна.
}
/// <summary>Обучать всему сету несколько раз или пока сеть не научится.</summary>
/// <param name="loops">Сколько раз прогнать учебный сет</param>
public void LearnSetManyTimesUntilSuccess(int loops) {
for (int i = 0; i < loops; i++) {
LearnTasksSet();
if (ErrorsInSet == 0) {
break;
}
}
}
}
Источник данных является
Enumerable<NeuralTask> и при каждом Reset-е переставляет точки в последовательности в произвольном порядке.Всё готово, можно запускать.
Для простейшей задачки по два бита на ось, чтобы нам повезло найти подходящее сепарабельное разложение, пришлось добавить в слой A на 8 нейронов больше, чем входов – 12 штук. Подходящее разложение обнаружилось с третьей попытки. Перцептрон безошибочно классифицировал все 16 возможных значений.
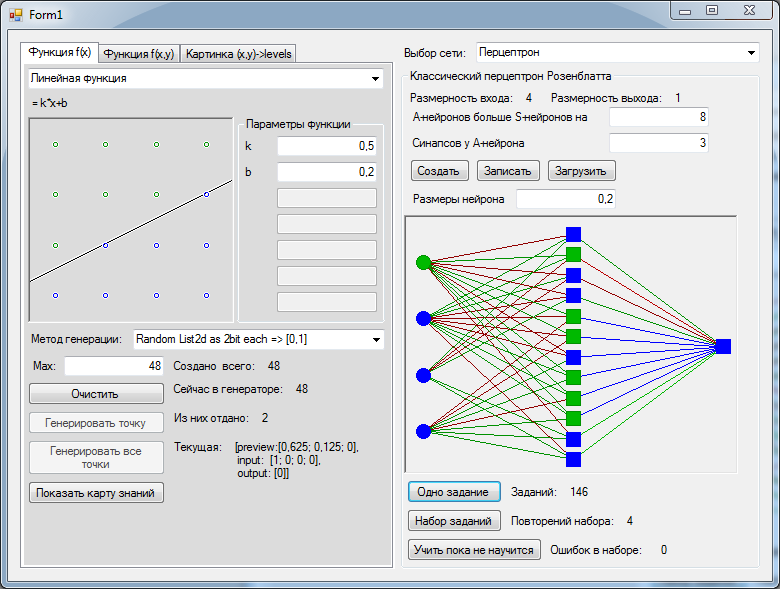
Тут можно заметить, что возможных значений всего 16, а я сгенерировал больше. Чтобы случайные числа гарантированно покрыли все возможные варианты.
Раз всё так замечательно, давайте перейдём к чуть более сложной задачке, где на каждую ось у нас приходится 256 вариантов значений. Функцию рассмотрим простейшую. Сгенерируем, для начала, 64 точки. В слое нейронов всего на 20 больше, чем входов – 36 штук. И сразу же успех.
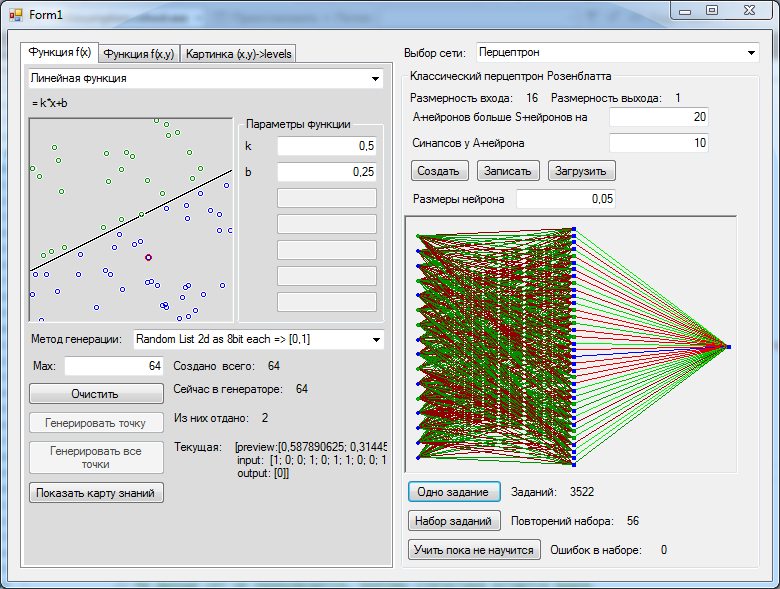
И вот теперь мы сделаем самое интересное. Мы возьмём полученную нами сеть и нарисуем на картинке все возможные значения, которые выдаёт сеть во всех точках. И вот тут выяснится самое грустное. Уровень обобщения, достигнутый сетью, не очень то впечатляет.
Оказывается, сеть в весьма общих чертах представляет, какая закономерность скрывается за предоставленными ей точками. Попробуем предоставить сети более полные данные об изучаемой функции. Сгенерируем 256 точек. 36-ти нейронов, как в прошлый раз, уже недостаточно, чтобы сеть смогла натолкнуться на подходящее линейно сепарабельное разложение. Теперь нам потребовалось создать 70 ассоциативных нейронов, прогнать учебный набор задач 615 раз и пропылесосить кулер, чтобы процессор не перегревался от радости всего за одну секунду обучения. Обобщение, достигнутое сетью, стало лучше, но невооружённым взглядом видно, что полученное улучшение несоразмерно затраченным усилиям.
В сердцах, мы покрываем пространство 2048 точками. Вынужденно создаём уже 266 нейронов в ассоциативном слое, подбираем оптимальное количество синапсов на нейрон (получается 8) учим набор 411 раз (пока сеть не перестанет ошибаться) и смотрим на достигнутый результат.
Не знаю, как вы, а я что-то не вижу качественного улучшения. Сеть исправно зазубривает все значения наизусть, ни в малой степени не приближаясь к обобщению предложенной ей закономерности. Да и вообще видно, что характер сделанных сетью глубокомысленных выводов не так уж и сильно зависит от характера стоящей перед ней задачи.
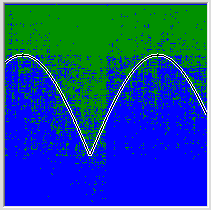
Спасибо, конечно, что сумела хотя бы это выучить. Похоже на то, что теоремы верны, и если я располагаю достаточным количеством нейронов, то смогу заставить сеть заучить хоть все возможные для данной задачи 65536 вариантов, но на это нам потребуется примерно 1500-2000 нейронов и водяное охлаждение. Чтобы запомнить всю информацию, содержащуюся в такой сети, нам потребуется на каждый синапс по 5 бит (4 бита на номер аксона и бит веса), на каждый нейрон 16 бит на значение веса аксона и 40 бит на все синапсы. А один обучающий пример весит 17 бит. В нашем примере с 2048 точками получается, что обучающая информация весит всего в два раза больше, чем информация о полученной сети.
Удобные задачи
Так в чём же проблема? В чём причина такой безрадостной картины? Давайте попробуем решить задачу аналитически. Допустим, у нас есть перцептрон, но только веса первого слоя, также как и второго, поддаются обучению. Во втором слое у нас всего лишь три нейрона. Первый связан с первыми 8 входами и имеет не барьерную, а просто линейную функцию активации. Второй нейрон такой же, но только отвечает за преобразование вторых 8 битов в обычные координаты. Третий связан со всеми, имеет барьерную функцию и призван давать 1, если хотя бы на одном входе есть хотя бы что-то. В следующем слое два из нейронов суммируются, опять без барьерной функции, но с очень важными весовыми коэффициентами, отражающими параметры функции. И, наконец, последний нейрон будет сравнивать два входных сигнала. Просто, логично и ни капли не интересно. Вместе с тем это почти минимально возможное количество задействованных нейронов и синапсов для данной задачи. А вот теперь попробуйте представить, сколько нейронов нужно, чтобы любую из этих операций выразить в однослойном перцептроне, у которого веса синапсов в первом слое могут быть только -1 и 1. Например, приведение 8 бит к одному числу. Я вам подскажу – нужно примерно 512 штук нейронов, и это мы ещё сравнивать не начинали.То есть проблема не в том, что перцептрон Розенблатта не может выучиться этому набору данных. Проблема в том, что делать ему это очень и очень неудобно. Кто дружен с теоремой больших чисел, может попробовать прикинуть, какова вероятность встретить подходящее для этого линейно-сепарабельное разложение. Перцептрону Розенблатта удобно решать задачи, хорошо представимые в виде пятнистого сине-зелёного размытого градиента, но всё становится грустно, когда это не так.
А что с многослойным перцептроном Румельхарта?
А что если проблемы только у однослойного перцептрона Розенблатта, а у многосложного перцептрона, обучаемого методом обратного распространения ошибки всё будет очень хорошо, и даже волшебно? Давайте же попробуем.
Исходный код
Во-первых, теперь у нас добавится функция вычисления первой производной от функции активации нейрона при текущих значениях. Всё это можно страшно оптимизировать и синлайнить вычисление производной прямо в формулу, в которой она будет применяться, но наша задача же не в том чтобы всё ускорить, а в том, чтобы разобратся как оно работает. Поэтому отдельная функция:
В качестве сигмоиды воспользуемся, например, Гипертангенсом:
Теперь сам нейрон. Он отличается только тем, что при каждом вычислении значения рассчитывает также производную от него по сумме входных сигналов, и наличием переменной, в которой будет храниться значение, используемое для обратного распространения ошибки.
Мне, последнее время, нравится использовать LINQ, потому что так проще и быстрее писать экспериментальный код. Для удобства этого дела моя маленькая домашняя функция, расширяющая его возможности. Использую её вместо List.ForEach чтобы вызов был красивый и однострочный.
Сам перцептрон.
И, наконец, алгоритм обучения. Целиком написан на LINQ потому что так было быстрее написать, и проще редактировать. Да, я знаю, что работает медленнее.
Производная от функции активации
/// <summary> Функция определения производной от потенциала действия. </summary>
/// <param name="argument">Сумма потенциалов синапсов</param>
/// <param name="funcResult">Потенциал действия нейрона, посчитанный для данных значений</param>
/// <returns>Возвращает значение производной потенциала действия в данной точке.</returns>
public delegate double DTransferFunctionDerivative(double argument, double funcResult);
В качестве сигмоиды воспользуемся, например, Гипертангенсом:
DTransferFunction Function = (x) => Math.Tanh(x),
DTransferFunctionDerivative Derivative = (x, th) => (1 - th) * (1 + th)
Теперь сам нейрон. Он отличается только тем, что при каждом вычислении значения рассчитывает также производную от него по сумме входных сигналов, и наличием переменной, в которой будет храниться значение, используемое для обратного распространения ошибки.
class NeuronWithDerivative
public class NeuronWithDerivative : Neuron {
/// <summary> Производная функции активации нейрона. Она тут хранится отдельно от своего класса чтобы ускорить процесс вызова.</summary>
protected DTransferFunctionDerivative transferFunctionDerivativeDelegate;
/// <summary></summary>
override public DTransferFunctionDerivative TransferFunction {
get { return transferFunctionDerivativeDelegate; }
set { transferFunctionDerivativeDelegate = value; }
}
/// <summary>Хранилище для предвычисленного значения первой производной от функции передачи</summary>
protected double actionPotentialDerivative = 0;
/// <summary>Первая производная от передаточной функции по её основному параметру.</summary>
public double ActionPotentialDerivative { get { return actionPotentialDerivative; } }
/// <summary>Параметр для расчёта обратного распостранения ошибки. Ну, или обратного распостранения производной. Кому как удобнее.</summary>
public double BackProprigationParametr = 0;
public override void Excitation() {
base.Excitation();
actionPotentialDerivative = transferFunctionDerivativeDelegate(synapsPotentials, actionPotential);
}
}
Мне, последнее время, нравится использовать LINQ, потому что так проще и быстрее писать экспериментальный код. Для удобства этого дела моя маленькая домашняя функция, расширяющая его возможности. Использую её вместо List.ForEach чтобы вызов был красивый и однострочный.
static class Tools
static class Tools {
/// <summary>Вызвать делегата в отношении каждого экземпляра в последовательности любого типа.</summary>
/// <param name="source">Перечислитель с исходными данными.</param>
/// <param name="func">Делегат, который надо вызывать.</param>
public static void Each<SequenceType>(this IEnumerator<SequenceType> source, Action<SequenceType> func) {
while (source.MoveNext())
func(source.Current);
}
/// <summary>Вызвать делегата в отношении каждого экземпляра в последовательности любого типа и передать ему индекс.</summary>
/// <param name="source">Перечислитель с исходными данными.</param>
/// <param name="func">Делегат, который надо вызывать. Второй параметр передаваемый делегату - индекс в последовательности. Отсчёт начинается со следующего элемента последовательности. В нетронутой - с начала.</param>
public static void Each<SequenceType>(this IEnumerator<SequenceType> source, Action<SequenceType, int> func) {
for (int i = 0; source.MoveNext(); i++)
func(source.Current, i);
}
/// <summary>Вызвать делегата в отношении каждого экземпляра в последовательности любого типа.</summary>
/// <param name="source">Перечислитель с исходными данными.</param>
/// <param name="func">Делегат, который надо вызывать.</param>
public static void Each<SequenceType>(this IEnumerable<SequenceType> source, Action<SequenceType> func) {
source.GetEnumerator().Each(func);
}
/// <summary>Вызвать делегата в отношении каждого экземпляра в последовательности любого типа и передать ему индекс.</summary>
/// <param name="source">Перечислитель с исходными данными.</param>
/// <param name="func">Делегат, который надо вызывать. Второй параметр передаваемый делегату - индекс в последовательности. Отсчёт начинается со следующего элемента последовательности. В нетронутой - с начала.</param>
public static void Each<SequenceType>(this IEnumerable<SequenceType> source, Action<SequenceType, int> func) {
source.GetEnumerator().Each(func);
}
}
Сам перцептрон.
class RumelhartPerceptron
// Многослойный перцептрон из обычных сравнительно быстрых нейронов с первой производной.
public class RumelhartPerceptron : NeuralNetwork {
/// <summary> Функция назначаемая нейронам. Задаётся извне.</summary>
DTransferFunctionDerivative TransferFunctionDerivative;
/// <summary>Количество нейронов в сети послойно, не считая сенсорного и выходного слоёв</summary>
public int[] NeuronsCount = new int[0];
override public void create(uint input, uint output) {
// Сенсорные нейроны.
Input = (new SensoryNeuron[input]).Select((empty, index) => new SensoryNeuron(){Name = "S[" + index + "]"}).ToArray();
// Фабрика всех остальных нейронов
Func<string, NeuronWithDerivative> create = (name) => {
NeuronWithDerivative neuron = new NeuronWithDerivative();
neuron.Name = name;
neuron.TransferFunction = TransferFunction;
neuron.TransferFunctionDerivative = TransferFunctionDerivative;
return neuron;
};
Func<IAxon, Synaps> createSynaps = (axon) => { Synaps s = new Synaps(); s.Axon = axon; return s; };
/// <summary>Нейроны внутренних слоёв</summary>
// Составим двумерный массив с нейронами слоёв
NeuronWithDerivative[][] Layers = NeuronsCount.Select((count, layer) => Enumerable.Range(0, count).Select(index => create("A[" + layer + "][" + index + "]")).ToArray()).ToArray();
// Создаём одномерный массив выходных нейронов
// Выходной слой
Output = Enumerable.Range(0, (int)output).Select(index => create("R[" + index + "]")).ToArray();
// Всем нейронам первого слоя навесить связи со слоем сенсоров.
Layers[0].Each(neuron => { Input.Select(createSynaps).Each(synaps => { neuron.AppendSinaps(synaps); }); });
// Всем нейронам, начиная со второго слоя, связи со всеми нейронами предыдущего слоя.
Layers.Skip(1).Each((layer, layerIndex) => { layer.Each(neuron => { Layers[layerIndex].Select(createSynaps).Each(synaps => { neuron.AppendSinaps(synaps); }); }); });
// Всем выходным нейронам выдать связи на нейроны
Output.Each(neuron => { Layers.Last().Select(createSynaps).Each(synaps => { neuron.AppendSinaps(synaps); }); });
// Сваливаем всё в очередь выполнения
ExcitationOrder = Layers.SelectMany(layer => layer).Concat(Output).ToArray();
// Рандомизируем веса синапсов в диапазоне от -1 до +1
Random rnd = new Random();
ExcitationOrder.Each(neuron => neuron.Synapses.Each(synaps => synaps.Weight = rnd.NextDouble() * 2 - 1));
}
}
И, наконец, алгоритм обучения. Целиком написан на LINQ потому что так было быстрее написать, и проще редактировать. Да, я знаю, что работает медленнее.
class BackPropagationLearning
public class BackPropagationLearning : LearningAlgorythm {
// Скорость, с которой происходит обучение
public double LearningSpeed = 0.01;
override protected double LearnNet(double[] required) {
double[] errors = net.Output.Select((neuron, index) => neuron.ActionPotential - required[index]).ToArray();
// Почистить все переменные обратного распостранения. Это позволит суммировать обратные переменные, обходя синапсы в порядке их присутствия в нейроне и не создавая двухсвязного списка связей в сети.
net.ExcitationOrder.Cast<NeuronWithDerivative>().Each(neuron => { neuron.BackProprigationParametr = 0; });
// В переменной BackProprigationParametr мы теперь храним dE/dS[i] = dE/dO[i] * F'[i](S[i])
// Для выходных нейронов производная от ошибки зависит от желаемых значений. BP[i] = dE/dO[i] * F'[i] = 2*(O[i]-T[i])*F'[i];
net.Output.Cast<NeuronWithDerivative>().Each((neuron, index) => { neuron.BackProprigationParametr = 2 * errors[index] * neuron.ActionPotentialDerivative; });
// Для всех синапсов посчитать долю производной, которую они внесли в свои аксоны BP[j] = SUM( dE/dO[i] * F'[i] * W[j,i] ) * F'[j] = SUM ( BP[i] * W[j,i] * F'[j])
net.ExcitationOrder.Reverse().Cast<NeuronWithDerivative>().Each(neuron => {
neuron.Synapses.SkipWhile(synaps => !(synaps.Axon is NeuronWithDerivative)).Each(synaps => {
(synaps.Axon as NeuronWithDerivative).BackProprigationParametr += neuron.BackProprigationParametr * (synaps.Axon as NeuronWithDerivative).ActionPotentialDerivative * synaps.Weight;
});
});
// А теперь меняем все веса, до которых дотягиваемся delta W[i,j] = -speed * dE/dS[j] * X[i];
net.ExcitationOrder.Reverse().Cast<NeuronWithDerivative>().Each(neuron => {
neuron.Synapses.Each(synaps => {
synaps.Weight += -LearningSpeed * neuron.BackProprigationParametr * synaps.Axon.ActionPotential;
});
});
// И возвращаем средний квадрат ошибки. (Усреднят и возьмут корень из него потом вышестоящие инстанции, для логов).
return errors.Select(e => e * e).Average();
}
public void LearnSomeTime(int sek) {
DateTime begin = DateTime.Now;
while (TimeSpan.FromTicks(DateTime.Now.Ticks - begin.Ticks).Seconds < sek) {
LearnTasksSet();
}
}
}
Вот такой вот код. От самой канонической реализации отличается лишь тем, что скорость обучения не зашита в обратно распространяемую ошибку, а умножается на изменение веса непосредственно перед применением. Минимизируем сумму квадратов ошибок, как учит нас википедия, заполнявшаяся в этой части хабровчанами.
Какую задачу подсунем нашей сети для начала? Давайте возьмём те же самые x и y с участка [0,1], В точках, которые выше графика, будем ожидать появления на выходе сети +1, в точках ниже графика -1. Кроме того мы сделаем не одну фиксированную последовательность учебных примеров, а будем создавать новый учебный пример каждый раз заново, чтобы нельзя было сказать, что у сети не было информации о каком-то важном участке пространства. Отдаём созданные пачки переменных по 1000 штук за сет. В превью показывается не одна точка, а несколько последних созданных только для красоты. Получается как-то так.
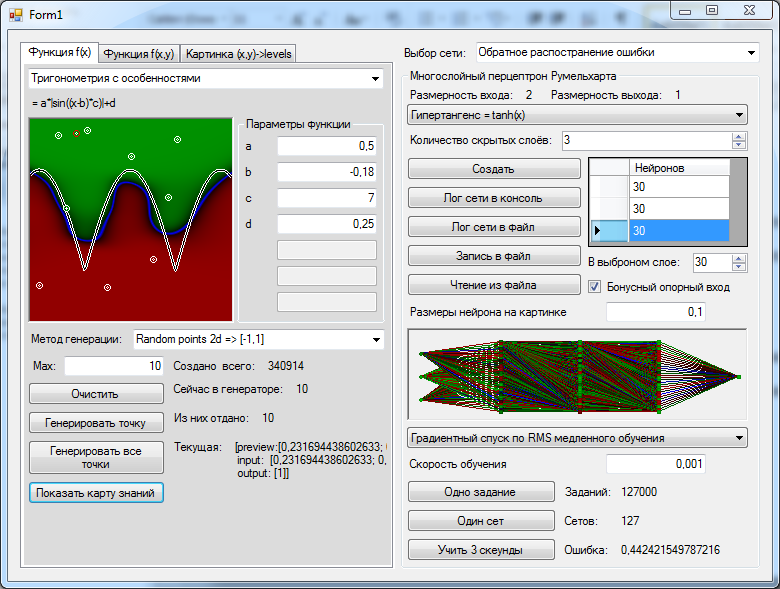
Создадим нейронную сеть. Википедия нам подсказывает, что трёх слоёв должно быть достаточно. Чтобы не показалось мало, нафигачим по 30 нейронов в слой.Попробуем учить некоторым подобием алгоритма имитации отжига, постепенно вручную уменьшая скорость обучения, по мере того, как среднеквадратичная ошибка за последние 1000 обучающих примеров перестаёт улучшаться. Программировать отжиг было лень, потому что моя статья не про это. Обучаем-обучаем, и наконец, когда качество сети перестают улучшаться рисуем на картинке значения, которые сеть выдаст для каждой из наших точек в квадрате 1x1.
Ну как по мне так довольно скромный результат, а это ещё и лучший из 5 попыток, у него хотя бы есть две вогнутости, это удаётся сети таких размеров не всегда. Обратите внимание на картинку с результатами ещё 4 попыток подряд.
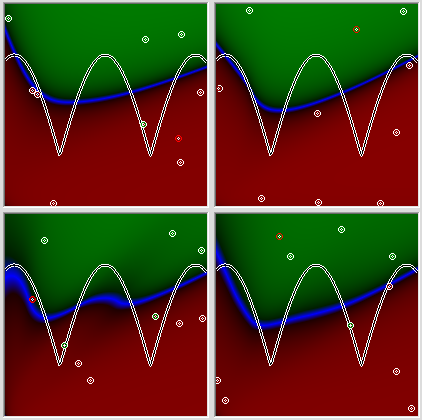
Все попытки дают, в принципе похожий, результат, и на всех картинка завалена влево, не смотря на то, что искомый график во всех этих случая расположен симметрично. Тупость сети можно списать на множество разных причин, включая ошибки в ДНК программиста, но то, что сети удобно заваливаться налево, должно иметь какое-то рациональное объяснение. Так, может быть, мы где-то ошиблись? Давайте предложим сети справиться с совсем уж банальнейшей задачей – дадим в качестве задачи простую линейную зависимость. Смотрим.
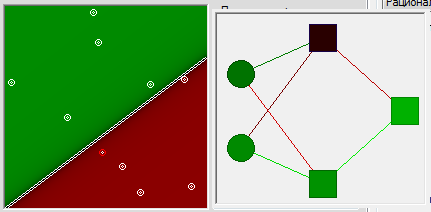
Всё хорошо, всё правильно. Отследив вручную состояние переменных можно убедиться, что алгоритм работает правильно. Тогда дадим задачку лишь немного сложнее. Результат можно видеть на следующей картинке.
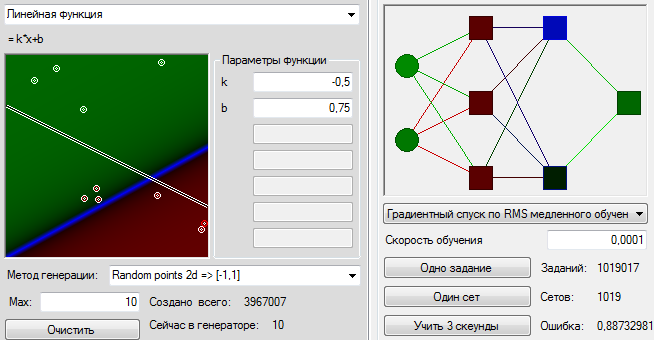
Полное Фиаско
Вот смотрим мы на это и понимаем, что что-то тут не так. Задача не то, что простая, она примитивная. Но сеть оказывается решительно не способна найти её решение ни в каком приближении.
Вы уже догадались почему? Из картинки явно следует, почему это невозможно, а заодно ответ на вопрос – почему все решения с предыдущей картинки заваливались влево.
Если мы попробуем сконструировать решение данной задачи аналитически – вручную, с ручкой и бумажкой, то очень быстро столкнёмся с правильным ответом. Если у вас в распоряжении нейрон с симметричной сигмоидой никакими ухищрениями вы не заставите его сделать преобразование output = k*input+b. Нейронная сеть с симметричной относительно нуля сигмоидой в точке (0,0) не может выдавать на выходы ничего кроме 0 (привет, кстати, теореме о сходимости перцептрона Розенблатта, там тоже есть такая особенная точка).
Чтобы решить эту проблему мы можем добавить нейронной сети ещё один вход, и выдать ему постоянное значение 1, не зависящее от входных данных. И тут сеть словно бы по мановению волшебной палочки умнеет и обучается стоящей перед ней задаче в кратчайшие сроки и с невероятной доселе точностью.
А вот тут начинается самое интересное. А может ли существовать неплохое приближение без дополнительного опорного входа? Сможем ли мы придумать решение для топологии сети с предыдущей картинки? Оказывается, это возможно.
Мозг против обратного распостранения
По ходу сети я несколько раз предлагал найти решение для сети вручную. Вот сейчас одно из таких решений мы разберём детально.
Входы сети у нас называются S[0] и S[1], нейроны первого слоя соответственно A[0][1], A[0][2] и A[0][3], следующий слой A[1][0] и A[1][1] и, наконец, выход R[0]. Чего нам не хватало в прошлый раз, когда мы пытались решать задачу аналитически? Нам не хватало опорной константы. Возьмём один нейрон, например A[0][0] и навесим его синапсам очень большие веса, например, по 1000, Кроме маленькой области в непосредственной окрестности 0, потенциал действия на данном нейроне будет равен 1.
Что дальше? A[0][1], будет у нас передавать информацию о первой координате и иметь веса синапсов соответственно 1 и 0, нейрон A[0][2] – информацию о второй координате, и иметь синапсы с весами 0 и 1. Мы хотим, чтобы функция от первой из координат сравнивалась со второй координатой. Для этого во второй нейрон второго слоя просто передадим вторую координату. Назначим веса синапсов, соответственно, 0,0 и 1. А в первом синапсе второго слоя мы хотим получить значение k*x-b. Соответственно k =-0.5 b было бы равно 0.75 если бы функции активации нейронов не погнули значения. Про входе x=1 на нейроне A[0][1] будет потенциал уже только 0,76. Значит для сравнения нам необходимо примерно b = 0.65. При таком значении на нейроне A[1][0] должно получаться примерно такое же значение, как на нейроне A[1][1] для точек, лежащих на нашей исходной прямой. Ну и теперь, чтобы сравнить два этих значения наделим выходной нейрон R[0] значениями на синапсах -1 и 1. Отобразим то, что у нас получилось на картинке. Прямо красота! Синие нулевые значения находятся примерно там, где нужно. Сверху зелёное. Снизу красное. Конечно, пока что оно недостаточно зелёное и недостаточно красное. Однако финальную доводку весов синапсов алгоритм обратного распространения ошибки сумеет сделать не только не хуже, но лучше, чем я. Запускаем алгоритм, и спустя небольшое количество шагов имеем довольно сносное приближение.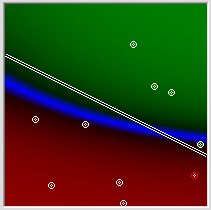
Вот можно посмотреть, как в итоге выглядит сеть:
XML-ка в которую экспортирована готовая сеть
<rumelhart>
<input>
<SensoryNeuron name="S[0]" potential="0,0396039603960396"/>
<SensoryNeuron name="S[1]" potential="0,232673267326733"/>
</input>
<excitationOrder>
<Neuron name="A[0][0]" potential="1">
<synaps weight="999,800400355468" axon="S[0]" potential="39,5960554596225" />
<synaps weight="999,545226476388" axon="S[1]" potential="232,5674536851" />
</Neuron>
<Neuron name="A[0][1]" potential="0,116342019068401">
<synaps weight="1,13712492177543" axon="S[0]" potential="0,0450346503673436" />
<synaps weight="0,308744483692756" axon="S[1]" potential="0,0718365877898986" />
</Neuron>
<Neuron name="A[0][2]" potential="0,29693700450834">
<synaps weight="-0,0240967983057654" axon="S[0]" potential="-0,000954328645772886" />
<synaps weight="1,31992553337836" axon="S[1]" potential="0,307111386479124" />
</Neuron>
<Neuron name="A[1][0]" potential="0,683083451961352">
<synaps weight="1,02404884109051" axon="A[0][0]" potential="1,02404884109051" />
<synaps weight="-0,649771926175146" axon="A[0][1]" potential="-0,0755957778251805" />
<synaps weight="-0,382508459201211" axon="A[0][2]" potential="-0,113580916074308" />
</Neuron>
<Neuron name="A[1][1]" potential="0,0324886810522597">
<synaps weight="-0,404744328902586" axon="A[0][0]" potential="-0,404744328902586" />
<synaps weight="0,161865952018599" axon="A[0][1]" potential="0,0188318116762727" />
<synaps weight="1,40909563283595" axon="A[0][2]" potential="0,418412636280091" />
</Neuron>
</excitationOrder>
<output>
<Neuron name="R[0]" potential="-0,707598983150799">
<synaps weight="-1,36308077548559" axon="A[1][0]" potential="-0,931097921420856" />
<synaps weight="1,50019153981243" axon="A[1][1]" potential="0,0487392444542643" />
</Neuron>
</output>
</rumelhart>
Во всем этом ручном решении есть один интересный момент. Дело в том, что перцептрон, ведомый алгоритмом обратного распространения ошибки, в принципе не мог найти это решение в нашей ситуации. Потому что между начальным состоянием, когда у всех синапсов начальное значение в диапазоне [-1,1] и конечным, при котором два синапса весят очень много, лежит очень широкая пропасть, наполненная очень плохими решениями, и алгоритм градиентного спуска будет старательно выталкивать сеть из этой пропасти. Как я называю это решения имеют высокую несвязанность. Алгоритм имитации отжига может случайно закинуть сеть в ту область, но для этого температура отжига должна быть большой (чтобы был шанс закинуть сеть так далеко) и очень быстро снижаться, чтобы оттуда сразу не выбросило. А ещё поскольку веса части синапсов должны быть большими, а у других, наоборот, очень мало отличаться, мы должны случайно попасть не только в большие значения, но ещё, совершенно случайно, хорошо попасть в маленькие, а ещё алгоритм должен очень резко замерзать когда что-то такое нашёл потому что область годных решений очень узенькая. Даже на скорости обучения 0.0001 простой стохастический градиентный спуск легко может выкинуть из неё сеть. В общем, есть то решение есть, да вот только найти его сеть не может.
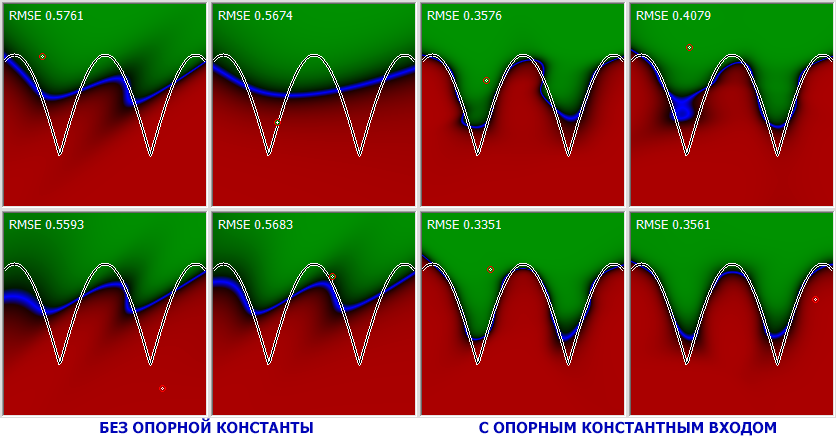
Хотя, как вы наверняка заметили, если дать в распоряжение сети три слоя по 30 нейронов, сеть может самостоятельно найти способ частично обрулить проблему нулевой точки. Хотя делать ей это сильно неудобно. Если же мы дадим сети дополнительный опорный вход, картинка перестаёт быть перекошенной на одну сторону. Но и более того сам процесс поиска решения становится гораздо более продуктивным – избавленная от необходимости тратить половину своих бесценных нейронов на создание константы сеть смогла в полную силу развернуться и повести себя так эффективно словно в ней на один слой и ещё несколько десятков нейронов больше. Подробностями можно полюбоваться на картинке.
И решение этой проблемы не единственный способ улучшать качество обучения сети в разы, манипулируя топологией. Я показал именно его просто потому что его можно было красиво продемострировать с аналитическим решением на простейшем примере.
Интересно, что добавление одного входа с константой заметно улучшает работу сети даже в случаях, когда окрестности нулевого значения не попадают во входную задачу, которой мы обучаем сеть. Например ниже я предложил обычной сети, и сети с дополнительным входом одинаковую задачу и одинаково меняющуюся скорость обучения. Причём весь график был сдвинут по обоим осям на единицу, так что на вход сети поступали значения в диапазоне от 1 до 2. Результаты говорят сами за себя.
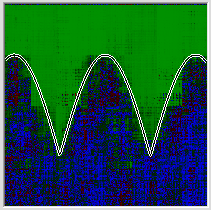
Наконец если скормить этому алгоритму первую исходную целочисленную задачу, предлагавшуюся перцептрону Розенблатта, результаты будут заметно лучше чем в прошлый раз. Но надо учитывать и то, что в многослойном перцептроне на 30 нейронов синапсов сильно больше, потому, чтобы записать данные сети требуется ощутимо больше байт, чем весят сами исходные денные.
Выводы
- Перцептрон Розенблатта можно научить только таким знаниям, которые в точке с нулевыми входами предполагают нулевой же выход. Если вы интересовались теоремой о сходимости, но не заметили что это из неё следует – значит, перечитайте её более внимательно. Ни за что не поверю, что Розенблатт или Мински могли ошибаться в доказательствах;
- Топология сети влияет на результат заметно больше, чем алгоритм обучения. Если топология делает обучение сети неудобным, скорость обучения падает в разы и даже в десятки раз, а может сделать его попросту невозможным;
- Нейронная сеть легко осваивает только те обобщения, которые легко и удобно сделать на базе её топологии. Все остальные, хоть и возможны в принципе, но или очень маловероятны, или недостижимы из начального состояния сети;
- Обобщение, которое осваивают нейронные сети, в общепринятом в наше время смысле понятие весьма условное. К нему следует относиться со здоровым скептицизмом, если не с иронией;
- То, что задача может быть в принципе решена с помощью нейронной сети, ещё совершенно не значит, что это решение может быть достигнуто из начального состояния сети. Более того связанность пространства решений должна рассматриваться как один из основных факторов при обучении нейронных сетей;
- Добавление на вход простого константного значения во очень многих случаях сильно улучшить качество работы сети для самых разных задач.
UPD: Исправил в коде ошибку. Казалось бы критическую, в реализации обратного распостранения, но почему-то все результаты работы сети не изменились. Это меня удивляет, даже больше.
