Comments 23
Хорошая статья по LINQ
Ну ладно, не только по LINQ. Автор продемонстрировал уверенные и глубокие знания всего C# и хорошее чувство вкуса при визуализации.
Что касается непосредственно ИНС то в статье рассмотрены самые азы знаний из этой области и присутствует набор неточностей, стандартный для всех, кто только начал работать с ИНС.
Не хотел никого обидеть, но статья действительно полезная с точки зрения изучения C# гораздо больше чем для ИНС.
Что касается непосредственно ИНС то в статье рассмотрены самые азы знаний из этой области и присутствует набор неточностей, стандартный для всех, кто только начал работать с ИНС.
Не хотел никого обидеть, но статья действительно полезная с точки зрения изучения C# гораздо больше чем для ИНС.
Спасибо на добром слове. :) В этом проекте я совмещал приятное с полезным. Полезная цель была выучить новый язык С#, на котором я никогда раньше не писал. Да и ИНС я раньше не занимался на уровне кода. Однако мнение о бесполезности поста, я надеюсь, несколько преувеличено.
Подробнее смотрите мой ответ zz_wolf-у в самом низу.
Подробнее смотрите мой ответ zz_wolf-у в самом низу.
Огромное спасибо за статью! Очень интересно.
Я сам в вопросах нейросетей не особо грамотен, но мне это интересно. Я как-то писал многослойный перцептрон, который решал куда более интересную задачу — распознавал взаимное расположение двух предметов на картинке. Генерировалася картинка (чёрно-белая), состоящая из жирного кольца и жирной точки. Каждый пиксель картинки подавался на вход. Перцептрои имел (если мне не изменяет память) три скрытых слоя, размеры каждого из которых были примерно в 4-6 раз меньше, чем размеры исходного изображения (входной слой, очевидно, имел размер, равный размеру исходной картинки). На выходе был один нейрон, выход которого должен был дать положительное число, если пятно внутри кольца и отрицательное, если оно вне кольца.
Обучалась эта штука, кажется, примерно часов 5 на Пентиуме 4 (написана была тоже на C#) и в итоге качество ее ответов было порядка 85%. Возможно, я что-то написал неэффективно, поэтому производительностью не хвастаюсь. Просто, к сведению…
Я сам в вопросах нейросетей не особо грамотен, но мне это интересно. Я как-то писал многослойный перцептрон, который решал куда более интересную задачу — распознавал взаимное расположение двух предметов на картинке. Генерировалася картинка (чёрно-белая), состоящая из жирного кольца и жирной точки. Каждый пиксель картинки подавался на вход. Перцептрои имел (если мне не изменяет память) три скрытых слоя, размеры каждого из которых были примерно в 4-6 раз меньше, чем размеры исходного изображения (входной слой, очевидно, имел размер, равный размеру исходной картинки). На выходе был один нейрон, выход которого должен был дать положительное число, если пятно внутри кольца и отрицательное, если оно вне кольца.
Обучалась эта штука, кажется, примерно часов 5 на Пентиуме 4 (написана была тоже на C#) и в итоге качество ее ответов было порядка 85%. Возможно, я что-то написал неэффективно, поэтому производительностью не хвастаюсь. Просто, к сведению…
Кстати, интересные результаты даёт отклик ИНН за пределами обучающей выборки. Для двухмерного вектора это наглядно поясняет некоторые ограничения при использовании ИНН и собственно, что ими можно аппроксимировать, а что не очень. Например, даёт ответ на вопрос — Способна ли ИНН аппроксимировать периодические функции.
Отклик нейросети за пределами обучающей выборки — это проверка на тестирование или валидационной выборке. Стандартная процедура должна быть при обучении ИНН.
Каким образом проверка на валидационной выборке влияет на обучение сети?
Она влияет на определение качества обучения, а не на собственно обучение.
Да, именно поэтому для двухмерного и трёхмерного вектора интересно смотреть за край обучающей выборки, для большего количества измерений можно только пытаться представить.
Просто, автор уделил много внимания именно визуализации своих результатов и расширить отклик за границы было бы поучительно. Я когда то делал так
Просто, автор уделил много внимания именно визуализации своих результатов и расширить отклик за границы было бы поучительно. Я когда то делал так
Влияет самым непосредственным образом, поскольку цель обучения сети — это по смыслу получение хорошей, работоспособной на практике модели. Поэтому после обучения сеть нужно протестировать на выборке, которая не участвовала в обучении. Если результат на тестовой выборке хуже, но не особенно сильно — ОК, эта сеть подходит. Сам по себе хороший результат на обучающей выборке ничего не говорит — сеть может переобучиться (overfitting). Популярен подход, при котором обучают много нейросетей с разными исходными весами и выбирают лучшую в смысле результатов на тесте.
Да никак работа сети (прямое распространение сигнала) на тестовой выборке не влияет на обучение конкретной сети. Результаты могут быть учтена при составлении ансамблей или принятия каких-нибудь эмпирических решений.
Повторюсь, именно поэтому, когда ответ можно получить в виде двух или трёхмерной картинки — это очень познавательно. Это наглядно демонстрирует что ИНС это аппроксимация и не более. К сожалению, не могу добавить ссылку.
Повторюсь, именно поэтому, когда ответ можно получить в виде двух или трёхмерной картинки — это очень познавательно. Это наглядно демонстрирует что ИНС это аппроксимация и не более. К сожалению, не могу добавить ссылку.
Понятие «обучение нейронной сети» можно рассматривать в узком и широком смысле. В узком смысле обучение — это сам процесс коррекции весовых коэффициентов. Когда нейронная сеть прогоняется на тестовой или валидационной выборках — коррекция весов, естественно, не происходит. В широком смысле обучение нейросети — это получение валидной модели на эмпирических данных, оно включает в себя разные этапы. Этап тестирования должен обязательно присутствовать во время такого процесса, это стандартные методы Machine Learning, тут просто нечего обсуждать.
Но не имею ничего против визуализации процессов обучения. К сожалению, это редко бывает возможно на реальных задачах с большими данными.
Но не имею ничего против визуализации процессов обучения. К сожалению, это редко бывает возможно на реальных задачах с большими данными.
Вопросы, описанные в настоящей статье давным-давно изучены и описаны во множестве статей и учебников. Можно похвалить автора за аккуратность, прилежание и упорство в моделировании нейросетей, это вызывает искреннюю симпатию к автору. Но есть ряд замечаний по существу. Главный смысл — сообщение находится на уровне понимания нейронауки в конце 1980-х — начала 1990-х годов, такое впечатление, что опыты делались по некой старой книжке типа Уоссермена.
1. Существенное различие между персептроном Розенблатта и многослойным персептроном — это линейность первого и нелинейность второго. Это очень важно. Синус — это нелинейная функция, поэтому первая модель не может ее моделировать хорошо в принципе. Персептрон Розентблатта сейчас — это такая историческая модель, не имеющая реального практического применения, используется крайне редко. «Многослойный персептрон Румельхарта» — так давно не говорят. Просто многослойный персептрон, MLP.
2. Топология нейросети влияет сильно, только если вы используете устаревшие простые алгоритмы вроде чистого backpropagation. Если используются более новые методы второго порядка — сопряженные градиенты, Левенберг-Марквардт, BFGS — там почти все равно на топологию. Оно жмет очень сильно. Но нужно использовать регуляризацию, иначе будет переобучение (overfitting).
3. Обобщение (generalization) — понятие вполне определенное в машинном обучение. Следует относиться к нему как к математическому понятию.
4. «Опорная константа», как я понял, параметр b, если слой рассчитывается как z = tanh(Ax + b) — да, нужна, выборка не центрирована около 0. Что об этом много говорить.
Хочу посоветовать автору новые хорошие книжки по машинному обучению и нейронным сетям — «С. Осовский. Нейронные сети для обработки информации» и «Bishop C.M. Pattern Recognition and Machine Learning». Думаю, что проработав их с таким же упорством, которое было при подготовке данной статьи, автор добьется отличных результатов.
Желаю успехов!
1. Существенное различие между персептроном Розенблатта и многослойным персептроном — это линейность первого и нелинейность второго. Это очень важно. Синус — это нелинейная функция, поэтому первая модель не может ее моделировать хорошо в принципе. Персептрон Розентблатта сейчас — это такая историческая модель, не имеющая реального практического применения, используется крайне редко. «Многослойный персептрон Румельхарта» — так давно не говорят. Просто многослойный персептрон, MLP.
2. Топология нейросети влияет сильно, только если вы используете устаревшие простые алгоритмы вроде чистого backpropagation. Если используются более новые методы второго порядка — сопряженные градиенты, Левенберг-Марквардт, BFGS — там почти все равно на топологию. Оно жмет очень сильно. Но нужно использовать регуляризацию, иначе будет переобучение (overfitting).
3. Обобщение (generalization) — понятие вполне определенное в машинном обучение. Следует относиться к нему как к математическому понятию.
4. «Опорная константа», как я понял, параметр b, если слой рассчитывается как z = tanh(Ax + b) — да, нужна, выборка не центрирована около 0. Что об этом много говорить.
Хочу посоветовать автору новые хорошие книжки по машинному обучению и нейронным сетям — «С. Осовский. Нейронные сети для обработки информации» и «Bishop C.M. Pattern Recognition and Machine Learning». Думаю, что проработав их с таким же упорством, которое было при подготовке данной статьи, автор добьется отличных результатов.
Желаю успехов!
Огромное спасибо за ссылки,
Полезно будет знакомиться не со всем подряд, а с тем, что нужно. Отдельное спасибо за упоминание сопряжённых градиентов. А то я тут уже переоткрыл подобный метод и как раз начинал его писать.
Однако в том, что касается идеи опорного входа вы не совсем правы. Добавление входа не идентично добавлению константы в функцию активации. Мало того, что это сильно проще, важнее, что это сильно улучшает качество сети. Если просто добавить константу в функцию активации, то придётся ещё как минимум один слой в сеть добавить, чтобы достичь похожих результатов.
И центрирование выборки тоже всего лишь слабое подобие. Я для иллюстрации взял задачу, которая строго отцентрована. Значения сдвинуты на 0.5 так чтобы точка (0,0) оказывалась строго в центре экрана, кроме того значение функции в центре экрана, в точке (0,0) равно 0, а площадь над кривой и под кривой одинаковы. Таким образом вероятность появления обучающих примеров на +1 и -1 одинаковы. В общем отцентровал всё идеально. Получилась вот такая задачка и её решение сетью с дополнительным входом:
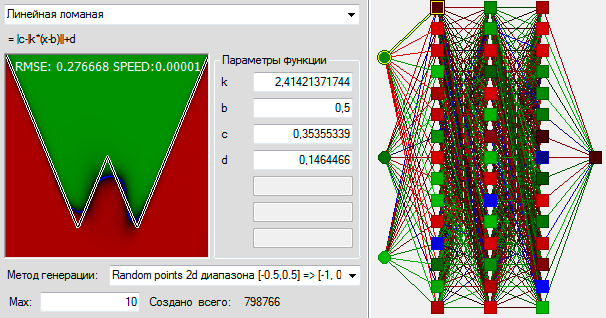
Вот так выглядит решение задачи сетью с дополнительным входом, когда площади над и под кривой равны, но координаты не сдвинуты, область входных значений (0,1):

А теперь отключим дополнительный вход, и посмотрим как себя поведёт обычная сеть. На нецентрованных данных предсказуемо картинка заваливается в направлении особой точки, тоесть влево:

А вот если данные отцентровать получается самое интересное:

Сеть попадает в тупик и не может решить задачу. Специально 5 раз прогнал.
Возможно обратное распространение это самый старый и примитивный алгоритм из тех, что существуют в ИНС, но моё простое и почти незаметное изменение позволяет ему решить нецентрированные задачи лучше, чем сеть без этого дополнения справляется с любыми, хоть центрированными, хоть нет.
Я стал на много лучше понимать, что и почему творится внутри сетей благодаря этому примеру. Возможно и вы сможете вынести что-то для себя, в том числе и для более сложных сетей и алгоритмов, если рассмотрите эту идею чуть более обстоятельно.
Если вдруг у вас под рукой есть сеть с более качественным алгоритмом обучения вы сможете сравнить его успехи с моими. Результат может быть парадоксальным образом не такой уж хороший. Если сделаете это — поделитесь со мной картинкой, буду благодарен.
Область входных значений для графика (0,1)
График: = |c-|k*(x-b)||+d
Константы, при которых задаяча отцентрирована:
Значения сдвигаются на 0,5 чтобы входные данные тоже были центрированы:
Сеть, как и в прошлый раз, три слоя по 15 нейронов.
То что в работе есть хорошо узнаваемые вами проблемы, к счастью, не значит, что в ней нетчего-то, что было бы новым даже для вас.
Полезно будет знакомиться не со всем подряд, а с тем, что нужно. Отдельное спасибо за упоминание сопряжённых градиентов. А то я тут уже переоткрыл подобный метод и как раз начинал его писать.
Однако в том, что касается идеи опорного входа вы не совсем правы. Добавление входа не идентично добавлению константы в функцию активации. Мало того, что это сильно проще, важнее, что это сильно улучшает качество сети. Если просто добавить константу в функцию активации, то придётся ещё как минимум один слой в сеть добавить, чтобы достичь похожих результатов.
И центрирование выборки тоже всего лишь слабое подобие. Я для иллюстрации взял задачу, которая строго отцентрована. Значения сдвинуты на 0.5 так чтобы точка (0,0) оказывалась строго в центре экрана, кроме того значение функции в центре экрана, в точке (0,0) равно 0, а площадь над кривой и под кривой одинаковы. Таким образом вероятность появления обучающих примеров на +1 и -1 одинаковы. В общем отцентровал всё идеально. Получилась вот такая задачка и её решение сетью с дополнительным входом:

Вот так выглядит решение задачи сетью с дополнительным входом, когда площади над и под кривой равны, но координаты не сдвинуты, область входных значений (0,1):

А теперь отключим дополнительный вход, и посмотрим как себя поведёт обычная сеть. На нецентрованных данных предсказуемо картинка заваливается в направлении особой точки, тоесть влево:

А вот если данные отцентровать получается самое интересное:

Сеть попадает в тупик и не может решить задачу. Специально 5 раз прогнал.
Возможно обратное распространение это самый старый и примитивный алгоритм из тех, что существуют в ИНС, но моё простое и почти незаметное изменение позволяет ему решить нецентрированные задачи лучше, чем сеть без этого дополнения справляется с любыми, хоть центрированными, хоть нет.
Я стал на много лучше понимать, что и почему творится внутри сетей благодаря этому примеру. Возможно и вы сможете вынести что-то для себя, в том числе и для более сложных сетей и алгоритмов, если рассмотрите эту идею чуть более обстоятельно.
Если вдруг у вас под рукой есть сеть с более качественным алгоритмом обучения вы сможете сравнить его успехи с моими. Результат может быть парадоксальным образом не такой уж хороший. Если сделаете это — поделитесь со мной картинкой, буду благодарен.
Область входных значений для графика (0,1)
График: = |c-|k*(x-b)||+d
func = (point, envirement) => Math.Abs(envirement[2]-Math.Abs(envirement[0]*(point[0]-envirement[1])))+envirement[3]Константы, при которых задаяча отцентрирована:
envirement[1] = 0.5envirement[2] = SQRT(1/8) = 0.35355339envirement[3] = 1/(4+2*SQRT(2)) = 0.1464466envirement[0] = SQRT(1/8)/envirement[3] = 2.41421371744Значения сдвигаются на 0,5 чтобы входные данные тоже были центрированы:
Convertion = (double[] input, double value) => {
NeuralTask result = new NeuralTask() {
input = new double[]{input[0]-0.5, input[1]-0.5},
output = new double[1] { Math.Sign(input[1] - value) }
};
result.preview = new double[3] { input[0], input[1], result.output[0]};
return result;
}
Сеть, как и в прошлый раз, три слоя по 15 нейронов.
То что в работе есть хорошо узнаваемые вами проблемы, к счастью, не значит, что в ней нетчего-то, что было бы новым даже для вас.
Не ту картинку подцепил на сеть с дополнительным входом без центрирования координат:
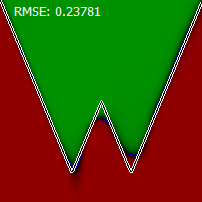

Исходники нельзя выложить? Обособленные куски кода не очень удобно изучать.
К сожалению в полных исходниках куски моих других экспериментов, которые ещё не готовы к публикации. Очень хотелось бы не раздавать их раньше времени.
Сегодня в реализации обратного распостранения нашёл критическую ошибку. Удивительнее всего для меня, что и неправильно написанное обратное распостранение успешно работало, давая точно такой же результат. Если уже воспользовались кодом перезалейте этот кусок ещё раз.
А какого сорта ошибка?
Должно быть:
Было:
Тоесть умножение происходило не на производную в целевом нейроне, а на производную в текущем. Знак изменения передавался правильно, а вот величина немного нет.
Грубо говоря, если мы возьмём произвольную dE^2/wij lk любого например синапса, то она должна в общем случае быть равна примерно следующему, для синапса нерона второго с конца слоя:
dE^2/Wij = 2(OUT[k] — REQUIRED[k])*F'[k]*W[l,k]*F'[l]*W[j,l]*F'[j]*A[i]
А вместо этого получилось:
dE^2/Wij := 2(OUT[k] — REQUIRED[k])*F'[k]*W[[l,k]*F'[k]*W[j,l]*F'[l]*A[i]
Судя по тому, что результаты отличаются очень не сильно, такая функция хоть и не является непосредствено производной, но, по всей видимости, остаётся достаточно хорошей эвристической функцией.
(synaps.Axon as NeuronWithDerivative).BackProprigationParametr += neuron.BackProprigationParametr * (synaps.Axon as NeuronWithDerivative).ActionPotentialDerivative * synaps.Weight;Было:
(synaps.Axon as NeuronWithDerivative).BackProprigationParametr += neuron.BackProprigationParametr * neuron.ActionPotentialDerivative * synaps.Weight;Тоесть умножение происходило не на производную в целевом нейроне, а на производную в текущем. Знак изменения передавался правильно, а вот величина немного нет.
Грубо говоря, если мы возьмём произвольную dE^2/wij lk любого например синапса, то она должна в общем случае быть равна примерно следующему, для синапса нерона второго с конца слоя:
dE^2/Wij = 2(OUT[k] — REQUIRED[k])*F'[k]*W[l,k]*F'[l]*W[j,l]*F'[j]*A[i]
А вместо этого получилось:
dE^2/Wij := 2(OUT[k] — REQUIRED[k])*F'[k]*W[[l,k]*F'[k]*W[j,l]*F'[l]*A[i]
Судя по тому, что результаты отличаются очень не сильно, такая функция хоть и не является непосредствено производной, но, по всей видимости, остаётся достаточно хорошей эвристической функцией.
Написал свою третюю статью про нейронные сети:
habrahabr.ru/post/249031/
habrahabr.ru/post/249031/
Не совсем понятно зачем так реализовывать нейросеть??
Смотрите, у Вас есть матрица весов W, вектор-функция активации F(n), вектор входа X, вектор смещения B, тогда прохождение одного слоя записывается как Y = F(WX+B)
Если у вас плотная сеть в которой все связаны со всеми предыдущего слоя, тогда да. А если у вас 36 нейронов распологаются в примерно 20 слоях, как в моей следующей статье, и каждый может быть связан с нейроном из любого предыдущего слоя, тогда просто матрицы уже плохо подходят. Ну то есть на самом деле и такое можно выразить через матрицы, и я это уже сделал. Но в первом приближении было удобнее реализовывать таким вот медленным и убогим способом.
Sign up to leave a comment.
Что происходит в мозгах у нейронной сети и как им помочь