
В этом посте я хочу рассказать о своём опыте расчётов на суперкомпьютере Ломоносов. Я расскажу о решении задачи, честно говоря, для которой не нужно использовать СК, но академический интерес превыше всего. Подробную информацию о конфигурации Ломоносова можно найти тут.
Скорость передачи данных между узлами/процессами
Сначала я решил провести простой тест пропускной способности кластера, и сравнить на сколько отличаются скорости передачи данных от одного потока другому а) если оба потока запущены на одном узле кластера; б) на разных. Следующие значения оценены с помощью теста mpitests-osu_bw.
Пиковая скорость на разных узлах:
3,02 ГБайт/с.
На одном узле:
10,3 ГБайт/с
Немного о задаче
Нужно решить уравнение диффузии на довольно простой области.
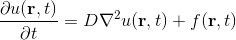
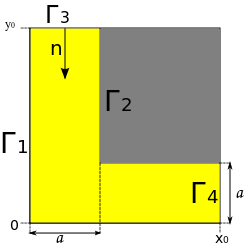
Мы имеем линейное уравнение в ч.п. Будем его решать без потока, т.е. на границах 1, 2, 4 производная по нормали к стенке 0, а на границе 3 концентрация определяется заданной функцией g(t). Таким образом мы получаем смешанную краевую задачу. Будем решать её методом конечных разностей (очень не эффективно, зато просто).
О распараллеливании
Для решения этой задачи я пользовался openMPI/intelMPI (отдельный пост стоит посвятить сравнению компиляторов на практике). Я не буду углубятся в численную схему, ибо есть википедия и скажу только, что использовал явную схему. Я использовал блочное распределение области так, что каждому потоку даётся несколько областей и если, данные которые передаются из предыдущей области ноль, то область не считается. Крайние столбцы/строки блоков предназначены для получения данных от соседних потоков.
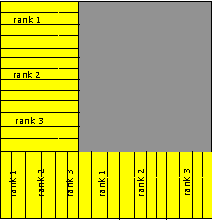
Параметры сетки используемые при вычислениях
Количество узлов в сетке: 3*10^6
Шаг по сетке: 0.0007.
Физическое время диффузии: 1 с
Шаг по времени: 6,5*10^-7
D: 0.8
Начальная концентрация на границе 3 0,01 моль.
Немного о законе Амдала
Джим Амдал сформулировал закон, иллюстрирующий ограничение производительности вычислительной системы с увеличением числа вычислителей. Предположим, что необходимо решить какую-либо вычеслительную задачу. Пусть α- доля алгоритма которая выполняется последовательно. Тогда, соответственно, 1-α выполняется параллельно и может быть распараллелена на p-узлах, тогда ускорение полученное на вычислительной системы можно получить как

Перейдём к самому интересному к результатам и результатам распараллеливания
Времена выполнения на различном количестве потоков
| кол-во проц. | 1 | 2 | 8 | 16 | 32 | 64 | 128 |
| время, мин. | 840 | 480 | 216 | 112 | 61 | 46 | 41 |
Аппроксимируем времена вычисления законом Амдала.
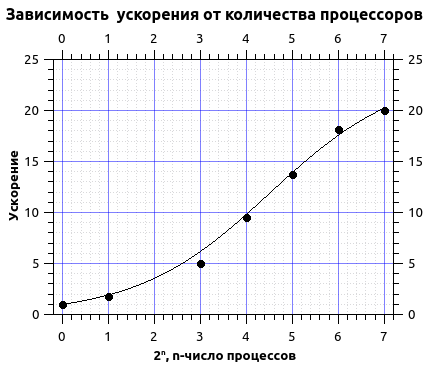
Из аппроксимации я получил долю последовательного кода порядка 4,2% и максимальное ускорение порядка 20 раз. Как видно из графика кривая выходит на плато, из этого можно сделать вывод, что достигается максимум ускорения и дальнейшее увлечение числа процессоров нецелесообразно. Более того в данном случае при увеличении числа процессов более 200 я получил спад ускорения, это связано с тем, что при увеличении числа процессов начинается нерациональное их использование, т.е. количеств строк в сетке становится соизмеримым с числом процессов и затрачивается больше времени на обмены и это время вносит заметный вклад во время вычислений.
Некоторые замечания
На СК используется система управления задачами sbatch и имеется несколько очередей test, regular4, regular6, gputest, gpu. Для данной задачи я использовал очередь regular4 время ожидания в которой может достигать трёх суток (на практике же время ожидания 17-20 часов).
