saluev 27 янв 2015 в 02:16

C++11 variadic templates и длинная арифметика на этапе компиляции

23 мин

20K

C++*Ненормальное программирование*Программирование*

Туториал

За тридцать лет, прошедших с момента его появления в недрах Bell Labs, C++ проделал долгий путь, пройдя от «усовершенствованного C» до одного из самых популярных и выразительных компилируемых языков. Особенно много, на авторский сугубо личный взгляд, дал C++ новый стандарт C++11, стремительно обретающий поддержку компиляторов. В этой статье мы постараемся «пощупать руками» одну из его мощнейших фич — шаблоны с переменным числом аргументов (variadic templates).

Разработчики, знакомые с книжками Александреску, вероятно, помнят концепцию списка типов. В старом-добром C++03 при необходимости использовать заранее неизвестное число аргументов шаблона предлагалось создать такой список и потом хитрым хаком его использовать. Этим способом реализовывались кортежи (ныне std::tuple) и проч. и проч. А сама глава про списки типов ясно давала понять, что на шаблонах C++ можно проводить практически любые вычисления (заниматься λ-исчислением, например), лишь бы их можно было записать в функциональном стиле. Эту же концепцию можно было бы применить и к длинной арифметике: хранить длинные числа как списки intов, вводить основной класс вида

template<int digit, class Tail> struct BigInteger { };

, операции над ним и так далее. Но во славу нового стандарта мы пойдём другим путём.

Parameter packs

Итак, основа основ — это новый синтаксис, введённый в C++11. Для начала рассмотрим, как же должно выглядеть определение класса tuple, не являющееся преступлением против человечества:

template<typename... Types>
class tuple {
    // ...
};

Обратите внимание на троеточие в аргументах шаблона. Теперь Types — не имя типа, а parameter pack — совокупность нуля или более произвольных типов. Как его использовать? Хитро.

Первый способ: как набор типов аргументов функций или методов. Это делается так:

template<typename... Types>
void just_do_nothing_for_no_reason(Types... args) {
    // indeed
}

Здесь Types... args — другая специальная синтаксическая конструкция (function parameter pack), которая разворачивается в соответствующую parameter pack'у цепочку аргументов функции. Поскольку C++ поддерживает автоопределение аргументов шаблонных функций, эту нашу функцию теперь можно вызывать с любым количеством аргументов любого типа.

Ну а дальше-то что? Что с этими всеми аргументами можно делать?

Во-первых, можно просто использовать дальше, как типы других функций или шаблонов с переменным числом аргументов:

template<typename... Types>
tuple<Types...> make_tuple(Types... args) {
    tuple<Types...> result(args...);
    return result;
}

Types... args мы уже знаем. args... — ещё одна специальная конструкция (parameter pack expansion), которая в данном случае развернётся в список аргументов функции, разделённых запятой. Так, если поставить где-нибудь в коде вызов make_tuple(1, 1.f, '1'), то будет создана и вызвана функция вида

tuple<int, float, char> make_tuple(int a1, float a2, char a3) {
    tuple<int, float, char> result(a1, a2, a3);
    return result;
}

Во-вторых, можно использовать в более сложных преобразованиях. На самом деле parameter pack expansion поддерживает больше, чем просто подстановку всего и вся через запятую. Так, можно запросто реализовать следующую функцию:

template<typename... Types>
std::tuple<Types...> just_double_everything(Types... args) {
    std::tuple<Types...> result((args * 2)...); // OMG
    return result;
}

Ииии — да, вы угадали! Конструкция ((args * 2)...) развернётся в (a1 * 2, a2 * 2, a3 * 2).

Ну и, наконец, в-третьих (и в самых банальных), списки аргументов можно использовать в рекурсии:

template<typename T>
std::ostream& print(std::ostream& where, const T& what) {
    return where << what;
}

template<typename T, typename... Types>
std::ostream& print(std::ostream& where, const T& what, const Types& ... other) {
    return print(where << what << ' ', other...);
}

На выходе получаем типобезопасный printf — определённо стоило того!

С помощью определённого количества шаблонной магии можно научиться извлекать из pack'ов тип и значение по номеру и производить прочие махинации. Пример под спойлером.

Распечатка кортежей

template<int ...>
struct seq { };   // просто статический список чисел

template<int N, int... S> // генератор списка по типу Python'овского range()
struct make_range : make_range<N-1, N-1, S...> { };

template<int ...S>
struct make_range<0, S...> {
  typedef seq<S...> result;
};

template<typename... Types, int... range>
std::ostream& operator_shl_impl(
        std::ostream& out,
        const std::tuple<Types...>& what,
        const seq<range...> /* a dummy argument */ ) {
    return print(out, std::get<range>(what)...);
}

template<typename... Types>
std::ostream& operator<<(std::ostream& out, const std::tuple<Types...>& what) {
    using range = typename make_range<sizeof...(Types)>::result;
    return operator_shl_impl(out, what, range());
}

Здесь мы видим ещё не упомянутую, но довольно простую для понимания команду sizeof...(Types) — она возвращает количество типов в parameter pack'е. Кстати, её можно реализовать самостоятельно.

Итак, вся суть в строчке

print(out, std::get<range>(what)...);

Она делает не что иное, как вызывает функцию с аргументами из кортежа. Вы только подумайте! Именно для этого фокуса нам и потребовался список чисел от 0 до (n − 1) — именно благодаря ему эта строчка разворачивается в нечто вроде

print(out, std::get<0>(what), std::get<1>(what), std::get<2>(what));

Напишите генератор списка от (n − 1) до 0 — и вы сможете разворачивать кортежи одной строчкой:

auto reversed_tuple = std::make_tuple(std::get<rev_range>(my_tuple)...);

Мораль: pack expansion — убойный инструмент.

Длинная арифметика

Начнём нашу реализацию длинной арифметики. Для начала определим основной класс:

template<uint32_t... digits>
struct BigUnsigned {
    static const size_t length = sizeof...(digits); // количество аргументов
};
using Zero = BigUnsigned< >;
using One  = BigUnsigned<1>;

В лучших традициях вычислений на этапе компиляции в C++ все, собственно, данные здесь не хранятся где-либо, а являются непосредственными аргументами шаблона. C++ будет различать реализации класса BigUnsigned с разными наборами параметров, за счёт чего мы сможем реализовать наши вычисления. Условимся, что первый параметр будет содержать младшие 32 бита нашего длинного числа, а последний — самые старшие 32, включая, возможно, ведущие нули (лично мне это видится самым логичным решением).

Прежде, чем заняться реализацией сложения, давайте определим на наших длинных числах операцию конкатенации. На примере этой операции мы познакомимся со стандартной тактикой, которую будем использовать в дальнейшем.

Итак, определим операцию над двумя типами:

template<class A, class B>
struct Concatenate {
    using Result = void;
};

Мы подразумеваем, что этими двумя типами будут реализации BigUnsigned. Реализуем операцию для них:

template<uint32_t... a, uint32_t... b>
struct Concatenate<BigUnsigned<a...>, BigUnsigned<b...>> { // >> - не проблема для C++11
    using Result = BigUnsigned<a..., b...>; // да! просто перечислим их подряд!
};

Не менее тривиально можно реализовать битовые операции, например, (очень наивный) xor:

template<class A, class B> struct Xor;
template<uint32_t... a, uint32_t... b>
struct Xor<BigUnsigned<a...>, BigUnsigned<b...>> {
    using Result = BigUnsigned< (a^b)... >; // будет работать, но только когда длина a и b совпадает
};

Теперь, собственно, сложение. Никуда не деться — придётся воспользоваться рекурсией. Определим основной класс и базу рекурсии:

template<class A, class B> struct Sum;
template<class A> struct Sum<Zero,    A> { using Result = A;    };
template<class A> struct Sum<   A, Zero> { using Result = A;    };
// если не определить этот частный случай отдельно, компилятор будет колебаться между предыдущими двумя:
template<       > struct Sum<Zero, Zero> { using Result = Zero; };

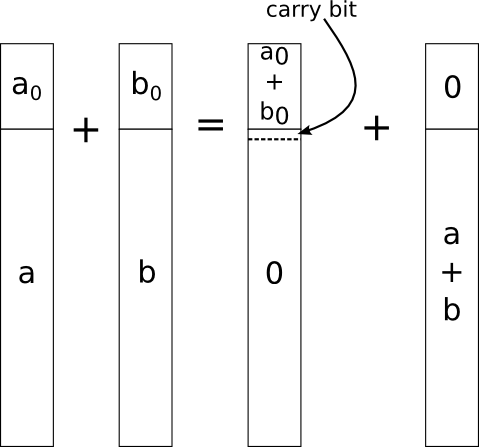
Теперь — основные вычисления:

template<uint32_t a_0, uint32_t... a_tail, uint32_t b_0, uint32_t... b_tail>
struct Sum<BigUnsigned<a_0, a_tail...>, BigUnsigned<b_0, b_tail...>> {
    static const uint32_t carry = b_0 > UINT32_MAX - a_0 ? 1 : 0;
    using Result = typename Concatenate<
        BigUnsigned<a_0 + b_0>,
        typename Sum<
            typename Sum<
                BigUnsigned<a_tail...>, BigUnsigned<b_tail...>
            >::Result,
            BigUnsigned<carry>
        >::Result
    >::Result;
};

Итак, что же произошло.

Шаблон вида

template<uint32_t a_0, uint32_t... a_tail, uint32_t b_0, uint32_t... b_tail>
struct Sum<BigUnsigned<a_0, a_tail...>, BigUnsigned<b_0, b_tail...>> {

нужен нам, чтобы отделить самые младшие разряды длинных чисел от всех старших. Если бы мы использовали шаблон более общего вида

template<uint32_t a..., uint32_t b...>
struct Sum<BigUnsigned<a...>, BigUnsigned<b...>> {

, то это сделать было бы не так-то просто и нам потребовалось бы ещё несколько вспомогательных структур. (Зато можно было бы написать их с умом и впоследствии реализовать умножение Карацубы, ня!)

Далее, строка

    static const uint32_t carry = b_0 > UINT32_MAX - a_0 ? 1 : 0;

вычисляет так называемый carry bit, указывающий, произошло ли переполнение в текущем разряде или нет. (Вместо константы UINT32_MAX можно и стоит использовать std::numeric_limits.)

Наконец, финальное вычисление находит результат, применяя рекурсию по правилу

Что ж, можно тестировать! Непосредственно вычисления будут выглядеть примерно так:

using A = BigUnsigned<0xFFFFFFFFFFFFFFFFULL>;
using B = One;
using C = Sum<A, B>::Result;
int main(int argc, char** argv) {
    // ...
}

Скомпилировалось! Запустилось! Но… как узнать значение C? Как, собственно, тестировать-то?

Простой способ: давайте вызовем ошибку на этапе компиляции. Например, напишем в main

int main(int argc, char** argv) {
    C::entertain_me();
}

При попытке скомпилировать такой код получим закономерную ошибку:

static_bignum.cpp: В функции «int main(int, char**)»:
static_bignum.cpp:32:5: ошибка: «entertain_me» не является элементом «C {aka static_bignum::BigUnsigned<0, 1>}»
     C::entertain_me();
     ^

Однако, этим нытьём об ошибке g++ выдал нам главный секрет — теперь мы видим, что C равно static_bignum::BigUnsigned<0, 1>, то есть 2³² — всё сошлось!

Менее простой способ: давайте напишем функцию, которая будет генерировать строку с бинарным представлением заданного числа. Заготовка будет выглядеть примерно так:

template<class A> struct BinaryRepresentation;
template<uint32_t a_0, uint32_t... a>
struct BinaryRepresentation<BigUnsigned<a_0, a...>> {
    static std::string str(void) {
        // ...
    }
};

Воспользуемся стандартным объектом std::bitset, чтобы распечатывать текущие 32 бита на каждом этапе:

template<class A> struct BinaryRepresentation;
template<uint32_t a_0, uint32_t... a>
struct BinaryRepresentation<BigUnsigned<a_0, a...>> {
    static std::string str(void) {
        std::bitset<32> bset(a_0);
        return BinaryRepresentation<BigUnsigned<a...>>::str() + bset.to_string();
    }
};

Осталось только задать базу рекурсии:

template<>
struct BinaryRepresentation<Zero> {
    static std::string str(void) {
        return "0b"; // Oppa Python Style
    }
};

Новая версия нашего примитивного теста будет выглядеть как

using A = BigUnsigned<0xFFFFFFFFFFFFFFFFULL>;
using B = One;
using C = Sum<A, B>::Result;
int main(int argc, char** argv) {
    std::cout << BinaryRepresentation<C>::str() << std::endl;
}

и выдаст нам просто потрясающий своей читабельностью ответ

0b00000000000000000000000000000000000000000000000000000000000000010000000000000000000000000000000000000000000000000000000000000000

Впрочем, внимательным подсчётом количества нулей можно убедиться, что это всё ещё 2³²!

Сложный, но наиболее убедительный способ — вывод десятичного представления — потребует от нас определённого труда, а именно реализации операции деления.

Для этого нам потребуются определённые, эмм, prerequisites.

Реализация вычитания

template<class A, class B>
struct Difference;

struct OverflowError {}; // класс-индикатор ошибки (вычли большее число из меньшего)

// вычитание нуля из нуля -- ну эт мы умеем:
template<> struct Difference<Zero, Zero> { using Result = Zero; };

template<uint32_t n, uint32_t... tail> // вычитание нуля -- довольно просто
struct Difference<BigUnsigned<n, tail...>, Zero> { using Result = BigUnsigned<n, tail...>; };

template<uint32_t n, uint32_t... tail> // вычитание из нуля -- довольно однозначно
struct Difference<Zero, BigUnsigned<n, tail...>> { using Result = OverflowError; };

template<class A> struct Difference<OverflowError, A> { using Result = OverflowError; };
template<class A> struct Difference<A, OverflowError> { using Result = OverflowError; };

template<uint32_t a_n, uint32_t b_n, uint32_t... a_tail, uint32_t... b_tail>
struct Difference<BigUnsigned<a_n, a_tail...>, BigUnsigned<b_n, b_tail...> > {
    using A = BigUnsigned<a_n, a_tail...>; // вводим короткие имена для удобства
    using B = BigUnsigned<b_n, b_tail...>;
    using C = typename Difference<BigUnsigned<a_tail...>, BigUnsigned<b_tail...>>::Result;
    using Result_T = typename std::conditional< // есть перенос или нет?
        a_n >= b_n, C, typename Difference<C, One>::Result
    >::type;
    using Result = typename std::conditional< // убираем возможные ведущие нули
        a_n == b_n && std::is_same<Result_T, Zero>::value,
        Zero,
        typename Concatenate<
            BigUnsigned<a_n - b_n>,
            Result_T
        >::Result
    >::type;
};

Реализация битовых сдвигов

Определим основные классы и зададим базу рекурсии:

template<class A, size_t shift> struct ShiftLeft;
template<class A, size_t shift> struct ShiftRight;
template<class A, size_t shift> struct BigShiftLeft;
template<class A, size_t shift> struct BigShiftRight;
template<class A, size_t shift> struct SmallShiftLeft;
template<class A, size_t shift> struct SmallShiftRight;

template<size_t shift> struct BigShiftLeft   <Zero, shift> { using Result = Zero; };
template<size_t shift> struct BigShiftRight  <Zero, shift> { using Result = Zero; };
template<size_t shift> struct SmallShiftLeft <Zero, shift> { using Result = Zero; };
template<size_t shift> struct SmallShiftRight<Zero, shift> { using Result = Zero;
    static const uint32_t carry = 0;
};
template<uint32_t... a> struct BigShiftLeft   <BigUnsigned<a...>, 0> { using Result = BigUnsigned<a...>; };
template<uint32_t... a> struct BigShiftRight  <BigUnsigned<a...>, 0> { using Result = BigUnsigned<a...>; };
template<uint32_t... a> struct SmallShiftLeft <BigUnsigned<a...>, 0> { using Result = BigUnsigned<a...>; };
template<uint32_t... a> struct SmallShiftRight<BigUnsigned<a...>, 0> { using Result = BigUnsigned<a...>;
    static const uint32_t carry = 0;
};

Я решил, что логично разделить любой битовый сдвиг на поочерёдное применение малого (сдвиг меньше 32 бит) и большого (сдвиг кратен 32 битам), поскольку их реализации существенно отличаются. Итак, большой сдвиг:

template<uint32_t... a, size_t shift>
struct BigShiftLeft<BigUnsigned<a...>, shift> {
    using Result = typename Concatenate<
        BigUnsigned<0>,
        typename BigShiftLeft<
            BigUnsigned<a...>,
            shift - 1
        >::Result
    >::Result;
};

template<uint32_t a_0, uint32_t... a_tail, size_t shift>
struct BigShiftRight<BigUnsigned<a_0, a_tail...>, shift> {
    using Result = typename BigShiftRight<
        BigUnsigned<a_tail...>,
        shift - 1
    >::Result;
};

Здесь shift обозначает сдвиг на 32 ⋅ shift бит, и сама операция просто «съедает» или добавляет поочерёдно целые 32-битные слова.

Малый сдвиг — это уже чуть более тонкая работа:

template<uint32_t a_0, uint32_t... a_tail, size_t shift>
struct SmallShiftLeft<BigUnsigned<a_0, a_tail...>, shift> {
    static_assert(shift < 32, "shift in SmallShiftLeft must be less than 32 bits");
    static const uint32_t carry = a_0 >> (32 - shift);
    using Result = typename Concatenate<
        BigUnsigned<(a_0 << shift)>,
        typename Sum< // Хватило бы Or или Xor, но Sum у нас уже есть
            typename SmallShiftLeft<BigUnsigned<a_tail...>, shift>::Result,
            BigUnsigned<carry>
        >::Result
    >::Result;
};

template<uint32_t a_0, uint32_t... a_tail, size_t shift>
struct SmallShiftRight<BigUnsigned<a_0, a_tail...>, shift> {
    static_assert(shift < 32, "shift in SmallShiftRight must be less than 32 bits");
    static const uint32_t carry = a_0 << (32 - shift);
    using Result = typename Concatenate<
        BigUnsigned<(a_0 >> shift) | SmallShiftRight<BigUnsigned<a_tail...>, shift>::carry>,
        typename SmallShiftRight<BigUnsigned<a_tail...>, shift>::Result
    >::Result;
};

Здесь снова приходится заботиться об аккуратном переносе бит.

Наконец, просто сдвиг:

template<class A, size_t shift>
struct ShiftLeft {
    using Result = typename BigShiftLeft<
        typename SmallShiftLeft<A, shift % 32>::Result,
        shift / 32
    >::Result;
};

template<class A, size_t shift>
struct ShiftRight {
    using Result = typename SmallShiftRight<
        typename BigShiftRight<A, shift / 32>::Result,
        shift % 32
    >::Result;
};

Как и обещано, он просто грамотно использует большой и маленький сдвиги.

Реализация операций сравнения

template<class A, class B> struct GreaterThan;
template<class A, class B> struct GreaterThanOrEqualTo;

template<class A> struct GreaterThan<Zero, A>             { static const bool value = false; };
template<class A> struct GreaterThanOrEqualTo<Zero, A>    { static const bool value = false; };
template<       > struct GreaterThanOrEqualTo<Zero, Zero> { static const bool value = true;  };

template<uint32_t n, uint32_t... tail>
struct GreaterThanOrEqualTo<BigUnsigned<n, tail...>, Zero> {
    static const bool value = true;
};

template<uint32_t n, uint32_t... tail>
struct GreaterThan<BigUnsigned<n, tail...>, Zero> {
    static const bool value = n > 0 || GreaterThan<BigUnsigned<tail...>, Zero>::value;
};

template<uint32_t a_n, uint32_t b_n, uint32_t... a_tail, uint32_t... b_tail>
struct GreaterThan<BigUnsigned<a_n, a_tail...>, BigUnsigned<b_n, b_tail...>> {
    using A_tail = BigUnsigned<a_tail...>;
    using B_tail = BigUnsigned<b_tail...>;
    static const bool value =
        GreaterThan<A_tail, B_tail>::value || (GreaterThanOrEqualTo<A_tail, B_tail>::value && a_n > b_n);
};

template<uint32_t a_n, uint32_t b_n, uint32_t... a_tail, uint32_t... b_tail>
struct GreaterThanOrEqualTo<BigUnsigned<a_n, a_tail...>, BigUnsigned<b_n, b_tail...>> {
    using A_tail = BigUnsigned<a_tail...>;
    using B_tail = BigUnsigned<b_tail...>;
    static const bool value =
        GreaterThan<A_tail, B_tail>::value || (GreaterThanOrEqualTo<A_tail, B_tail>::value && a_n >= b_n);
};

template<class A, class B>
struct LessThan {
    static const bool value = !GreaterThanOrEqualTo<A, B>::value;
};

template<class A, class B>
struct LessThanOrEqualTo {
    static const bool value = !GreaterThan<A, B>::value;
};

Итак, деление. Начнём как положено: с определения классов и задания базы рекурсии.

template<class A, class B>
struct Division;

template<class A>
struct Division<A, Zero> {
    using Quotient = DivisionByZeroError;
    using Residue  = DivisionByZeroError;
};

template<uint32_t n, uint32_t... tail>
struct Division<BigUnsigned<n, tail...>, One> {
    using Quotient = BigUnsigned<n, tail...>;
    using Residue  = Zero;
};

template<class A, class B>
struct DummyDivision {
    using Quotient = Zero;
    using Residue  = A;
};

Здесь мы ввели дополнительный класс-пустышку struct DivisionByZeroError {},
единственная функция которого — чуть-чуть скрашивать неказистую жизнь программиста,
пытающегося отладить шаблонную программу. Так, при попытке скомпилировать программу вида

int main(...) {
    ...
    std::cout << BinaryRepresentation<typename Division<One, Zero>::Quotient>::str() << std::endl;
    ...
}

clang выдаст нам предупреждение вроде

static_bignum.cpp:229:18: error: implicit instantiation of undefined template 'BinaryRepresentation<DivisionByZeroError>'

Зачем нужен загадочный класс DummyDivision, мы сейчас увидим.

Итак, сам алгоритм деления мы будем использовать самый простой (и, вероятно, довольно неэффективный). Пусть надо поделить A на B. Если A меньше B, то решение очевидно: остаток равен A, частное равно 0. (Собственно, очевидное деление и производит вспомогательный класс DummyDivision.) В противном случае пусть Q — это результат деления A на 2B, а R — остаток от этого деления, то есть A = 2BQ + R. Тогда, очевидно, A / B = 2Q + R / B; однако, поскольку R гарантированно меньше 2B, то R / B равно либо 0, либо 1. В свою очередь, A % B = R % B, а R % B равно либо R, либо R - B. Собственно, код:

template<uint32_t a_n, uint32_t b_n, uint32_t... a_tail, uint32_t... b_tail>
struct Division<BigUnsigned<a_n, a_tail...>, BigUnsigned<b_n, b_tail...>> {
private:
    using A = BigUnsigned<a_n, a_tail...>; // короткие имена для удобства и т.д. и т.п.
    using B = BigUnsigned<b_n, b_tail...>;
    using D = typename std::conditional<   // шаг рекурсии: делим на 2B
        GreaterThanOrEqualTo<A, B>::value,
        Division<A, typename SmallShiftLeft<B, 1>::Result>,
        DummyDivision<A, B>                // (или не делим)
    >::type;
    using Q = typename D::Quotient;  // достаём результаты
    using R = typename D::Residue;
public:
    using Quotient = typename Sum<   // складываем 2Q (что, как известно, равно Q << 1) и R / B
        typename SmallShiftLeft<Q, 1>::Result,
        typename std::conditional<GreaterThanOrEqualTo<R, B>::value, One, Zero>::type
        // спасибо <type_traits> за std::conditional, который
        // есть не что иное, как тернарный оператор над типами
    >::Result;
    using Residue = typename std::conditional<
        GreaterThanOrEqualTo<R, B>::value,
        typename Difference<R, B>::Result,
        R
    >::type;
};

Иииии наконец десятичное представление! Понятно, что для печати десятичного представления числа можно долго делить его на 10. Остаток от первого деления даст младший знак, остаток от деления первого частного на 10 даст второй знак и так далее. Однако, учтем, что в C++ мы не обязаны печатать число цифра за цифрой; нас вполне устроит поделить число с остатком, например, на 100, чтобы получить сразу два знака. Поэтому будем делить на самое большое число, влезающее в uint32_t, а именно на 10⁹.

template<class A> struct DecimalRepresentation;

template<>
struct DecimalRepresentation<Zero> {
    static inline std::string str(void) {
        return "0";
    }
};

template<class A> struct Digit; // тип, достающий младшее слово из длинного числа
template<> struct Digit<Zero> {
    static const uint32_t value = 0;
};
template<uint32_t digit, uint32_t... tail>
struct Digit<BigUnsigned<digit, tail...>> {
    static const uint32_t value = digit;
};

template<uint32_t n, uint32_t... tail>
struct DecimalRepresentation<BigUnsigned<n, tail...>> {
private:
    static const uint32_t modulo = 1000000000UL;
    static const uint32_t modulo_log = 9;
    using D = Division<BigUnsigned<n, tail...>, BigUnsigned<modulo>>;
    using Q = typename D::Quotient;
    using R = typename D::Residue;
    static_assert(Digit<R>::value < modulo, "invalid division by power of 10");
public:
    static std::string str(void) {
        // гуру C++ наверняка смогут улучшить этот код, ну а до тех пор пусть лежит такой.
        // просто печатаем десятичные числа в строку, добивая их нулями.
        std::string stail = DecimalRepresentation<Q>::str(); // здесь случилась рекурсия
        if(stail == "0") stail = "";
        std::string curr = std::to_string(Digit<R>::value);  // здесь печатаем текущий остаток
        if(stail != "")
            while(curr.size() < modulo_log)
                curr = "0" + curr;
        return stail + curr;
    }
};

И вот, наконец, наш код

using A = BigUnsigned<0xFFFFFFFFULL>;
using B = One;
using C = Sum<A, B>::Result;
int main(int argc, char** argv) {
    std::cout << DecimalRepresentation<C>::str() << std::endl;

}

выдаёт 4294967296, что в точности равно 2³²!

Весь код вместе

#include <cstdint>
#include <bitset>
#include <iostream>
#include <algorithm>
#include <type_traits>

template<uint32_t... digits>
struct BigUnsigned {
    static const size_t length = sizeof...(digits);
};
using Zero = BigUnsigned< >;
using One  = BigUnsigned<1>;

template<class A, class B>
struct Concatenate {
    using Result = void;
};

template<uint32_t... a, uint32_t... b>
struct Concatenate<BigUnsigned<a...>, BigUnsigned<b...>> { // >> - не проблема для C++11
    using Result = BigUnsigned<a..., b...>;
};

template<class A, class B> struct Sum;
template<class A> struct Sum<Zero,    A> { using Result = A;    };
template<class A> struct Sum<   A, Zero> { using Result = A;    };
// если не определить этот частный случай отдельно, компилятор будет колебаться между предыдущими двумя:
template<       > struct Sum<Zero, Zero> { using Result = Zero; };

template<uint32_t a_0, uint32_t... a_tail, uint32_t b_0, uint32_t... b_tail>
struct Sum<BigUnsigned<a_0, a_tail...>, BigUnsigned<b_0, b_tail...>> {
    static const uint32_t carry = b_0 > UINT32_MAX - a_0 ? 1 : 0;
    using Result = typename Concatenate<
        BigUnsigned<a_0 + b_0>,
        typename Sum<
            typename Sum<
                BigUnsigned<a_tail...>, BigUnsigned<b_tail...>
            >::Result,
            BigUnsigned<carry>
        >::Result
    >::Result;
};

template<class A> struct BinaryRepresentation;
template<uint32_t a_0, uint32_t... a>
struct BinaryRepresentation<BigUnsigned<a_0, a...>> {
    static std::string str(void) {
        std::bitset<32> bset(a_0);
        return BinaryRepresentation<BigUnsigned<a...>>::str() + bset.to_string();
    }
};
template<>
struct BinaryRepresentation<Zero> {
    static std::string str(void) {
        return "0b"; // Oppa Python Style
    }
};

template<class A, class B> struct Difference;

struct OverflowError {};

template<> struct Difference<Zero, Zero> { using Result = Zero; };

template<uint32_t n, uint32_t... tail>
struct Difference<BigUnsigned<n, tail...>, Zero> { using Result = BigUnsigned<n, tail...>; };

template<uint32_t n, uint32_t... tail>
struct Difference<Zero, BigUnsigned<n, tail...>> { using Result = OverflowError; };

template<class A> struct Difference<OverflowError, A> { using Result = OverflowError; };
template<class A> struct Difference<A, OverflowError> { using Result = OverflowError; };

template<uint32_t a_n, uint32_t b_n, uint32_t... a_tail, uint32_t... b_tail>
struct Difference<BigUnsigned<a_n, a_tail...>, BigUnsigned<b_n, b_tail...> > {
    using A = BigUnsigned<a_n, a_tail...>; // вводим короткие имена для удобства
    using B = BigUnsigned<b_n, b_tail...>;
    using C = typename Difference<BigUnsigned<a_tail...>, BigUnsigned<b_tail...>>::Result;
    using Result_T = typename std::conditional< // есть перенос или нет?
        a_n >= b_n, C, typename Difference<C, One>::Result
    >::type;
    using Result = typename std::conditional< // убираем возможные ведущие нули
        a_n == b_n && std::is_same<Result_T, Zero>::value,
        Zero,
        typename Concatenate<
            BigUnsigned<a_n - b_n>,
            Result_T
        >::Result
    >::type;
};

template<class A, size_t shift> struct ShiftLeft;
template<class A, size_t shift> struct ShiftRight;
template<class A, size_t shift> struct BigShiftLeft;
template<class A, size_t shift> struct BigShiftRight;
template<class A, size_t shift> struct SmallShiftLeft;
template<class A, size_t shift> struct SmallShiftRight;

template<size_t shift> struct BigShiftLeft   <Zero, shift> { using Result = Zero; };
template<size_t shift> struct BigShiftRight  <Zero, shift> { using Result = Zero; };
template<size_t shift> struct SmallShiftLeft <Zero, shift> { using Result = Zero; };
template<size_t shift> struct SmallShiftRight<Zero, shift> { using Result = Zero;
    static const uint32_t carry = 0;
};
template<uint32_t... a> struct BigShiftLeft   <BigUnsigned<a...>, 0> { using Result = BigUnsigned<a...>; };
template<uint32_t... a> struct BigShiftRight  <BigUnsigned<a...>, 0> { using Result = BigUnsigned<a...>; };
template<uint32_t... a> struct SmallShiftLeft <BigUnsigned<a...>, 0> { using Result = BigUnsigned<a...>; };
template<uint32_t... a> struct SmallShiftRight<BigUnsigned<a...>, 0> { using Result = BigUnsigned<a...>;
    static const uint32_t carry = 0;
};

template<uint32_t... a, size_t shift>
struct BigShiftLeft<BigUnsigned<a...>, shift> {
    using Result = typename Concatenate<
        BigUnsigned<0>,
        typename BigShiftLeft<
            BigUnsigned<a...>,
            shift - 1
        >::Result
    >::Result;
};

template<uint32_t a_0, uint32_t... a_tail, size_t shift>
struct BigShiftRight<BigUnsigned<a_0, a_tail...>, shift> {
    using Result = typename BigShiftRight<
        BigUnsigned<a_tail...>,
        shift - 1
    >::Result;
};

template<uint32_t a_0, uint32_t... a_tail, size_t shift>
struct SmallShiftLeft<BigUnsigned<a_0, a_tail...>, shift> {
    static_assert(shift < 32, "shift in SmallShiftLeft must be less than 32 bits");
    static const uint32_t carry = a_0 >> (32 - shift);
    using Tail = typename Sum< // здесь хватило бы Or или Xor, но Sum у нас уже есть
        typename SmallShiftLeft<BigUnsigned<a_tail...>, shift>::Result,
        BigUnsigned<carry>
    >::Result;
    using Result = typename std::conditional<
        std::is_same<Tail, BigUnsigned<0>>::value, // убираем ведущие нули, если появляются (нормализация!)
        BigUnsigned<(a_0 << shift)>,
        typename Concatenate<
            BigUnsigned<(a_0 << shift)>,
            Tail
        >::Result
    >::type;
};

template<uint32_t a_0, uint32_t... a_tail, size_t shift>
struct SmallShiftRight<BigUnsigned<a_0, a_tail...>, shift> {
    static_assert(shift < 32, "shift in SmallShiftRight must be less than 32 bits");
    static const uint32_t carry = a_0 << (32 - shift);
    using Result = typename Concatenate<
        BigUnsigned<(a_0 >> shift) | SmallShiftRight<BigUnsigned<a_tail...>, shift>::carry>,
        typename SmallShiftRight<BigUnsigned<a_tail...>, shift>::Result
    >::Result;
};

template<class A, size_t shift>
struct ShiftLeft {
    using Result = typename BigShiftLeft<
        typename SmallShiftLeft<A, shift % 32>::Result,
        shift / 32
    >::Result;
};

template<class A, size_t shift>
struct ShiftRight {
    using Result = typename SmallShiftRight<
        typename BigShiftRight<A, shift / 32>::Result,
        shift % 32
    >::Result;
};

template<class A, class B> struct GreaterThan;
template<class A, class B> struct GreaterThanOrEqualTo;

template<class A> struct GreaterThan<Zero, A>             { static const bool value = false; };
template<class A> struct GreaterThanOrEqualTo<Zero, A>    { static const bool value = false; };
template<       > struct GreaterThanOrEqualTo<Zero, Zero> { static const bool value = true;  };

template<uint32_t n, uint32_t... tail>
struct GreaterThanOrEqualTo<BigUnsigned<n, tail...>, Zero> {
    static const bool value = true;
};

template<uint32_t n, uint32_t... tail>
struct GreaterThan<BigUnsigned<n, tail...>, Zero> {
    static const bool value = n > 0 || GreaterThan<BigUnsigned<tail...>, Zero>::value;
};

template<uint32_t a_n, uint32_t b_n, uint32_t... a_tail, uint32_t... b_tail>
struct GreaterThan<BigUnsigned<a_n, a_tail...>, BigUnsigned<b_n, b_tail...>> {
    using A_tail = BigUnsigned<a_tail...>;
    using B_tail = BigUnsigned<b_tail...>;
    static const bool value =
        GreaterThan<A_tail, B_tail>::value || (GreaterThanOrEqualTo<A_tail, B_tail>::value && a_n > b_n);
};

template<uint32_t a_n, uint32_t b_n, uint32_t... a_tail, uint32_t... b_tail>
struct GreaterThanOrEqualTo<BigUnsigned<a_n, a_tail...>, BigUnsigned<b_n, b_tail...>> {
    using A_tail = BigUnsigned<a_tail...>;
    using B_tail = BigUnsigned<b_tail...>;
    static const bool value =
        GreaterThan<A_tail, B_tail>::value || (GreaterThanOrEqualTo<A_tail, B_tail>::value && a_n >= b_n);
};

template<class A, class B>
struct LessThan {
    static const bool value = !GreaterThanOrEqualTo<A, B>::value;
};

template<class A, class B>
struct LessThanOrEqualTo {
    static const bool value = !GreaterThan<A, B>::value;
};

struct DivisionByZeroError { };

template<class A, class B>
struct Division;

template<class A>
struct Division<A, Zero> {
    using Quotient = DivisionByZeroError;
    using Residue  = DivisionByZeroError;
};

template<uint32_t n, uint32_t... tail>
struct Division<BigUnsigned<n, tail...>, One> {
    using Quotient = BigUnsigned<n, tail...>;
    using Residue  = Zero;
};

template<class A, class B>
struct DummyDivision {
    using Quotient = Zero;
    using Residue  = A;
};

template<uint32_t a_n, uint32_t b_n, uint32_t... a_tail, uint32_t... b_tail>
struct Division<BigUnsigned<a_n, a_tail...>, BigUnsigned<b_n, b_tail...>> {
private:
    using A = BigUnsigned<a_n, a_tail...>;
    using B = BigUnsigned<b_n, b_tail...>;
    using D = typename std::conditional<
        GreaterThanOrEqualTo<A, B>::value,
        Division<A, typename SmallShiftLeft<B, 1>::Result>,
        DummyDivision<A, B>
    >::type;
    using Q = typename D::Quotient;
    using R = typename D::Residue;
public:
    using Quotient = typename Sum<
        typename SmallShiftLeft<Q, 1>::Result,
        typename std::conditional<GreaterThanOrEqualTo<R, B>::value, One, Zero>::type
    >::Result;
    using Residue = typename std::conditional<
        GreaterThanOrEqualTo<R, B>::value,
        typename Difference<R, B>::Result,
        R
    >::type;
};

template<class A> struct DecimalRepresentation;

template<>
struct DecimalRepresentation<Zero> {
    static inline std::string str(void) {
        return "0";
    }
};

template<class A> struct Digit;
template<> struct Digit<Zero> {
    static const uint32_t value = 0;
};
template<uint32_t digit, uint32_t... tail>
struct Digit<BigUnsigned<digit, tail...>> {
    static const uint32_t value = digit;
};

template<uint32_t n, uint32_t... tail>
struct DecimalRepresentation<BigUnsigned<n, tail...>> {
private:
    static const uint32_t modulo = 1000000000UL;
    static const uint32_t modulo_log = 9;
    using D = Division<BigUnsigned<n, tail...>, BigUnsigned<modulo>>;
    using Q = typename D::Quotient;
    using R = typename D::Residue;
    static_assert(Digit<R>::value < modulo, "invalid division by power of 10");
public:
    static std::string str(void ){
        std::string stail = DecimalRepresentation<Q>::str();
        if(stail == "0") stail = "";
        std::string curr = std::to_string(Digit<R>::value);
        if(stail != "")
            while(curr.size() < modulo_log)
                curr = "0" + curr;
        return stail + curr;
    }
};

using A = BigUnsigned<0xFFFFFFFFULL>;
using B = One;
using C = Sum<A, B>::Result;
int main(int argc, char** argv) {
    std::cout << DecimalRepresentation<C>::str() << std::endl;

}

Что ещё необходимо сказать

Во-первых, нельзя сказать, что на этом наша длинная арифметика готова. Мы могли
бы добавить сюда много: умножение (столбиком), возведение в степень, даже алгоритм
Евклида. Несложно придумать, как определить класс BigSigned<int, uint32_t...>
длинных чисел со знаком и все основные операции на нём.

Во-вторых, баги. Весь код приведён в учебных целях и, вероятно, нуждается в отладке.
(Я отлаживал версию, появившуюся до шаблонов с переменным аргументом, и, к сожалению,
только на одном компиляторе.) Будем надеяться, что хотя бы учебные цели были достигнуты.

В-третьих, нужно признать, что длинная арифметика — далеко не идеальный пример
для демонстрации силы шаблонов с переменным аргументом. Если вы видели интересные и практичные примеры использования этой фичи — пожалуйста, делитесь ссылками в комментариях.

Теги:

Хабы:

Если эта публикация вас вдохновила и вы хотите поддержать автора — не стесняйтесь нажать на кнопку

C++11 variadic templates и длинная арифметика на этапе компиляции

Parameter packs

Длинная арифметика

Что ещё необходимо сказать

Публикации

Истории

Работа

Ближайшие события