Анализ открытых данных в R, часть 1

Введение

На момент написания статьи большинство приложений на основе открытых данных (на официальных сайтах data.mos.ru/apps и data.gov.ru) представляют собой интерактивные справочники по инфраструктуре города или поселения с наглядной визуализацией и часто с опцией выбора оптимального маршрута. Цель этой и последующих публикаций состоит в том, чтобы привлечь внимание сообщества к обсуждению стратегий анализа открытых данных, в т.ч. направленных на прогнозирование, построение статистических моделей и извлечение информации, не представленной в явном виде. В качестве инструментария используется язык R и среда разработки RStudio.

В качестве иллюстрации простоты использования R рассмотрим небольшой пример и визуализируем на карте реестр привлечения УК, ТСЖ за 2013 год в Ульяновске. В этом наборе данных содержится информация о штрафах различных управляющих компаний. Для визуализации выбрано количество устных замечаний, количество штрафов и штрафы в рублях за все представленное в датасете время. Этим данным(как и всем другим из открытых источников, что мне попадались) свойственно иметь много пропусков, опечаток, и т.д. поэтому в R загружаются предобработанные данные:

ulyanovsk.data <- read.csv('./data/formated_tsj.csv')


Для визуализации используется интерфейс к google maps и библиотека ggplot2, для организации графиков на устройстве вывода используется gridExtra:

Код

library(ggmap)
library(ggplot2)
library(gridExtra)

В датасете есть столбцы lat и lon, в которых содержится информация о широте и долготе. Нам нужна карта не всего Ульяновска а только его части, координаты которой находятся в выборке:

Код

box < — make_bbox(lon, lat, data = ulyanovsk.data)
ulyanovsk.map < — get_map(location = 'ulyanovsk', zoom=calc_zoom(box))
p0 < — ggmap(ulyanovsk.map)
p0 < — p0 + ggtitle(«Часть карты Ульяновска») + theme(legend.position=«none»)

Наносим на карту штрафы в рублях(солбец penalties_rub_total):

Код

p1 < — ggmap(ulyanovsk.map)
p1 < — p1 + geom_point(data = ulyanovsk.data, aes(x = lon, y = lat, color = penalties_rub_total, size = penalties_rub_total))
p1 < — p1 + scale_color_gradient(low = 'yellow', high = 'red')
p1 < — p1 + ggtitle(«Штрафы, в рублях») + theme(legend.position=«none»)

Число штрафов в штуках:

Код

p2 < — ggmap(ulyanovsk.map)
p2 < — p2 + geom_point(data = ulyanovsk.data, aes(x = lon, y = lat, color = penalties_total, size = penalties_total))
p2 < — p2 + scale_color_gradient(low = 'yellow', high = 'red')
p2 < — p2 + ggtitle(«Кол-во штрафов») + theme(legend.position=«none»)

Число устных замечаний в штуках:

Код

p3 < — ggmap(ulyanovsk.map)
p3 < — p3 + geom_point(data = ulyanovsk.data, aes(x = lon, y = lat, color = oral_comments_total, size = oral_comments_total))
p3 < — p3 + scale_color_gradient(low = 'yellow', high = 'red')
p3 < — p3 + ggtitle(«Кол-во устных замечаний») + theme(legend.position=«none»)

Строим все вместе:

grid.arrange(p0, p1, p2, p3, ncol=2)




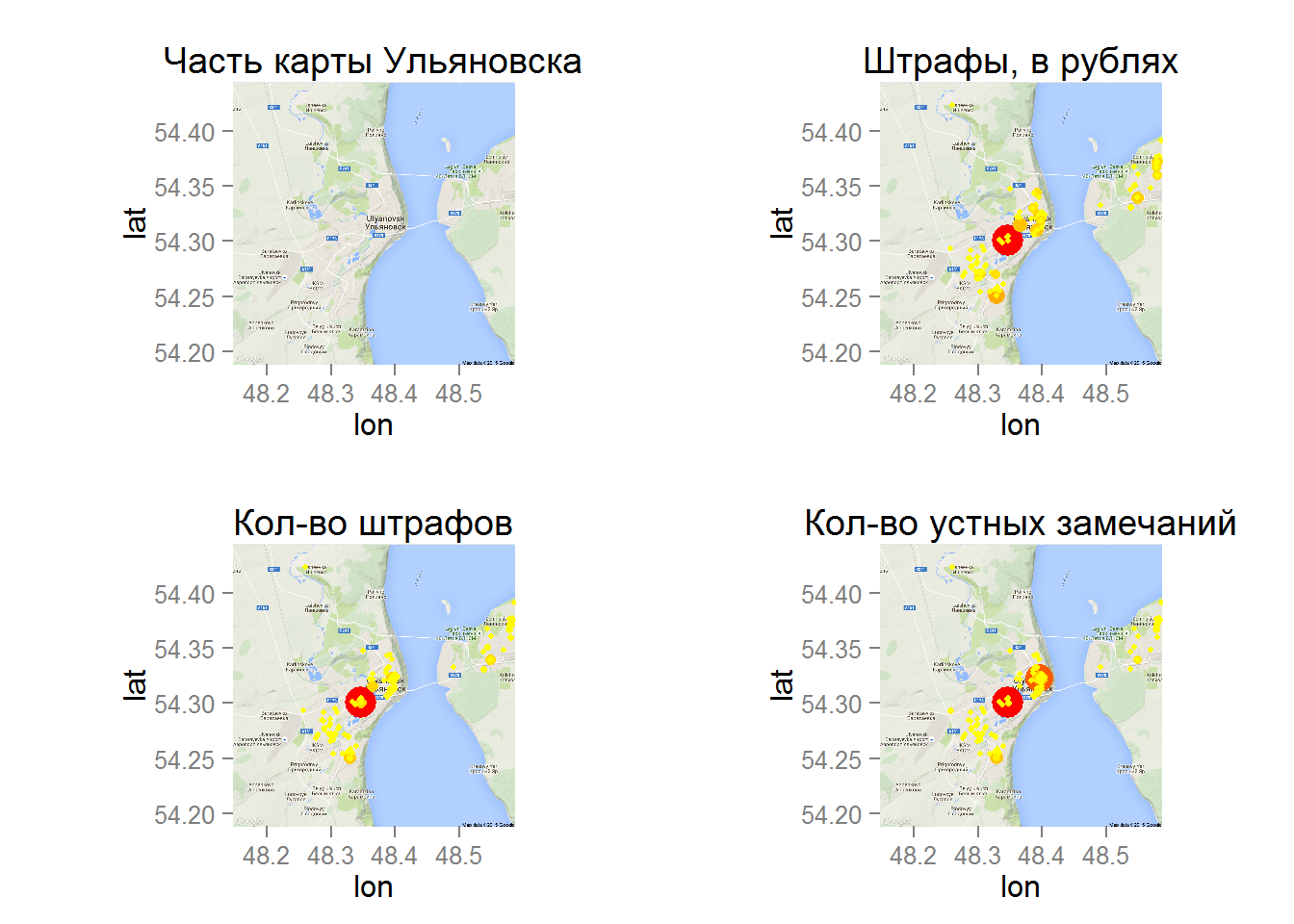
Размер точки и величина красного монотонно возрастают с параметром(например, чем больше штрафов, тем точка больше и краснее). По графикам видно, что в исследуемом датасете управляющие компании с правого берега Ульяновска имеют большее число штрафов и замечаний, чем с левого.

Исследование статистики ДТП

В этом разделе использованы данные единой межведомственной информационно-статистической системы. В датасете содержится показатель смертности от ДТП на 100 тыс. человек по регионам РФ за 2011-2014 год:

Код

accidents < — read.csv('./data/accidents.csv')
head(accidents)

Среднее для каждого года по областям:

apply(accidents[,2:5],2,FUN = mean)


## y2011 y2012 y2013 y2014
## 21.36942 21.55694 20.18582 20.34727

Гистограммы:

Код

library(reshape2)
accidents.melt < — melt(accidents[,2:5])
ggplot(accidents.melt, aes(x = value, fill = variable)) + geom_histogram(alpha = 0.3)

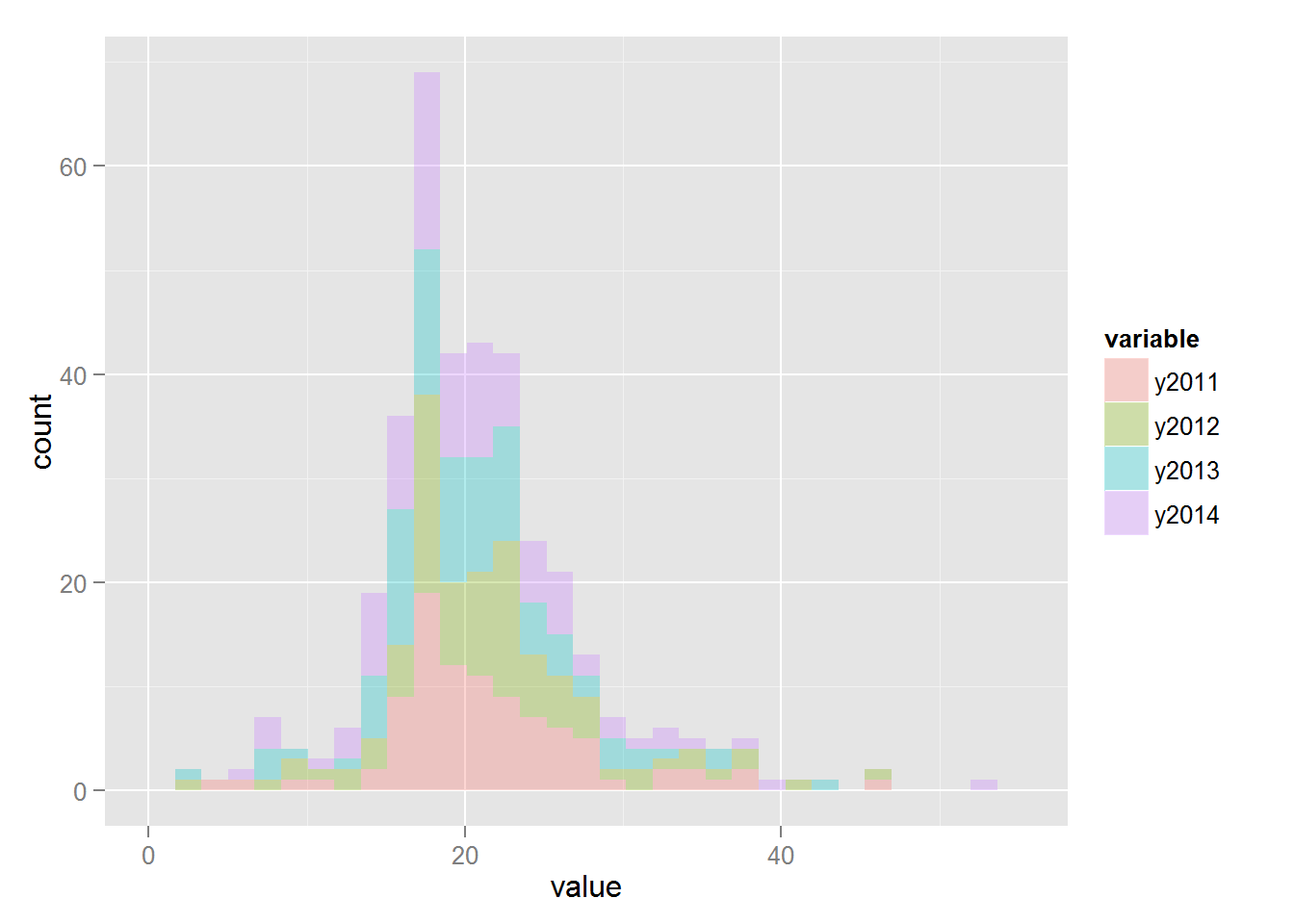
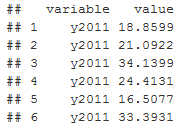
Функция melt реорганизует датасет таким образом, что в столбце value хранится значение показателя, в столбце variable год, за который показатель был получен:

head(accidents.melt)




Интересно сравнить, является ли статистически значимым различие показателей для разных лет. Принимаются следующие модельные предположения:

1) Значение показателя является случайной величиной, подчиняющейся распределению Стьюдента
2) Для каждого года имеются свои параметры распределения, nu — параметр нормальности, sigma — дисперсия, mu — среднее
3) Параметры nu, sigma, mu так же являются случайными величинами, со своими распределениями, не зависящими от года

Формальная постановка задачи: используя данные установить, являются ли параметр распределения mu для разных лет разным. Если выписать для нашего случая формулу Байеса(которую я не буду тут приводить, чтобы не загромождать статью), то получается иерархическая модель:

1) показатель смертности (поле value в accidents.melt) ~ t(mu,sigma,nu)
2) mu | group_id ~ N(mu_hyp, sigma_hyp )
3) sigma | group_id ~ Unif(a_hyp, b_hyp | group_id)
4) nu | group_id ~ Exp(lambda_hyp)

Где mu | group_id ~ N(mu_hyp, sigma_hyp ) обозначает, что параметр mu для группы group_id имеет нормальное распределение с гиперпараметрами mu_hyp, sigma_hyp.
Переменная group_id принимает значение в зависимости от года, 1 для 2011, 2 для 2012 и т.д.:

accidents.melt$group_id <- as.numeric(accidents.melt$variable)


Для моделирования в R используется интерфейс к языку Jags и вспомогательная функция plotPost из файла DBDA2E-utilities.R, который можно найти здесь(автор — John Kruschke):

Код

library(rjags)
source('DBDA2E-utilities.R')

Описание модели происходит на языке jags, поэтому сначала создается файл или строковая переменная внутри R с моделью:

Код

modelString < — '

model {

for(i in 1:N)
{

y[i] ~ dt(mu[group_id[i]], 1/sigma[group_id[i]]^2, nu[group_id[i]])

}

for(j in 1:NumberOfGroups)
{

mu[j] ~ dnorm(PriorMean, 0.01)
sigma[j] ~ dunif(1E-1, 1E+1)
nuTemp[j] ~ dexp(1/19)
nu[j] < — nuTemp[j] + 1

}

}

'

После того, как модель специфицирована, она передается jags вместе с данными:

Код

modelJags < — jags.model(file = textConnection(modelString),
data = list(y = accidents.melt$value, group_id = accidents.melt$group_id, N = length(accidents.melt), NumberOfGroups = 4, PriorMean = (20)),
n.chains = 8, n.adapt = 1000)

Jags использует MCMC и реализует модель случайных блужданий в пространстве наших параметров mu, sigma, nu. Причем вероятность того, что параметры примут конкретное значение пропорциональна их совместной вероятности, хотя совместная вероятность не считается в явном виде. Таким образом jags возвращает список значений mu, sigma, nu, поэтому можно оценить их вероятности используя гистограммы. Следующие строки запускают нашу модель и возвращают результат:

Код

update(modelJags,2000)
summary(samplesCoda < — coda.samples(model = modelJags, variable.names = c('nu','mu','sigma'), n.iter = 50000, thin = 500))

Для ответа на наш вопрос о значении параметра mu для разных лет рассмотрим гистограммы разности значений параметров:

Код

samplesCodaMatrix < — as.matrix(samplesCoda)
samplesCodaDataFrame < — as.data.frame(samplesCodaMatrix)
samplesCodaDataFrame < — samplesCodaDataFrame[,1:4]
plotPost(samplesCodaMatrix[,1]- samplesCodaMatrix[,2], cenTend = 'mean', main = '2011 vs. 2012')
plotPost(samplesCodaMatrix[,1]- samplesCodaMatrix[,3], cenTend = 'mean', main = '2011 vs. 2013')
plotPost(samplesCodaMatrix[,1]- samplesCodaMatrix[,4], cenTend = 'mean', main = '2011 vs. 2014')
plotPost(samplesCodaMatrix[,2]- samplesCodaMatrix[,3], cenTend = 'mean', main = '2012 vs. 2013')
plotPost(samplesCodaMatrix[,2]- samplesCodaMatrix[,4], cenTend = 'mean', main = '2012 vs. 2014')
plotPost(samplesCodaMatrix[,3]- samplesCodaMatrix[,4], cenTend = 'mean', main = '2013 vs. 2014')

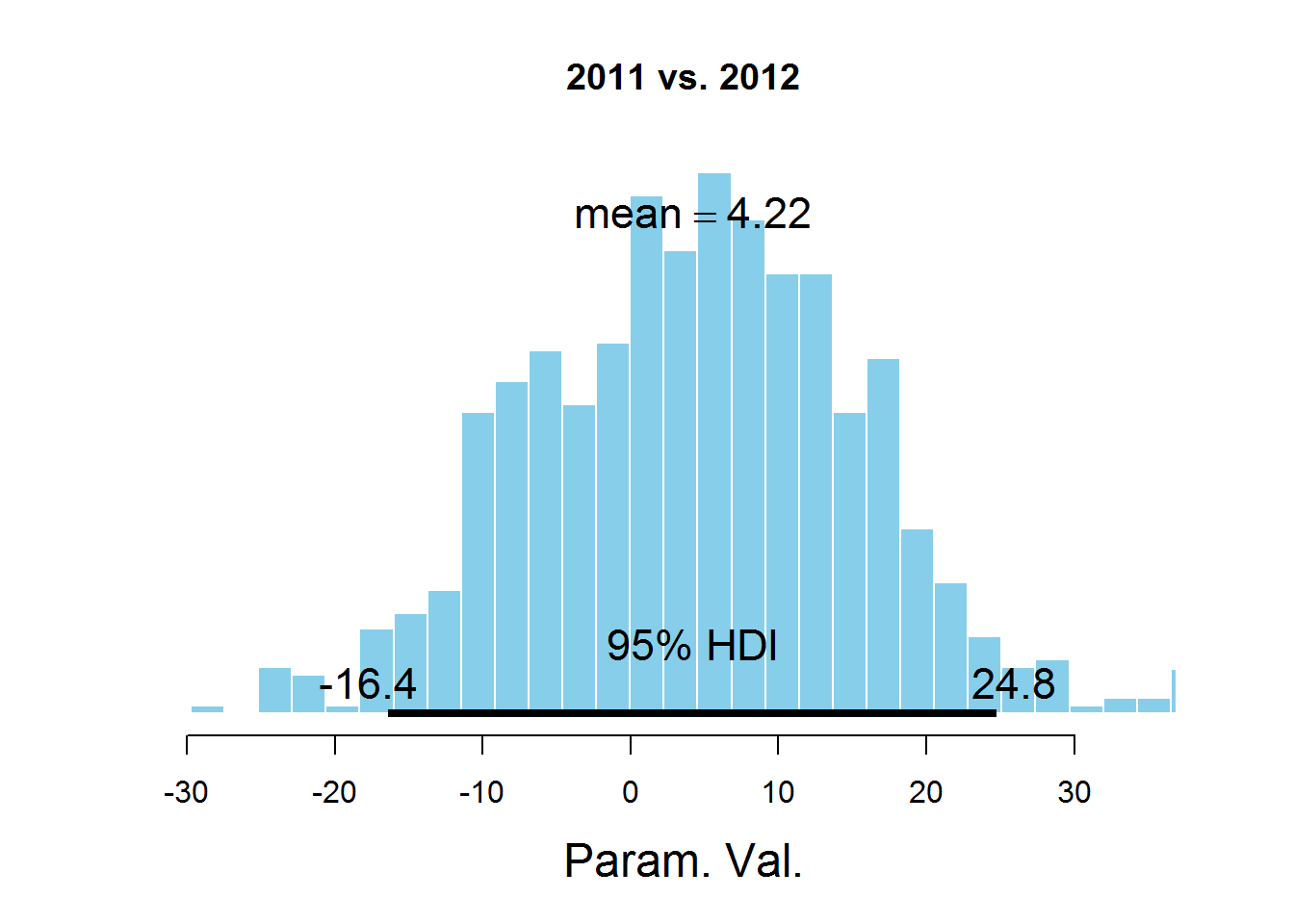
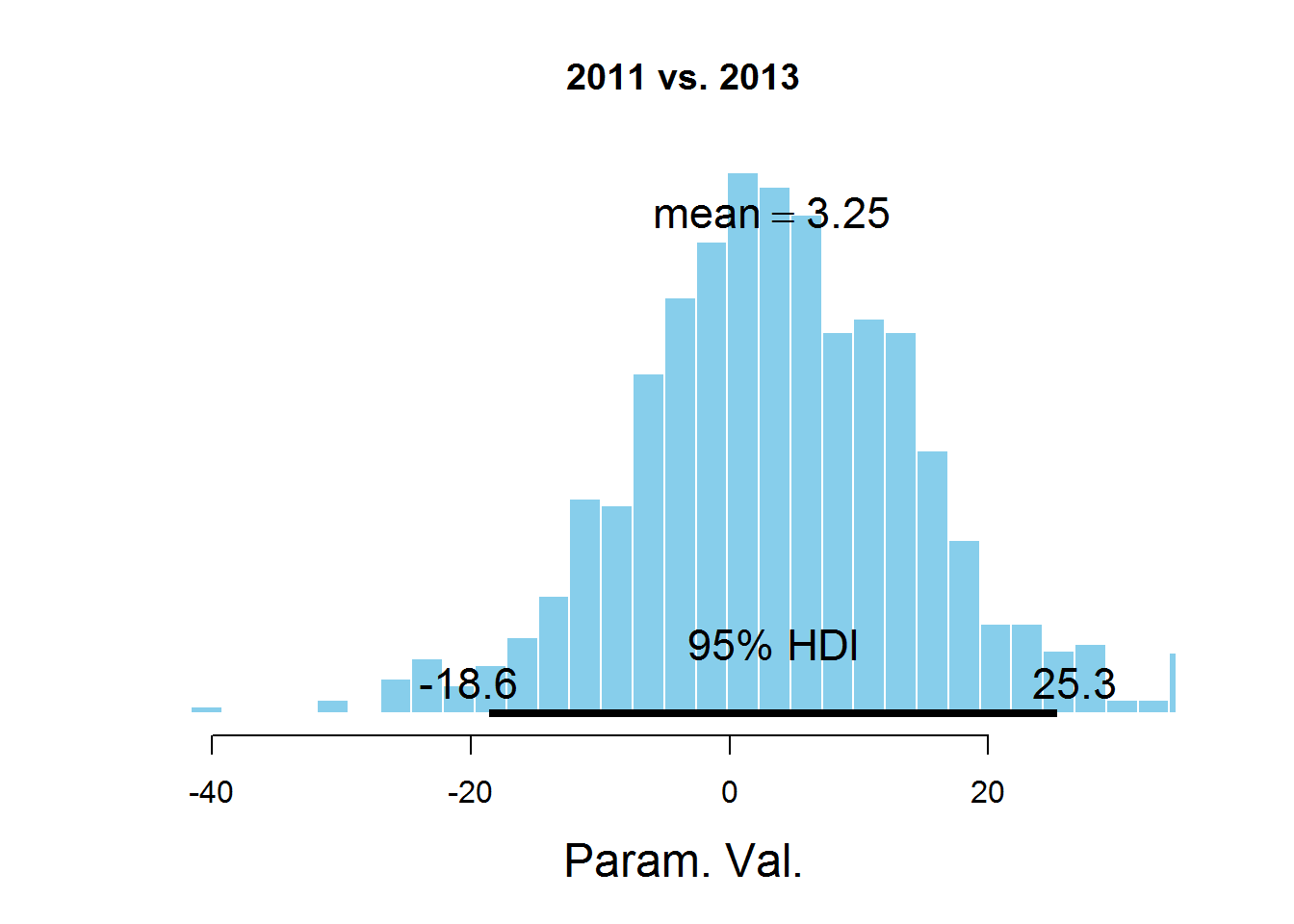
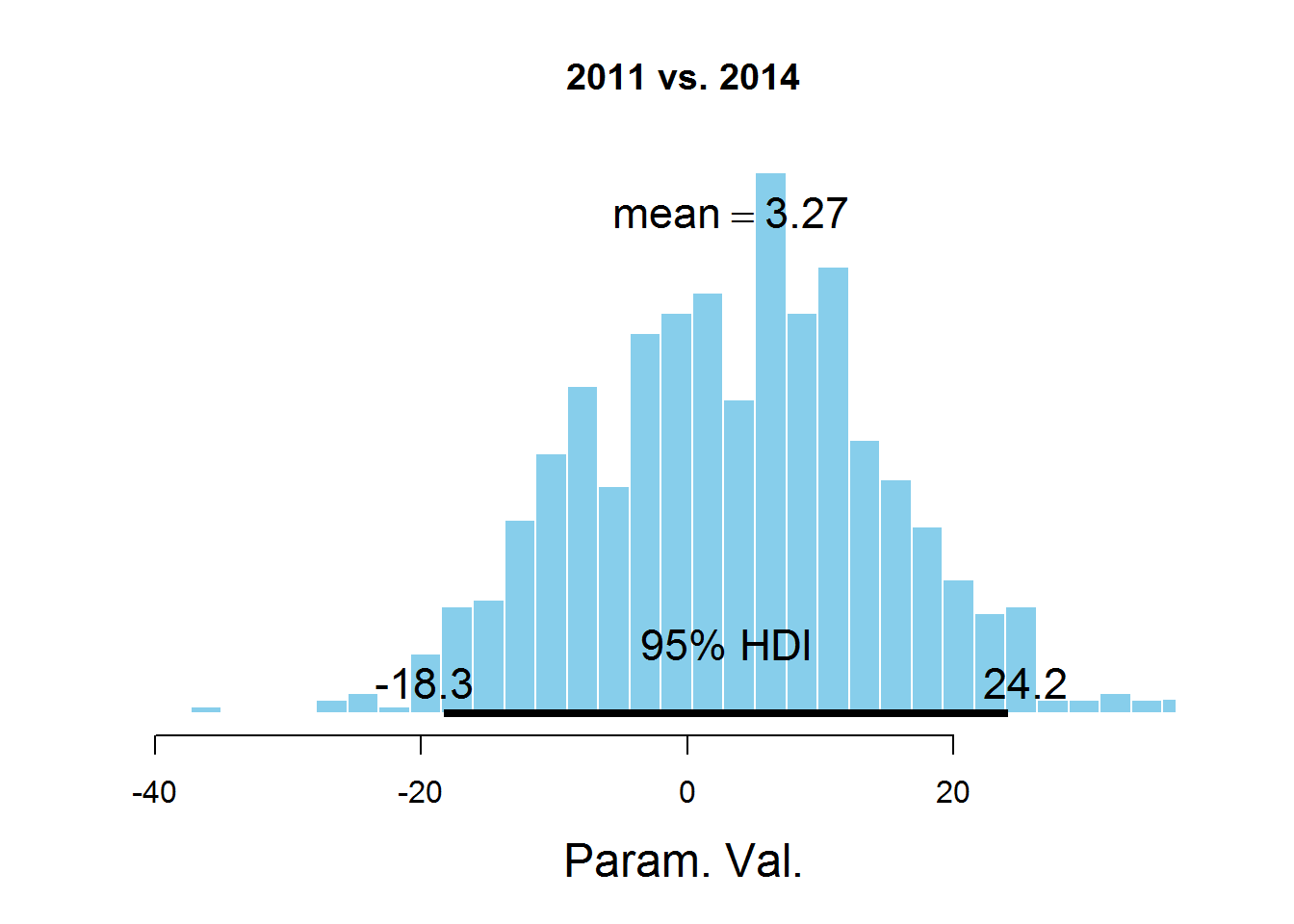
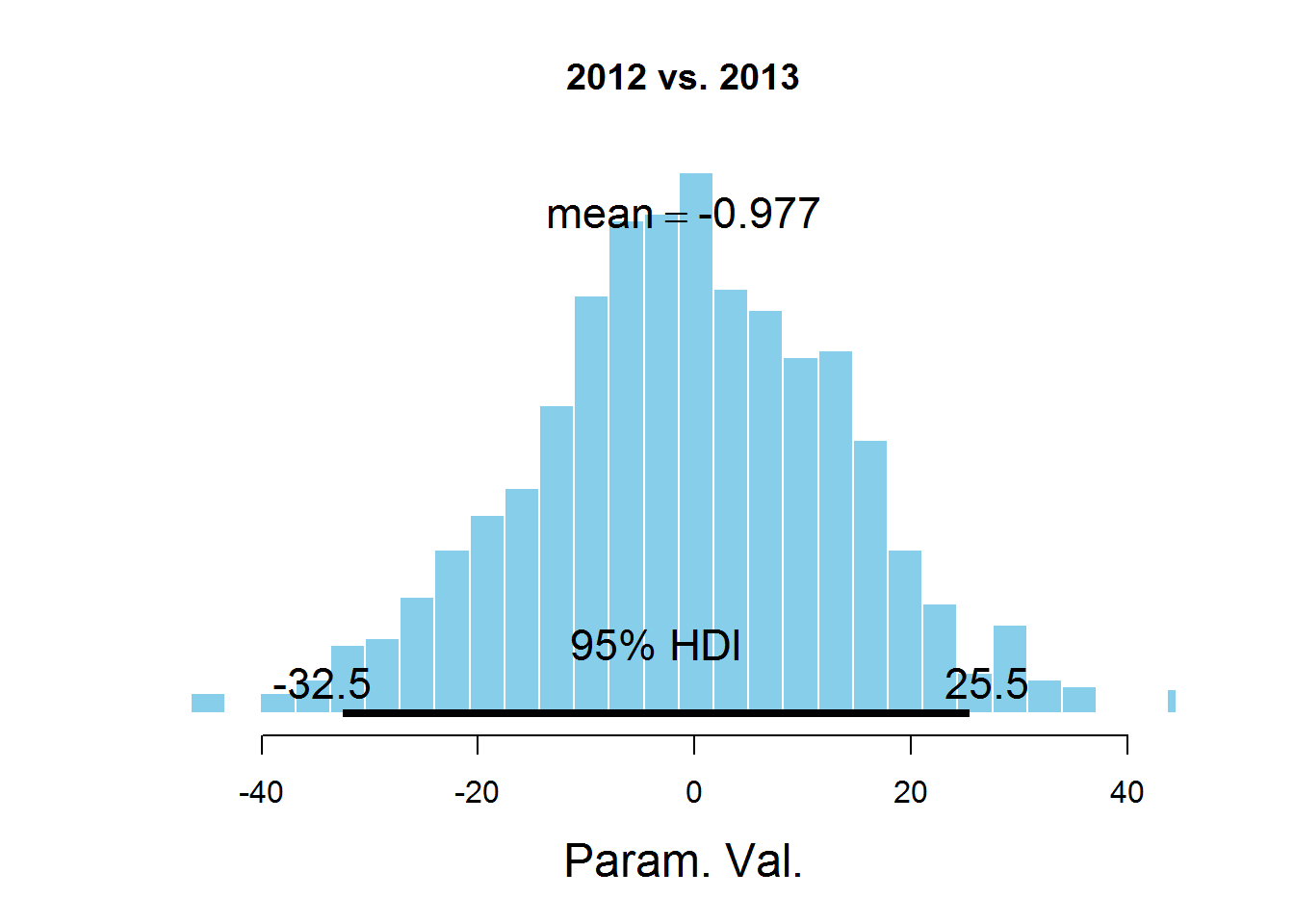
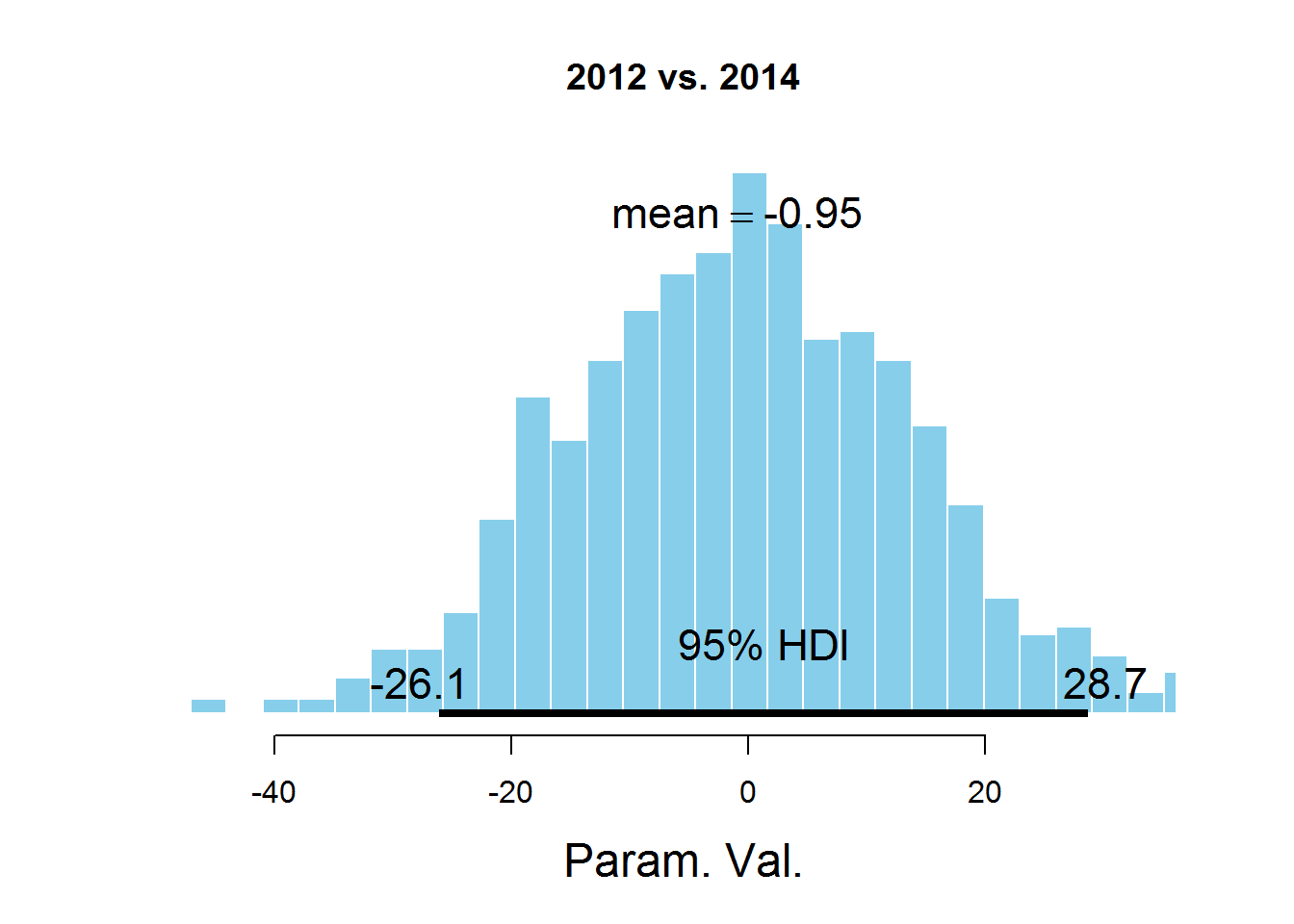
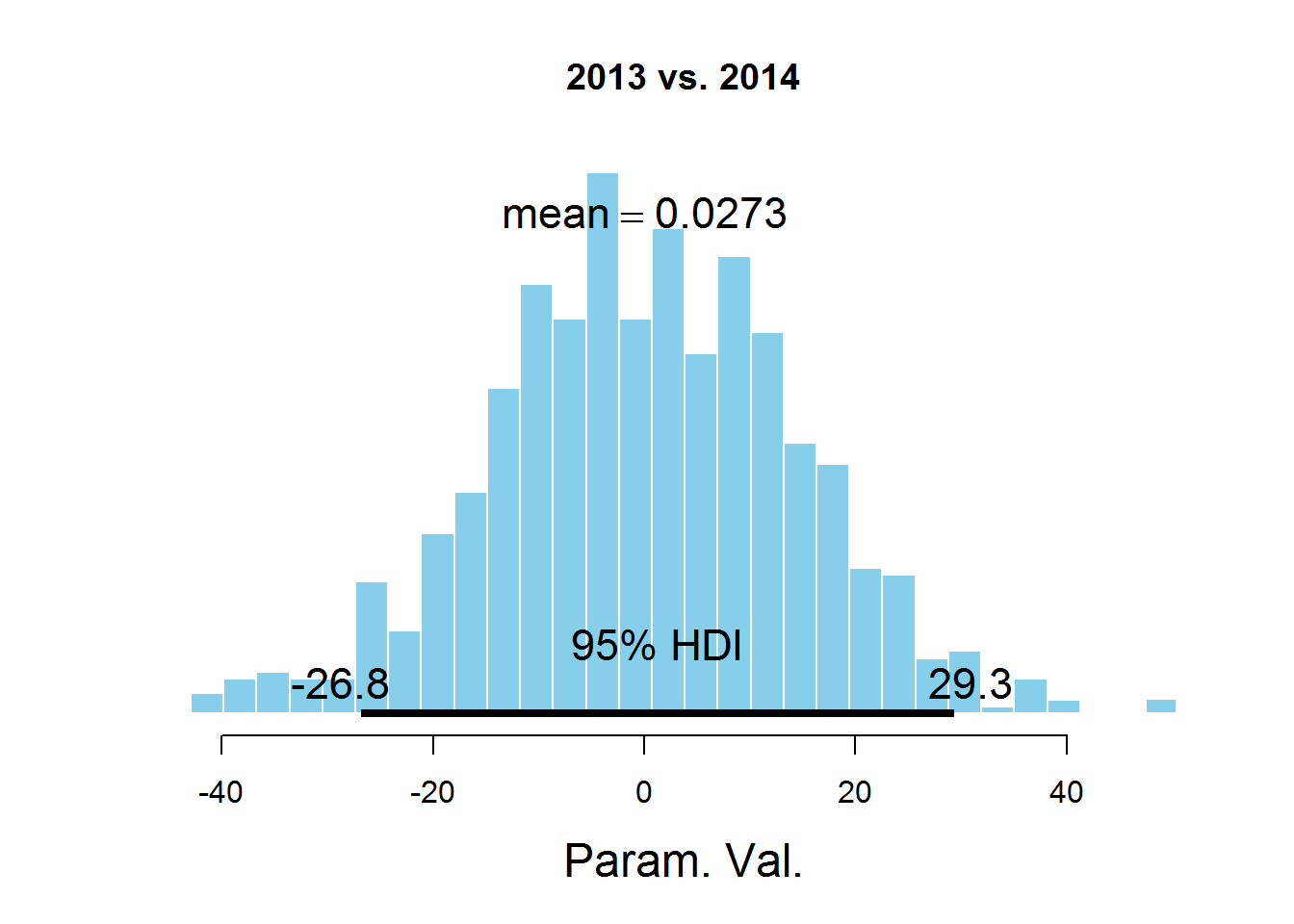
На графиках обозначен HDI интервал, значения в котором имеют бОльшую вероятность, чем значения вне интервала, а сумма вероятностей этих значений равна 0,95. Видно, что значение 0 попадает в HDI, что дает основание предположить, что параметр mu один и тот же для всех представленных в датасете лет. Здесь есть спорный момент — значение HDI подбирается согласно знанию предметной области, т.е. возможно для этой задачи значение 95% не самое подходящее.