Традиционная техника “начального уровня”, сравнения текущего изображения с эталоном основывается на рассмотрении изображений как двумерных функций яркости (дискретных двумерных матриц интенсивности). При этом измеряется либо расстояние между изображениями, либо мера их близости.
Как правило, для вычисления расстояний между изображениями используется формула, являющаяся суммой модулей или квадратов разностей интенсивности:
Если помимо простого сравнения двух изображений требуется решить задачу обнаружения позиции фрагмента одного изображения в другом, то классический метод “начального уровня”, заключающийся в переборе всех координат и вычисления расстояния по указанной формуле, как правило, терпит неудачу практического использования из-за требуемого большого количества вычислений.
Одним из методов, позволяющих значительно сократить количество вычислений, является применение Фурье преобразований и дискретных Фурье преобразований для расчёта меры совпадения двух изображений при различных смещениях их между собой. Вычисления при этом происходят одновременно для раз��ичных комбинаций сдвигов изображений относительно друг друга.
Наличие большого числа библиотек, реализующих Фурье преобразований (во всевозможных вариантах быстрых версий), делает реализацию алгоритмов сравнения изображений не очень сложной задачей для программирования.
Например, найти:


Согласно определению, корреляцией <F,G> двух функций F и G называется величина:
Эта величина хорошо известна из курса математики и геометрии, посвященного линейным пространствам, где носит название скалярного произведения. Будем использовать в качестве меры между изображениями формулу:
или
Данная величина получена из операции скалярного произведения векторов (рассматривая изображения как векторы в многомерном пространстве). И даже более — эта же формула представляет собой и стандартную статистическую формулу критерия для гипотезы о совпадении двух вероятностных распределений.
Примечание:
При вычислении корреляции между фрагментами изображений, если одно изображение меньше другого, будем делить только на значение норм у пересекающийся частей.
Согласно определению, свёрткой двух функций F и G называется функция FхG:
Пусть G’(t) = G(-t) и F’(t) = F(-t), тогда, очевидна справедливость равенств:
Так же очевидно, что FхG’(t) равна корреляции получаемой в результате сдвига одного вектора, относительно другого на шаг t (это легко проверить явной подстановкой значений в формулу корреляции).
Преобразование Фурье (ℱ) — операция, сопоставляющая одной функции вещественной переменной другую функцию, также вещественной переменной. Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие — гармонические колебания с разными частотами.
Преобразование Фурье функции f вещественной переменной является интегральным и задаётся следующей формулой:
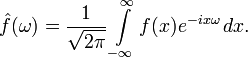
Разные источники могут давать определения, отличающиеся от приведённого выше выбором коэффициента перед интегралом, а также знака «−» в показателе эксп��ненты. Но все свойства будут те же, хотя вид некоторых формул может измениться.
Кроме того, существуют разнообразные обобщения данного понятия.
Преобразование Фурье функций, заданных на пространстве ℝ^n, определяется формулой:
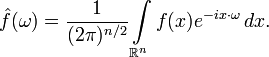
Обратное преобразование в этом случае задается формулой:
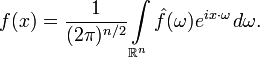
Как и прежде, в разных источниках определения многомерного преобразования Фурье могут отличаться выбором константы перед интегралом.
Дискретное преобразование Фурье (в англоязычной литературе DFT, Discrete Fourier Transform) — это одно из преобразований Фурье, широко применяемых в алгоритмах цифровой обработки сигналов (его модификации применяются в сжатии звука в MP3, сжатии изображений в JPEG и др.), а также в других областях, связанных с анализом частот в дискретном (к примеру, оцифрованном аналоговом) сигнале. Дискретное преобразование Фурье требует в качестве входа дискретную функцию. Такие функции часто создаются путём дискретизации (выборки значений из непрерывных функций). Дискретные преобразования Фурье помогают решать дифференциальные уравнения в частных производных и выполнять такие операции, как свёртки. Дискретные преобразования Фурье также активно используются в статистике, при анализе временных рядов. Существуют многомерные дискретные преобразования Фурье.
Прямое преобразование:
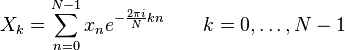
Обратное преобразование:
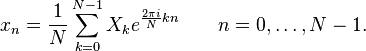
Дискретное преобразование Фурье является линейным преобразованием, которое переводит вектор временных отсчётов в вектор спектральных отсчётов той же длины. Таким образом преобразование может быть реализовано как умножение симметричной квадратной матрицы на вектор:
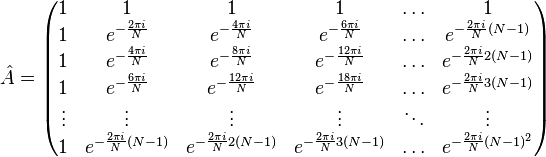
Одним из замечательных свойств преобразований Фурье является возможность быстрого вычисления корреляции двух функций определённых, либо на действительном аргументе (при использовании классической формулы), либо на конечном кольце (при использовании дискретных преобразований).
И хотя подобные свойства присущи многим линейным преобразованиям, для практического применения, для вычисления операции свёртки, согласно данному нами определению, используется формула
Где
Проверить правильность равенства довольно легко – явно подставив в формулы Фурье-преобразований и сократив получившиеся формулы
Пусть <F,G>(t) равна корреляции получаемой в результате сдвига одного вектора, относительно другого на шаг t
Тогда, как уже показано ранее, выполняется
Если используются реализации алгоритма трансформации Фурье через комплексные числа, то такие преобразования обладают ещё одним замечательным свойством:
Где CONJUGATE ( FFT(G) ) – матрица, составленная из сопряжённых элементов матрицы FFT(G)
Таким образом, получаем
При использовании формулы для оценки расстояния между изображениями при сдвиге (i,j) относительно друг друга
получаем, что
Где
При решении задачи для поиска одного образца, дополнительное нормирование образца является излишним, а также вычисление нормы у общей части может быть заменено на сумму яркостей пикселей в этой общей части или на сумму квадратов яркостей в этой общей части
При использовании формулы для оценки расстояния между изображениями при сдвиге (i,j) относительно друг друга
получаем, что
Где
Примечание:
При использовании дискретного преобразования Фурье, матрица M содержит также элементы от циклического сдвига изображений между собой. Поэтому, если не требуется анализировать циклический сдвиг кадров, то поиск максимального элемента в матрице M нужно ограничить областью (0,0)-(N1-M1, N2-M2).
Реализованные алгоритмы являются частью библиотеки с открытым исходным кодом FFTTools. Интернет-адрес: github.com/dprotopopov/FFTTools
Используемое программное обеспечение

Как правило, для вычисления расстояний между изображениями используется формула, являющаяся суммой модулей или квадратов разностей интенсивности:
d(X,Y) = SUM ( X[i,j] — Y[i,j] )^2
Если помимо простого сравнения двух изображений требуется решить задачу обнаружения позиции фрагмента одного изображения в другом, то классический метод “начального уровня”, заключающийся в переборе всех координат и вычисления расстояния по указанной формуле, как правило, терпит неудачу практического использования из-за требуемого большого количества вычислений.
Одним из методов, позволяющих значительно сократить количество вычислений, является применение Фурье преобразований и дискретных Фурье преобразований для расчёта меры совпадения двух изображений при различных смещениях их между собой. Вычисления при этом происходят одновременно для раз��ичных комбинаций сдвигов изображений относительно друг друга.
Наличие большого числа библиотек, реализующих Фурье преобразований (во всевозможных вариантах быстрых версий), делает реализацию алгоритмов сравнения изображений не очень сложной задачей для программирования.
Постановка задачи
- Пусть даны два изображения X и Y – изображение и образец, размеров (N1,N2) и (M1,M2) соответственно и Ni > Mi
- Требуется найти координаты образца Y в полном изображении X и вычислить оценочную величину — меру близости.
Например, найти:
образец

в изображении

Корреляция как мера между изображениями
Согласно определению, корреляцией <F,G> двух функций F и G называется величина:
<F,G> = SUM F(i)*G(i)
Эта величина хорошо известна из курса математики и геометрии, посвященного линейным пространствам, где носит название скалярного произведения. Будем использовать в качестве меры между изображениями формулу:
m(X,Y) = SUM ( X[i,j] * Y[i,j] ) / ( SQRT ( SUM X[i,j] ^2 ) * SQRT ( SUM Y[i,j] ^2 ) )
или
m(X,Y) = <X,Y> / ( SQRT (<X,X> ) * SQRT (<Y,Y> ) )
Данная величина получена из операции скалярного произведения векторов (рассматривая изображения как векторы в многомерном пространстве). И даже более — эта же формула представляет собой и стандартную статистическую формулу критерия для гипотезы о совпадении двух вероятностных распределений.
Примечание:
При вычислении корреляции между фрагментами изображений, если одно изображение меньше другого, будем делить только на значение норм у пересекающийся частей.
Свёртка двух функций
Согласно определению, свёрткой двух функций F и G называется функция FхG:
FхG(t) = SUM F(i)*G(j)|i+j=t
Пусть G’(t) = G(-t) и F’(t) = F(-t), тогда, очевидна справедливость равенств:
- FхF’(0) = SUM F(i)^2 – скалярное произведение вектора F на самого себя
- GхG’(0) = SUM G(j)^2– скалярное произведение вектора G на самого себя
- FхG’(0) = SUM F(i)*G(i) – скалярное произведение двух векторов F и G
Так же очевидно, что FхG’(t) равна корреляции получаемой в результате сдвига одного вектора, относительно другого на шаг t (это легко проверить явной подстановкой значений в формулу корреляции).
Преобразование Фурье
Преобразование Фурье (ℱ) — операция, сопоставляющая одной функции вещественной переменной другую функцию, также вещественной переменной. Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие — гармонические колебания с разными частотами.
Преобразование Фурье функции f вещественной переменной является интегральным и задаётся следующей формулой:
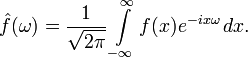
Разные источники могут давать определения, отличающиеся от приведённого выше выбором коэффициента перед интегралом, а также знака «−» в показателе эксп��ненты. Но все свойства будут те же, хотя вид некоторых формул может измениться.
Кроме того, существуют разнообразные обобщения данного понятия.
Многомерное преобразование Фурье
Преобразование Фурье функций, заданных на пространстве ℝ^n, определяется формулой:
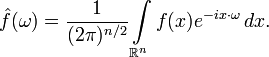
Обратное преобразование в этом случае задается формулой:
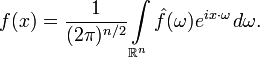
Как и прежде, в разных источниках определения многомерного преобразования Фурье могут отличаться выбором константы перед интегралом.
Дискретное преобразование Фурье
Дискретное преобразование Фурье (в англоязычной литературе DFT, Discrete Fourier Transform) — это одно из преобразований Фурье, широко применяемых в алгоритмах цифровой обработки сигналов (его модификации применяются в сжатии звука в MP3, сжатии изображений в JPEG и др.), а также в других областях, связанных с анализом частот в дискретном (к примеру, оцифрованном аналоговом) сигнале. Дискретное преобразование Фурье требует в качестве входа дискретную функцию. Такие функции часто создаются путём дискретизации (выборки значений из непрерывных функций). Дискретные преобразования Фурье помогают решать дифференциальные уравнения в частных производных и выполнять такие операции, как свёртки. Дискретные преобразования Фурье также активно используются в статистике, при анализе временных рядов. Существуют многомерные дискретные преобразования Фурье.
Формулы дискретных преобразований
Прямое преобразование:
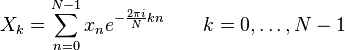
Обратное преобразование:
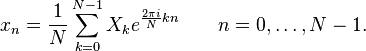
Дискретное преобразование Фурье является линейным преобразованием, которое переводит вектор временных отсчётов в вектор спектральных отсчётов той же длины. Таким образом преобразование может быть реализовано как умножение симметричной квадратной матрицы на вектор:
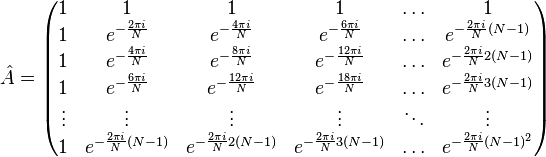
Фурье-преобразования для вычисления свёртки
Одним из замечательных свойств преобразований Фурье является возможность быстрого вычисления корреляции двух функций определённых, либо на действительном аргументе (при использовании классической формулы), либо на конечном кольце (при использовании дискретных преобразований).
И хотя подобные свойства присущи многим линейным преобразованиям, для практического применения, для вычисления операции свёртки, согласно данному нами определению, используется формула
FхG = BFT ( FFT(F)*FFT(G) )
Где
- FFT – операция прямого преобразования Фурье
- BFT – операция обратного преобразования Фурье
Проверить правильность равенства довольно легко – явно подставив в формулы Фурье-преобразований и сократив получившиеся формулы
Фурье-преобразования для вычисления корреляции
Пусть <F,G>(t) равна корреляции получаемой в результате сдвига одного вектора, относительно другого на шаг t
Тогда, как уже показано ранее, выполняется
<F,G>(t) = FхG’(t) = BFT ( FFT(F)*FFT(G’) )
Если используются реализации алгоритма трансформации Фурье через комплексные числа, то такие преобразования обладают ещё одним замечательным свойством:
FFT(G’) = CONJUGATE ( FFT(G) )
Где CONJUGATE ( FFT(G) ) – матрица, составленная из сопряжённых элементов матрицы FFT(G)
Таким образом, получаем
<F,G>(t) = BFT ( FFT(F)*CONJUGATE ( FFT(G) ))
Фурье-преобразования для решения задачи
При использовании формулы для оценки расстояния между изображениями при сдвиге (i,j) относительно друг друга
m(X,Y) (i,j) = <X,Y>(i,j) / ( |X|(i,j) ) * |Y|(i,j) ),
получаем, что
- <X,Y> = XxY’ = BFT ( FFT(X) * CONJUGATE ( FFT(Y) ) )
- |X|^2 = <X,X> = XxX’xE’ = BFT ( FFT(X) * CONJUGATE ( FFT(X) ) * CONJUGATE ( FFT(E) ) ) = BFT ( SQUAREMAGNITUDE( FFT(X) ) * CONJUGATE ( FFT(E) ) )
- |Y|^2 = <Y,Y> = YxY’xE’ = BFT ( FFT(Y) * CONJUGATE ( FFT(Y) ) * CONJUGATE ( FFT(E) ) )
Где
- <X,Y>(i,j) – скалярное произведение двух изображений, получаемых при сдвиге (i,j) относительно друг друга изображений X и Y
- E – изображение размера равному минимальным размерам X и Y, и заполненное единичными значениями (то есть “кадр” в котором сравниваются X и Y)
- |X|(i,j) – норма общей части изображения X при сдвиге (i,j)
- |Y|(i,j) – норма общей части изображения Y при сдвиге (i,j)
- FFT – операция прямого двухмерного дискретного преобразования Фурье
- BFT – операция обратного двухмерного дискретного преобразования Фурье
- CONJUGATE – операция вычисления матрицы из сопряжённых элементов
- SQUAREMAGNITUDE– операция вычисления матрицы квадратов амплитуд элементов
Упрощение формул для решения поставленной задачи
При решении задачи для поиска одного образца, дополнительное нормирование образца является излишним, а также вычисление нормы у общей части может быть заменено на сумму яркостей пикселей в этой общей части или на сумму квадратов яркостей в этой общей части
При использовании формулы для оценки расстояния между изображениями при сдвиге (i,j) относительно друг друга
m(X,Y) (i,j) = <X,Y>(i,j) / |X|^2(i,j),
получаем, что
- <X,Y> = BFT ( FFT(X) * CONJUGATE ( FFT(Y) ) )
- <X,X> = BFT ( SQUAREMAGNITUDE( FFT(X) ) * CONJUGATE ( FFT(E) ) )
Где
- <X,Y>(i,j) – скалярное произведение двух изображений, получаемых при сдвиге (i,j) относительно друг друга изображений X и Y
- E – изображение размера равному минимальным размерам X и Y, и заполненное единичными значениями (то есть “кадр” в котором сравниваются X и Y)
- <X,X>(i,j) – норма (сумма яркостей пикселей) общей части изображения X при сдвиге (i,j)
- FFT – операция прямого двухмерного дискретного преобразования Фурье
- BFT – операция обратного двухмерного дискретного преобразования Фурье
- CONJUGATE – операция вычисления матрицы из сопряжённых элементов
- SQUAREMAGNITUDE– операция вычисления матрицы квадратов амплитуд элементов
Алгоритм поиска фрагмента в полном изображении
- Пусть даны два изображения X и Y – изображение и образец, размеров (N1,N2) и (M1,M2) соответственно и Ni > Mi
- Требуется найти координаты образца Y в полном изображении X и вычислить оц��ночную величину — меру близости.
- Расширить изображение Y до размера (N1,N2), дополнив его нулями
- Сформировать изображение E из единиц размера (M1,M2) и расширить до размера (N1,N2), дополнив его нулями
- Вычислить <X,Y> = BFT ( FFT(X) * CONJUGATE ( FFT(Y) ) )
- Вычислить <X,X> = BFT ( SQUAREMAGNITUDE( FFT(X) ) * CONJUGATE ( FFT(E) ) )
- Вычислить M[i,j] = (f + <X,Y> [i,j])/(f + <X,X> [i,j])
- В матрице M найти элемент с максимальным значением – координаты этого элемента и являются искомой позицией образца в полном изображении, а значение равно оценке меры сравнения.
Примечание:
При использовании дискретного преобразования Фурье, матрица M содержит также элементы от циклического сдвига изображений между собой. Поэтому, если не требуется анализировать циклический сдвиг кадров, то поиск максимального элемента в матрице M нужно ограничить областью (0,0)-(N1-M1, N2-M2).
Примеры реализации
Реализованные алгоритмы являются частью библиотеки с открытым исходным кодом FFTTools. Интернет-адрес: github.com/dprotopopov/FFTTools
Используемое программное обеспечение
- Microsoft Visual Studio 2013 C# — среда и язык программирования
- EmguCV/OpenCV – C++ библиотека структур и алгоритмов для обработки изображений
- FFTWSharp/FFTW – C++ библиотека реализующая алгоритмы быстрого дискретного преобразования Фурье
/// <summary> /// Catch pattern bitmap with the Fastest Fourier Transform /// </summary> /// <returns>Matrix of values</returns> private Matrix<double> Catch(Image<Gray, double> image) { const double f = 1.0; int length = image.Data.Length; int n0 = image.Data.GetLength(0); int n1 = image.Data.GetLength(1); int n2 = image.Data.GetLength(2); Debug.Assert(n2 == 1); // Allocate FFTW structures var input = new fftw_complexarray(length); var output = new fftw_complexarray(length); fftw_plan forward = fftw_plan.dft_3d(n0, n1, n2, input, output, fftw_direction.Forward, fftw_flags.Estimate); fftw_plan backward = fftw_plan.dft_3d(n0, n1, n2, input, output, fftw_direction.Backward, fftw_flags.Estimate); var matrix = new Matrix<double>(n0, n1); double[,,] patternData = _patternImage.Data; double[,,] imageData = image.Data; double[,] data = matrix.Data; var doubles = new double[length]; // Calculate Divisor Copy(patternData, data); Buffer.BlockCopy(data, 0, doubles, 0, length*sizeof (double)); input.SetData(doubles.Select(x => new Complex(x, 0)).ToArray()); forward.Execute(); Complex[] complex = output.GetData_Complex(); Buffer.BlockCopy(imageData, 0, doubles, 0, length*sizeof (double)); input.SetData(doubles.Select(x => new Complex(x, 0)).ToArray()); forward.Execute(); input.SetData(output.GetData_Complex().Zip(complex, (x, y) => x*Complex.Conjugate(y)).ToArray()); backward.Execute(); IEnumerable<double> doubles1 = output.GetData_Complex().Select(x => x.Magnitude); if (_fastMode) { // Fast Result Buffer.BlockCopy(doubles1.ToArray(), 0, data, 0, length*sizeof (double)); return matrix; } // Calculate Divider (aka Power) input.SetData(doubles.Select(x => new Complex(x*x, 0)).ToArray()); forward.Execute(); complex = output.GetData_Complex(); CopyAndReplace(_patternImage.Data, data); Buffer.BlockCopy(data, 0, doubles, 0, length*sizeof (double)); input.SetData(doubles.Select(x => new Complex(x, 0)).ToArray()); forward.Execute(); input.SetData(complex.Zip(output.GetData_Complex(), (x, y) => x*Complex.Conjugate(y)).ToArray()); backward.Execute(); IEnumerable<double> doubles2 = output.GetData_Complex().Select(x => x.Magnitude); // Result Buffer.BlockCopy(doubles1.Zip(doubles2, (x, y) => (f + x*x)/(f + y)).ToArray(), 0, data, 0, length*sizeof (double)); return matrix; }
/// <summary> /// Copy 3D array to 2D array (sizes can be different) /// Flip copied data /// Reduce last dimension /// </summary> /// <param name="input">Input array</param> /// <param name="output">Output array</param> private static void Copy(double[,,] input, double[,] output) { int n0 = output.GetLength(0); int n1 = output.GetLength(1); int m0 = Math.Min(n0, input.GetLength(0)); int m1 = Math.Min(n1, input.GetLength(1)); int m2 = input.GetLength(2); for (int i = 0; i < m0; i++) for (int j = 0; j < m1; j++) output[i, j] = input[i, j, 0]; for (int k = 1; k < m2; k++) for (int i = 0; i < m0; i++) for (int j = 0; j < m1; j++) output[i, j] += input[i, j, k]; } /// <summary> /// Copy 3D array to 2D array (sizes can be different) /// Replace items copied by value /// Flip copied data /// Reduce last dimension /// </summary> /// <param name="input">Input array</param> /// <param name="output">Output array</param> /// <param name="value">Value to replace copied data</param> private static void CopyAndReplace(double[,,] input, double[,] output, double value = 1.0) { int n0 = output.GetLength(0); int n1 = output.GetLength(1); int m0 = Math.Min(n0, input.GetLength(0)); int m1 = Math.Min(n1, input.GetLength(1)); int m2 = input.GetLength(2); for (int i = 0; i < m0; i++) for (int j = 0; j < m1; j++) output[i, j] = value; } /// <summary> /// Find a maximum element in the matrix /// </summary> /// <param name="matrix">Matrix of values</param> /// <param name="x">Index of maximum element</param> /// <param name="y">Index of maximum element</param> /// <param name="value">Value of maximum element</param> public void Max(Matrix<double> matrix, out int x, out int y, out double value) { double[,] data = matrix.Data; int n0 = data.GetLength(0); int n1 = data.GetLength(1); value = data[0, 0]; x = y = 0; for (int i = 0; i < n0; i++) { for (int j = 0; j < n1; j++) { if (data[i, j] < value) continue; value = data[i, j]; x = j; y = i; } } } /// <summary> /// Catch pattern bitmap with the Fastest Fourier Transform /// </summary> /// <returns>Array of values</returns> public Matrix<double> Catch(Bitmap bitmap) { using (var image = new Image<Gray, Byte>(bitmap)) return Catch(image); }
Попался, который кусался

Литература
- А.Л. Дмитриев. Оптические методы обработки информации. Учебное пособие. СПб. СПюГУИТМО 2005. 46 с.
- А.А.Акаев, С.А.Майоров «Оптические методы обработки информации» М.:1988
- Дж.Гудмен «Введение в Фурье-оптику» М.: Мир 1970
