Заметки с MBC Symposium: еще о седловых точках

[Monnoroch]

У меня всегда было ощущение, что с седловыми точками как раз призваны сражаться модернизированные методы оптимизации с моментом и прочими наворотами. На интуитивном уровне кажется, что вторые производные лучше момента только в теории (ну и может на практике только количественно и не очень уж сильно), ведь добавление момента в каком-то смысле делает оптимизационный метод второго порядка: с «ускорением».

решает проблему vanishing gradients и дает тренировать сколь угодно глубокую линейную систему за одинаковое количество градиентных шагов.

Не одинаковое, а ограниченно растущее. Это значит, что в какой-то момент увеличение числа слоев перестает увеличивать время обучения, но вот что это за момент и насколько скоро он наступает — еще вопрос. Теоретический результат хорош, но применим ли он к нелинейным сетям и к глубине сетей принятой в жизни пока не ясно.

[sim0nsays]

Все так, RMSProp, adagrad и прочее — как раз для этого, но не сказать, что они эту задачу всегда решают успешно. Когда шума много, маленький сигнал из правильного направления легко забить :(

Про второе — хм, он по-моему в докладе прямо говорил, что мол indepedent, график показывал —
Или вы прочитали статью и это все обман?

[Monnoroch]

Я прочитал статью и там есть очень другая картинка:


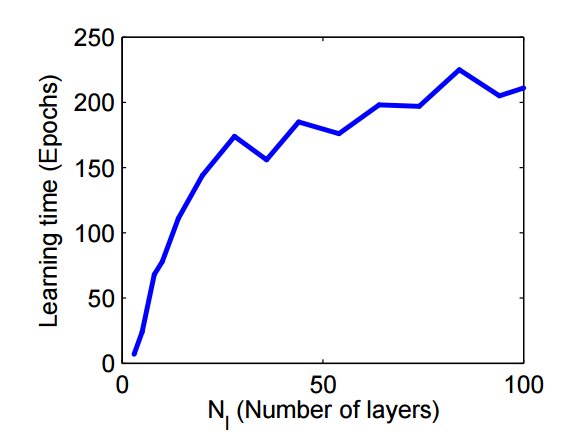
Какая-то из них врет и вот эта мне кажется гораздо более правдоподобной :)

[sim0nsays]

Стоять! Это была статья про их улучшенный метод градиентного спуска, это вообще не про иницализацию. Инициализацию они обсуждают тут — http://arxiv.org/pdf/1312.6120.pdf, и там натурально независимо от глубины (искать по словам orthogonal initialization).

Поправлю пост

[Monnoroch]

А вот и не стоять, моя картинка как раз из правильной статьи про инициализацию.

[sim0nsays]

Ок, но она же вроде из секции до init conditions? Т.е. supposedly они при получении этого графика ее не применяли. А дальше там те же графики, что и на скрине, который я привел выше.

[Monnoroch]

И это тоже не правда, вот часть описания эксперимента на моей картинке:

Networks were initialized with decoupled initial conditions and starting initial mode strength u0 = 0.001…
Thus learning times in deep linear networks that start with decoupled initial conditions are only a finite
amount slower than a shallow network regardless of depth

То есть, они уже тут применяют ключевую идею статьи про decoupled initial conditions. Возможно, дальше они дополнительно сделали что-то еще и получили еще более крутые результаты, как на вашей картинке, но я пока не понял, что же именно.

[sim0nsays]

Прежде всего, спасибо за обсуждение — пришлось таки прочитать статью :)

Насколько я понимаю, этот график из секции про экспериментальное подтверждение тезиса, что с ростом глубины сети время тренировки в количестве эпох выходит на константу. Она у них довольно высокая, потому что они выбрали значение главной моды маленьким, а время схождения от нее зависит квадратично.
В следующей секции они сначала исследуют возможность делать unsupervised pretraining на input set, который мол получает начальные значения с модой близкой к 1, поэтому сходится гораздо быстрее. Про это у них дальше картинка:

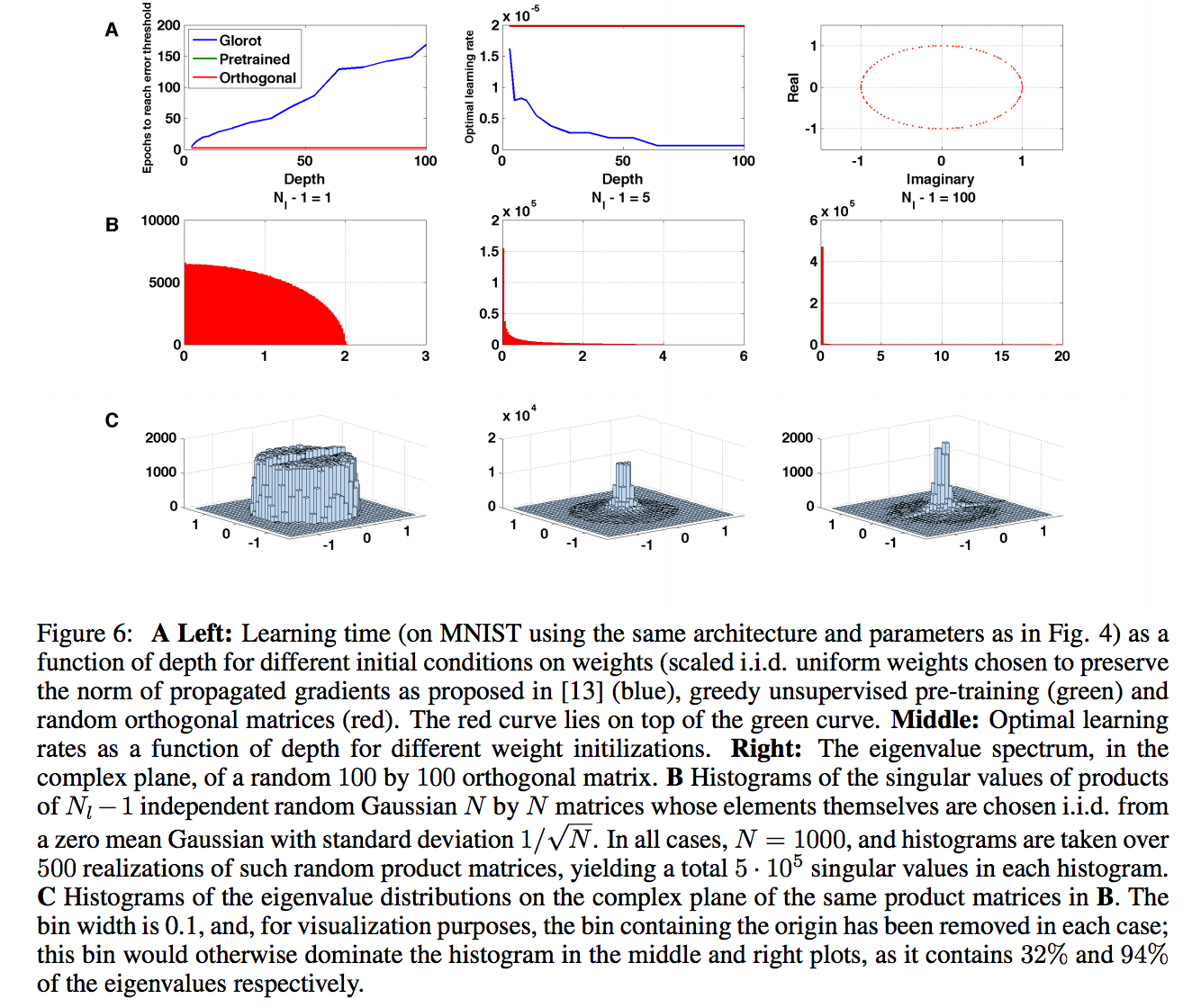
И далее сноска:

(as a technical point: note that learning times under greedy pre-training initialization in Fig. 6A are faster than those obtained in Fig. 4 by explicitly choosing a point on the decoupled submanifold, because there
the initial mode strength was chosen to be small (u = 0.001) whereas greedy pre-training finds a composite
mode strength closer to 1)

Что видимо как раз отвечает на обсуждаемый нами вопрос.

Далее они предлагают вместо дорогой процедуры pretraining использовать тупо ортогональные матрицы для весов (что отличается от depoupled conditions, если я не путаю, потому что decoupled conditions зависят от атупута тоже), и они сходятся тоже с константой скоростью, видимо у них тоже мода хорошая.

[Monnoroch]

Спасибо, я тоже уже вчитался еще раз в детали статьи и пришел к тем же выводам. Однако, мне все равно не верится, что эти результаты обобщатся на произвольные модели. Все-таки, обучить модель любого размера за пару-тройку эпох (судя по графику) — это какая-то фантастика.

[sim0nsays]

О да, я тоже полон сомнений. В случае нелинейных моделей и других датасетов все может легко развалиться. Тем более, попробовать просто, а что-то никто не рапортует об успехах.

[Monnoroch]

Я попробую, как время будет на моих RCGAN-ах, с которыми я сейчас играю и которые реально сложно оптимизировать.

[Monnoroch]

Потому, что вокруг седла во все стороны очень пологое плато и кажется, что все, оптимизация закончилась, когда на самом деле нет.