Введение
В предыдущем посте я постарался описать, как легко можно воспользоваться преимуществом GPU для обработки изображений. Судьба сложилась так, что мне подвернулась возможность попробовать улучшить медианную фильтрацию для GPU. В данном посте я постараюсь рассказать каким образом можно получить еще больше производительности от GPU в обработке изображений, в частности, на примере медианной фильтрации. Сравнивать будем GPU GTX 780 ti с оптимизированным кодом, запущенном на современном процессоре Intel Core i7 Skylake 4.0 GHz с набором векторных регистров AVX2. Достигнутая скорость фильтрации квадратом 3х3 в 51 GPixels/sec для GPU GTX 780Ti и удельная скорость фильтрации квадратом 3х3 в 10.2 GPixels/sec на 1 TFlops для одинарной точности на данное время являются самыми высокими из всех известных в мире.
Для ясности происходящего настоятельно рекомендуется прочитать предыдущий пост, так как данный пост будет пре��ставлять собой советы, рекомендации и подходы к улучшению уже написанной версии. Для напоминания, что мы делаем:
- Для каждой точки исходного изображения берется некоторая окрестность (в нашем случае 3x3 / 5х5).
- Точки данной окрестности сортируются по возрастанию яркости.
- Средняя точка отсортированной окрестности записывается в итоговое изображение.
Медианный фильтр квадратом 3х3
Один из способов оптимизации кода по обработке изображений на GPU — найти и выделить повторные операции и сделать их только один раз внутри одного warp'а. В некоторых случаях потребуется немного изменить алгоритм. Рассматривая фильтрацию, можно заметить, что, загружая квадрат 3х3 вокруг одного пикселя, соседние нити делают одинаковые логические операции и одинаковые загрузки из памяти:
__global__ __launch_bounds__(256, 8) void mFilter_3х3(const int H, const int W, const unsigned char * __restrict in, unsigned char *out) { int idx = threadIdx.x + blockIdx.x * blockDim.x + 1; int idy = threadIdx.y + blockIdx.y * blockDim.y * 4 + 1; unsigned a[9] = { 0, 0, 0, 0, 0, 0, 0, 0, 0 }; if (idx < W - 1) { for (int z3 = 0; z3 < 4; ++z3) { const int shift = 8 * (3 - z3); for (int z2 = 0; z2 < 3; ++z2) for (int z1 = 0; z1 < 3; ++z1) a[3 * z2 + z1] |= in[(idy - 1 + z2) * W + idx - 1 + z1] << shift; // <----- Здесь каждый warp делает лишние // 6 операций загрузки и 12 логических // операций idy += BL_Y; } /* Остальной код далее */ } }
Немного подумав, можно улучшить сортировку, делая одинаковые операции только один раз. Для наглядности я покажу какая сортировка была и какая стала, и в чем выгода от такого подхода.
В предыдущем посте я использовал уже придуманную неполную сортировку Бэтчера для 9ти элементов, которая позволяет найти медиану не используя условные операторы за минимальное количество операций. Представим эту сортировку в виде итераций, на каждой из которых сортируются независимые элементы, но между итерациями присутствуют зависимости. Для каждой итерации выделены пары элементов для сортировки.
Старая сортировка:

Новая сортировка:
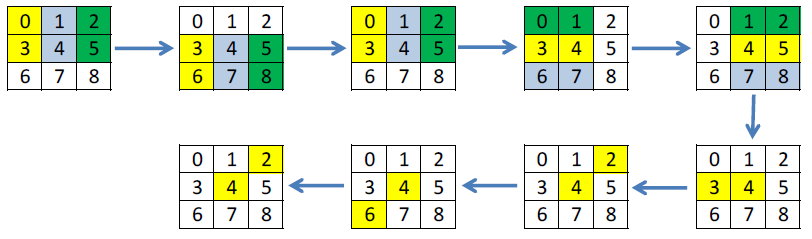
На вид, оба подхода можно сказать одинаковые. Но посмотрим на это с точки зрения оптимизации по количеству операций и возможности использовать вычисленные значения другими нитями. Можно выполнить загрузку и сортировку столбцов только один раз, сделать обмены между нитями и досчитать медиану. Наглядно это будет выглядеть так:

Такому алгоритму соответствует следующее ядро. Для обменов я решил использовать не разделяемую память, а новые операции __shfl, которые позволяют без синхронизации обменяться значениями внутри одного warp'а. Таким образом, удается частично не делать повторные вычисления.
__global__ BOUNDS(BL_X, 2048 / BL_X) void mFilter_3x3(const int H, const int W, const unsigned char * __restrict in, unsigned char *out) { // индекс по Оси Х int idx = threadIdx.x + blockIdx.x * blockDim.x; // смещаемся немного назад, так как в каждом warp'е первая и последняя нить не участвует в итоговом вычислении idx = idx - 2 * (idx / 32); // умножаем на 4, так как мы обрабатываем по 4 точки сразу int idy = threadIdx.y + blockIdx.y * blockDim.y * 4 + 1; unsigned a[9]; unsigned RE[3]; // первая и последняя нить не участвует в итоговом вычислении bool bound = (idxW > 0 && idxW < 31 && idx < W - 1); // считываем и сортируем столбцы RE[0] = in[(idy - 1) * W + idx] | (in[(idy + 0) * W + idx] << 8) | (in[(idy + 1) * W + idx] << 16) | (in[(idy + 2) * W + idx] << 24); RE[1] = in[(idy + 0) * W + idx] | (in[(idy + 1) * W + idx] << 8) | (in[(idy + 2) * W + idx] << 16) | (in[(idy + 3) * W + idx] << 24); RE[2] = in[(idy + 1) * W + idx] | (in[(idy + 2) * W + idx] << 8) | (in[(idy + 3) * W + idx] << 16) | (in[(idy + 4) * W + idx] << 24); Sort(RE[0], RE[1]); Sort(RE[1], RE[2]); Sort(RE[0], RE[1]); // делаем обмены a[0] = __shfl_down(RE[0], 1); a[1] = RE[0]; a[2] = __shfl_up(RE[0], 1); a[3] = __shfl_down(RE[1], 1); a[4] = RE[1]; a[5] = __shfl_up(RE[1], 1); a[6] = __shfl_down(RE[2], 1); a[7] = RE[2]; a[8] = __shfl_up(RE[2], 1); // ищем максимум a[2] = __vmaxu4(a[0], __vmaxu4(a[1], a[2])); // ищем медиану Sort(a[3], a[4]); a[4] = __vmaxu4(__vminu4(a[4], a[5]), a[3]); // ищем минимум a[6] = __vminu4(a[6], __vminu4(a[7], a[8])); // ищем финально медиану Sort(a[2], a[4]); a[4] = __vmaxu4(__vminu4(a[4], a[6]), a[2]); // записываем результат, если не вышли за границу картинки if (idy + 0 < H - 1 && bound) out[(idy) * W + idx] = a[4] & 255; if (idy + 1 < H - 1 && bound) out[(idy + 1) * W + idx] = (a[4] >> 8) & 255; if (idy + 2 < H - 1 && bound) out[(idy + 2) * W + idx] = (a[4] >> 16) & 255; if (idy + 3 < H - 1 && bound) out[(idy + 3) * W + idx] = (a[4] >> 24) & 255; }
Вторая оптимизация связана с тем, что каждая нить может обрабатывать не 4 точки сразу, а, например, 2 набора по 4 точки или N наборов по 4 точки. Это нужно для того, чтобы максимально загрузить работу устройства, так как именно для фильтра 3х3 одного набора по 4 точки недостаточно.
Третья оптимизация, которую еще можно сделать — выполнить подстановку значений ширины и высоты картинки. На это есть несколько аргументов:
- Обычно размеры картинок имеют фиксированные значения, например, популярные Full HD, Ultra HD, 720p. Можно просто иметь набор предкомпилированных ядер. Данная оптимизация дает порядка 10-15% к производительности.
- С версии Cuda Toolkit 7.5 появилась возможность выполнять динамическую компиляцию, которая позволяет выполнить подстановку значений во время выполнения.
Полностью оптимизированный код будет выглядеть так. Варьируя количество точек, можно получить максимальную производительность. В моем случае максимальная производительность была достигнута при numP_char = 3, то есть три набора по 4 точки или 12 точек на одну нить.
__global__ BOUNDS(BL_X, 2048 / BL_X) void mFilter_3x3(const unsigned char * __restrict in, unsigned char *out) { int idx = threadIdx.x + blockIdx.x * blockDim.x; idx = idx - 2 * (idx / 32); int idxW = threadIdx.x % 32; int idy = threadIdx.y + blockIdx.y * blockDim.y * (4 * numP_char) + 1; unsigned a[numP_char][9]; unsigned RE[numP_char][3]; bool bound = (idxW > 0 && idxW < 31 && idx < W - 1); #pragma unroll for (int z = 0; z < numP_char; ++z) { RE[z][0] = in[(idy - 1 + z * 4) * W + idx] | (in[(idy - 1 + 1 + z * 4) * W + idx] << 8) | (in[(idy - 1 + 2 + z * 4) * W + idx] << 16) | (in[(idy - 1 + 3 + z * 4) * W + idx] << 24); RE[z][1] = in[(idy + z * 4) * W + idx] | (in[(idy + 1 + z * 4) * W + idx] << 8) | (in[(idy + 2 + z * 4) * W + idx] << 16) | (in[(idy + 3 + z * 4) * W + idx] << 24); RE[z][2] = in[(idy + 1 + z * 4) * W + idx] | (in[(idy + 1 + 1 + z * 4) * W + idx] << 8) | (in[(idy + 1 + 2 + z * 4) * W + idx] << 16) | (in[(idy + 1 + 3 + z * 4) * W + idx] << 24); Sort(RE[z][0], RE[z][1]); Sort(RE[z][1], RE[z][2]); Sort(RE[z][0], RE[z][1]); a[z][0] = __shfl_down(RE[z][0], 1); a[z][1] = RE[z][0]; a[z][2] = __shfl_up(RE[z][0], 1); a[z][3] = __shfl_down(RE[z][1], 1); a[z][4] = RE[z][1]; a[z][5] = __shfl_up(RE[z][1], 1); a[z][6] = __shfl_down(RE[z][2], 1); a[z][7] = RE[z][2]; a[z][8] = __shfl_up(RE[z][2], 1); a[z][2] = __vmaxu4(a[z][0], __vmaxu4(a[z][1], a[z][2])); Sort(a[z][3], a[z][4]); a[z][4] = __vmaxu4(__vminu4(a[z][4], a[z][5]), a[z][3]); a[z][6] = __vminu4(a[z][6], __vminu4(a[z][7], a[z][8])); Sort(a[z][2], a[z][4]); a[z][4] = __vmaxu4(__vminu4(a[z][4], a[z][6]), a[z][2]); } #pragma unroll for (int z = 0; z < numP_char; ++z) { if (idy + z * 4 < H - 1 && bound) out[(idy + z * 4) * W + idx] = a[z][4] & 255; if (idy + 1 + z * 4 < H - 1 && bound) out[(idy + 1 + z * 4) * W + idx] = (a[z][4] >> 8) & 255; if (idy + 2 + z * 4 < H - 1 && bound) out[(idy + 2 + z * 4) * W + idx] = (a[z][4] >> 16) & 255; if (idy + 3 + z * 4 < H - 1 && bound) out[(idy + 3 + z * 4) * W + idx] = (a[z][4] >> 24) & 255; } }
Медианный фильтр квадратом 5х5
К сожалению, придумать какую то другую сортировку для квадрата 5х5 мне так и не удалось. Единственное, на чем можно сэкономить — на загрузке и объединении 4х точек в unsigned int. Привод��ть еще более длинный код я не вижу смысла, так как все преобразования можно проделать по аналогии с квадратом 3х3.
В данной статье описаны некоторые идеи по совмещению операций для двух квадратов с наложением в 20 элементов. Но предложенный авторами метод forgetful selection sort делает все равно больше операций, чем неполная сеть сортировки Бэтчера для 25 элементов, даже при объединении двух рядом расположенных квадратов 5х5.
Производительность
Наконец, приведу некоторые цифры, которые я смог получить на протяжении всего процесса оптимизации.
| Время выполнения, ms | Ускорение | |||||
|---|---|---|---|---|---|---|
| Скалярный ЦПУ | AVX2 ЦПУ | GPU | Скалярный / GPU | AVX2 / GPU | ||
| 3x3 1920x1080 | 22.9 | 0.255 | 0.044 (47.1 GP/s) | 520 | 5.8 | |
| 3x3 4096x2160 | 97.9 | 1.33 | 0.172 (51.4 GP/s) | 569 | 7.73 | |
| 5x5 1920x1080 | 134.3 | 1.47 | 0.260 (7.9 GP/s) | 516 | 5.6 | |
| 5x5 4096x2160 | 569.2 | 6.69 | 1.000 (8.8 GP/s) | 569 | 6.69 | |
Заключение
В заключении хочется отметить, что среди всех найденных статей и реализаций медианной фильтрации для GPU, интерес представляет уже упомянутая статья "Fine-tuned high-speed implementation of a GPU-based median filter", опубликованная в 2013 году. В данной статье авторы предложили совершенно другой подход к сортировке, а именно — метод forgetful selection. Суть данного метода заключается в том, что мы берем roundUp(N / 2) + 1 элементов, проходим слева направо и обратно, получая тем самым минимальный и максимальный элементы по краям. Далее забываем эти элементы, добавляем один из оставшихся элементов в конец и повторяем процесс. Когда добавлять уже будет нечего, мы получим массив из 3х элементов, из которых медиану выбрать будет уже просто. Один из плюсов данного подхода — уменьшенное количество используемых регистров, по сравнению с известными сортировками.
В статье указано, что авторы получили результат в 1.8 GPixels / sec на Tesla C2050. Мощность данной карты в одинарной точности оценивается в 1 TFlops. Мощность участвующей в тестировании 780Ti оценивается в 5 TFlops. Тем самым, удельная скорость вычислений на 1 TFlops предложенного мной алгоритма примерно в 5.5 раз больше для квадрата 3х3 и в 2 раза больше для квадрата 5х5, чем у предложенного авторами статьи. Данное сравнение является не совсем корректным, но более приближенным к истине. Также в данной статье было упомянуто, что на тот момент их реализация была самой быстрой из всех известных.
Достигнутое ускорение по сравнению с AVX2 версией составило в среднем в 6 раз. Если использовать новые карты на базе архитектуры Pascal, данное ускорение может увеличиться как минимум в 2 раза, что составит примерно 100 GPixels / sec.
