«Правда, чистая правда и статистика» или «15 распределений вероятности на все случаи жизни»

[GeMir]

Неплохо бы статью перед публикацией показать корректору, который почистит текст от остатков «(3/10) х (2/9)» и «Г(x)» (раз уж в большинстве случаев используется красивый TeX). Нумерация формул кажется лишней, а сама статья скорее похожа на цитату из скрипта лекции по вероятностному исчислению. Справочников по теме предостаточно и как студенты, так и «зрелые специалисты», думается мне, первым делом обратятся к ним, а не к поиску по Хабру.

[JamaGava]

Спасибо за комментарий. По поводу формул — согласен, буду дорабатывать.
А что касается тематики и нумерации формул: эта статья «база» для дальнейших более IT-шных статей по анализу данных (чтобы ставить ссылки на конкретные формулы, собранные вместе).

[kxx]

И есть небольшая неточность: биномиальный коэффициент записывается обычно либо как , либо как , но не как .

[JamaGava]

Это действительно ляп с моей стороны… Спасибо.
Уже исправлено.

[parpalak]

Картинки, кстати, тоже можно сделать красивыми:



Вот исходник:

\begin{tikzpicture}[mark=*,mark size=1,only marks]
\begin{axis}[
    yticklabel style={/pgf/number format/fixed},
    ymax=0.25,
    width=10cm,
    declare function={binom(\k, \n, \p)=(\p^(\k))*((1-\p)^(\n-\k))*factorial(\n)/(factorial(\n-\k)*factorial(\k));}
]
\addlegendimage{blue}
\addlegendimage{green}
\addlegendimage{red}
\foreach \n/\p/\c in {20/0.5/blue, 20/0.7/green, 40/0.5/red} {
    \foreach \k in {0,...,\n} {
        \edef\temp{\noexpand
            \addplot[\c] coordinates {(\k,{binom(\k, \n, \p)})};
        }\temp
    }
    \edef\temp{\noexpand
        \addlegendentry{$p=\p, n=\n$}
    }\temp
}
\end{axis}
\end{tikzpicture}

[tomzarubin]

Непонятно почему вы считаете свой график лучше представленных выше. Точки тут неуместны— чтобы понять о чём график(а потом и форму распределения), надо напрячься.

[parpalak]

Согласен, конечно. Мы тут обсуждали оформление, а не содержание.

В тексте была откуда-то скопированная png-картинка. Моя svg-картинка сделана в латехе с пакетом tikz. Способ не без проблем: человеку без опыта тяжело сразу готовить такие картинки. Зато исходник можно править на лету, не перерисовывая картинку. Я вот за 5 минут поменял точки на столбцы, и диаграмма стала понятнее:

[tomzarubin]

Постойте, так про оформление и речь. Пример выше, конечно, чище и понятней.

[JamaGava]

Такие диаграммы красивее. Я взял материал со страниц википедии (в тексте приведены ссылки). Если для кого-нибудь действительно совсем несложно переделать графики — Вы можете улучшить Вики.
Сам бы занялся, но не владею технологией построения настолько красивых диаграмм :)
(Хотя, уже захотелось освоить)

[parpalak]

Переделать — не сложно, но и не просто :)

Хотите освоить — посмотрите введение к официальной документации tikz. В нем последовательным усложнением строятся полноценные примеры графиков и диагамм. Это хорошая отправная точка.

[JamaGava]

Спасибо

[tomzarubin]

Я не в претензии)
Кстати, в R есть прекрасные библиотеки. Тот же «классический уже» ggplot2 или seaborn + несколько библиотек интерактивных графиков.
Ну и R, по ощущениям, очень прекрасен для статистики и EDA. Самое главное— побороть непонимание синтаксиса самого R.

[temas]

Интересно, но ожидал больше примеров. (В дискретных распределениях примеры были)

[JamaGava]

Большой пример скоро будет в отдельной статье

[Lelushak]

Зачем захламлять теги отдельным названием каждого распределения? У них другое предназначение.

[ratatosk]

Вот очень хорошая вводная статья про виды распределений: Common Probability Distributions: The Data Scientist’s Crib Sheet.

[JamaGava]

Название действительно провокационное, для привлечения внимания. В самой статье я пишу, что предложенные распределения используются в «наиболее часто встречающихся задачах».

Что касается «дз» это тизер готовящейся к публикации работы. Идея такова: мы не можем знать всё обо всех стратегиях, но может поступить по аналогии с тем, как строятся другие стат.тесты, а именно, построить распределение профитфактора для системы, торгующей случайно. Тогда значение профитфактора реальной системы должно быть таковым, чтобы случайное достижения такого значения являлось маловероятным.

[smxfem]

Название статьи провокационное. Получается, что сингулярные распределения — бесполезная альтернатива и создание этих распределений не продиктовано непригодностью описанных тут распределений к некоторым задачам — «случаям жизни»?

Домашнее задание смахивает на задачку с подвохом. Требуется смоделировать множество биржевых систем (тут требуются знания предметной области на уровне бога) и напрямую получить распределения аналитически или откуда-то взять статистику по биржевым системам, подобрать для нескольких дающих надежду распределений оптимальные параметры (оптимизационная задача) и выбрать среди полученных конкретных распределений наиболее точные?

[ShashkovS]

Я просто оставлю это здесь :)


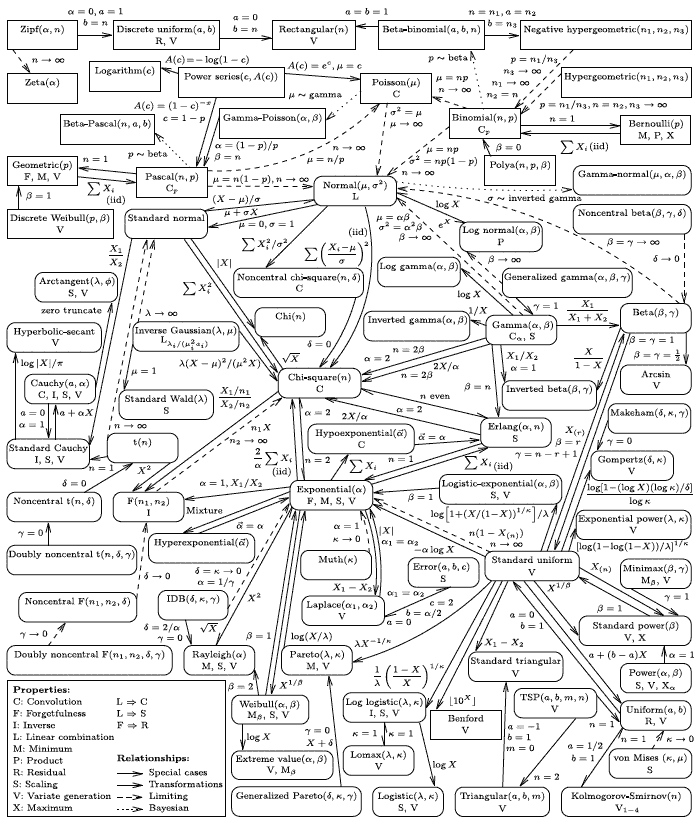
Ну, и с подробностями: http://www.math.wm.edu/~leemis/chart/UDR/UDR.html

[JamaGava]

Вот это действительно: «Вау!» :)
Спасибо!

[JamaGava]

У меня вообще подозрение, что почти все непрерывные распределения должны укладываться в форму , где и — полиномы. Либо являться подстановкой функции (например, нецелой степени либо логарифма) от вместо аргумента в эту формулу.

Кто-нибудь встречал подобные обобщение?

[smxfem]

Есть обобщенное нормальное и обобщенное гиперболическое распределения, которые содержат многие распределения. Но обобщенный вид затрудняет оценку параметров (не критично), а полу-гуманитарные критерии применимости распределений к реальным задачам слабо распространены на такие виды. Попробуйте убедить, предположим, медиков, что какое-то обобщенное распределение лучше подходит для описания некоторой случайной величины, когда 100 лет уже её описывают в обширных исследованиях, которые считаются фундаментальными, более простым частным распределением. Хотя, если, после оценки, вклад всех параметров в распределение будет существенным, то никто не отвертится и придется принять обобщение.
Знакомый психолог публиковала в зарубежном журнале статью, где математических претензий не было, а отфутболивали именно из-за отсутствия обоснования применимости использованных распределений, пока не были найдены необходимые подтверждающие ссылки.

[kxx]

Граф впечатляет. Даже не подозревал о некоторых распределениях.

[Leo5700]

Ближайшие полчаса путешествую по графу )

[JamaGava]

Студентам буду на зачёт задание давать: воспроизвести граф по памяти :)

[nickolaym]

Для плотности f(x) и y=g(x), — формула плотности fy(y) справедлива, только если g^-1(y) однозначна. То есть, g(x) биективна. А дифференцируемость g(x) не только недостаточное, но и необязательное условие: легко придумать кучу примеров как с разрывными отображениями
— например, пила вдоль линии y = int(x)-frac(x)
так и дифференцируемые отображения, для которых обратные не дифференцируемы
— например, с седловой точкой, y = x³ (при том, что оно биективно)

[JamaGava]

Согласен с Вашим, замечанием: дифференцируемой должна быть обратная к g(x) (опечатка).

[AndreyIvanoff]

Вот интересное оформление справки по теме.

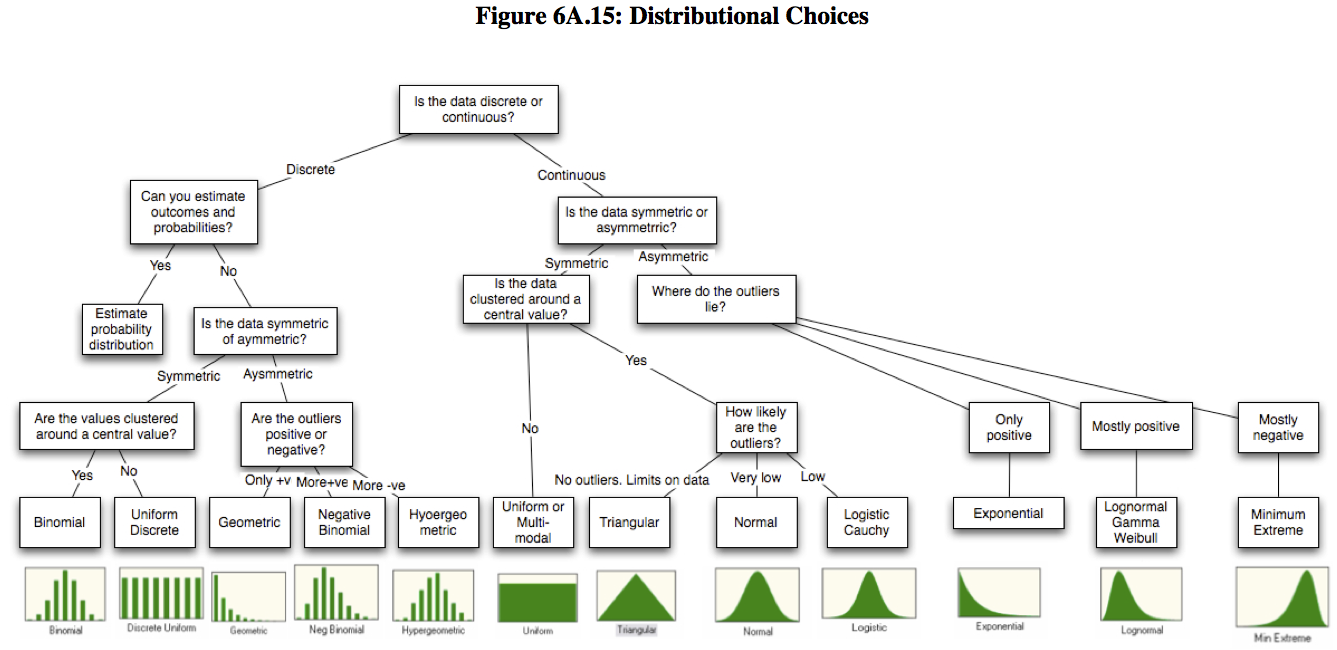
Откуда взял себе, к сожалению, не помню.

[JamaGava]

Действительно красиво сделано.
И информативно.