Комментарии 74
К статье стоит добавить, что не умея пользоваться методами оптимизации, иначе как черным ящиком, практически не возможно повторить эксперименты с тренировкой таких могучих современных сетей, как VGG, ResNet, Inception, etc. с нуля, да и при умении пользоваться тоже приходится с бубном плясать, чтобы получить статейные циферки точности.
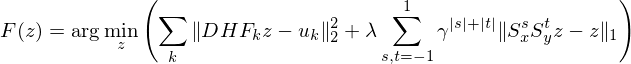
А ведь он вообще идеальный: не имеет локальных минимумов, но Нестеров, например, сходится на порядок быстрее, чем обычный субградиент.
Здесь, правда, всё сводится к опыту: смотрим на график, показывающий поведение ошибки и крутим параметры метода. Наилучшие результаты достигаются при динамически изменяющимся коэффициенте перед шагом градиента (learning rate).
Это, конечно, поспособствовало бы прорыву в AI, но есть гораздо более важные вещи.
Learning to learn by gradient descent by gradient descent (NIPS 2016)
Учат оптимизатор как нейросеть
Где-то с полгода назад видел я статью, где люди сказали «а давайте используем еще одну нейросеть, чтобы выбирать размеры шагов sgd». Вроде показывают, что если обучить всю такую мега систему end-to-end, как сейчас модно, то работает неплохо, но жутко вычислительно неэффективно. Было бы любопытно посмотреть, как та сеть себя поведет на разных ваших примерах, особенно том, где все сфейлили, кроме Adam-а.
Я бы хотел добавить, что дополнительная мотивация увеличивать веса в направлении маленького градиента — это чтобы лучше вылезать из седловых точек, в которых практически всегда застревает отпимизация (настоящий локальный минимум встретить в таком многомерном пространстве — очень маловероятно)
Вот наш кумир Andrej Karpathy в CS231 поясняет - http://cs231n.github.io/neural-networks-3/#ada
а что там ещё помимо DL?
Но если автор этой статьи подтянется глядишь станет на одного больше.
>> «Сорян, сайт временно на реконструкции»
А на сайте кроме формы регистрации в чатике ничего и нет, и по большому счёту и не нужно. Так что он весто останется на реконструкции. :)))
конечно нет, самое большое русскоговорящее это одс, сейчас там 2.5к людей
По соотношению сигнала к шуму ODS сильно проигрывает кружочкам.
Всё таки древовидный форум намного лучше линейного IRC-style чатика.
«When social communities grow past a certain point (Dunbar’s Number?), they start to suck. Be they sororities or IRC channels, there’s a point where they get big enough that nobody knows everybody anymore. The community becomes overwhelmed with noise from various small cliques and floods of obnoxious people and the signal-to-noise ratio eventually drops to near-zero — no signal, just noise. This has happened to every channel I’ve been on that started small and slowly got big.»
И про плоский формат форума: http://inmotion.live/notes/forums-types/
«Плоский формат — Минусы:
— Ответ на вопрос может быть отделен многими страницами флейма.
— Не всегда легко понять, кто кому и на что отвечает.
— Уход разговора «в сторону» и, наоборот, возвращение к основному топику невозможно отследить, не прогрузив всю нить целиком (или несколько страниц).
— Нить – всегда «кот в мешке», на прогрузку и чтение неинтересных дискуссий уходит слишком много времени.»
Добавлю ещё такой нюанс IRC-style формата: если никто не ответил на вопрос хорошо в течение нескольких следующих сообщений, то никто его обсуждать больше не будет. А значит, этот стиль не для сложных вопросов, к которым можно возвращаться через дни или недели.
Содержательных дискуссий (больше чем на 3 фразы) по DL на ODS я за 3 недели не увидел, зато сообщений не по теме и разнообразных смайликов-реакций — сколько угодно.
Может там сейчас не самая "жара", но активных юзеров там не больше 50 (и даже эта оценка завышена) и большинство обсуждений — это small talks на около-ML тематику. В то время как в кружочках при чуть меньшей аудитории (думаю, что там примерно 10-15 боле-мене активных юзеров) концентрация полезных обсуждений выше.
Ну и как правильно пишет buriy, полезные сообщения там легко теряются в потоке отвлеченных разговоров.
Но как тематический чат, да, намного лучше полудохлых telegram-чатов на схожую тематику)
Я как активно состоящий и там, и там, считаю, что тусовки сложились разные и формат обсуждений тоже.
Надо кросс-опылять хорошим контентом!
P.S. С Новым годом!
Nesterov более подвержен застреванию в локальном минимуме, чем SGD.
С чего бы? Действительно, сходимость всех эти оптимизаторов к глобальному минимуму (включая SGD) доказана только в случае выпуклых функций. Но у ванильного SGD вообще нет никаких методов преодолевания «бугров» на пути, на то он и ванильный. Как по мне, так он больше всех подвержен застреванию в локальных минимумах.
А разве кто-то вообще учит сетки, считая градиент ошибки сразу по всей выборке? Вроде бы стандарт де факто — это тренировка на минибатчах.
А разве кто-то вообще учит сетки, считая градиент ошибки сразу по всей выборке?
Вообще-то, да. Например, все квазиньютоновские методы оптимизации. Либа netlab для octave/matlab вообще не умеет минибатчи.
Эта статья — про минимизацию функции. Алгоритм Нестерова — про то же. А когда мы обучаем сеть, то на каждом шаге функция разная. Очень разная. Градиентный спуск в этих условиях, очевидно, сходится (в гугле это доказали математически недавно). Квазиньютоновские методы в этих условиях, очевидно, не сходятся, так как оценивают гессианскую матрицу по значениям градиента в соседних точках, используя BFGS. Если они посчитаны на разных батчах, в гессианской матрице будет мусор.
С алгоритмом Нестерова не все так однозначно. В scikit и caffe он идёт опцией, а не по умолчанию.
На самом деле условие конвексности всей адаптивной поверхности чрезвычайно избыточное. Стоит говорить лишь о достаточной простоте поверхности если она ведёт себя как конвексная на участке, достижимом из текущей точки за несколько (не слишком много) циклов обучения. Это очень важное уточнение, потому что достижимая область для алгоритмов первого порядка, как правило, непосредственно ограничивается скоростью обучения. Уменьшив скорость в 1000 раз вы с удивлением обнаружите, что поверхность, которую изучает ваш алгоритм достаточно простая. Но это не такое важное уточнение.
SGD с моментом (я раньше встречал только такое название Нестерова в неспецифической литературе) действительно подвержен зависанию в локальных минимумах больше чем SGD, но вопрос в том, на сколько более подвержен?
В первом приближении можно сказать, что способность SGD покидать локальные минимумы связана с размерами бросков, которые испытывают веса после каждого изменения, грубо говоря броски должны быть сопоставимы с размерами минимума чтобы алгоритм имел шанс случайно его покинуть. SGD с моментом тоже имеет такие броски, если вдуматься они меньше ровно во столько раз, какое у вас окно округления. Если окно округления 100, то есть параметр 0.99 то броски будут в сто раз меньше. То есть SGD с моментом с скоростью 0.1 будет по способности выходить из локальных минимумов будет аналогичен обычному SGD со скоростью 0.001
Однако реальная функция по которой мы ищем минимум, как правило имеет как участки достаточно простые, так и участки испещрённые локальными минимумами. На простых участках SGD with M от обычного SGD почти не отличается при равной скорости.
Вот и получается, что если вы заранее не знаете рельефа вашей функции или подозреваете, что он может содержать как относительно ровные так и очень зубастые участки, а вы не планируете поправлять параметры вручную очень внимательно следя за сетью, то лучше иметь не SGD v=0.001, а SGD+M v=0.1
Прошу прощения за очень неканонические обозначения.
> Рабочие оптимизаторы второго порядка существуют, но пока что давайте сконцентрируемся на том, что мы можем достигнуть, не рассматривая вторые производные.
Немного позанудствую, Алгоритм Левенберга-Марквардта это все же не совсем метод второго порядка, и он использует первые производные (но не совсем производные от ф-ии ошибки) чтобы аппроксимировать матрицу вторых производных.
Алгоритм Левенберга-Марквардта мне не хватило терпения разобрать по косточкам, но на сколько я успел понять он тоже основан на нектором такого же рода упрощении.
Но что гораздо более важно. все алгоритмы второго порядка намертво застревают в локальных минимумах если к ним не применять жестокое обращение. А применять глубокое обучение обычно имеет смысл только в тех задачах, где этих локальных минимумов милиарды миллионов. В случаях, когда это не так — обычные алгоритмы, гораздо менее капризные чем нейросети дают результат ничуть не хуже.
меня больше удивляет, что такие методы работают хоть как-то вообще. Она капец какая не диагональная, и непростая.
Меня тоже =)
Но ведь если наша аппроксимированная матрица позволяет нам достаточно быстро спускаться, так ли важно точная ли она? Тем более (если я не ошибаюсь), реальная матрица может быть не положительно определенной, и тогда мы не сможем уменьшить ошибку.
И когда я сталкиваюсь с фразами «а давайте, примем для простоты, что она диагональная» и тому подобным меня больше удивляет, что такие методы работают хоть как-то вообще. Она капец какая не диагональная, и непростая.
Всё же лучше, чем считать, что эта же матрица вообще скалярная как в случае простых методов первого порядка.
Но что гораздо более важно. все алгоритмы второго порядка намертво застревают в локальных минимумах если к ним не применять жестокое обращение
А Вы чего хотели? Нахождение глобального минимума невыпуклой задачи – NP сложная задача, никакой надежды на это нет. Радоваться надо тому, что методы второго порядка добираются до локальных минимумов.
А применять глубокое обучение обычно имеет смысл только в тех задачах, где этих локальных минимумов милиарды миллионов
Локальные минимумы есть артифакт модели и функции потерь, непонятно, о каких локальных минимумах Вы говорите, не задав сперва оптимизируемую поверхность.
Локальные минимумы есть артифакт модели и функции потерь, непонятно, о каких локальных минимумах Вы говорите, не задав сперва оптимизируемую поверхность.
Множество локальных минимумов может быть свойством входных данных изучаемой задачи, а не искомой поверхности и метрики которую мы оптимизируем. Приведу простейший пример, с которым когда-то встретился — на входе у вас два действительных числа — координаты, на выходе действительное число — рельеф очень простой функции. В задача почти нет локальных минимумов, сеть учится «в лёт» на нескольких нейронах:
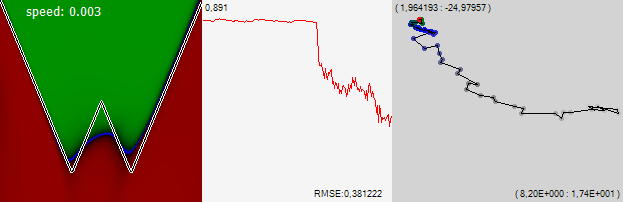
Потом берём ту же самую функцию, но входные денные — 16 бинарных признаков. Первые 8 — битовое разложение первой координаты, вторые 8 то же самое для второй. Аналитически задачка решается слоем из двух нейронов, первый из которых композитит первые 8 бинарных признаков, а второй вторые 8 после чего задача свелась к предыдущей. Но это если логически подумать. А если просто предложить задачу сети, то для неё эта задача имеет чудовищно сложный рельеф с множеством локальных минимумов. И способность быстро найти первый из них даёт угрюмый результат:
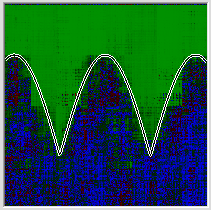
И это при том, что конечная задача и метрика точно такие же. Я не проверял лично, но я почти уверен, что любая задача, входные данные которой будут обладать высокой дискретностью, например текстовой анализ, если на вход подавать не приведённые бинарные признаки слов, будет обладать теми же свойствами, вне зависимости от того какую оптимизируемую поверхность вы зададите, то есть какой вывод будете ожидать от сети.
Конечно можно сказать, что это артефакт модели и если вместо буквально слов подавать на вход их ворд2векнутое представление минимумов будет меньше, но это уже привлечение априорной информации о данных, то есть по сути переформулировка задачи.
Всё же лучше, чем считать, что эта же матрица вообще скалярная как в случае простых методов первого порядка.А вот вопрос лучше ли. Я пока пробовал сравнивать SGD с методами более или менее второго порядка только на узком круге задач, но уже пришёл к мысли, что способность миновать ближайшие локальные минимумы может быть важнее чем способность их быстро найти по крайней мере для задач некоторой сложности. Если поверхность как на иллюстрациях в статье, тогда да, хорошо найти побыстрее какой-нибудь минимум. Но, если вспомнить, что настоящих локальных минимумов в задачах такой размерности почти не бывает, то то что нам касается локальным минимумом на самом деле седловина — один из коридоров лабиринта. Например такого:

И вот теперь вопрос, много ли мне счастья от того что мой алгоритм очень быстро найдёт середину ближайшего от Маши прохода? В такой задаче успех сводится или к умению бодро бегать вдоль туннелей, или скакать через стены.
Конечно открытым остаётся вопрос каков на самом деле рельеф в конкретной задаче. В некоторых самых простых задачах, которые я попробовал результат фактически не зависил от момента, и это свидетельствует, что в них рельеф очень гладкий. Но есть способ проследить за рельефом буквально. Я его в своей статье описывал — присваиваем каждому синапсу произвольный двумерный единичный вектор, и суммируем их все помноженные на веса синапсов. Получается почти произвольная проекция пространства в котором ищет сеть на двумерное пространство, где текущее состояние сети это одна точка. Следя за траекторией этой точки можно предполагать свойства поверхности, по которой она катается в поисках минимума. Я сделал соответствующее видео:
Из которого видно, что даже такая простейшая задача даёт рельеф скорее напоминающий совокупность ямок и соединяющих их туннелей, чем простые поверхности. То есть уже ближе к лабиринту из Маши и Медведей. А та же визуализация для более сложных задач показывает, что там местность ещё гораздо более пересечённая.
И к чему это полотно текста? Во втором примере Вы специфицировали модель, для которой нашли локальные минимумы. Потрудились бы, что ли, доказать, что нельзя моделью с выпуклой поверхностью задачу решить.
Я не проверял лично, но я почти уверен
Вера – это про религию, а мы здесь науку / инженерию обсуждаем.
Вера – это про религию, а мы здесь науку / инженерию обсуждаем.
И если уж на то пошло — большое заблуждение считать что эта область является инженерией. Это гораздо ближе к области блуждающего поиска и описания случайно найденного. Здесь чаще всего не доказывают, а находят и убеждают в применимости. Сколько из 10 последних применённых вами методов имели формально доказанную эфективность?
Если сравнивать DL с наукой, то это скорее география, чем математика.
Жаль
Краткость – сестра таланта. Чем длиннее ваше описание, тем меньше шанс, что Вам удастся донести свою идею до собеседника. Более того, пространные рассуждения плохи ещё и тем, что если собеседник не согласен с одним из ранних тезисов, вся дальнейшая цепь импликаций бессмысленна.
Не имеет значения, география это или математика. Важно лишь то, что это воспроизводимые наблюдения, а Ваше утверждения основываются на частных примерах и "почти уверенности". Как если бы путник, случайно блуждающий в пустыне, говорил о том, что снега не существует.
В рассуждениях про локальные минимумы Вы противоречите себе:
способность миновать ближайшие локальные минимумы может быть важнее чем способность их быстро найти [...] настоящих локальных минимумов в задачах такой размерности почти не бывает, то то что нам касается локальным минимумом на самом деле седловина
Так если локальных минимумов почти нет, зачем же их избегать?
В рассуждениях про локальные минимумы Вы противоречите себе:
Так если локальных минимумов почти нет, зачем же их избегать?
Ну вообще-то это не я говорю а Карпаты и иже с ними. https://habrahabr.ru/post/318970/#comment_9996508 Там это подробно разобрано, что когда люди говорят «локальный минимум» в применении к нейросетям они обычно сталкиваются с седловыми точками — в виде длинных узких тоннелей, в которых обучение вязнет. Если бы вы потрудились прочитать эту портянку, то узнали бы что я вам предложил простой способ как воспроизвести всё мои наблюдения на любой вашей сети наглядно, причём в две питоньи строки, и ещё много чего, что не имеет смысла тут повторять, потому что всё это уже написано один раз, но вам не понравилась какой-то из из тезисов.
Я не сразу понял, что я должен убеждать и очень умело формулировать мой текст чтобы вы стали интересоваться сутью написанного. Но мне сказали, что вы вдумчивый интересный комментатор на ods, вот я и полез, как дурак, тратить своё и ваше время.
Жаль.
Ну вообще-то это не я говорю а Карпаты и иже с ними
Это где он такое говорит, можно конкретную ссылку? Хочется избегать седловых точек, да, а вот локальные минимумы нас вполне устраивают (тем более, что их слишком мало, чтобы ими пренебрегать)
когда люди говорят «локальный минимум» в применении к нейросетям они обычно сталкиваются с седловыми точками
Не надо подменять понятия, седловые точки и локальные минимумы – разные вещи.
Чтобы я не пытался вам ничего объяснять? Так этого результата вы добились своим первым комментарием. Или я был слишком глуп чтобы начать с вами чем-то поделиться. Или вы слишком умны чтобы мочь воспринимать эти, в общем-то, очень простые вещи если они не написаны наукообразно. Но даже если бы это было не так — попытки придираться к словам не обогатили бы знаниями ни одного из нас.
1) Выбор для момента чисел порядка 0.9 исторически сложился, но не имеет под собой рациональных оснований. Если ты понимаешь что ты делаешь можно ставит окна округления на порядки больше. Я, например, свои лучшие сети учил при 0,999, с соответсвующей скоростью, конечно. Более того, когда ты делаешь отжиг, например, ты можешь не уменьшать скорость каждый раз, а оставлять скорость той же, но увеличивать окно округления. Результат по локальным минимумам такой же, а скорость схождения на порядки выше. Объяснение механизма в мегакомменте выше.
2) График ошибки в самом конце статьи — самая дезориентирующая вещь на свете. Я даже когда-то хотел написать статью с названием «Обучение вашей нейросети начинается только после того как она уже сошлась». На самом деле после того, как ошибка уже вышла на полочку внизу если продолжить учить умело играя параметрами сети можно улучшить результат, например, в два раза. И вот то, на сколько её можно ещё после этого улучшить драматическим образом зависит от алгоритма и способа обучения. Обычное обучение полной выборкой без минибатча или методы второго порядка намертво зависают в первых же большого размера локальных минимумах и после выхода на полку дальше уже, практически, не учатся. SGD при постипенно снижающейся скорости даже без ничего больше может нащупать решение, например, в полтора раза лучше, перед этим конечно изрядно пометавшись по округе. А SGD с моментом с постепенно увеличивающимся окном например до 1000 и скоростью уменьшающейся например до 0.001 может найти места близкие по размерам к точности вычисления float в проце.
На сколько хороши или плохи другие упомянутые в статье алгоритмы после «выхода на полочку» — узнаю если найду время с ними поэкспериментировать. За что ещё раз спасибо.
И ещё интересно, применяются ли для обучения НС какие-то методы непохожие на модификацию SGD? Имитации отжига, или ещё какие-нибудь необычные?
В статье указано, что при некоторых параметрах оптимизаторы могут выскакивать из глобального минимума, и сказано что это проблема. Почему? Разве нельзя просто запоминать, где был достигнут минимум функции ошибок, и возвращаться туда?
Разумеется, можно. Так обычно и поступают, это называется обучение с возвратами. К сожалению, это сильно замедляет обучение, т.к. каждую эпоху приходится сохранять всю сеть. Этот приём не относится напрямую к оптимизаторам, его же используют и в других случаях, когда ошибка на валидационной выборке может возрастать.
И ещё интересно, применяются ли для обучения НС какие-то методы непохожие на модификацию SGD? Имитации отжига, или ещё какие-нибудь необычные?
Для имитации отжига слишком много параметров. Из интересного: RBM, но это уже не обычная нейронная сеть прямого распространения.
btw, мне казалось что просто скопировать веса сети в любом случае значительно дешевле чем посчитать градиент. А градиент мы так или иначе считаем каждый раз. Я не прав?
>методы непохожие на модификацию SGD
Раньше в почете были методы использующие приближенную вторую производную — сопряженные градиенты, BFGS. Сейчас вроде как применяют только SGD. Ибо быстро.
Использование не градиентных методов, ИМХО, не особо оправданно из-за огромного пространства поиска.
Разве нельзя просто запоминать, где был достигнут минимум функции ошибок, и возвращаться туда?и даже не оверфит самая большая проблема. Методы борьбы с ним, в конце концов, уже многочисленны. Дело в том.что чтобы узнать, что вы пришли в глобальный минимум вам нужно посчитать ошибку для всей имеющейся у вас выборки. А если ваша учебная выборка — несколько террабайт текстов из википедии это может быть немножечко затратно.
В процессе обучения обычно следят не за реальной ошибкой, а за скользящей средней ошибкой на обучающих батчах, подсчёт которой оказывается побочным продуктом обучения сети.
- Размер minibatch
- Алгоритм обучения
- Параметры, которые входят в алгоритм обучения. Как минимум learning rate: 1-5
- Регуляризация L1, L2, шум, ещё что-нибудь: 3-5
- Количество слоёв и нейронов в них. Тут можно очень здорово сузить количество вариантов, но всё равно это минимум два параметра: «толщина» и «глубина»
- Функции активации
- Если обучаем CNN, то размер окон свёртки и пулинга
- Если обучаем ансамбль, то размер ансамбля и способы его объединения
- Много всякой специфичной фигни
Даже если зафиксировать большую часть параметров (скажем, выкинем параметры отвечающие за архитектуру сети, а не за обучение), то всё равно будет параметров 5-10. Учтите, что сеть при обучении может засесть в плохом или хорошем локальном минимуме, поэтому хорошо бы её обучать хотя бы раза три и брать среднюю точность как fitting factor. Мне кажется, описанному эволюционному алгоритму понадобится итераций 50, чтобы сойтись хоть куда-нибудь (а вообще больше). Если предположить, что NN у нас несложная, и её обучение занимает пять минут, то 3*5*50 = 750 = 12.5 часов. Если же в меру сложная — час — то 3*60*50 = 9000 = 150 часов = 6 дней.
Итог: хорошо для экспериментирования на MNIST, плохо на практике, если у вас совершенно случайно нет вычислительного кластера.
Некоторые параметры, которые привычно считают неизменяемыми налету тоже можно менять при должной ловкости. Например, мутацией может быть дропаут или добавление нейрона в случайный слой. Только какую-то кроссвалидацию добавить чтобы алгоритм с добавлением нейронов не перебарщивал. А при остальных мутациях можно даже и без этого.
За нестерова не ручаюсь, а обычный SGD с моментом может много куда уползти после того как алгоритм казалось бы сошёлся. Как я писал в комментариях выше: «После того как ваша сеть сошлась обучение только начинается».
а и если обучать сеть с одними параметрами, затем изменить параметры, после чего продолжить обучать сеть — и получить какой-то хороший результат — это совсем не то же самое, что обучать сеть сразу со вторыми параметрами.
Простой пример. Берём достаточно сложную задачку с кучей минимумов, не ирисы, Учим GD minibatch. Размер пачки 100, скорость 0,05. Сеть куда-то сошлась, ошибка 0.35. Потом меняем параметры, 200/0.02, потом 200/0.01, потом 200/0.005, потом 500/0,005, потом 1000/ 0.001. Получаем сеть с ошибкой 0.22. Вопрос, могли бы мы туда попасть стартовав с параметрами 1000/0.001? Да никогда в жизни, — при таком маленьком уровне стахастики для нас первый же локальный минимум стал бы последним, и не видать нам ошибки 0.4 как своих ушей. Цифры близки к реальным, использовавшимся при обучении сети из моей статьи. Первичное схождение сети минут 20, полное обучение до конца — 8 часов, больше сеть уже не училась — ей синапсов нехватало на большее. Правда это времена на страшно тупо реализованной сетке, так что обращать внимание не на абсолютные значения времени, а только на соотношения.
Более широко известнай пример: того что, никаким обучением сразу с конечными параметрами вы не сможете достигнуть такого же результата, хоть 100 лет учите — современные сети для распознавания изображений:
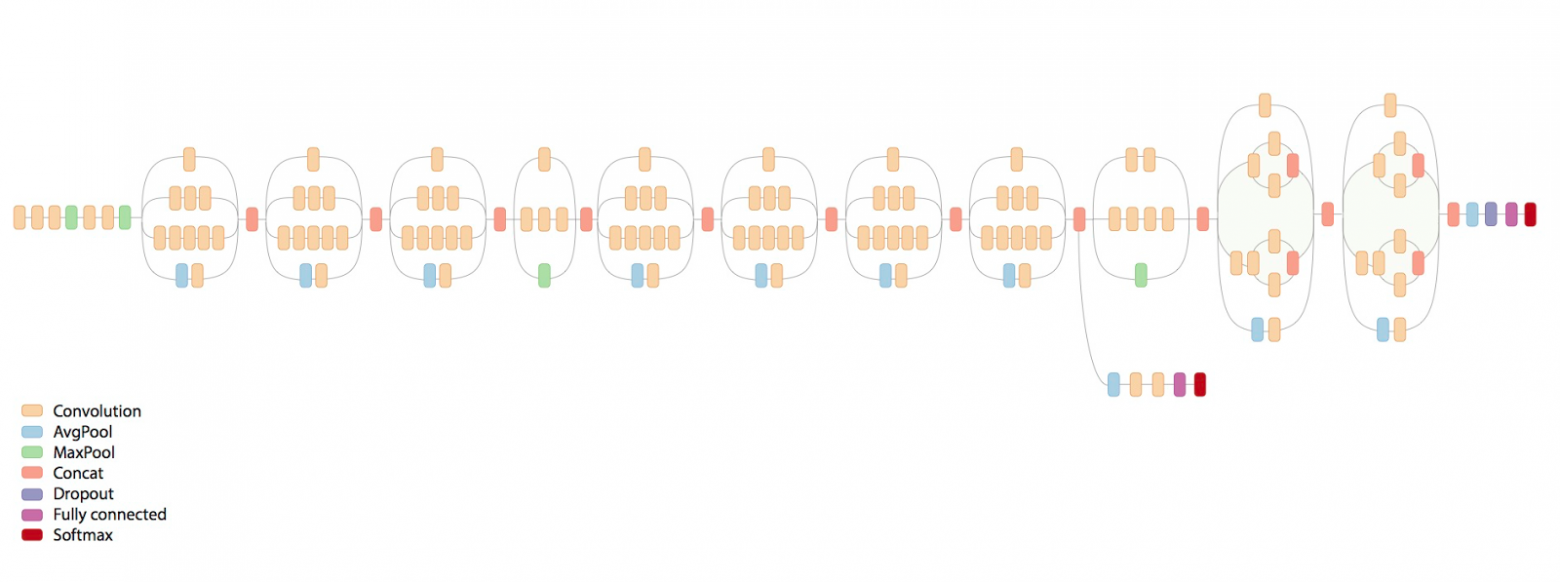 Если сразу учить всю эту гирлянду — эффект будет никакой. Берёте первый повторяющийся блок, к концу прикручиваете фулл-коннектед и софтмакс солои — учите. Потом отрубаете последние два слоя, до конката, вместо них добавляете ещё один повторяющийся блок и к нему фуллконнектед и софтмакс. Опять учите, и так 8 раз пока сеть не разрастётся до такой вот гирлянды. После чего добавляете на конец ещё одну надстройку с картинки и учите уже финально. Профит. Это я уже не конкретно эту сеть описывал, а вообще как учится весь класс сетей с такими архитектурами.
Если сразу учить всю эту гирлянду — эффект будет никакой. Берёте первый повторяющийся блок, к концу прикручиваете фулл-коннектед и софтмакс солои — учите. Потом отрубаете последние два слоя, до конката, вместо них добавляете ещё один повторяющийся блок и к нему фуллконнектед и софтмакс. Опять учите, и так 8 раз пока сеть не разрастётся до такой вот гирлянды. После чего добавляете на конец ещё одну надстройку с картинки и учите уже финально. Профит. Это я уже не конкретно эту сеть описывал, а вообще как учится весь класс сетей с такими архитектурами.Насчёт гирлянд, как на картинке: я, опять таки, согласен с итеративным способом обучения (занимался им и получил хорошие результаты), но не пойму причём тут эволюционные алгоритмы.
Впрочем, чего тут болтать — тут экспериментировать надо. Может, затухание скорости обучения действительно работает и не только на SGD, и мне просто тогда попались неудачные параметры сети или датасет с маленьким количеством минимумов/седловых точек.
Скорость большинство приведённых тут алгоритмов регулируют. А вот размер окна округления — нет. Про ценность окна округления тут: https://habrahabr.ru/post/318970/#comment_9998958
Если вы используете SGD с моментом можно менять момент. Если mini-batch — можно менять размер батчей. На самом деле это почти одно и то же.
Кроме того есть куча других параметров, которые можно менять. Параметры регуляризации, параметры дропаута. Параметры добавления нейронов, добавление слоёв, удаление промежуточных аутпутов. Это только из общепринятых параметров.
Эмм… С ResNet уже не так, промежуточные выходы блоков больше не нужны.
До ResNet и BatchNorm (и ReLU) это была скорее общая проблема с vanishing gradient, из-за которой нельзя было учить сильно многослойные сети (а до 2008 года из-за использования sigmoid эта же проблема была и с обучением сетей глубже 2 слоёв!).
Даже сразу неизменный learning rate в 0.001 достаточен, если каждый следующий слой не теряет большую часть этого градиента.
Karpathy это неплохо разбирает в
https://medium.com/@karpathy/yes-you-should-understand-backprop-e2f06eab496b
Глянтьте [1]. Вкратце — одна сеть выдает метапараметры обучения другой сети и обучается с подкреплением. Результаты очень хорошие, но еле-еле ползает. Имхо, эволюционные алгоритмы врядли сработают на каких-то больших моделях — это gradient-free метод оптимизации, которые работают на порядки медленнее gradient-based методов. То, что в [1], обучено с помощью gradient-based метода.
[1] https://arxiv.org/abs/1611.01578
А что касается неградиентных методов? Например метод бросания точек. Если я миллионы раз буду случайным образом выбирать параметры и смотреть, какой вариант лучше, не получится ли получить хороший результат?
Методы оптимизации нейронных сетей