Как стать автором
Поиск
Написать публикацию
Обновить

Винеровский хаос или Еще один способ подбросить монетку

Время на прочтение9 мин
Количество просмотров24K
Haskell*Математика*
Туториал

Теория вероятности никогда не переставала меня удивлять, начиная ещё с того момента, как я впервые с ней столкнулся, и до сих пор. В разное время в разной степени меня настигали, назовём их «вау-эффекты», шоковые удары в мозжечок, от которых меня накрывало эффектом третьего ока, и мир навсегда переставал быть прежним.

  • Первый «вау-эффект» я испытал от Центральной предельной теоремы. Берем кучу случайных величин, устремляем их количество в бесконечность и получаем нормальное распределение. И совсем неважно как распределены эти величины, неважно, будь это подбрасывания монетки или капли дождя на стекле, вспышки на Солнце или остатки кофейной гущи, результат будет всегда один — их сумма всегда стремится к нормальности. Разве что, нужно потребовать их независимость и существование дисперсии (позднее я узнал, что существует теорема и для экстремальных тяжелохвостых распределений с бесконечной дисперсией). Тогда этот парадокс долго не давал мне заснуть.
  • В какой-то момент учебы в университете такие предметы как дискретная математика и функциональный анализ слились вместе и всплыли в теорвере под видом выражения «почти наверное». Стандартный пример: вы случайно выбираете число от 0 до 1. С какой вероятностью вы ткнёте в рациональное число (привет, функция Дирихле)? Спойлер: 0. Ноль, Карл! Бесконечное множество не имеет никакой силы, если оно счетно. У вас бесконечное число вариантов, но вы не выберете ни один из них. Вы не выберете 0, или 1, или 1/2, или 1/4. Вы и не выберете 3/2.

    Да-да, что выбрать 1/2, что выбрать 3/2, вероятность нулевая. Вот только в 3/2 вы не ткнёте точно, таковы условия, а в 1/2 вы не попадёте ну… «почти наверное». Концепция «почти всюду»/«почти наверное» забавляет математика, а обывателя заставляет крутить пальцем у виска. Многие ломают себе мозг в попытке классифицировать нули, но результат того стоит.
  • Третий по счёту, но не по силе, «вау-эффект» настиг уже на переходе в advanced level
    — при чтении книг по стохастическим исчислениям. Причиной тому стала лемма Ито. Со времён школьной скамьи, когда нашим девственным глазам впервые показали производную, мы нисколько не сомневались в правильности вот такой вот формулы:

    $dX^2=2X\cdot dX.$

    И она верна. Вот только, если $X$ — это не случайный процесс. Адовая смесь из свойств нормального распределения и «почти наверное» доказывает, что в обратной ситуации эта формула в общем случае неверна. Томик мат.анализа с решениями обыкновенных дифференциальных уравнений теперь можно выкинуть в топку. Люди в теме тихо хихикают, остальные нетерпеливо листают статьи в Вики с исчислениями Ито.

Но совсем недавно я испытал и четвёртый, так называемый, «вау-эффект». Это не какой-то отдельно взятый факт, а целая теория, которую я собираюсь поведать в серии из нескольких статей. И если предыдущие финты теории вероятности вас уже не удивляют, то прошу милости под кат (знаю, вы и так уже здесь).

Полиномы Эрмита


Начнем с обыкновенной алгебры — определим «вероятностные» (они немного отличаются от «физических») полиномы Эрмита:

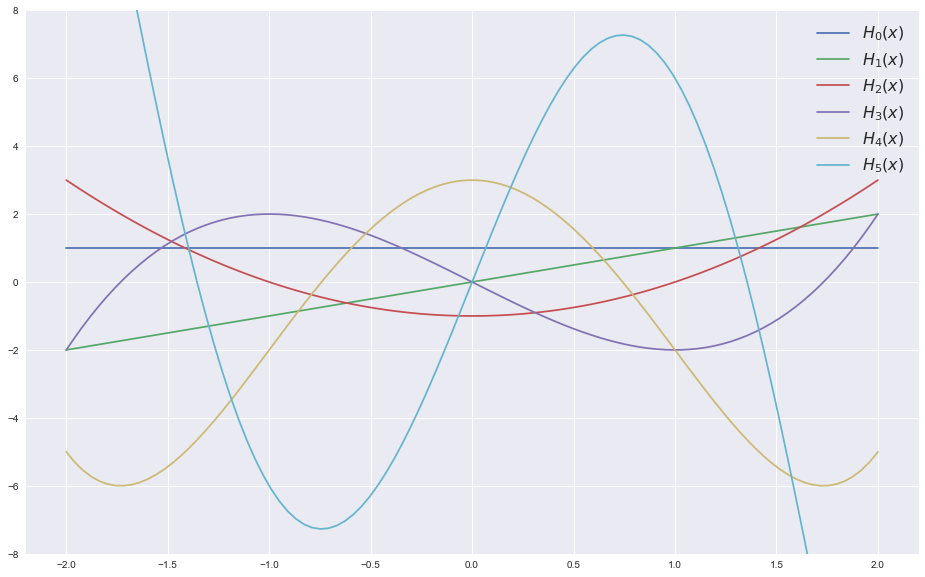
$H_n(x) = (-1)^ne^{x^2/2} \frac{d^n}{dx^n}(e^{-x^2/2}), \quad n \in \mathbb{N}_0.$

Значения первых полиномов: $H_0(x)=1, H_1(x) = x, H_2(x) = x^2-1, H_3(x)=x^3-3x, \dots$


Полиномы Эрмита обладают следующими свойствами:

  • $H_n'(x) = nH_{n-1}(x),$
  • $H_n(-x)=(-1)^nH_n(x),$
  • $H_{n}(x)=xH_{n-1}(x)-(n-1)H_{n-2}(x).$

Последнее соотношение поможет нам в вычислении $n$-ых полиномов Эрмита для заданного $x$. Программироваться мы будем на Haskell, ибо он позволяет математикам выражаться на привычном им языке — Haskell чист, строг и прекрасен как сама математика.

-- | 'hermite' is an infinite list of Hermite polynomials for given x
hermite :: (Enum a, Num a) => a -> [a]
hermite x = s
    where s@(_:ts) = 1 : x : zipWith3 (\hn2 hn1 n1 -> x * hn1 - n1 * hn2) s ts [1..]

Функция hermite принимает на вход параметр $x$, а на выходе даёт бесконечный лист из $n$-ых полиномов для $n=0,1,...$ Кто не знаком с концепцией ленивых вычислений, очень советую ознакомиться. Для тех же, кто эту концепцию знает, но ещё не до конца может в функциональное программирование: что здесь происходит? Представьте, что у нас уже есть бесконечный лист со всеми значениями Эрмитовых полиномов:

s = [1, x, x^2-1, x^3-3x, x^4-6x^2+3, ... ]

Хвост этого листа (без первого элемента):

ts = [x, x^2-1, x^3-3x, x^4-6x^2+3, ... ]

Вдогонку мы возьмем ещё лист с натуральными числами:

[1, 2, 3, ... ]

Функция zipWith3 комбинирует последние три листа, используя данный ему оператор:

x * [    x,  x^2-1,     x^3-3x, ... ]
  - [  1*1,    2*x,  3*(x^2-1), ... ]
  = [x^2-1, x^3-3x, x^4-6x^2+3, ... ]

Добавляем впереди 1 и x, и получаем полный набор Эрмитовых полиномов. Иными словами, мы достали лист со значениями полиномов, используя лист с этими значениями, то есть, лист, который мы и пытаемся достать. Поговаривают, что полное осознание красоты и мощи ФП сродни умению заглянуть себе в ухо.

Проверим: первые 6 значений для $x=1$:

Prelude> take 6 (hermite 1)
[1,1,0,-2,-2,6]

Что мы и ожидали увидеть.

Гильбертово пространство


Двинемся немного в другую степь — вспомним определение пространства Гильберта. Говоря научным языком, это полное метрическое линейное пространство с заданным на нём скалярным произведением $\langle X, Y \rangle$ На этом пространстве каждому элементу соответствует вещественное число, именуемое нормой и равное

$\| X\|=\sqrt{\langle X,X\rangle}.$

Ничего сверхъестественного. Когда я пытаюсь представить Гильбертово пространство, я начинаю от простого и постепенно прихожу к сложному.

  1. Самый простой пример — это пространство вещественных чисел: $H=\mathbb{R}$. В таком случае скалярным произведением двух чисел $X$ и $Y$ у нас будет

    $\langle X,Y \rangle=XY.$

  2. Затем я перехожу в Эвклидово пространство $H=\mathbb{R}^n$. Теперь

    $\langle X,Y\rangle=\sum_{i=0}^nX_iY_i.$

    Это пространство можно расширить до пространства комплексных векторов: $H=\mathbb{C}^n$, для которого скалярное произведение будет

    $\langle X, Y\rangle = \sum_{i=0}^nX_i\overline{Y_i}$

    (верхняя черта обозначает комплексное сопряжение).
  3. Ну и наконец прихожу в пространство для взрослых, пространство с бесконечной размерностью. В нашем случае это будет пространство квадратично интегрируемых функций, заданных на некотором множестве $\Omega$ с заданной мерой $\mu$. Мы будем его обозначать в виде $H=L^2(\Omega,\mu)$. Скалярное произведение на нем задается следующим образом:

    $\langle X, Y \rangle =\int_\Omega (X \cdot Y) d\mu.$

    Обычно под множеством $\Omega$ подразумевается интервал $[a,b]$, а под мерой $\mu$ — равномерная мера (мера Лебега), т.е. $d\mu=\mu(d\omega)=d\omega$. И тогда скалярное произведение записывается в виде обыкновенного интеграла Лебега

    $\int_a^bX(\omega)Y(\omega) d\omega.$

    Если же мы думаем в терминах теории вероятностей, то $\Omega$ — это пространство элементарных событий, $X=X(\omega)$ и $Y=Y(\omega)$ — случайные величины, а $\mu$ — вероятностная мера. У каждой такой меры есть своя функция плотности распределения $\rho$, которая может быть отличной от константы, тогда $d\mu=\rho(\omega)d\omega$ и скалярное произведение совпадает с математическим ожиданием:

    $\langle X, Y \rangle=\int_\Omega X(\omega) Y(\omega) \rho(\omega)d\omega = \mathbb{E}[XY].$




Гауссовский процесс


Настало время внести в наши размышления элемент случайности. Пусть у нас имеется гильбертово пространство $H$. Тогда мы назовем $\{W(h)\}_{h\in H}$ (изонормальным) Гауссовским процессом, если

  1. вектор из случайных величин $(W(h_1), \dots, W(h_n))$ распределен нормально с нулевым мат.ожиданием для любых $h_1, \dots h_n \in H$, и
  2. для $h,g \in H$

    $\mathbb{E}[W(h)\cdot W(g)] = \langle h, g \rangle.$


По своей математической сути $W(h)$ — это отображение из одного гильбертова пространства в другое, из некоторого $H$ в $L^2(\Omega, \mathcal{F}, \mathbb{P})$ — вероятностное пространство из случайных величин с конечной дисперсией, заданного триплетом $\Omega$ (множество элементарных событий), $\mathcal{F}$ (сигма-алгебра) и $\mathbb{P}$ (вероятностная мера). Несложно показать, что это отображение линейно:

$W(ah+bg)=aW(h)+bW(g) \quad \forall a,b \in \mathbb{R}, \forall h,g \in H.$

(в смысле равенства «почти наверное», привет «вау-эффект» #2)

Пример. Пусть $H=L^2((0,\infty), \lambda)$, где $\lambda$ — равномерная мера (Лебега). Скалярное произведение на нём

$\langle f, g\rangle=\int (f \cdot g) d\lambda.$

Пусть $h(s) = 1_{[0,t]}(s)$ — единичная функция на интервале $[0,t]$. Тогда $\| h\|^2 = \int 1_{[0,t]}(s)ds = t$ и

$B(t)=W(1_{[0,t]}) \sim \mathcal{N}(0,t)$

не что иное, как Броуновское движение (или Винеровский процесс). Более того,

$\int_0^t f(s)dB(s) = W(1_{[0,t]} f)$

называется интегралом Ито от функции $f$ относительно $B$.

Для того, чтобы реализовать Гауссовский процесс я воспользуюсь пакетами, которые благородные люди уже написали за нас.

import Data.Random.Distribution.Normal
import Numeric.LinearAlgebra.HMatrix as H

-- | 'gaussianProcess' samples from Gaussian process
gaussianProcess :: Seed                   -- random state
                -> Int                    -- number of samples m
                -> Int                    -- number of dimensions n
                -> ((Int, Int) -> Double) -- function that maps indices of the matrix into dot products of its elements
                -> [Vector Double]        -- m n-th dimensional samples of Gaussian process
gaussianProcess seed m n dotProducts = toRows $ gaussianSample seed m mean cov_matrix
  where mean = vector (replicate n 0)
        cov_matrix = H.sym $ (n><n) $ map (\i -> dotProducts (quot i n, rem i n)) [0..]

Функция gaussianProcess принимает параметр seed (стандартная штука для генераторов), nSamples — размер выборки, dim — размерность вектора $(h_1,…,h_n)^T$, dotProducts — функцию, принимающую на вход $(i,j)$, индекс матрицы ковариации и возвращающую соответствующее этому индексу скалярное произведение $\langle h_i,h_j\rangle$. На выход gaussianProcess выдает nSamples векторов $(W(h_1), \dots, W(h_n))$.


Уже подходит время объединить все полученные нами знания вместе. Но прежде, стоит упомянуть об одном полезном свойстве эрмитовых полиномов и нормального распределения в совокупности. Пусть $F(t,x)=\exp(tx-t^2/2).$ Тогда, используя разложение Тейлора,

$\begin{aligned} F(t,x)& = \exp(x^2/2-(x-t)^2/2) \\ &=\exp(x^2/2) \sum_{n=0}^\infty \frac{t^n}{n!t}\frac{d^n}{dt^n}\exp(-(x-t)^2/2)\bigg |_{t=0}\\ &= \sum_{n=0}^\infty t^n \frac{(-1)^n}{n!} \exp(x^2/2) \frac{d^n}{dz^n} \exp(-z^2/2)\bigg |_{z=x}\\ &=\sum_{n=0}^\infty \frac{t^n}{n!} H_n(x). \end{aligned}$

Возьмем $X, Y \sim \mathcal{N}(0,1)$ — две стандартные нормально распределенные случайные величины. Через производящую функцию нормального распределения мы можем вытащить следующее соотношение:

$\mathbb{E}[F(s,X)\cdot F(t,Y)]=\exp(st\mathbb{E}[XY]).$

Берем $(n+m)$-ую частную производную $\frac{\partial^{n+m}}{\partial s^n \partial t^m}$, приравниваем $s=t=0$ по обе стороны уравнения сверху и получаем

$\mathbb{E}[H_n(X) \cdot H_m(Y)] = \begin{cases} n!(\mathbb{E}[XY])^n, & n=m, \\ 0, & n \neq m. \end{cases}$


О чем это нам говорит? Во-первых, мы получили норму $\| H_n(X) \|^2=n!$ для $X \sim \mathcal{N}(0,1)$, а, во-вторых, мы теперь знаем, что разные эрмитовы полиномы от нормальных случайных величин ортогональны друг другу. Вот сейчас мы готовы к осознанию нечто большего.

Разложим пространство в хаос


Пусть $\mathcal{H}_n=\overline{\operatorname{span}}\Big \{ H_n(W(h)) \Big| \| h\| = 1 \Big\}$ — n-й Винеровский хаос. Тогда

$L^2(\Omega, \mathcal{F}, \mathbb{P}) = \bigoplus_{n=0}^\infty \mathcal{H}_n,$

где $\mathcal{F}$ — сигма-алгебра, созданная $W(h)$.

Воу-воу, палехче! Давайте разложим эту теорему о разложении по кусочкам и переведём с математического на человеческий. Мы не будем сильно вдаваться в детали, а лишь интуитивно поясним о чем тут речь. Значок $\operatorname{span}(X)$ обозначает линейную оболочку подмножества $X$ гильбертова пространства $H$ — пересечение всех подпространств $H$, содержащих $X$. Говоря проще, это множество всех линейных комбинаций элементов из $X$. Черта сверху над $\operatorname{span}$ обозначает замыкание множества. Если $\overline{\operatorname{span}}(X) = H$, то $X$ называется полным множеством (грубо говоря, "$X$ плотно в $H$"). Следовательно, $\overline{\operatorname{span}} \{ H_n(W(h)) | \| h\| = 1 \}$ — замыкание линейной оболочки полиномов Эрмита от Гауссовского процесса на единичной гиперсфере.

С нотацией вроде разобрались. Теперь о том, что такое Винеровский хаос. Идем от простого: $\mathcal{H}_0$ содержит все линейные комбинации Эрмитовых полиномов со степенью 0, то есть различные комбинации чисел $a\cdot 1$, то есть всё пространство вещественных чисел. Следовательно, $\mathcal{H}_0=\mathbb{R}$. Идем дальше. Несложно увидеть, что $\mathcal{H}_1= \{ W(h) | h \in H \}$, то есть пространство, составленное из Гауссовских процессов. Получается, что все центрированные нормальные величины принадлежат $\mathcal{H}_1$. Если мы добавим еще $\mathcal{H}_0$, то к ним присоединятся и остальные нормальные случайные величины, чье математическое ожидание отлично от нуля. Дальнейшие множества $\mathcal{H}_n$ уже оперируют с n-ми степенями $W(h)$.

Пример. Пусть $H=L^2((0,\infty), \lambda)$ и $X=B(t)^2$ — квадрат Броуновского движения. Тогда

$\begin{aligned} B(t)^2&=W(1_{[0,t]})^2 \\ & = \|1_{[0,t]} \|^2 \cdot W\bigg(\frac{1_{[0,t]}}{\|1_{[0,t]} \|}\bigg)^2 \\ & = t\cdot W\bigg(\frac{1_{[0,t]}}{\sqrt{t}}\bigg)^2\\ &=tH_2\bigg(W\bigg(\frac{1_{[0,t]}}{\sqrt{t}}\bigg)\bigg)+t. \end{aligned}$

Первое слагаемое принадлежит $\mathcal{H}_2$, второе — $\mathcal{H}_0$. Это и называется разложением в Винеровский хаос.

Мы показали ранее, что $\mathcal{H}_n \perp \mathcal{H}_m$ для $n \neq m$. Теорема о разложении гласит о том, что эти множества не только ортогональны друг другу, но также формируют полную систему в $L^2(\Omega, \mathcal{F}, \mathbb{P})$. Что это означает на практике? Это значит, что любая случайная величина $X$ с конечной дисперсией может быть аппроксимирована полиномиальной функцией от нормально распределенной случайной величины.

На самом деле
На самом деле, такое разложение полезно, если распределение $X$ в определенном смысле близко к распределению нормальному. Например, если мы имеем дело с Броуновским движением или с логнормальным распределением. И мы не просто так упомянули, что $\mathcal{F}$ создаётся $W(h)$, это очень важное условие. В действительности, плотность нормального распределения

$\rho(x)=\frac{1}{\sqrt{2\pi}}e^{-x^2/2}$

очень схожа с определением полинома Эрмита

$H_n(x) = (-1)^ne^{x^2/2} \frac{d^n}{dx^n}(e^{-x^2/2}), \quad n \in \mathbb{N}_0.$


Если же распределение $X$ далеко от Гаусса, то можно попробовать и другие ортогональные полиномы. Например, плотность Гамма-распределения:

$\rho(x)=\frac{x^{n-1} e^{-x}}{\Gamma(n)}.$

Ничего не напоминает? Да это же полиномы Лагерра

$L_n(x) = \frac{e^x}{n!}\frac{d^n}{dx^n}(x^ne^{-x})$


Равномерному распределению соответствуют полиномы Лежандра, биномиальному распределению — полиномы Кравчука, и т.п. Теория, развивающая идею разложения вероятностного пространства на ортогональные полиномы именуется в англоязычной литературе как «Polynomial chaos expansion».

Пример. Давайте теперь возьмем $H=\mathbb{R}$, функцию $f$ и зададим случайную величину $X$, такую что

$X=f(\xi) \in L^2(\Omega, \mathcal{F}, \mathbb{P}),$

где $\xi = W(1) \sim \mathcal{N}(0,1)$. По теореме о разложении мы можем представить её в виде взвешенной суммы из полиномов Эрмита

$f(\xi)=\sum_{n=0}^\infty f_nH_n(\xi),$

где коэффициенты задаются формулой

$f_n=\frac{1}{n!}\mathbb{E}[f(\xi) \cdot H_n(\xi)].$

Эти значения $f_n$ мы получили следующим образом:

$\begin{aligned} \mathbb{E}[f(\xi)\cdot H_n(\xi)] & = \langle f(\xi), H_n(\xi) \rangle \\ &= \langle \sum_{k=0}^\infty f_k H_k(\xi) , H_n(\xi) \rangle \\ &= \sum_{k=0}^\infty f_k \langle H_k(\xi), H_n(\xi) \rangle \\ & = f_n \| H_n(\xi) \|^2 = f_n n!. \end{aligned}$

Поздравляю! Теперь, если у вас есть функция от стандартной нормально распределенной случайной величины, вы сможете её разложить по базису из Эрмитовых полиномов. Например, подбрасывание честной монетки 0-1 мы можем представить в виде

$X=1_{(0,\infty)}(\xi).$

Немного поколдовав с математикой (подсчет несложных интегралов мы оставим читателю), мы получаем разложение:

$X= \frac{1}{2} + \frac{1}{\sqrt{2\pi}} \sum_{n=0}^\infty \frac{(-1)^n}{2^n(2n+1)n!} H_{2n+1}(\xi). $


Заметьте, что каждый второй элемент в разложении по базису равен нулю. 

-- | 'second' function takes a list and gives each second element of it
second (x:y:xs) = y : second xs
second _ = []

-- | 'coinTossExpansion' is a Wiener chaos expansion for coin-toss r.v. to n-th element
coinTossExpansion :: Int    -- number of elements in the sum
                  -> Double -- gaussian random variable
                  -> Double -- the sum
coinTossExpansion n xi = sum (take n $ 0.5 : zipWith (*) fn (second $ hermite xi))
    where fn = 1.0 / (sqrt $ 2 * pi) : zipWith ( \fn1 k -> -fn1 * k / ((k + 1) * (k + 2)) ) fn [1, 3..]

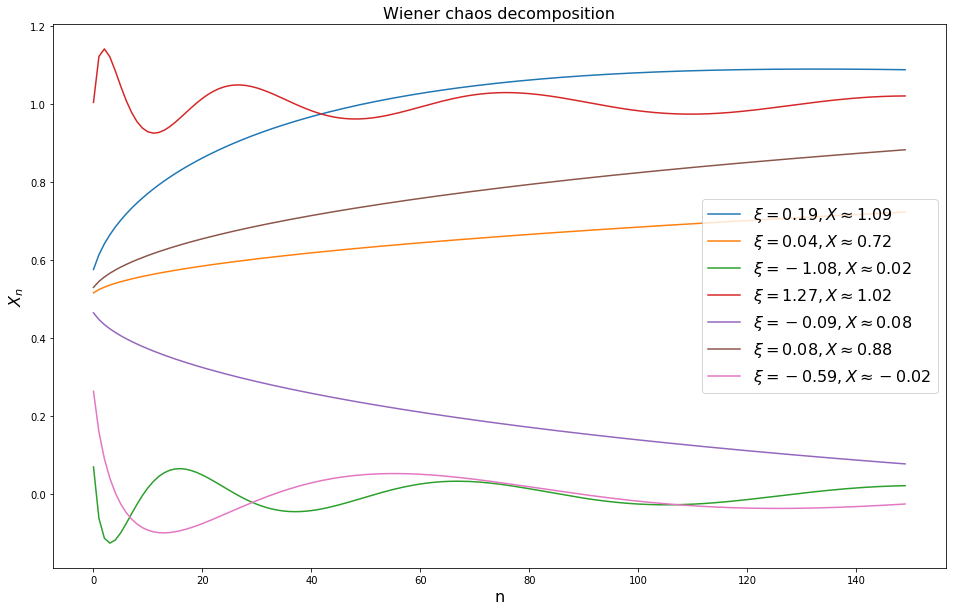
Функция coinTossExpansion возвращает сумму, полученную разложением случайной монетки в винеровский хаос, для данного $\xi$ от $0$ до $n$. На графике показана постепенная сходимость для выбранных случайным образом $\xi$ с возрастанием $n$.


Судя по этому графику, где-то после $n \approx 100$ мы можем обрезать сумму, округлить и вернуть в качестве $X$.

-- | 'coinTossSequence' is a coin-toss sequence of given size
coinTossSequence :: Seed  -- random state
                 -> Int   -- size of resulting sequence
                 -> [Int] -- coin-toss sequence
coinTossSequence seed n = map (round.coinTossExpansion 100) (toList nvec)
    where nvec = gaussianProcess seed n 1 (\(i,j) -> 1) !! 0

Проверим, как будет выглядеть последовательность из 20 подбрасываний.

Prelude> coinTossSequence 42 20
[0,0,1,0,0,0,1,1,0,1,0,0,0,1,0,1,1,1,0,1]

Теперь, когда вас попросят сгенерировать подбрасывания монетки, вы знаете, что им показать.


Ну а без шуток, мы что-то посчитали и что-то разложили, а какой в этом всем толк, спросите вы. Не спешите чувствовать себя обманутыми. В последующих статьях мы покажем, как это разложение позволяет брать производную от случайной величины (в некотором смысле), расширим стохастическое интегрирование (и ваше сознание), и найдем всему этому практическое применение в машинном обучении.
Только зарегистрированные пользователи могут участвовать в опросе. Войдите, пожалуйста.
Впечатления от статьи:
83.28% Я ничего не понял, продолжай!239
5.57% Я ничего не понял, не продолжай!16
10.8% Я все понял, продолжай!31
0.35% Я все понял, не продолжай…1
Проголосовали 287 пользователей. Воздержался 41 пользователь.
Теги:
Хабы:
Всего голосов 47: ↑45 и ↓2+43
Комментарии25
88
Карма
0
Рейтинг
Александр Самарин @The_Freeman

Математик-реалист

Отправить сообщение
Github

Публикации

Ближайшие события

Ваш аккаунт

Разделы

Информация

Услуги

Техническая поддержка
© 2006–2025, Habr