Как стать автором
Поиск
Написать публикацию
Обновить

Многоканальная атрибуция глазами Calltouch

Время на прочтение19 мин
Количество просмотров19K
Веб-аналитика*

Введение


В последние годы инструментарий современного интернет-маркетолога расширяется все более и более быстрыми темпами. Сегодня помимо поисковой оптимизации ($SEO$) и контекстной рекламы Яндекс Директ и $Google\:Adwords$ в практический обиход вошли $e-mail$ каналы, социальные сети, $Instagram$, ремаркетинг/ретаргетинг и т. д. Поэтому перед маркетологом встает задача выбора тех рекламных каналов, которые будут наиболее эффективны для конкретного проекта. Calltouch решил поговорить о том, что помимо сложности выбора оптимальных рекламных каналов, достаточно сложным становится вопрос комплексной оценки эффективности того или иного канала для последующего распределения рекламного бюджета между ними. Колонка старшего менеджера по продукту Calltouch Федора Иванова mthmtcn.

По оценке Calltouch cложность эта связана в первую очередь с тем, что пользователь со своей стороны обладает по сути тем же самым инструментарием, что и маркетолог: он может прийти на сайт как по прямой ссылке, так и по переходу из соцсетей, из рекламной выдачи Яндекса и. т. д. Более того, прежде чем совершить на сайте целевое действие (конверсию) пользователь может неоднократно посещать сайт из разных «точек входа»: первый раз он перешел на сайт, кликнув по рекламному объявлению ($CPC$), которое Яндекс выдал по его поисковому запросу, второе посещение было по прямому переходу ($Direct$), ну а третье (приведшее к конверсии — $C$ ) было из социальной сети ($Social$) в этом случае мы наблюдаем цепочку (многоканальную последовательность):

$CPC → Direct → Social → C$



Таким образом, при оценке эффективности рекламных каналов маркетологу прежде всего необходимо ответить на вопрос: как оценить вклад того или иного источника на формирование конверсии на сайте? По-другому этот вопрос можно сформировать так: что случится с конверсией на сайте, если исключить тот или иной маркетинговый канал? Для ответа на данный вопрос существует ряд методологий, которые называются моделями атрибуции. Рассмотрим эти модели более подробно.

Модели атрибуции


Модель атрибуции – это способ распределения «веса» конверсии между каналами. В зависимости от выбора модели атрибуции будет рассчитан вес канала (источника), который условно можно считать тем вкладом, который данный источник внес в формирование конверсии. С данными моделями сталкивался практически каждый пользователь Яндекс Метрики или Google Analytics (раздел «многоканальные последовательности»). В настоящее время выделяют следующие основные модели атрибуции:

  • По последнему взаимодействию (последнее непрямое взаимодействие, последний клик в AdWords, последний значимый переход) – $Last\:Click\:Model\:(LCM)$
  • Первое взаимодействие – $First\:Click\:Model\:(FCM)$
  • Линейная модель – $Linear\:Model\:(LM)$
  • Временной спад – $Time\:Decay\:Model\:(TDM)$
  • На основе позиции – $Position\:Type\:Model\:(PTM)$

Как уже было отмечено, основное отличие моделей атрибуции между собой – это способ расчета веса канала в последовательности. Рассмотрим каждую модель более подробно. Для наглядности предположим, что мы имеем следующую многоканальную последовательность:

$AdWords→CPC →Social →E-mail →Yandex →CPC → Direct →C$


Last Click Model


Данная модель ввиду своей простоты и интуитивной «корректности» получила наибольшее распространение на практике. В самом общем случае в рамках $LCM$ модели все $100%$ веса конверсии отдаются последнему каналу в многоканальной последовательности, который предшествовал факту наступления целевого действия. В нашем случае классическая $LCM$ модель даст вес $100%$ каналу $Direct$ и $0%$ всем остальным каналам.

На практике встречаются различные разновидности $LCM$ модели, все они отличаются друг от друга тем, как выбирают «последний» канал. Приведем таблицу, которая демонстрирует метод выбора канала в зависимости от разновидности модели:


First Click Model


В данной модели $100%$ вес отдается первому источнику в последовательности и $0%$ всем остальным. В нашем случае максимальный вес получит источник $Direct.$ Если модель $LCM$ “максимизирует” вес последнего канала, который «побуждает к действию», то $FCM$ модель отдает предпочтение каналу, который начинает цепочку, т. е. «пробуждает интерес» пользователя к сайту. Данная модель также используется на практике, хотя и значительно реже, чем $LCM.$

Linear Model


Линейную модель ($LM$), а также ее обобщения и улучшения (модель временного спада и на основе позиции) объединяет прежде всего то, что в ее рамках все каналы получают свой ненулевой вес. Различие между моделями заключается только в способе распределения веса между всеми каналами. В случае $LM$ все каналы получают одинаковый вес (то есть их вклады в формирование конверсии) считаются равнозначными. В нашем случае каналы $AdWords\:CPC,$ $Social,$ $E-mail,$ $Yandex\: CPC,$ $Direct$ будут иметь вес $100/5=20$%.

Time Decay


Модель атрибуции $TDM$ ($Time\:Decay\:Model$) базируется на предположении, что вклад канала тем больше, чем “ближе” к конверсии он находится, таким образом, вес канала является монотонно возрастающей функцией от его позиции в цепочке. По ссылке можно ознакомиться с формулой расчета веса канала.

Position Type Model


Модель атрибуции $PTM$ является комбинацией из трех моделей: $LCM,$ $FCM$ и $LM.$ В ее рамках по максимальную долю (как правило по $40%$) получают первое и последнее взаимодействия в цепочке, а остальные (как правило $20%$) равномерно (как в линейной модели) распределяются между промежуточными каналами. В нашем примере каналы $AdWords\:CPC$ и $Direct$ получат по $40%$ веса, а $Social,$ $E-mail,$ $Yandex\:CPC$ по $6.67%.$

Как выбрать модель атрибуции?


Выбор модели атрибуции – важнейший этап в оценке эффективности рекламы. В зависимости от модели аналитик может получать абсолютно противоположные выводы о рентабельности того или иного канала. Особенно явно это наблюдается в тематиках, где процесс принятия решения занимает достаточно много времени (например, в сфере недвижимости или в автомобильной тематике). Возникает естественный вопрос: какую модель атрибуции следует принимать за эталон? К сожалению, однозначного ответа на этот вопрос не существует. Только глубокий анализ поведения пользователей на сайте (пользовательских сессий) позволит принять взвешенное решение о выборе той или иной методике привязки конверсий к источнику трафика.

Как правило выбор останавливается на модели $LCM,$ однако на практике мы сталкивались с ситуациями, когда замена $LCM$ на $PTM$ c последующим распределением средств между каналами позволяла существенно увеличить эффективность маркетинговых мероприятий.

Отдельно стоит отметить, что модель атрибуции является важнейшим фактором, который стоит учитывать при оптимизации контекстной рекламы. Выбор модели напрямую влияет на статистику, которая используется для расчета ставок. Если же считать, что каждая ключевая фраза – это отдельный рекламный канал, то можно существенно обогатить статистику, которая поступает на вход оптимизатора, кроме того, анализ последовательных переходов пользователя между ключевыми словами позволит увеличить эффективность оптимизации. Обсуждению этой темы будет посвящена отдельная глава данной работы.

Прежде чем перейти к описанию подхода, используемого нами для анализа многоканальных последовательностей, приведем «шуточный» пример, который с одной стороны покажет ограниченность классических моделей атрибуции, а с другой стороны позволит сформировать те основные вопросы, на которые следует найти ответ.

Допустим, целью является C=«увезти девушку к себе домой, чтобы посмотреть кино» .

Предположим, что мы имеем следующую цепочку действий (по сути каналов), которые привели к желаемой цели:

Познакомиться с девушкой → Пригласить в кино → Подарить цветы → Гулять вместе в парке → Проводить до дома → Пригласить на свидание в ресторан → Подарить цветы → Угостить ужином → Угостить коктейлем → Угостить еще одним коктейлем →… и еще одним → рассказать анекдот → C

Если мы имеем дело с моделью $LCM,$ то считаем, что для достижения поставленной цели нам в принципе было достаточно обойтись анекдотом. Если считать в рамках модели $FCM,$ то успех гарантирован, как только мы познакомились (что более похоже на правду в сравнении с тем же анекдотом). Модель $LM$ предполагает, что все действия внесли равный вклад. Модель $PTM$ постулирует, что наибольший вклад имеют факт знакомства и анекдот (причем в равных долях), а влияние остальных факторов незначительно. Наконец, $TDM$ считает, что каждое наше следующее действие «подогревало» интерес девушки, тем самым увеличивая вероятность достижения конечной цели, но все же анекдот был решающим фактором.

Как мы видим, ни одна из классических моделей не может адекватно описать рассмотренную выше ситуацию и тем более не позволит правильно ответить на вопрос, какой же канал (действие) оказалось наиболее важным на самом деле.

Теперь сформулируем основные вопросы, на которые бы хотелось получить ответы от модели атрибуции:

  • Достаточно ли просто рассказать анекдот? И если да, то как часто?
  • Насколько в принципе типична практика рассказывания анекдотов для достижения цели?
  • Что будет если не рассказывать анекдот?
  • Можно ли заменить анекдот на какое-либо другое действие? Если да, то на какое следует заменить?

Для правильного ответа на большинство поставленных вопросов нам недостаточно рассмотреть только одну последовательность. Требуется собрать некоторую статистику, которая бы с одной стороны позволяла прогнозировать поведение пользователей, а с другой – позволяла бы оценить вероятность конверсии на сайте для каждой из точек взаимодействия.

Рассматриваемая нами модель изначально разрабатывалась для совокупной оценки многоканальных последовательностей, предполагая, что каналы являются взаимо-зависимыми. Она позволяет ответить на большинство из сформулированных выше вопросов. Кроме того, мы покажем, как описанные нами методы позволят прогнозировать коэффициент конверсии по каждой ключевой фразе, что является необходимым элементом в оптимизации ставок в контекстной рекламе.

Прежде всего опишем тот формат данных, с которым работает наша модель.

Пользовательские сессии


Предположим, что за некоторый анализируемый нами промежуток времени $T$, на сайт было совершено $M$ переходов, то есть мы располагаем данными об $M$ пользовательских сессиях. Каждая $i$ сессия $S_i$ обладает фиксированным набором параметров (атрибутов сессии) $P$. Для нашего анализа нам потребуется, чтобы следующее множество атрибутов входило во множество всех атрибутов сессии:

$A=\{SrcType,\:TimeS,\:TimeF,\:URL,\:clientID,\:CVtype \} \subset P,$


где:

  • $SrcType$– канал, по которому был совершен переход на сайт
  • $TimeS$– время начала сессии
  • $TimeF$ — время окончания сессии
  • $URL$ — адрес страницы, на которую попал пользователь при переходе на сайт
  • $clientID$– уникальный идентификатор пользователя
  • $CVtype$– была ли совершена конверсия в результате сессии ( $CV$– да, $N$– нет)

Далее для простоты мы будем полагать, что промежуток времени $[TimeS; TimeF]$ находится внутри анализируемого периода $T$, поэтому мы уберем атрибуты $TimeS,\:TimeF$ из рассматриваемого множества параметров. Также следует отметить, что параметр $URL$ требуется только для того, чтобы осуществить переход от уровня каналов до уровня ключевых фраз (при условии наличия разметки в $URL$), что пригодится для оптимизации ставок, но не обязательно для оценки влияния каналов на конверсию. Под каналом мы понимает источник трафика, к которым можно отнести:

  • Yandex CPC
  • Google CPC
  • Facebook
  • Vkontakte
  • Instagram
  • Direct
  • Referal
  • и т. д.

Для простоты изложения будем кодировать рекламные каналы следующим образом: $c_1,\:c_2,\:...,\:c_k$, считая, что их количество ограничено величиной $k$.

Теперь предположим, что $M$ сессий $\Sigma=\{S_1,S_2,...,S_M\}$ были инициированы $G\leq M$пользователями. При помощи уникального идентификатора пользователя $clientID$ можно разбить множество $\Sigma$ на $G$ непересекающихся подмножеств:

$\Sigma=U_1\cup U_2…\cup U_G,$


где $U_i$ множество сессий (отсортированных по возрастанию даты окончания) с одинаковым $clientID$, т. е. множество упорядоченных в хронологическом порядке сессий, инициированных одним и тем же пользователем. Учитывая наше предположение о том, что $[TimeS; TimeF]\subset T$, то на основании данных в $U_i$ мы можем сопоставить с каждым $i$ пользователем следующую цепочку каналов:

$c_{i1}→c_{i2}→...→c_{iL_i},$


где $L_i=|U_i|$ — количество элементов (по сути количество переходов пользователя на сайт) во множестве $U_i$. Представленная выше цепочка переходов представляет из себя последовательность источников трафика, которые использовал $i$ пользователь в процессе взаимодействия с сайтом.

Введем два дополнительных «псевдоканала» $CV$ и $N$ по правилу:

  • Если во время сессии $i$ пользователя с источником $c_{ij}(1\leq j\leq L_i)$ произошла конверсия, то после $c_{ij}$ добавим $CV$, получив $...→c_{ij}→CV→...$
  • Если в результате последней текущей сессии $i$ с источником $c_{iL_i}$ конверсии не произошло, то после $c_{iL_i}$ добавим $N$, получив $...→ c_{iL_i}→N$

Кроме того, дополнительно обратим внимание на ситуацию, когда мы имеем дело с цепочками вида:

$ ...\rightarrow c_{ij}\rightarrow CV\rightarrow...\rightarrow CV\rightarrow... $


Последовательности с такой структурой не могут возникнуть согласно сформулированным выше правилам, но тем не менее могут иметь место в ряде случаев, например в звонящих тематиках, когда помимо указанных выше параметров сессии мы имеем уникальную связку:

$clientID → TelNumber$



В этом случае первый звонок в указанной выше цепочки будет уникальным звонком, а все последующие – повторными звонками абонента с заданным $clientID$. Такие цепочки будут учитываться в нашей модели в том случае, если помимо информации о переходах на сайт, ведется «журнал» взаимодействий пользователя с сайтом в том числе в офлайн режиме (например, журнал звонков).

Отметим ключевую особенность рассмотренной выше методики формирования цепочек взаимодействия пользователя с сайтом. Она заключается в том, что любая цепочка взаимодействия (многоканальная последовательность) всегда оканчивается одним из двух «событий»: $CV$ или $N$. При этом событие $N$ может встретиться только в конце последовательности, в то время как $CV$ может появиться на произвольном месте.

Приведем типичные примеры последовательностей, сформированных по описанным правилам. Для простоты ограничимся 3 различными каналами $c_1,\:c_2,\:c_3$, к которым добавим $CV$ и $N:$

  • $c_1→N$
  • $c_1→c_2→N$
  • $c_1→CV$
  • $c_1\rightarrow c_2\rightarrow CV\rightarrow c_1\rightarrow N$
  • $c_1\rightarrow c_2\rightarrow CV\rightarrow c_3\rightarrow N$
  • $c_1→c_2→CV→CV$
  • $c_1\rightarrow c_2\rightarrow CV\rightarrow CV\rightarrow c_3\rightarrow N$

Cледующий шаг, необходимый для построения мультиканальной модели атрибуции заключается в том, чтобы преобразовать последовательности таким образом, чтобы событие $CV$, как и $N$, могло встречаться только строго в конце последовательности (такие последовательности будем называть элементарными). Для этого будем «расщеплять» исходные цепочки так, чтобы в их конце всегда стояли $CV$ или $N$.

Продемонстрируем эту методику на примере типичных последовательностей:

  • цепочки 1-4 уже приведены к «элементарному» виду
  • цепочку 5 «расщепим» на: $c_1→c_2→CV$ и $c_1→c_2→c_1→N$
  • цепочку 6 «расщепим» на: $c_1→c_2→CV$ и $c_1→c_2→c_3→N$
  • цепочку 7 «расщепим» на: $c_1→c_2→CV$ и $c_1→c_2→CV$
  • цепочку 8 «расщепим» на: $c_1→c_2→CV$, $c_1→c_2→CV$ и $c_1→c_2→c_3→N$

В результате расщепления все цепочки стали «элементарными», и теперь мы можем приступить к описанию модели. Однако прежде чем перейти к этому шагу, мы уже на данном этапе можем ответить на вопрос: как оценить влияние канала на конверсию на сайте.

Расчет влияния каналов на конверсию


Рассмотрим множество из $G$ последовательностей (будем считать, что все они уже являются элементарными, то есть оканчиваются на $CV$ или $N$. Предположим, что из последовательностей $X$ оканчиваются на $CV$ и $G$ — $X$ на $N$. Обозначим влияние канала $c_i$ на конверсию на сайте за промежуток времени $T$ через $I(c_i)$, а элементарную $j$ цепочку через $R_j$. Величину влияния $I(c_i)$ канала $c_i$ на конверсию будем считать как количество «недополученных» конверсий в случае удаления канала $c_i$ из всех конверсионных цепочек, где он присутствует, отнесенное к общему количеству конверсий $X$:

$I(c_i)=\frac{|\{R_j│c_i\in R_j,\:CV\in R_j\}|}{X}$


Очевидно, что для любого $c_i$ величина $I(c_i)$ удовлетворяет следующему неравенству:

$0\leq I(c_i)\leq 1$

причем $I(c_i)=0$ тогда и только тогда, когда канал $c_i$ не входит ни в одну «конверсионную» последовательность, и $I(c_i)=1$ в том и только том случае, если удаление $c_i$ приведет к потере всех конверсий на сайте. Таким образом, легко оценить новое число конверсий, которое получится после удаления канала $c_i$:

$CV_{new}=X*(1-I(c_i))$


Рассчитаем влияния каналов $c_1$, $c_2$, $c_3$ для нашего примера. Всего мы наблюдаем $8$ конверсий (конверсионных цепочек) из $13$ элементарных цепочек $R_j$. Канал $c_1$ участвует во всех конверсионных цепочках, а значит его влияние на конверсию равно $1$: $I(c_1)=1$. Далее, канал $c_2$ присутствует в $7$ конверсионных цепочках, а значит $I(c_2)=7/8.$ Наконец, $c_3$ входит в состав одной конверсионной цепочки, тогда $I(c_3)=1/8.$

Легко заменить, что сумма влияний каналов не равна единице. Для удобства можно ввести нормировку и считать нормализованное влияние $I_n(c_i)$ каналов на конверсию:

$I_n(c_i)=\frac{I(c_i)}{\sum\limits_{i=1}^k I(c_i)}.$


В этом случае, очевидно

$\sum\limits_{i=1}^k I_n(c_i)=1.$


Формула для расчета влияния канала на конверсию может быть легко модифицирована на случай, когда требуется оценить влияние одного канала на другой. В частности, если стоит задача выяснить, как влияет канал $c_i$ на $c_j$, то можно воспользоваться следующим рассуждением: сессия пользователя, инициированная каналом $c_i$ приводит к сессии с каналом $c_j$ столько раз, сколько существует цепочек $R_f$, таких что в них $c_i$ предшествует $c_j$. Тогда если обозначить через $I(c_i,c_j)$ величину такого влияния, то:

$I(c_i,c_j )=\frac{|\{R_f│c_i,c_j\in R_t\:and\: c_i\:precede\:c_j\}|} {|\{R_t│c_j\in R_t \}|}.$


В общем случае функция $I(c_i,c_j)$ не является симметричной: $I(c_i,c_j)≠I(c_j,c_i).$ Последовательности $R_f$, такие что в них одновременно $c_i$ предшествует $c_j$ и $c_j$ предшествует $c_i$ (т. е. образуются циклы) также можно учитывать в знаменателе формулы. Введенная ранее нормировка естественным образом обобщается и на только что описанный более общий случай:

$I_n(c_i,c_j)=\frac{I(c_i,c_j)}{\sum\limits_{h=1}^k I(c_i,c_h) }.$



Оценка изменения базовых метрик при отключении канала


Ответив на вопрос, как изменится количество конверсий при удалении из всех цепочек того или иного канала $c_i$ возникает вполне естественный вопрос о том, как изменится значение таких базовых метрик, используемых при анализе эффективности рекламы, как:

  • расход
  • стоимость конверсии (CPA)

Ответить на данные вопросы, не привлекая дополнительные допущения, достаточно сложно. Наша базовая аксиома состоит в том, что при удалении канала $c_i$ из некоторой цепочки $R_j$, данная цепочка прерывается. Более точно формулировка выглядит так: если цепочка до удаления канала имела вид:

$R_j=\{ c_{i1}\rightarrow c_{i2}\rightarrow ...\rightarrow c_{ik}\rightarrow c_i\rightarrow c_{i(k+1)} \rightarrow ...\},$

то после удаления канала $c_i$ цепочка будет модифицирована в:

$ R_j \rightarrow R_j^{new}=\{ c_{i1}\rightarrow c_{i2}\rightarrow ...\rightarrow c_{ik}\rightarrow N\}. $


Данное допущение означает, что если убрать канал, который был использован пользователем для взаимодействия с сайтом, то дальнейшего взаимодействия пользователя с данным сайтом не будет.

Для оценки базовых метрик нам также необходимо добавить в параметры сессий пользователей такой показатель как «стоимость перехода». Eго можно интерпретировать как стоимость, которую платит рекламодатель, за клик пользователя по данному каналу, если канал бесплатен (как например прямой переход), то будем считать, что стоимость перехода равна $0.$ Если возможно установить только общую стоимость затрат на канал (как например для $SEO$), то будем полагать, что стоимость перехода в конкретной сессии равна отношению общих затрат на канал к количеству использований этого канала по всем сессиям. Будем обозначать стоимость перехода для канала $c_i$ в цепочке $R_j$ через $V_j(c_i)$. Таким образом, мы можем оценить стоимость $V(R_j)$ одной цепочки $R_j$ следующим образом:

$V(R_j )=\sum\limits_{c_i\in R_j}{V_j(c_i)}.$


При этом общие расходы на канал $c_i$ равны:

$V(c_i )=\sum\limits_{j:c_i\in R_j}{V_j(c_i)}.$


Oбщие расходы на привлечение пользователей на сайт при использовании каналов $c_1,c_2,..., c_k$ равны:

$V=\sum\limits_{j=1}^G\sum\limits_{c_i\in R_j}{V_j (c_i)} = \sum\limits_{i=1}^k\sum\limits_{j:c_i\in R_j}{V_j(c_i)}.$


Двойственность формулы объясняется разными способами вычисления общих расходов: в первом случае мы суммируем расходы на каждую из цепочек по всем $G$ цепочкам, а во втором – суммируем расходы на канал по всем $k$ каналам.

Для оценки новых расходов после удаления из всех цепочек канала $c_i$ кажется наиболее очевидным воспользоваться формулой:$V_{new}=V_{old}-\sum\limits_{j:c_i\in R_j}{V(R_j)},$ где $V_{new}$ — новый расход после удаления канала $c_i$, а $V_{old}$ — прежний расход. Однако, такая простая логика не приводит к правильной оценке расходов по той причине, что в тех цепочках $R_j$, где встречается $c_i$, перед ним могли быть задействованы другие, не удаленные каналы. Таким образом, для более точной оценки, нам необходимо учитывать стоимость «усеченных» цепочек. Поэтому:

$V_{new}=V_{old}-\sum\limits_{j:c_i\in R_j}\sum\limits_{t:\:c_t\:precede\:c_i}{V_j (c_t)}.$


Очевидно, что

$\sum\limits_{j:c_i\in R_j}\sum\limits_{t:\:c_t\:precede\:c_i}{V_j (c_t)}< \sum\limits_{j:c_i\in R_j}{V(R_j)},$


а значит

$V_{old}-V(c_i)<V_{old}-\sum\limits_{j:c_i\in R_j}\sum\limits_{t:\:c_t\:precede\:c_i}{V_j (c_t)}.$



Последнее неравенство означает, что удаление любого канала $c_i$ как правило приводит к появлению новых цепочек с определенной стоимостью, которые заведомо не принесут конверсий. Таким образом, мы можем оценить потери $Loss(c_i)$ от удаления канала (стоимость всех «усеченных» цепочек), а также экономию $EC(c_i)$ как стоимость всех «неосущественных» переходов, которые имели бы место в случае сохранения канала в цепочках:

$Loss(c_i)=\sum\limits_{j:c_i\in R_j}\sum\limits_{t:\:c_t\:precede\:c_i}{V_j (c_t)},$


$EC(c_i )=\sum\limits_{j:c_i\in R_j}{V(R_j)}-Loss(c_i).$


Теперь, после того, как мы научились оценивать изменение расходов после удаления канала $c_i$, мы можем оценить новую стоимость конверсии, которая бы имела место в случае отсутствия канала:

$ CPA_{new}=\frac{V_{new}}{CV_{new}}=\frac{V_{old}-\sum\limits_{j:c_i\in R_j}\sum\limits_{t:\:c_t\:precede\:c_i}{V_j (c_t)}}{X*(1-I(c_i))} $


Если положить, что до удаления канала мы имели прежнюю стоимость конверсии:

$CPA_{old}=\frac{V_{old}}{X}$

и целью удаления канала стоит снижение стоимости конверсии, то решающее правило может быть следующим:

$CPA_{new}-CPA_{old}<0.$


То есть если удаление канала приводит к снижению стоимости конверсии (при разумном снижении их количества), то его можно исключить из цепочек и перестать тратить на него бюджет.

Кроме того, можно оценить стоимость «недополученных конверсий» при удалении канала:

$CPA_{loss}=\frac{V_{old}-V_{new}}{X*I(c_i)},$

поэтому вместо правила $CPA_{new}-CPA_{old}<0$ можно воспользоваться другим: если выполняется соотношение

$CPA_{loss}>CPA_{old},$

то удаление канала $c_i$ приведет к снижению общей стоимости конверсии на сайте.

Теперь приступим к описанию основной модели, требуемой для расчета вероятности конверсии канала.

Описание модели


Прежде чем мы приступим к описанию многоканальной модели атрибуции, нам бы хотелось сослаться на замечательные статьи Сергея Брыля, и вторую статью, в которых автор использовал красоту и функциональность марковских цепей для описания многоканальной атрибуции. В рамках данной статьи мы более подробно описали основные моменты, связанные с расчетом вероятности конверсии в рамках марковских процессов, а также предложили эффективный метод вычисления вероятности конверсии – на основании стохастических матриц.

Мы предложим две альтернативных интерпретации многоканальной модели атрибуции: графовую и матричную. Первая позволит наглядно описать модель, в то время как вторая позволяет эффективно вычислять требуемые характеристики. Мы покажем, что оба описания на самом деле представляют один и тот же случайный процесс, который называется марковским, а соответствующая процессу модель – марковской цепью.

Графовая модель


Граф — абстрактный математический объект, представляющий собой множество вершин графа и набор рёбер, то есть соединений между парами вершин. Например, за множество вершин можно взять множество аэропортов, обслуживаемых некоторой авиакомпанией, а за множество рёбер взять регулярные рейсы этой авиакомпании между городами.

Граф называется ориентированным, если каждое из его ребер имеет направление, т. е. по сути представляет из себя вектор: для ребра точно указано, из какой вершины оно исходит, и в какой заканчивается.

Граф называется взвешенным, если каждому его ребру приписано некоторое числовое значение, называемое весом. Типичным примером взвешенного ориентированного графа является сеть автомобильных дорог между городами (вершинами графа), где под весом ребра (дороги) мы понимаем ее протяженность.

Для того, чтобы представить множество цепочек в виде графа, нам необходимо зафиксировать два множества: множество вершин $V$ и множество связей $E$ между ними. В роли вершин будут выступать маркетинговые каналы а так же два дополнительных события:

$ V=\{c_1,\: c_2,\: ...,\: c_k,\:CV,\:N\}. $


В качестве $E$ будем выбирать пары соединенных между собой элементов из $V$. Для рассмотренных выше элементарных цепочек имеем:

$ V=\{c_1,\:c_2,\:c_3,\:CV,\:N\},\\ E=\{(c_1,N),\:(c_1,c_2),\:(c_2,N),\:(c_1,CV),\:(c_1,c_2),\:...,\:(c_3,N)\}. $



Ввиду того, что во множестве $E$ могут встречаться совпадающие элементы, полученный граф может иметь кратные (дублированные) ребра.



Как видно, даже для небольшого числа сессий такое графическое представление является достаточно громоздким, что затрудняет анализ. Некоторого упрощения можно добиться, если заменить дублированные ребра одним ребром, взяв за вес количество дублей. Тогда исходный граф преобразуется в ориентированный взвешенный граф:


Данный граф уже более пригоден для анализа. Наша следующая цель – это преобразование веса ребра к вероятностной нотации. Заменим вес ребра, соединяющий две вершины, вероятностью перехода из одной вершины в другую.

В частности, рассмотрим вершину $c_1$. Из нее достижимы следующие вершины графа: $c_2,\:CV,\:N$. Всего из вершины $c_1$ было зафиксировано $1+11+2=14$ переходов, причем $11$ из них было в $c_2$, $2$ – в $N$ и одно в $CV$. Тогда если обозначить $P(c_1,c_2),\:P(c_1,N),\:P(c_1,CV)$ – вероятности перейти из $c_1$ в $c_2,\:CV,\:N$ соответственно, то:

$P(c_1,c_2)=\frac{11}{14},\: P(c_1,N)=\frac{2}{14}=\frac17,\: P(c_1,CV)=\frac{1}{14}.$


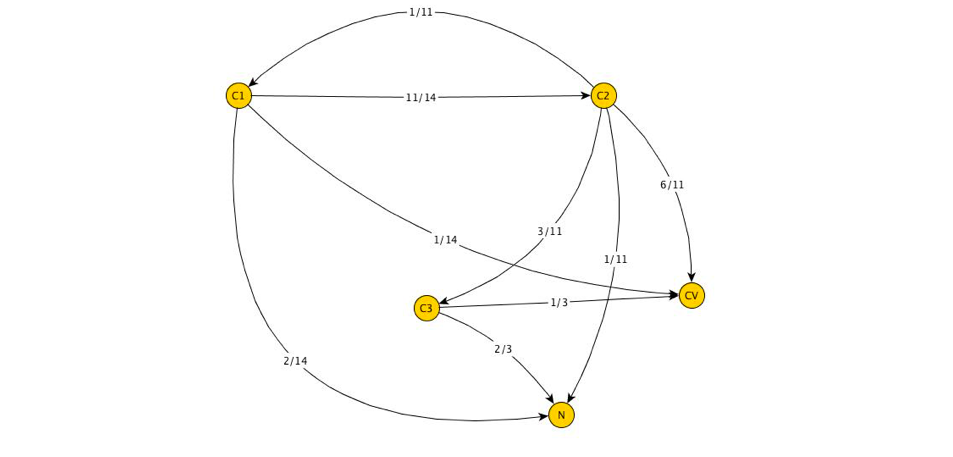
Легко заменить, что $P(c_1,CV)$ — это вероятность конверсии источника $c_1$ в классической модели $LCM.$ Становится очевидно, что модель $LCM$ не учитывает большой объем статистических данных, которые мы можем собрать, анализируя пользовательские сессии. Если произвести расчеты для всех оставшихся вершин, то наш граф будет преобразован к виду:



На основании данной модели можно рассчитать полную вероятность конверсии для определенного канала. Для расчета используется следующая рекурсивная формула:

$ P_{full}(c_i,CV)=\sum\limits_{c_j:c_i\rightarrow c_j}{P(c_i,c_j)P_{full}(c_j,CV)} $


Смысл этой формулы в том, что для того, чтобы рассчитать полную вероятность конверсии некоторой вершины, требуется выбрать все вершины, достижимые из данной, затем рассчитать вероятности перехода в эти вершины из исходной, а затем для каждой достижимой вершины снова рассчитать полную вероятность конверсии. Данная формула тут же дает полную вероятность конверсии, если граф является однонаправленным, т. е. если есть ребро, соединяющее вершины $c_i$ и $c_j$, но отсутствует ребро, которое соединяет $c_j$ c $c_i$. В противном случае указанная выше формула задает систему линейных уравнений, количество неизвестных в которой равно количеству «возвратных» ребер в графе.

Например, рассчитаем полную вероятность конверсии $P_{full}(c_1,CV)$ для источника $c_1$.

Так как $c_1$ связан с $c_2,\:CV,\:N$, но вероятность перейти из $N$ в $CV$ равна нулю, а вероятность перейти из $CV$ в $CV$ равна 1, то:

$ P_{full}(c_1,CV)=P(c_1,c_2)*P_{full}(c_2,CV)+P(c_1,CV)*1=\frac{11}{14}*P_{full} (c_2,CV)+\frac{1}{14}.$


В свою очередь из $c_2$ можно вернуться в $c_1$ или же перейти в $c_3,\:CV,\:N$, а значит:

$ P_{full}(c_2,CV)=P(c_2,c_1)*P_{full}(c_1,CV)+P(c_2,c_3)*P_{full} (c_3,CV)+ P(c_2,CV)*1, \\ P_{full}(c_2,CV)=\frac{1}{11}*P_{full}(c_1,CV)+\frac{3}{11}*P_{full}(c_3,CV)+\frac{6}{11}, $


тогда

$ P_{full}(c_1,CV)=\frac{11}{14}*\Bigl(\frac{1}{11}*P_{full}(c_1,CV)+\frac{3}{11}*P_{full} (c_3,CV)+\frac{6}{11}\Bigr)+\frac{1}{14}. $


Для удобства обозначим $P_{full}(c_1,CV)=x$, тогда получим следующее линейное уравнение:

$ х=\frac{11}{14}*\Bigl(\frac{1}{11}*x+\frac{3}{11}*P_{full}(c_3,CV)+\frac{6}{11}\Bigr)+\frac{1}{14}. $


Теперь рассчитаем $P_{full}(c_3,CV)$. Из источника $c_3$ можно перейти только в $CV$ или $N$. Тогда

$ P_{full}(c_3,CV)=\frac{1}{3}. $


Окончательно имеем следующее уравнение:

$ x=\frac{11}{14}*\Bigl(\frac{1}{11}*x+\frac{3}{11}*\frac{1}{3}+\frac{6}{11}\Bigr)+\frac{1}{14}. $


Откуда

$ x= P_{full}(c_1,CV)=\frac{8}{13}=0.6154. $

.
Основным достоинством указанной выше модели является ее наглядность, в то время к очевидным недостаткам (что видно даже на простом примере) следует отнести высокую вычислительную сложность для случая большого числа источников трафика. Более того, если в качестве источников использовать различные ключевые слова, то объем вычислений увеличивается на порядки, что сделает все последующие расчеты нереализуемыми. Помимо этого, если допустить возможность переходов в графе вида: $...\rightarrow c_i\rightarrow c_i\rightarrow ... $(то есть разрешить петли), то система уравнений становится нелинейной, что заметно усложняет нахождение требуемых вероятностей. В следующем разделе мы перейдем к рассмотрению матричной модели и покажем эффективные методы вычисления формул полной вероятности.

Матричная модель


В предыдущей главе мы рассмотрели графовую модель мультиканальной атрибуции. Для того, чтобы преобразовать ее к более удобному для вычислений виду, вновь рассмотрим набор из $k$ каналов $c_1,c_2,...c_k$ и двух дополнительных «псевдоканалов» $CV$, $N$. Напомню, что в графовой модели они играли роль вершин.

По наблюдаемым последовательностям, составленным для каждого из пользователей, мы можем без труда рассчитать вероятности перехода (иначе говоря, условные вероятности) $P(c_i,c_j),\:P(c_i,CV),\:P(c_i,N)$. Как уже было отмечено ранее, будем считать, что $P(N,c_i)=P(CV,c_i)=0$ и $P(N,N)=P(CV,CV)=1$. Тогда можно составить квадратную матрицу размера $(k+2)\times(k+2)$, элементами которой будут условные вероятности $P(c_i,c_j),\:P(c_i,CV),\:P(c_i,N),\:P(N,c_i),\:P(CV,c_i):$
и $P(N,N),\:P(CV,CV)$:

$ H=\begin{pmatrix} P(c_1,c_1)& P(c_1,c_2)& …& P(c_1,c_k)& P(c_1,CV) & P(c_1,N) \\ P(c_2,c_1)& P(c_2,c_2)& …& P(c_2,c_k)& P(c_2,CV) & P(c_2,N) \\ …&…&…&…&…&… \\ P(c_k,c_1) & P(c_k,c_2) & … & P(c_k,c_k) & P(c_k,CV) & P(c_k,N) \\ 0&0&…&0&1&0 \\ 0&0&…&0&0&1 \end{pmatrix} $



В частности, для рассматриваемого выше примера мы получим:

$ H=\begin{pmatrix} 0&\frac{11}{14}&0&\frac{1}{14}&\frac{2}{14}\\ \frac{1}{11}&0&\frac{3}{11}&\frac{6}{11}&\frac{1}{11}\\ 0&0&0&\frac13&\frac23\\ 0&0&0&1&0\\ 0&0&0&0&1 \end{pmatrix} $



Легко заметить, что для любой $i$ строки матрицы $H$ справедливо:

$ \sum\limits_{j=1}^k{P(c_i,c_j)}+P(c_i,CV)+P(c_i,N)=1. $


Матрица, для которой выполнено данное условие, называется стохастической. Известно, что произвольная стохастическая матрица определяет некоторый случайный процесс, называемый марковским. Дадим такому процессу более формальное (хотя и не строгое с математической точки зрения) определение.

Марковским процессом называется такой случайный процесс с некоторым числом состояний, что вероятность перехода в следующее состояние зависит только от того текущего состояния, в котором находится система.

Таким образом, рассматриваемый нами процесс переходов между различными маркетинговыми каналами можно считать марковским процессом, определяемым матрицей переходных вероятностей $H$. Определенная таким образом модель позволяет ответить на ряд важных вопросов, в частности:

  • Какова вероятность перейти из состояния $c_i$ в состояние $c_j$ за $t$ шагов?
  • Как будет выглядеть распределение вероятности нахождения в каждом из каналов через $t$ шагов?

В нашей прикладной задаче оценки вероятности конверсии каждого из каналов, нам требуется ответить на частный случай первого вопроса:

Какова полная вероятность перейти из состояния (канала) $c_i$ в $CV$?

Марковская теория случайных процессов позволяет дать очень простой ответ на этот вопрос (в случае, если из состояний $CV$ и $N$ невозможны переходы ни в какие другие состояния): для расчета данной вероятности необходимо возвести матрицу в бесконечную степень и взять значение, стоящее на позиции $(i,k+1)$:

$ P_{full}(c_i,CV)=\lim_{t\rightarrow \infty}H^t (i,k+1). $


Можно строго доказать, что для случая, когда из состояний $CV$ и $N$ невозможны переходы ни в какое другое состояние, этот предел существует. Конечно, на практике мы не можем оперировать с «бесконечной» степенью матрицы. Однако вместо «бесконечности» как правило достаточно взять достаточно большую степень двойки. Удобство возведения матрицы в степень $2^t$ заключается в том, что требуется произвести ровно умножений матрицы $H$ на себя.

В самом деле, пусть, например, $t=8$. Тогда для вычисления $H^{2^8}=H^{256}$ достаточно вычислить:

$H*H=H^2,\\ H^2*H^2=H^4,\\ H^4*H^4=H^8,\\ H^8*H^8=H^{16},\\ H^{16}*H^{16}=H^{32},\\ H^{32}*H^{32}=H^{64},\\ H^{64}*H^{64}=H^{128},\\ H^{128}*H^{128}=H^{256}. $


Покажем на нашем примере скорость «сходимости» предела к нужной нам вероятности:



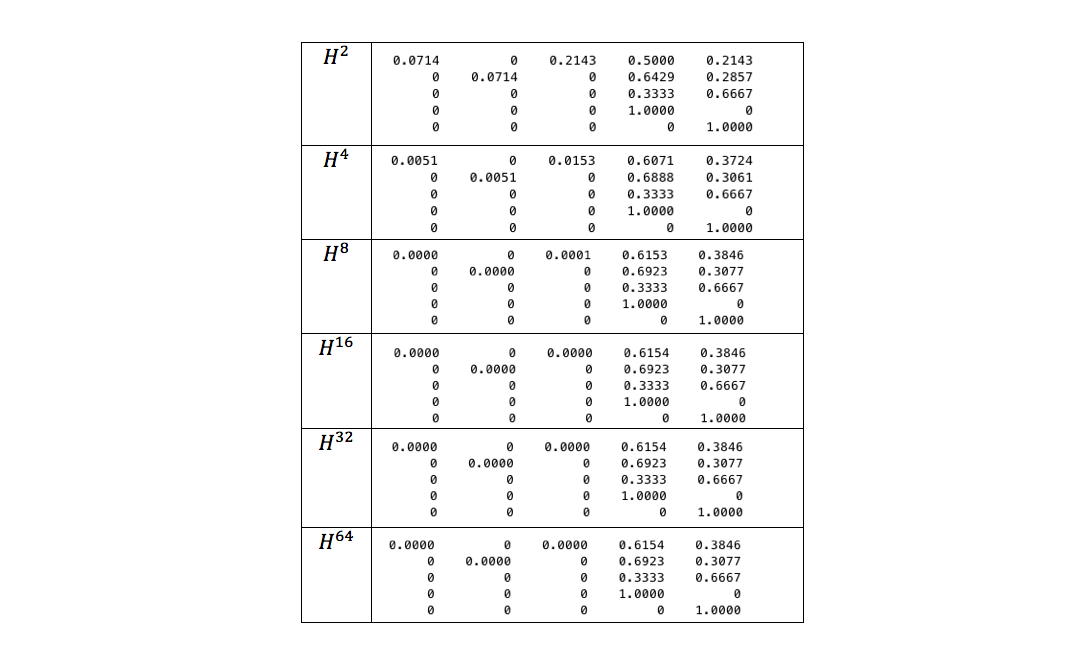
Как видно из таблицы, уже для $H^8$ рассчитанная вероятность $P_{full}(c_1,CV)$ отличается от точного значения, которое мы ранее получили на основе графовой модели, в 4 знаке после запятой. Значения вероятностей, посчитанные для $H^{16}$, $H^{32}$, $H^{64}$ и вовсе совпадают. Таким образом, в данном случае достаточно было ограничиться вычислением $H^8$, что требует всего $3$ матричных умножения. Таким образом, скорость сходимости предела к требуемой вероятности достаточно высока, что делает данную модель эффективной в практических приложениях.

От оценки каналов к оптимизации


Построенная аналитическая модель позволяет решить 3 основные задачи:

  • Оценить влияние канала на конверсию на сайте
  • Оценить взаимное влияние каналов друг на друга
  • Оценить вероятность того, что использование канала приведет к конверсии на сайте

При проектировании оптимизатора конверсий, который позволяет управлять ставками в контекстной рекламе на основе их эффективности так, чтобы достигать требуемых $KPI$ (ключевых показателей эффективности), требуется оценивать коэффициент конверсии $CR$ для каждой ключевой фразы. Как нами отмечалось, выбор той или иной модели атрибуции конверсий напрямую влияет на расчет коэффициента конверсии не только на уровне рекламного канала, но и на уровне ключевой фразы. Традиционно оптимизаторы работают с моделью $LCM$ или ее модификациями. Ранее мы показали ограниченную способность $LCM$ предсказывать коэффициент конверсии (как правило она занижает его, так как учитывает только прямую связь кейворд конверсия, не анализируя промежуточные переходы).

Представленная модель атрибуции конверсий избавлена от этих недостатков, хотя для вычисления вероятностей требует значительно больше вычислительных ресурсов. Гибкость описанного подхода заключается еще и в том, что в качестве «канала» мы можем использовать любой неотъемлемый атрибут сессии.

В частности, рассмотрим параметр $URL$, который не использовался нами ранее в расчетах. $URL$ содержит информацию о той странице на сайте, на которую переходит пользователь в начале сессии. Если на ассоциированном с сайтом рекламном аккаунте все объявления размечены $UTM-$метками, то мы можем значительно углубить нашу аналитику.

$UTM$ метки – это параметры (переменные) содержащие дополнительные данные, которые добавляются к $URL$ целевой (посадочной) страницы и позволяют передать в системы веб-аналитики дополнительную информацию о характеристиках трафика. Рассмотрим типичный пример $UTM$ метки, например в формате, принятом в компании $Calltouch$:
site.ru/?utm_source=YD&utm_medium=cpc&utm_content=kvartiry_ceny&utm_campaign=YD_KVARTIRY_POISK_MSK&calltouch_tm=yd_c:{campaign_id}_gb:{gbid}_ad:{ad_id}_ph:{phrase_id}_st:{source_type}_pt:{position_type}_p:{position}_s:{source}_dt:{device_type}_reg:{region_id}_ret:{retargeting_id}_apt:{addphrasestext}

На основе динамических параметров, которые содержатся в фигурных скобках, мы можем, в частности, отследить «путь» клика на рекламное объявление с точностью до ключевой фразы, которая инициировала показ рекламного объявления, на которое кликнул пользователь. Мы можем выбрать любой «разумный» динамический параметр (или их связку) в качестве канала. В частности, если выбрать в качестве канала параметр $\{phrase_{id}\}$, то мы можем отследить цепочки переходов пользователя на сайт по разным ключевым словам. Если повторить все рассуждения для такого типа каналов, то модель позволит рассчитать полную вероятность конверсии для каждой ключевой фразы.

Полученный таким образом массив коэффициентов конверсии можно использовать в качестве входных данных для оптимизатора конверсий.

Заключение


В работе дан обзор используемых в настоящий момент классических моделей атрибуции конверсий. Кроме того описана модель мультиканальной атрибуции, основанная на марковских процессах (цепях), которая позволяет комплексно оценить как вероятность конверсии для каждого рекламного канала, так и рассчитать влияние канала на конверсию на сайте. Продемонстированы подходы, позволяющие адаптировать построенную модель для оптимизации ставок в контекстной рекламе.
Теги:
Хабы:
Всего голосов 2: ↑2 и ↓0+2
Комментарии4
1
Карма
0
Рейтинг
@CalltouchForever

Пользователь

Отправить сообщение

Публикации

Ближайшие события

Ваш аккаунт

Разделы

Информация

Услуги

Техническая поддержка
© 2006–2025, Habr