AndrewSu 18 мар 2019 в 22:25

Задача N тел или как взорвать галактику не выходя из кухни

34 мин

48K

GPGPU*Алгоритмы*Математика*Параллельное программирование*Физика

Не так давно я прочёл фантастический роман «Задача трёх тел» Лю Цысиня. В нём у одних инопланетян была проблема — они не умели, с достаточной для них точностью, вычислять траекторию своей родной планеты. В отличии от нас, они жили в системе из трёх звёзд, и от их взаимного расположения сильно зависела «погода» на планете — от испепеляющей жары до леденящего мороза. И я решил проверить, можем ли мы решать подобные задачи.

Физика явления

Для понимания задачи необходимо разобраться с физикой явления. В рамках классической теории сила притяжения двух тел определяется законом Ньютона:

$\vec{F}(\vec{r}_1, \vec{r}_2)=-G m_1 m_2 \frac{\vec{r}_1 - \vec{r}_2}{|\vec{r}_1 - \vec{r}_2|^3},$

где $\vec{r}_1, \vec{r}_2$ — положение тел в пространстве, $inline$ — массы тел, $inline$ — гравитационная постоянная.
В системе из $inline$ тел на каждое из них будет действовать сила притяжения от остальных, что выражается уравнением:

$\vec{F}_n=-G \sum_{k \neq n} m_n m_k \frac{\vec{r}_n - \vec{r}_k}{|\vec{r}_n - \vec{r}_k|^3}.$

Воспользовавшись вторым законом Ньютона запишем ускорение для каждой частицы:

$\vec{a}_n = \vec{F}_n/m_n = -G \sum_{k \neq n} m_k \frac{\vec{r}_n - \vec{r}_k}{|\vec{r}_n - \vec{r}_k|^3}.$

Вспоминая, что ускорение — это вторая производная координаты по времени, получим дифференциальное уравнение второго порядка в частных производных, которое необходимо решить для получения траектории каждого тела:

$\frac{\partial^2 \vec{r}_n }{\partial t^2} = f_n =-G \sum_{k \neq n} m_k \frac{\vec{r}_n - \vec{r}_k}{|\vec{r}_n - \vec{r}_k|^3}.$

Здесь важно заметить, что сложность вычисления функции $inline$ равна $inline$ и сильно возрастает с увеличением количества взаимодействующих тел.

Математика

Первым и простейшим методом решения дифференциальных уравнений является метод Эйлера, который предназначен для решения уравнений вида:

$\frac{dy}{dx}=f(x,y).$

При переходе в дискретную область получим:

$y_{i}=y_{i-1}+h f(x_{i-1},y_{i-1}),\quad i=1,2,3,\dots ,m,$

где $inline$ — шаг интегрирования, а $inline$ — число шагов интегрирования. Таким образом, ести нам необходимо произвести вычисление положения тел на момент времени $inline$ , то нам следует сделать $inline$ шагов интегрирования. Тут видна первая проблема — если $inline$ велико, то нам нужно сделать большое количество шагов интегрирования.

Для применения метода Эйлера к нашей задаче её следует свести к системе первого порядка. Для этого введём дополнительную переменную — скорость частицы:

$\frac{\partial \vec{v}_n }{\partial t} = f_n,\\ \frac{\partial \vec{r}_n }{\partial t} = \vec{v}_n.$

Второй проблемой в решении систем дифференциальных уравнений является точность решения и её контроль. Точность можно повышать двумя способами: уменьшением шага интегрирования и выбором метода с более высоким порядком точности. Оба способа ведут к увеличению вычислительной сложности, но разными путями. Например, можно использовать классический метод Рунге-Кутты четвертого порядка, он требует четырёх вычислений функции $inline$ на каждом шаге, но имеет порядок точности $inline$ (для сравнения, метод Эйлера имеет порядок точности $inline$ и требует одного вычисления $inline$ ). Контроль точности решения также можно осуществлять несколькими способами: сравнить с аналитическим решением, решить разными методами или с разным шагом и сравнить результаты, контролировать сторонние параметры и ограничения, которым должно соответствовать решение.
Также, у каждого из этих методов есть свои недостатки. Аналитические решения могут отсутствовать, или, даже в большинстве случаев, и вовсе отсутствуют. Например, для нашей задачи $inline$ тел аналитическое решение есть только при $inline$ , но даже этого достаточно для тестирования точности методов. Решение задачи двумя методами или с разным шагом увеличивает время вычислений, но этот подход возможно применять практически для любой задачи. Ограничения есть не у каждой задачи, но для нашей они есть: на каждом шаге интегрирования мы можем контролировать выполнение законов сохранения. Этот подход тоже увеличивает сложность вычисления, но здесь есть из чего выбирать, вычисление суммы импульсов или моментов импульса всех частиц имеет сложность порядка $inline$ , в то время как вычисление полной энергии системы имеет сложность порядка $inline$

Заметка про вычисление полной энергии

В нашем случае полная энергия системы состоит из двух частей — кинетической и потенциальной энергии. Кинетическая энергия состоит из суммы кинетических энергий всех тел. Для вычисления же потенциальной энергии нужно сложить потенциальные энергии каждой частицы в гравитационном поле остальных частиц, таким образом нам нужно сложить $inline$ слагаемых. Сложность в том, что все слагаемые имеют сильно разный порядок, и даже при вычислениях с двойной точностью не удаётся вычислить это значение с точностью, достаточной для сравнения на разных шагах. Для преодоления этой проблемы пришлось применить суммирование по алгоритму Кэхэна.

Рис 1. Пример эллиптической траектории.

Рассмотрим простой случай движения спутника по эллиптической орбите вокруг Земли. При приближении спутника к Земле его скорость увеличивается, а при удалении от Земли уменьшается, соответственно, напрашивается возможность уменьшать шаг интегрирования по времени на зелёном участке орбиты, и увеличивать на красном и синем без изменения точности решения. Попробуем сравнить более детально.

Таблица 1. Исследуемые методы решения дифференциальных уравнений

Обозначене	Порядок	Описание
adams	1-5	Метод Адамса-Башфорта
euler	1	Метод Эйлера
rk4	4	Классический метод Рунге-Кутты
rkck	5	Метод Каша-Карпа
rkdp	5	Метод Дормана-Принса
rkdverk	6	Метод Вернера 1) p. 181
rkf	7	Метод Фельберга 1) p. 180
rkgl	6	Неявный метод Гаусса-Лежандра
rklc	4	Неявный метод Лобатто
trapeze	2	Метод трапеций

Для выбора наилучшего метода для нашей задачи произведём сравнение нескольких известных методов. Для этого смоделируем столкновение двух систем тел $inline$ и измерим относительное изменение полной энергии, импульса и его момента в конце моделирования (максимальное время моделирования $T_{max} = 2.5$ ). При этом мы будем варьировать шаг и параметры методов интегрирования и замерять количество вызовов функции $inline$ , соответственно, те методы, которые при меньшем числе вызовов приведут к меньшим потерям, будем считать более приемлимыми.


a)	b)
Рис 2. Относительное изменение энергии a), импульса b), в конце моделирования системы $inline$ тел различными методами в зависимости от количества вычислений функции $inline$ с двойной точностью (double)

Из графиков рисунке 2 видно, что наилучшее соотношение количества вычисления функции $inline$ и относительного изменения энергии системы тел у методов Адамса пятого порядка и Дормана-Принса. Также видно, что для всех методов с ростом числа вычисления $inline$ увеличивается относительное изменение импульса системы. Для относительного изменения энергии это также заметно, но только для нескольких методов, которые смогли достичь порога $dE/E_0 < 10^{-12}$ . Этот эффект можно связать уже не с погрешностью методов, а с погрешностью вычислений, и дальнейшее увеличение точности возможно только совместно с увеличением точности вычислений с плавающей точкой.


a)	b)
Рис 3. Относительное изменение энергии a), импульса b), в конце моделирования системы $inline$ тел различными методами в зависимости от количества вычислений функции $inline$ с четверной точностью (__float128)

Из рисунков 3a и 3b видно, что применение вычислений с четверной точностью позволяет снизить относительные потери энергии вплоть до $10^{-23}$ , но нужно понимать, что время вычислений по сравнению с двойной точностью увеличивается на два порядка. Как и в случае с вычислениями с двойной точностью наилучшим соотношением точности и количества вычислений функции $inline$ обладают методы Адамса пятого порядка и Дормана-Принса.

Методы Дормана-Принса и Вернера относятся к классу вложенных методов и позволяют одновременно вычислить два решения с высоким и низким порядком точности (для метода Дормана-Принса порядки 5 и 4, а для метода Вернера порядки 6 и 5). Если эти два решения сильно отличаются, то мы можем разбить текущий шаг интегрирования на более мелкие. Что позволяет нам динамически изменять шаг интегрирования и уменьшать его только на тех участках, где это требуется.

Сравним методы Дормана-Принса, Вернера и Адамса пятого порядка более детально, на более длительном интервале моделирования нашей системы ( $T_{max} = 300$ ).

a) Относительное изменение энергии, импульса и его момента в процессе моделирования

b) Количество вычислений функции $inline$ на интервале моделирования $\Delta T=0.3$

Рис 4. Зависимости относительного изменения физических параметров системы и количества вычислений функции $inline$ от времени моделирования методом Дормана-Принса с переменным шагом $h=10^{-5}\dots 10^{-9}$

a) Относительное изменение энергии, импульса и его момента в процессе моделирования

b) Количество вычислений функции $inline$ на интервале моделирования $\Delta T=0.3$

Рис 5. Зависимости относительного изменения физических параметров системы и количества вычислений функции $inline$ от времени моделирования методом Вернера с переменным шагом $h=10^{-5}\dots 10^{-9}$

Рис 6. Относительное изменение энергии, импульса и его момента в процессе моделирования методом Адамса-Башфорта пятого порядка с шагом $h=10^{-6}$

Рис 7. Зависимости количества вычислений функции $inline$ для методов Адамса пятого порядка, Дормана-Принса и Вернера от времени моделирования

Видно, что на начальном этапе эволюции нашей системы ( $inline$ ) все три метода показывают схожие характеристики, но на более поздних этапах в системе происходят некие события, в результате которых резко подскакивают ошибки в основных параметрах системы (полной энергии, импульса и его момента). Но методы Дормана-Принса и Вернера справляется с этими изменениями существенно лучше за счёт возможности уменьшать шаг интегрирования на «сложных» участках, в результате чего возрастает число вычислений функции $inline$ , что видно на рисунках 4b и 5b, но общее число вычислений $inline$ у вложенных методов меньше, чем у метода Адамса-Башфорта, что видно на рисунке 7.

Интересно, что происходило с системой в эти моменты

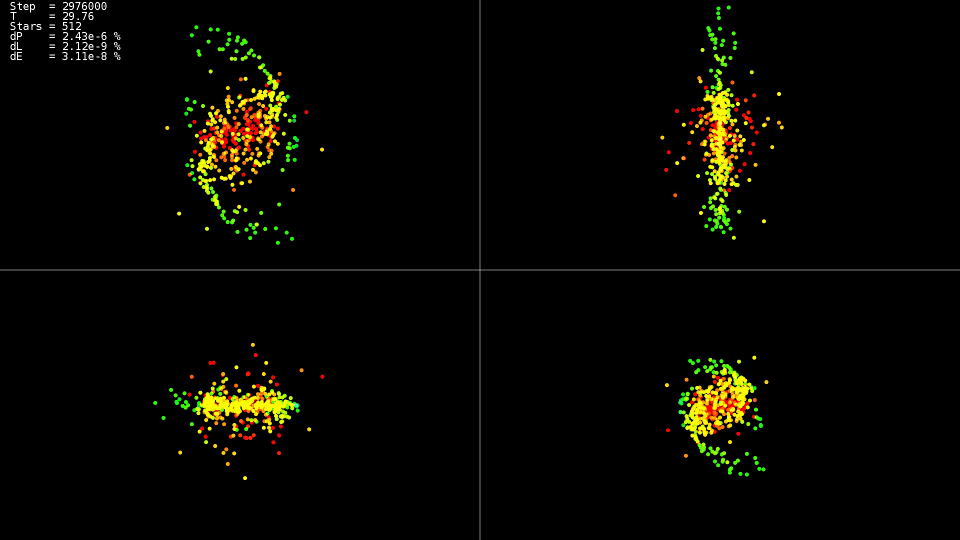
Видео 1. Моделирование системы из 512 тел. Метод Дормана-Принса. Динамический шаг $h=10^{-5}\dots 10^{-9}$

Видео демонстрирует, что до момента времени $inline$ движение относительно спокойное, а после происходит столкновение центров «галактик», которое приводит к резкому изменению траекторий и сильному увеличению скоростей некоторых частиц. При этом для сохранения точности решения необходимо уменьшать шаг интегрирования. Вложенные методы могут сделать это автоматически, на графиках видно, что на некоторых участках эволюции системы шаг интегрирования был уменьшнен почти на два порядка с $10^{-5}$ до $h=10^{-7}$ . При использовании метода Адамса и такого шага на всём интервале эволюции системы мы не дождались бы решения.

Итог

Для решения лучше использовать вложеные методы, которые позволяют динамически контролировать шаг интегрирования, и уменьшать его только на «сложных» участках траектории.

Не стоит гнаться за методами самого высокого порядка. Даже при использовании типа данных 'double' они не достигают своих потенциальных возможностей, использование же типов данных с большей точностью сильно увеличивает время решения задачи.

CPU реализация

Теперь, когда выбор метода решения уравнений определён, попробуем разобраться с вычислением силы взаимодействия для каждой частицы. Получим двойной цикл по всем частицам:

Код реализации 'simple'

for(size_t body1 = 0; body1 < count; ++body1)
{
    const nbvertex_t    v1(rx[ body1 ], ry[ body1 ], rz[ body1 ]);
    nbvertex_t          total_force;
    for(size_t body2 = 0; body2 != count; ++body2)
    {
        if(body1 == body2)
        {
            continue;
        }
        const nbvertex_t    v2(rx[ body2 ], ry[ body2 ], rz[ body2 ]);
        const nbvertex_t    force(m_data->force(v1, v2, mass[body1], mass[body2]));
        total_force += force;
    }
    frx[body1] = vx[body1];
    fry[body1] = vy[body1];
    frz[body1] = vz[body1];
    fvx[body1] = total_force.x / mass[body1];
    fvy[body1] = total_force.y / mass[body1];
    fvz[body1] = total_force.z / mass[body1];
}

Силы притяжения для каждого тела вычисляются независимо, и, для задействования всех ядер процессора, достаточно перед первым циклом написать директиву OpenMP:

Кусочек кода из реализации 'openmp'

#pragma omp parallel for
for(size_t body1 = 0; body1 < count; ++body1)

Т.к. каждое тело взаимодействует с каждым, то для уменьшения количества взаимодействий процессора с ОЗУ и улучшения использования кэша у нас есть возможность загружать в кэш часть данных и использовать их многократно:

Код реализации 'openmp+block'

#pragma omp parallel for
for(size_t n1 = 0; n1 < count; n1 += BLOCK_SIZE)
{
    nbcoord_t            x1[BLOCK_SIZE];
    nbcoord_t            y1[BLOCK_SIZE];
    nbcoord_t            z1[BLOCK_SIZE];
    nbcoord_t            m1[BLOCK_SIZE];
    nbvertex_t           total_force[BLOCK_SIZE];

    for(size_t b1 = 0; b1 != BLOCK_SIZE; ++b1)
    {
        size_t local_n1 = b1 + n1;

        x1[b1] = rx[local_n1];
        y1[b1] = ry[local_n1];
        z1[b1] = rz[local_n1];
        m1[b1] = mass[local_n1];
    }
    for(size_t n2 = 0; n2 < count; n2 += BLOCK_SIZE)
    {
        nbcoord_t            x2[BLOCK_SIZE];
        nbcoord_t            y2[BLOCK_SIZE];
        nbcoord_t            z2[BLOCK_SIZE];
        nbcoord_t            m2[BLOCK_SIZE];

        for(size_t b2 = 0; b2 != BLOCK_SIZE; ++b2)
        {
            size_t local_n2 = b2 + n2;

            x2[b2] = rx[local_n2];
            y2[b2] = ry[local_n2];
            z2[b2] = rz[local_n2];
            m2[b2] = mass[n2 + b2];
        }

        for(size_t b1 = 0; b1 != BLOCK_SIZE; ++b1)
        {
            const nbvertex_t    v1(x1[ b1 ], y1[ b1 ], z1[ b1 ]);
            for(size_t b2 = 0; b2 != BLOCK_SIZE; ++b2)
            {
                const nbvertex_t    v2(x2[ b2 ], y2[ b2 ], z2[ b2 ]);
                const nbvertex_t    force(m_data->force(v1, v2, m1[b1], m2[b2]));
                total_force[b1] += force;
            }
        }
    }

    for(size_t b1 = 0; b1 != BLOCK_SIZE; ++b1)
    {
        size_t local_n1 = b1 + n1;
        frx[local_n1] = vx[local_n1];
        fry[local_n1] = vy[local_n1];
        frz[local_n1] = vz[local_n1];
        fvx[local_n1] = total_force[b1].x / m1[b1];
        fvy[local_n1] = total_force[b1].y / m1[b1];
        fvz[local_n1] = total_force[b1].z / m1[b1];
    }
}

Дальнейшая оптимизация заключается в вынесении содержимого функции вычисления силы в основной цикл и исключении деления и умножения на массу тела m1[b1]. Кроме того, что мы немного сократили вычисления, компилятор на таком развёрнутом цикле сможет применить векторные инструкции процессора SSE и AVX.

Код реализации 'openmp+block+optimization'

#pragma omp parallel for
for(size_t n1 = 0; n1 < count; n1 += BLOCK_SIZE)
{
    nbcoord_t            x1[BLOCK_SIZE];
    nbcoord_t            y1[BLOCK_SIZE];
    nbcoord_t            z1[BLOCK_SIZE];
    nbcoord_t            total_force_x[BLOCK_SIZE];
    nbcoord_t            total_force_y[BLOCK_SIZE];
    nbcoord_t            total_force_z[BLOCK_SIZE];

    for(size_t b1 = 0; b1 != BLOCK_SIZE; ++b1)
    {
        size_t local_n1 = b1 + n1;

        x1[b1] = rx[local_n1];
        y1[b1] = ry[local_n1];
        z1[b1] = rz[local_n1];
        total_force_x[b1] = 0;
        total_force_y[b1] = 0;
        total_force_z[b1] = 0;
    }
    for(size_t n2 = 0; n2 < count; n2 += BLOCK_SIZE)
    {
        nbcoord_t            x2[BLOCK_SIZE];
        nbcoord_t            y2[BLOCK_SIZE];
        nbcoord_t            z2[BLOCK_SIZE];
        nbcoord_t            m2[BLOCK_SIZE];

        for(size_t b2 = 0; b2 != BLOCK_SIZE; ++b2)
        {
            size_t local_n2 = b2 + n2;

            x2[b2] = rx[local_n2];
            y2[b2] = ry[local_n2];
            z2[b2] = rz[local_n2];
            m2[b2] = mass[n2 + b2];
        }

        for(size_t b1 = 0; b1 != BLOCK_SIZE; ++b1)
        {
            for(size_t b2 = 0; b2 != BLOCK_SIZE; ++b2)
            {
                nbcoord_t        dx = x1[b1] - x2[b2];
                nbcoord_t        dy = y1[b1] - y2[b2];
                nbcoord_t        dz = z1[b1] - z2[b2];
                nbcoord_t        r2(dx * dx + dy * dy + dz * dz);
                if(r2 < NBODY_MIN_R)
                {
                    r2 = NBODY_MIN_R;
                }
                nbcoord_t        r = sqrt(r2);
                nbcoord_t        coeff = (m2[b2]) / (r * r2);

                dx *= coeff;
                dy *= coeff;
                dz *= coeff;

                total_force_x[b1] -= dx;
                total_force_y[b1] -= dy;
                total_force_z[b1] -= dz;
            }
        }
    }

    for(size_t b1 = 0; b1 != BLOCK_SIZE; ++b1)
    {
        size_t local_n1 = b1 + n1;
        frx[local_n1] = vx[local_n1];
        fry[local_n1] = vy[local_n1];
        frz[local_n1] = vz[local_n1];
        fvx[local_n1] = total_force_x[b1];
        fvy[local_n1] = total_force_y[b1];
        fvz[local_n1] = total_force_z[b1];
    }
}

Таблица 2. Зависимость времени вычисления (в секундах) функции $inline$ от количества взаимодействующих тел $inline$ для различных CPU реализаций

$inline$	2048	4096	8192	16384	32768
simple	0.0425	0.1651	0.6594	2.65	10.52
openmp	0.0078	0.0260	0.1079	0.417	1.655
openmp+block+optimization	0.0037	0.0128	0.0495	0.194	0.774

Параметры системы:

cистема: Debian 9, Intel Core i7-5820K (6 core)
компилятор: gcc 6.3.0

Хорошо видно, что версия с поддержкой OpenMP ускоряется в шесть раз, ровно по количеству ядер, а оптимизированная версия быстрее ещё немногим более чем в два раза. Так что, при оптимизации не стоит рассчитывать только на параллелизм. Интересно, что при вычислениях в один поток (simple) процессор работал на частоте 3.6 ГГц, в параллельной версии (openmp) сбросил частоту до 3.4 ГГц, а в параллельной и оптимизированной (openmp+block+optimization) сбросил ещё до 3.3 ГГц, но это не помешало ей работать в 13.6 раз быстрее. Также видно, что рост времени вычисления с увеличением размера задачи квадратичен, и дальнейшее увеличение $inline$ делает задачу нерешаемой за разумное время.

GPU реализация

Но возникает желание производить вычисления ещё быстрее. Есть несколько доступных направлений для ускорения: вычисление на GPU, аппроксимация функции $inline$ . Сначала для произведения вычислений на GPU я выбрал технологию OpenCL. Для более удобной работы была использована библиотека CLHPP. Главным достоинством OpenCL является то, что код можно запускать и на процессоре, и на GPU, что упрощает написание и отладку, а также расширяет список железа для запуска. В отладке помогает инструмент Oclgrind, который в рантайме показывает неверные вызовы OpenCL API и проблемы при обращении к памяти.

OpenCL

Для начала работы с OpenCL необходимо получить список доступных платформ. Самые распространённые платформы представляют компании AMD, Intel и NVidia.

Код

std::vector<cl::Platform>     platforms;
cl::Platform::get(&platforms);

Далее, после выбора платформы, нужно выбрать вычислительное устройство, которое эта платформа представляет:

Код

const cl::Platform&     platform(platforms[platform_n]);
std::vector<cl::Device> all_devices;
platform.getDevices(CL_DEVICE_TYPE_ALL, &all_devices);

И в заключение подготовительного этапа нужно создать контекст и очереди в рамках которых будет выделяться память и производиться вычисления. Например, контекст, объединяющий все вычислительные устройства выбранной платформы, создаётся следующим образом:

Код создания контекста и очередей

cl::Context                   context(all_devices);
std::vector<cl::CommandQueue> queues;
for(cl::Device device: all_devices)
    queues.push_back(cl::CommandQueue(context, device));

Для загрузки исходного кода на вычислительное устройство его необходимо скомпилировать, для этого предназначен класс cl::Program.

Код компиляции ядра

std::vector< std::string >   source_data;
cl::Program::Sources         sources;
for(int i = 0; i != files.size(); ++i)
{
    source_data.push_back(load_program(files[i]));//Загружаем из файла
    sources.push_back(std::make_pair(source_data.back().data(),
                                     source_data.back().size()));
}
cl::Program    prog(context, sources);
devices.push_back(all_devices);
prog.build(devices, options);

Для описания параметров функции (ядра), которая выполняется на вычислительном устройстве есть удолный шаблон cl::make_kernel.

Пример объявления ядра вычисления силы взаимодействия

typedef cl::make_kernel< cl_int, cl_int, //Block offset
                         cl::Buffer, //mass
                         cl::Buffer, //y
                         cl::Buffer, //f
                         cl_int, cl_int, //yoff,foff
                         cl_int, cl_int //points_count,stride
                         > ComputeBlock;

Далее все просто: объявляем переменную с типом ядра, передаём в неё скомпилированную программу и имя вычислительного ядра, можем запускать ядро почти как обычную функцию.

Код запуска ядра

ComputeBlock        fcompute(prog, "ComputeBlockLocal");
cl::NDRange         global_range(device_data_size);
cl::NDRange         local_range(block_size);
cl::EnqueueArgs     eargs(ctx.m_queue, global_range, local_range);
fcompute(eargs, ...все остальные аргументы); //Собственно, сам вызов ядра.

Само вычислительное ядро для OpenCL очень похоже на вариант 'openmp+block+optimization' для CPU, только в отличии от CPU версии управление первым циклом происходит при помощи OpenCL (диапазон цикла определяется переменной global_range из кода запуска ядра, а из ядра номер текущей итерации доступен с помощью функции get_global_id(0)). Сначала часть данных о телах загружается с локальную память, затем обрабатывается. Локальная память является общей для всех потоков в группе, поэтому загрузка происходит один раз для группы, а обрабатывается каждым потоком в группе и, т.к. локальная память существенно быстрее глобальной, вычисления происходят много быстрее.

Код ядра

__kernel void ComputeBlockLocal(int offset_n1, int offset_n2,
                                __global const nbcoord_t* mass,
                                __global const nbcoord_t* y,
                                __global nbcoord_t* f, int yoff,
                                int foff, int points_count, int stride)
{
    int        n1 = get_global_id(0) + offset_n1;
    __global const nbcoord_t*    rx = y + yoff;
    __global const nbcoord_t*    ry = rx + stride;
    __global const nbcoord_t*    rz = rx + 2 * stride;
    __global const nbcoord_t*    vx = rx + 3 * stride;
    __global const nbcoord_t*    vy = rx + 4 * stride;
    __global const nbcoord_t*    vz = rx + 5 * stride;

    __global nbcoord_t*    frx = f + foff;
    __global nbcoord_t*    fry = frx + stride;
    __global nbcoord_t*    frz = frx + 2 * stride;
    __global nbcoord_t*    fvx = frx + 3 * stride;
    __global nbcoord_t*    fvy = frx + 4 * stride;
    __global nbcoord_t*    fvz = frx + 5 * stride;

    nbcoord_t    x1 = rx[n1];
    nbcoord_t    y1 = ry[n1];
    nbcoord_t    z1 = rz[n1];

    nbcoord_t    res_x = 0.0;
    nbcoord_t    res_y = 0.0;
    nbcoord_t    res_z = 0.0;

    __local nbcoord_t    x2[NBODY_DATA_BLOCK_SIZE];
    __local nbcoord_t    y2[NBODY_DATA_BLOCK_SIZE];
    __local nbcoord_t    z2[NBODY_DATA_BLOCK_SIZE];
    __local nbcoord_t    m2[NBODY_DATA_BLOCK_SIZE];

    // NB! get_local_size(0) == NBODY_DATA_BLOCK_SIZE
    for(int b2 = 0; b2 < points_count; b2 += NBODY_DATA_BLOCK_SIZE)
    {
        int    n2 = b2 + offset_n2 + get_local_id(0);

        // Copy data block to local memory
        x2[ get_local_id(0) ] = rx[n2];
        y2[ get_local_id(0) ] = ry[n2];
        z2[ get_local_id(0) ] = rz[n2];
        m2[ get_local_id(0) ] = mass[n2];

        // Synchronize local work-items copy operations
        barrier(CLK_LOCAL_MEM_FENCE);

        nbcoord_t    local_res_x = 0.0;
        nbcoord_t    local_res_y = 0.0;
        nbcoord_t    local_res_z = 0.0;

        for(int local_n2 = 0; local_n2 != NBODY_DATA_BLOCK_SIZE; ++local_n2)
        {
            nbcoord_t    dx = x1 - x2[local_n2];
            nbcoord_t    dy = y1 - y2[local_n2];
            nbcoord_t    dz = z1 - z2[local_n2];
            nbcoord_t    r2 = (dx * dx + dy * dy + dz * dz);

            if(r2 < NBODY_MIN_R)
            {
                r2 = NBODY_MIN_R;
            }

            nbcoord_t    r = sqrt(r2);
            nbcoord_t    coeff = (m2[local_n2]) / (r * r2);

            dx *= coeff;
            dy *= coeff;
            dz *= coeff;

            local_res_x -= dx;
            local_res_y -= dy;
            local_res_z -= dz;
        }

        // Synchronize local work-items computations
        barrier(CLK_LOCAL_MEM_FENCE);

        res_x += local_res_x;
        res_y += local_res_y;
        res_z += local_res_z;
    }

    frx[n1] = vx[n1];
    fry[n1] = vy[n1];
    frz[n1] = vz[n1];
    fvx[n1] = res_x;
    fvy[n1] = res_y;
    fvz[n1] = res_z;
}

CUDA

Реализация для платформы NVidia CUDA немного проще, чем OpenCL, нам не нужно самим создавать контекст устройства и управлять очередью выполнения (по крайней мере, пока мы не захотим сделать multi-GPU реализацию). Как и в случае с OpenCL, нам необходимо выделить память на GPU, скопировать в неё наши данные, и потом можно запускать вычислительное ядро.

Детальнее о работе с CUDA можно прочитать здесь.

Код запуска CUDA ядра

dim3	grid(count / block_size);
dim3	block(block_size);
size_t	shared_size(4 * sizeof(nbcoord_t) * block_size);

kfcompute <<< grid, block, shared_size >>> (...параметры ядра...);

В отличие от OpenCL, в CUDA задаётся не полный диапазон итераций (в OpenCL реализации это global_range), а задаётся размер грида и размеры блока в гриде, соответственно немного меняется вычисление текущего номера тела, в остальном ядро очень похоже на OpenCL, за исключением других имён функций синхронизации и спецификатора для разделяемой памяти. Ещё полезной отличительной особенностью CUDA является то, что мы можем указывать необходимый размер разделяемой памяти при запуске ядра. Как и в OpenCL реализации, в начале каждого блока итераций мы копируем часть данных в разделяемую память и потом работаем с этой памятью из всех нитей блока.

Код CUDA ядра

__global__ void kfcompute(int offset_n2, const nbcoord_t* y, int yoff, nbcoord_t* f, int foff,
                          const nbcoord_t* mass, int points_count, int stride)
{
    int n1 = blockDim.x * blockIdx.x + threadIdx.x;

    const nbcoord_t*    rx = y + yoff;
    const nbcoord_t*    ry = rx + stride;
    const nbcoord_t*    rz = rx + 2 * stride;

    nbcoord_t    x1 = rx[n1];
    nbcoord_t    y1 = ry[n1];
    nbcoord_t    z1 = rz[n1];

    nbcoord_t    res_x = 0.0;
    nbcoord_t    res_y = 0.0;
    nbcoord_t    res_z = 0.0;

    extern __shared__ nbcoord_t shared_xyzm_buf[];

    nbcoord_t*    x2 = shared_xyzm_buf;
    nbcoord_t*    y2 = x2 + blockDim.x;
    nbcoord_t*    z2 = y2 + blockDim.x;
    nbcoord_t*    m2 = z2 + blockDim.x;

    for(int b2 = 0; b2 < points_count; b2 += blockDim.x)
    {
        int            n2 = b2 + offset_n2 + threadIdx.x;

        // Copy data block to local memory
        x2[ threadIdx.x ] = rx[n2];
        y2[ threadIdx.x ] = ry[n2];
        z2[ threadIdx.x ] = rz[n2];
        m2[ threadIdx.x ] = mass[n2];

        // Synchronize local work-items copy operations
        __syncthreads();

        nbcoord_t    local_res_x = 0.0;
        nbcoord_t    local_res_y = 0.0;
        nbcoord_t    local_res_z = 0.0;

        for(int n2 = 0; n2 != blockDim.x; ++n2)
        {
            nbcoord_t    dx = x1 - x2[n2];
            nbcoord_t    dy = y1 - y2[n2];
            nbcoord_t    dz = z1 - z2[n2];
            nbcoord_t    r2 = (dx * dx + dy * dy + dz * dz);

            if(r2 < NBODY_MIN_R)
            {
                r2 = NBODY_MIN_R;
            }

            nbcoord_t    r = sqrt(r2);
            nbcoord_t    coeff = (m2[n2]) / (r * r2);

            dx *= coeff;
            dy *= coeff;
            dz *= coeff;

            local_res_x -= dx;
            local_res_y -= dy;
            local_res_z -= dz;
        }

        // Synchronize local work-items computations
        __syncthreads();

        res_x += local_res_x;
        res_y += local_res_y;
        res_z += local_res_z;
    }

    n1 += foff;
    f[n1 + 3 * stride] = res_x;
    f[n1 + 4 * stride] = res_y;
    f[n1 + 5 * stride] = res_z;
}

Таблица 3. Зависимость времени вычисления (в секундах) функции $inline$ от количества взаимодействующих тел $inline$ для различных GPU реализаций и лучшей CPU реализации

$inline$	4096	8192	16384	32768	65536	131072
openmp+block+optimization	0.0128	0.0495	0.194	0.774	---	---
OpenCL+половинка NVidia K80	0.004	0.008	0.026	0.134	0.322	1.18
CUDA+половинка NVidia K80	0.004	0.008	0.0245	0.115	0.291	1.13

Где взять NVidia K80

OpenCL и CUDA реализации запускались на бесплатном сервисе Colab от Google, который предоставляет доступ к вычислителям NVidia K80. Подробнее о работе с этим сервисом можно прочитать на хабре.

В целом результат неутешительный, всего лишь в 5-6 раз быстрее, чем CPU реализация. Даже если мы будем вести расчёты на всей K80, то получим ускорение до 12 раз, но т.к. сложность задачи квадратична, то мы за разумное время сможем обрабатывать не 32768 взаимодействующих тел, а 131072, что только в 4 раза больше.

Аппроксимация функции $inline$

Если присмотреться к функции, которой задаётся сила притяжения двух тел, то видно, что она квадратично убывает с расстоянием. Поэтому мы можем точно вычислять силу взаимодействия между близкими телами, и приближённо между отдалёнными. Одним из известных подходов
является алгоритм treecode, предложенный Д. Барнсом и П. Хатом. В моделируемом пространстве строится октодерево, содержащее в своих листьях координаты и массы моделируемых тел. В родительских узлах содержится центр масс, общая масса дочерних узлов и радиус сферы, описанной вокруг тел дочерних узлов. Корень дерева содержит центр масс всех тел, их общую массу и радиус сферы, описанной вокруг них. При расчёте силы взаимодействия сначала считается расстояние до корня дерева, если отношение расстояния до узла к его радиусу больше некоторой константы $\lambda_{crit}$ , то корень считается одним телом с координатами, равными координатам центра масс входящих в него тел, и массой, равной сумме масс дочерних узлов, если отношение меньше или равно $\lambda_{crit}$ , то процедура рекурсивно повторяется для каждого дочернего узла. Если достигается лист дерева, то сила взаимодействия считается обычным способом. Таким образом, если одно тело сильно удалено от компактной группы других тел, эта группа представляется для него в виде одного тела, и сила взаимодействия рассчитывается не до каждого тела, а только до одного тела. Благодаря этому сложность алгоритма уменьшается с $inline$ до $O(N \log(N))$ ценой некоторой потери точности.

В своём подходе я решил использовать не октодерево, а kd-дерево т.к. оно проще в использовании и имеет более низкие накладные расходы на хранение по сравнению с октодеревом.

Вернёмся обратно к реализации на CPU. Узел kd-дерева можно представить в виде класса, содержащего указатели на левого и правого потомка и информацию о координатах и массе:

Узел kd-дерева

class node
{
    node*      m_left;  //!< Левый потомок
    node*      m_right; //!< Правый потомок
    nbvertex_t m_mass_center;  //!< Координаты центра масс узла
    nbcoord_t  m_mass; //!< Масса узла
    nbcoord_t  m_radius_sqr; //!< Квадрат радиуса описанной сферы, умноженный на lambda_crit
    nbvertex_t m_bmin; //!< Минимальные координаты описанного бокса
    nbvertex_t m_bmax; //!< Максимальные координаты описанного бокса
    size_t     m_body_n; //!< Номер тела, связанного с узлом
};

При таком способе хранения дерева у нас имеется два возможных варианта обхода дерева: либо использовать явную рекурсию, либо использовать стек самим. Я остановился на втором варианте.

Вычисление силы взаимодействия путем обхода дерева

nbvertex_t force_compute(const nbvertex_t& v1,
                         const nbcoord_t mass1)
{
    nbvertex_t  total_force;
    node*       stack_data[MAX_STACK_SIZE] = {};
    node**      stack = stack_data;
    node**      stack_head = stack;

    *stack++ = m_root;
    while(stack != stack_head)
    {
        node*            curr = *--stack;
        const nbcoord_t  distance_sqr((v1 - curr->m_mass_center).norm());

        if(distance_sqr > curr->m_radius_sqr)
        {//Узел достаточно далеко, вычисляем силу и пропускаем его детей
            total_force += force(v1, curr->m_mass_center, mass1, curr->m_mass);
        }
        else
        {// Узел слишком близко, запоминаем детей для последующей обработки
            if(curr->m_right != NULL)
            {
                *stack++ = curr->m_right;
            }
            if(curr->m_left != NULL)
            {
                *stack++ = curr->m_left;
            }
        }
    }
    return total_force;
}

Как и в cлучае «точной» CPU реализации, функция вычисления силы вызывается для каждого тела. Цикл по всем телам может быть легко распараллелен с помощью директив OpenMP.

Но соседние итерации цикла в этом случае будут обращаться к совершенно разным частям дерева, что не даёт эффективно использовать кэш процессора. Для преодоления этой проблемы обход всех тел нужно производить не по исходному порядку, а по порядку, по которому тела расположены в листьях kd-дерева, тогда соседние итерации будут происходить для тел, находящихся близко в пространстве, и обходить дерево по почти одинаковым путям.

Обход листьев дерева

template<class Visitor>
void traverse(Visitor visit)
{
    node*    stack_data[MAX_STACK_SIZE] = {};
    node**    stack = stack_data;
    node**    stack_head = stack;

    *stack++ = m_root;
    while(stack != stack_head)
    {
        node*                curr = *--stack;
        if(curr->m_radius_sqr > 0)
        {//Это не лист. Откладываем детей на стек.
            if(curr->m_left != NULL)
            {
                *stack++ = curr->m_left;
            }
            if(curr->m_right != NULL)
            {
                *stack++ = curr->m_right;
            }
        }
        else
        {// Это листовой узел. Вычисляем силу.
            visit(curr->m_body_n, curr->m_mass_center, curr->m_mass);
        }
    }
}

Эта реализация имеет другую проблему — нет универсального способа распараллелить такой обход дерева. Но мы можем полностью изменить способ хранения дерева в памяти — мы можем хранить все узлы в одном линейном масиве и полностью отказаться от хранения указателей на потомков, по аналогии с построением двоичной кучи. При начале нумерации узлов с $inline$ , если узел находится в ячейке номером $inline$ , то его левый потомок находится в ячейке $inline$ , правый потомок в ячейке $inline$ , а родитель в ячейке $inline$ . Правый узел, соответствующий левому с номером $inline$ , будет иметь номер $inline$ . Сам массив будет иметь длину $inline$ , а все листовые узлы будут расположены в последних $inline$ ячейках, причём, близкие в пространстве узлы будут расположены в близких ячейках массива. Функция обхода дерева немного изменится, но основа остаётся прежней:

Вычисление силы путём обхода дерева в массиве

nbvertex_t force_compute(const nbvertex_t& v1, const nbcoord_t mass1)
{
    nbvertex_t total_force;

    size_t     stack_data[MAX_STACK_SIZE] = {};
    size_t*    stack = stack_data;
    size_t*    stack_head = stack;

    *stack++ = NBODY_HEAP_ROOT_INDEX;
    while(stack != stack_head)
    {
        size_t                curr = *--stack;
        const nbcoord_t       distance_sqr((v1 - m_mass_center[curr]).norm());

        if(distance_sqr > m_radius_sqr[curr])
        {
            total_force += force(v1, m_mass_center[curr], mass1, m_mass[curr]);
        }
        else
        {
            size_t    left(left_idx(curr));
            size_t    rght(rght_idx(curr));
            if(rght < m_body_n.size())
            {
                *stack++ = rght;
            }
            if(left < m_body_n.size())
            {
                *stack++ = left;
            }
        }
    }
    return total_force;
}

Но и это ещё не все возможности, которые открывает нам хранение узлов в массиве — мы можем отказаться от стека при обходе. Для этого в ветку кода, в которой мы переходим к детям узла, мы добавляем функцию вычисления следующего узла ( $next_{up}$ ), а в ветку, в которой вычисляем силу взаимодействия, мы добавляем вычисление следующего узла с пропуском текущего поддерева ( $skip_{down}$ ).

Для пропуска текущего поддерева нам нужно спускаться к корню (направление $inline$ ), пока мы находимся в правом потомке, как только мы доходим до левого, то переходим в соответствующее ему правое поддерево (направление $inline$ ), если мы попадаем в корень, то обход дерева завершается.

Код функции пропуска поддерева

index_t skip_down(index_t idx)
{
    // While index is 'right' -> go down
    while(is_right(idx))
    {
        index_t parent = parent_idx(idx);
        // We at root again. Stop traverse.
        if(parent == NBODY_HEAP_ROOT_INDEX)
        {
            return NBODY_HEAP_ROOT_INDEX;
        }
        idx = parent;
    }
    return left2right(idx);
}

Рис 8. Пропуск поддерева $skip_{down}$ .

Для перехода к следующему узлу надо, если возможно, переходить к левому потомку (направление $inline$ ), а если потомка нет, то переходить к следующему узлу 'снизу' при помощи функции $skip_{down}$ .

Код функции перехода к следующему узлу

index_t next_up(index_t idx, index_t tree_size)
{
    index_t left = left_idx(idx);
    if(left < tree_size)
    {
        return left;
    }
    return skip_down(idx);
}

Рис 9. Переходы к следующему узлу $next_{up}$ .

Может показаться, что рекурсию мы заменили на цикл $inline$ в функции $skip_{down}$ , и такая замена ничего не даёт, но давайте посмотрим, как определить, является ли узел с номером $inline$ правым потомком. Это можно сделать, просто проверив его номер на нечётность (правый потомок находится в ячейке $inline$ ), для этого достаточно вычислить $i\&1$ . Т.е. мы делим число $inline$ на два если младщий бит выставлен в единицу. Но это можно сделать и без цикла, во многих процессорах есть инструкция find first set, которая возвращает позицию первого установленного бита, воспользовавшись ей мы сворачиваем цикл в четыре инструкции процессора.

Код оптимизированной функции пропуска поддерева

index_t skip_down(index_t idx)
{
    idx = idx >> (__builtin_ffs(~idx) - 1);
    return left2right(idx);
}

После этого мы можем исключить стек из функции обхода дерева и заменить его на пару $skip_{down} + next_{up}$ , после этого функция выглядит даже проще:

Вычисление силы путём обхода дерева в массиве без использования стека

nbvertex_t force_compute(const nbvertex_t& v1,
                         const nbcoord_t mass1) const
{
    nbvertex_t    total_force;
    size_t        curr = NBODY_HEAP_ROOT_INDEX;
    size_t        tree_size = m_mass_center.size();
    do
    {
        const nbcoord_t  distance_sqr((v1 - m_mass_center[curr]).norm());

        if(distance_sqr > m_radius_sqr[curr])
        {
            total_force += force(v1, m_mass_center[curr], mass1, m_mass[curr]);
            curr = skip_down(curr);
        }
        else
        {
            curr = next_up(curr, tree_size);
        }
    }
    while(curr != NBODY_HEAP_ROOT_INDEX);
    return total_force;
}

Всего у нас получилось шесть сочетаний обхода дерева и вычисления силы. Сравним эти подходы по времени вычисления и по качеству. Возъмём как меру качества относительное изменение полной энергии системы после 100 итераций. В качестве модельной системы возьмём две взаимодействующие «галактики», состоящих из $inline$ тел каждая.

Таблица 4. Сочетания способа обхода дерева и вычисления силы

Тип обхода дерева / вычисления силы	Дерево со стеком	'Куча' со стеком	'Куча' без стека
Итерации по номеру тела	cycle+tree	cycle+heap	cycle+heapstackless
Обход листьев	nestedtree+tree	nestedtree+heap	nestedtree+heapstackless


a) Зависимость времени вычисления функции $inline$ от отношения критического расстояния до узла дерева к его радиусу ( $\lambda_{crit}$ ).	b) Зависимость относительного изменения энергии в системе от отношения критического расстояния до узла дерева к его радиусу ( $\lambda_{crit}$ ).
Рис 10. Результаты вычисления функции $inline$ различными способами на CPU (количество тел $inline$ )

Видно, что реализация 'nestedtree+tree' безнадёжно отстала по скорости, т.к. в ней отсутствует параллелизм. Лидируют же реализации с расположением узлов дерева в массиве и индексацией как в двоичной куче. Относительное изменение энергии пренебрежима мала для всех вариантов с $\lambda_{crit} > 1$ . Также на рис. 10a видно, что при ($inline$\lambda_{crit} < 10$inline$) все варианты вычисления функции $inline$ существенно обгоняют по скорости самый оптимизированный вариант точного вычисления ('openmp+block+optimization'), при дальнейшем увеличении $\lambda_{crit}$ реализации с деревом проигрывают точной версии.

Обход дерева на GPU

Обход дерева на GPU я пробовал реализовать как при помощи технологии OpenCL, так и CUDA. Вариант хранения узлов в виде дерева был сразу отброшен, и оставлены были только варианты с хранением дерева в массиве с индексацией как в двоичной куче. В целом, реализации вычислительного ядра не сильно отличаются от CPU версии.

OpenCL ядро для вычисления силы путём обхода дерева (обход по порядку нумерации тел)

__kernel void ComputeTreeBH(int offset_n1, int points_count, int tree_size,
                            __global const nbcoord_t* y,
                            __global nbcoord_t* f,
                            __global const nbcoord_t* tree_cmx,
                            __global const nbcoord_t* tree_cmy,
                            __global const nbcoord_t* tree_cmz,
                            __global const nbcoord_t* tree_mass,
                            __global const nbcoord_t* tree_crit_r2)
{
    int        n1 = get_global_id(0) + offset_n1;
    int        stride = points_count;
    __global const nbcoord_t*    rx = y;
    __global const nbcoord_t*    ry = rx + stride;
    __global const nbcoord_t*    rz = rx + 2 * stride;
    __global const nbcoord_t*    vx = rx + 3 * stride;
    __global const nbcoord_t*    vy = rx + 4 * stride;
    __global const nbcoord_t*    vz = rx + 5 * stride;

    __global nbcoord_t*    frx = f;
    __global nbcoord_t*    fry = frx + stride;
    __global nbcoord_t*    frz = frx + 2 * stride;
    __global nbcoord_t*    fvx = frx + 3 * stride;
    __global nbcoord_t*    fvy = frx + 4 * stride;
    __global nbcoord_t*    fvz = frx + 5 * stride;

    nbcoord_t    x1 = rx[n1];
    nbcoord_t    y1 = ry[n1];
    nbcoord_t    z1 = rz[n1];

    nbcoord_t    res_x = 0.0;
    nbcoord_t    res_y = 0.0;
    nbcoord_t    res_z = 0.0;

    int    stack_data[MAX_STACK_SIZE] = {};
    int    stack = 0;
    int    stack_head = stack;

    stack_data[stack++] = NBODY_HEAP_ROOT_INDEX;
    while(stack != stack_head)
    {
        int          curr = stack_data[--stack];
        nbcoord_t    dx = x1 - tree_cmx[curr];
        nbcoord_t    dy = y1 - tree_cmy[curr];
        nbcoord_t    dz = z1 - tree_cmz[curr];
        nbcoord_t    r2 = (dx * dx + dy * dy + dz * dz);

        if(r2 > tree_crit_r2[curr])
        {
            if(r2 < NBODY_MIN_R)
            {
                r2 = NBODY_MIN_R;
            }

            nbcoord_t    r = sqrt(r2);
            nbcoord_t    coeff = tree_mass[curr] / (r * r2);

            dx *= coeff;
            dy *= coeff;
            dz *= coeff;
            res_x -= dx;
            res_y -= dy;
            res_z -= dz;
        }
        else
        {
            int    left = left_idx(curr);
            int    rght = rght_idx(curr);
            if(left < tree_size)
            {
                stack_data[stack++] = left;
            }
            if(rght < tree_size)
            {
                stack_data[stack++] = rght;
            }
        }
    }

    frx[n1] = vx[n1];
    fry[n1] = vy[n1];
    frz[n1] = vz[n1];
    fvx[n1] = res_x;
    fvy[n1] = res_y;
    fvz[n1] = res_z;
}

В первом варианте обход дерева начинался по порядку нумерации тел в исходном массиве, поэтому соседние нити обходили совершенно разные участки дерева, что отрицательно сказывалось на производительности кэш памяти GPU. Поэтому во втором варианте был применён обход, начинающийся с вершины дерева, в этом случае соседние нити начинают обход дерева по одинаковому пути, т.к. соседние вершины дерева находятся поблизости и в пространстве. Также важно, что мы выбрали нумерацию в массиве узлов дерева не с нуля, а с единицы, в этом случае листья дерева хранятся во второй половине массива, и при количестве тел, равному степени двойки, у нас будет выровненный доступ к памяти по индексу tn1.

OpenCL ядро для вычисления силы путём обхода дерева (обход по порядку нумерации узлов дерева)

__kernel void ComputeHeapBH(int offset_n1, int points_count, int tree_size,
                            __global const nbcoord_t* y,
                            __global nbcoord_t* f,
                            __global const nbcoord_t* tree_cmx,
                            __global const nbcoord_t* tree_cmy,
                            __global const nbcoord_t* tree_cmz,
                            __global const nbcoord_t* tree_mass,
                            __global const nbcoord_t* tree_crit_r2,
                            __global const int* body_n)
{
    int        tree_offset = points_count - 1 + NBODY_HEAP_ROOT_INDEX;
    int        stride = points_count;
    int        tn1 = get_global_id(0) + offset_n1 + tree_offset;

    int          n1 = body_n[tn1];
    nbcoord_t    x1 = tree_cmx[tn1];
    nbcoord_t    y1 = tree_cmy[tn1];
    nbcoord_t    z1 = tree_cmz[tn1];

    nbcoord_t    res_x = 0.0;
    nbcoord_t    res_y = 0.0;
    nbcoord_t    res_z = 0.0;

    int stack_data[MAX_STACK_SIZE] = {};
    int    stack = 0;
    int    stack_head = stack;

    stack_data[stack++] = NBODY_HEAP_ROOT_INDEX;
    while(stack != stack_head)
    {
        int          curr = stack_data[--stack];
        nbcoord_t    dx = x1 - tree_cmx[curr];
        nbcoord_t    dy = y1 - tree_cmy[curr];
        nbcoord_t    dz = z1 - tree_cmz[curr];
        nbcoord_t    r2 = (dx * dx + dy * dy + dz * dz);

        if(r2 > tree_crit_r2[curr])
        {
            if(r2 < NBODY_MIN_R)
            {
                r2 = NBODY_MIN_R;
            }

            nbcoord_t    r = sqrt(r2);
            nbcoord_t    coeff = tree_mass[curr] / (r * r2);

            dx *= coeff;
            dy *= coeff;
            dz *= coeff;
            res_x -= dx;
            res_y -= dy;
            res_z -= dz;
        }
        else
        {
            int    left = left_idx(curr);
            int    rght = rght_idx(curr);
            if(left < tree_size)
            {
                stack_data[stack++] = left;
            }
            if(rght < tree_size)
            {
                stack_data[stack++] = rght;
            }
        }
    }

    __global const nbcoord_t*    vx = y + 3 * stride;
    __global const nbcoord_t*    vy = y + 4 * stride;
    __global const nbcoord_t*    vz = y + 5 * stride;

    __global nbcoord_t*    frx = f;
    __global nbcoord_t*    fry = frx + stride;
    __global nbcoord_t*    frz = frx + 2 * stride;
    __global nbcoord_t*    fvx = frx + 3 * stride;
    __global nbcoord_t*    fvy = frx + 4 * stride;
    __global nbcoord_t*    fvz = frx + 5 * stride;

    frx[n1] = vx[n1];
    fry[n1] = vy[n1];
    frz[n1] = vz[n1];
    fvx[n1] = res_x;
    fvy[n1] = res_y;
    fvz[n1] = res_z;
}

При обходе по порядку нумерации узлов дерева мы получили прирост производительости. Но этот вариант тоже можно улучшить. Глобальная память, в которой сейчас располагаются узлы дерева, оптимизирована для коллективного доступа, т.е. нити одной группы должны читать слова, расположенные в одном блоке памяти. В нашем случае, обход дерева начинается по одинаковым путям, и мы запрашиваем одинаковые данные всеми нитями группы, но чем дальше мы углубляемся в дерево, тем пути соседних нитей всё больше расходятся, и нам приходится запрашивать разные данные, что в несколько раз снижает производительность подсистемы памяти. Но узлы каждого поддерева, принадлежащие одному уровню, располагаются в относительно близких ячейках памяти. Т.е. при обходе оставшейся части дерева соседние нити вычислительного ядра обращаются не к одинаковым узлам дерева, но к близко расположенным в памяти. Для оптимизации такого доступа к памяти можно применить текстурную память. Но есть одна загвоздка. На текущий момент текстуры не поддерживают работу с данными двойной точности (мы же хотим точно вести расчёты). Но в CUDA есть функция __hiloint2double, которая собирает число двойной точности из двух целых чисел.

Код запроса чисел двойной точности из текстуры, хранящей целые числа

template<>
struct nb1Dfetch<double>
{
    typedef double4 vec4;
    static __device__ double fetch(cudaTextureObject_t tex, int i)
    {
        int2 p(tex1Dfetch<int2>(tex, i));
        return __hiloint2double(p.y, p.x);
    }
    static __device__ vec4 fetch4(cudaTextureObject_t tex, int i)
    {
        int        ii(2 * i);
        int4    p1(tex1Dfetch<int4>(tex, ii));
        int4    p2(tex1Dfetch<int4>(tex, ii + 1));
        vec4    d4 = {__hiloint2double(p1.y, p1.x),
                      __hiloint2double(p1.w, p1.z),
                      __hiloint2double(p2.y, p2.x),
                      __hiloint2double(p2.w, p2.z)
                  };
        return d4;
    }
};

При этом было сделано две реализации, в одной каждый элемент дерева (x, y, z, tree_crit_r2) запрашивался независимо, а во второй реализации эти запросы были объединены. Запрос массы узла происходит значительно реже, только при выполнении условия r2 > tree_crit_r2[curr], поэтому не имеет смысла объединять этот запрос с остальными. Ещё одной полезной функцией фреймворка CUDA является возможность регулирования соотношения размеров кэша L1 и размера разделяемой памяти (cudaFuncSetCacheConfig). В случае обхода дерева мы не используем разделяемую память, поэтому мы можем увеличить кэш L1 в ущерб ей.

CUDA ядро для вычисления силы путём обхода дерева (обход по порядку нумерации узлов дерева)

__global__ void kfcompute_heap_bh_tex(int offset_n1, int points_count, int tree_size,
                                      nbcoord_t* f,
                                      cudaTextureObject_t tree_xyzr,
                                      cudaTextureObject_t tree_mass,
                                      const int* body_n)
{
    nb1Dfetch<nbcoord_t>    tex;
    int        tree_offset = points_count - 1 + NBODY_HEAP_ROOT_INDEX;
    int        stride = points_count;
    int        tn1 = blockDim.x * blockIdx.x + threadIdx.x + offset_n1 + tree_offset;

    int          n1 = body_n[tn1];
    nbvec4_t     xyzr = tex.fetch4(tree_xyzr, tn1);
    nbcoord_t    x1 = xyzr.x;
    nbcoord_t    y1 = xyzr.y;
    nbcoord_t    z1 = xyzr.z;

    nbcoord_t    res_x = 0.0;
    nbcoord_t    res_y = 0.0;
    nbcoord_t    res_z = 0.0;

    int stack_data[MAX_STACK_SIZE] = {};
    int stack = 0;
    int stack_head = stack;

    stack_data[stack++] = NBODY_HEAP_ROOT_INDEX;
    while(stack != stack_head)
    {
        int            curr = stack_data[--stack];
        nbvec4_t    xyzr2 = tex.fetch4(tree_xyzr, curr);
        nbcoord_t    dx = x1 - xyzr2.x;
        nbcoord_t    dy = y1 - xyzr2.y;
        nbcoord_t    dz = z1 - xyzr2.z;
        nbcoord_t    r2 = (dx * dx + dy * dy + dz * dz);

        if(r2 > xyzr2.w)
        {
            if(r2 < NBODY_MIN_R)
            {
                r2 = NBODY_MIN_R;
            }

            nbcoord_t    r = sqrt(r2);
            nbcoord_t    coeff = tex.fetch(tree_mass, curr) / (r * r2);

            dx *= coeff;
            dy *= coeff;
            dz *= coeff;
            res_x -= dx;
            res_y -= dy;
            res_z -= dz;
        }
        else
        {
            int    left = nbody_heap_func<int>::left_idx(curr);
            int    rght = nbody_heap_func<int>::rght_idx(curr);
            if(left < tree_size)
            {
                stack_data[stack++] = left;
            }
            if(rght < tree_size)
            {
                stack_data[stack++] = rght;
            }
        }
    }

    f[n1 + 3 * stride] = res_x;
    f[n1 + 4 * stride] = res_y;
    f[n1 + 5 * stride] = res_z;
}

Анализ программы в профилировщике nvprof показал, что даже при использовании текстурной памяти для хранения дерева всё равно очень высокая нагрузка на глобальную память.

Действительно, в CUDA вся память ядра, которая адресуется по 'вычисляемым' адресам, хранится в глобальной памяти, и соответственно стек, который нужен для обхода дерева, расположен в глобальной памяти и 'отъедает' значительную часть пропускной способности чипов памяти, ведь стек есть у каждой выполняемой нити, а нитей очень много.

Но, к счастью, мы уже умеем обходить дерево без использования стека. Дополняя предыдущее вычислительное ядро функциями вычисления следующего узла дерева, получаем новое ядро, причём, более компактное.

CUDA ядро для вычисления силы путём обхода дерева без использования стека

__global__ void kfcompute_heap_bh_stackless(int offset_n1, int points_count, int tree_size,
                                            nbcoord_t* f,
                                            cudaTextureObject_t tree_xyzr,
                                            cudaTextureObject_t tree_mass,
                                            const int* body_n)
{
    nb1Dfetch<nbcoord_t>    tex;
    int        tree_offset = points_count - 1 + NBODY_HEAP_ROOT_INDEX;
    int        stride = points_count;
    int        tn1 = blockDim.x * blockIdx.x + threadIdx.x + offset_n1 + tree_offset;

    int          n1 = body_n[tn1];
    nbvec4_t     xyzr = tex.fetch4(tree_xyzr, tn1);
    nbcoord_t    x1 = xyzr.x;
    nbcoord_t    y1 = xyzr.y;
    nbcoord_t    z1 = xyzr.z;

    nbcoord_t    res_x = 0.0;
    nbcoord_t    res_y = 0.0;
    nbcoord_t    res_z = 0.0;

    int    curr = NBODY_HEAP_ROOT_INDEX;
    do
    {
        nbvec4_t     xyzr2 = tex.fetch4(tree_xyzr, curr);
        nbcoord_t    dx = x1 - xyzr2.x;
        nbcoord_t    dy = y1 - xyzr2.y;
        nbcoord_t    dz = z1 - xyzr2.z;
        nbcoord_t    r2 = (dx * dx + dy * dy + dz * dz);

        if(r2 > xyzr2.w)
        {
            if(r2 < NBODY_MIN_R)
            {
                r2 = NBODY_MIN_R;
            }

            nbcoord_t    r = sqrt(r2);
            nbcoord_t    coeff = tex.fetch(tree_mass, curr) / (r * r2);

            dx *= coeff;
            dy *= coeff;
            dz *= coeff;
            res_x -= dx;
            res_y -= dy;
            res_z -= dz;
            curr = nbody_heap_func<int>::skip_idx(curr);
        }
        else
        {
            curr = nbody_heap_func<int>::next_up(curr, tree_size);
        }
    }
    while(curr != NBODY_HEAP_ROOT_INDEX);

    f[n1 + 3 * stride] = res_x;
    f[n1 + 4 * stride] = res_y;
    f[n1 + 5 * stride] = res_z;
}

Производительность ядер, выполняемых на GPU, сильно зависит от размера блоков, на которые мы делим задачу. От этого размера зависит, сколько регистров, локальной памяти и прочих ресурсов будет доступно каждой вычислительной нити. Также нужно иметь в виду, что во время ожидания доступа к памяти в одной нити, другая нить может производить вычисления на шейдерном процессоре, таким образом, при достаточном количестве одновременно выполняемых нитей на одном процессоре время доступа к памяти будет скрыто за вычисленими. Поэтому перед сравнением производительности наших ядер нам надо для каждого из них вычислить оптимальный размер блока. Произведём сравнение на доступной нам половинке от NVidia K80.

Таблица 5. Зависимость времени вычисления (в секундах) функции $inline$ от размера блока для различных GPU реализаций при количестве тел $inline$ и $\lambda_{crit}=10$

Размер блока/ядро	8	16	32	64	128	256	512	1024
opencl+dense	5.77	2.84	1.46	1.13	1.15	1.14	1.14	1.13
cuda+dense	5.44	2.55	1.27	0.96	0.97	0.99	0.99	-
opencl+heap+cycle	5.88	5.65	5.74	5.96	5.37	5.38	5.35	5.38
opencl+heap+nested	4.54	3.68	3.98	5.25	5.46	5.41	5.48	5.31
cuda+heap+nested	3.62	2.81	2.68	4.26	4.84	4.75	4.8	4.67
cuda+heap+nested+tex	2.6	1.51	0.912	0.7	1.85	1.75	1.69	1.61
cuda+heap+nested+tex+stackless	2.3	1.29	0.773	0.5	0.51	0.52	0.52	0.52

Таблица 6. Зависимость времени вычисления (в секундах) функции $inline$ от размера блока для различных GPU реализаций при количестве тел $inline$ и $\lambda_{crit}=4$

Размер блока/ядро	8	16	32	64	128	256	512	1024
opencl+dense	366	179	89.9	69.3	70.3	69.1	68.9	68.0
cuda+dense	346	162	79.6	60.8	60.8	60.7	59.6	-
opencl+heap+cycle	16.2	18.2	20.1	21.2	21.2	21.3	21.2	21.1
opencl+heap+nested	10.5	7.63	6.38	8.23	9.95	9.89	9.65	9.66
cuda+heap+nested	8.67	6.44	5.39	5.93	8.65	8.61	8.41	8.27
cuda+heap+nested+tex	6.38	3.57	2.13	1.44	3.56	3.46	3.30	3.29
cuda+heap+nested+tex+stackless	5.78	3.19	1.83	1.21	1.11	1.10	1.11	1.13

Сложная ситуация, но, в отличие, от CPU версии обхода дерева, видно, что каждый шаг оптимизации приносит ощутимые плоды. Реализация 'opencl+heap+cycle' почти в 6 раз медленнее точного решения с полным вычислением функции $inline$ . Реализация 'opencl+heap+nested', в которой обход дерева начинается с соседних узлов, быстрее предыдушей в 1.4 раза, т.к. лучше задействуется кэш память. В реализации 'cuda+heap+nested' увеличен кэш L1 в ущерб разделяемой памяти, что дало прирост скорости ещё в 1.4 раза, хотя не исключено, что в cuda реализации более оптимально скомпилированно вычислительное ядро (в версиях 'opencl+dense' и 'cuda+dense' ядра идентичные, а быстродействие у cuda версии выше в ~1.2 раза). Самый существенный прирост скорости вычислений (в 3.8 раза) достигается при расположении дерева в текстурной памяти и объединении запросов к элементам узла дерева. Реализация с обходом дерева без использования стека 'cuda+heap+nested+tex+stackless' быстрее ещё в 1.4 раза, т.к. в ней вся пропускная способность шины памяти используется только для доступа к данным об узлах дерева и не расходуется на стек. Таким образом, при $\lambda_{crit}=10$ удалось достичь ускорения в два раза по сравнению с полным вычислением функции $inline$ . Но $\lambda_{crit}=10$ избыточно большое значение параметра, на графике зависимости относительного изменения энергии в системе от отношения критического расстояния до узла дерева к его радиусу для CPU реализации видно, что можно использовать более низкие значения $\lambda_{crit}$ без видимой потери точности решения. Попробуем поварьировать $\lambda_{crit}$ при оптимальных размерах блока, которые мы определили на предыдущем шаге.


a) $inline$	b) $inline$
Рис 11. Зависимость времени вычисления функции $inline$ от отношения критического расстояния до узла дерева к его радиусу ( $\lambda_{crit}$ ) для различных GPU реализаций обхода дерева

Видно, что при малых $\lambda_{crit}$ все способы вычисления функции $inline$ выходят на близкие значения, определяемые временем построения kd-дерева и подготовкой данных для GPU. Причём, время построения дерева вносит весомый вклад в общее время до $\lambda_{crit}\leq 4$ , далее этим временем можно пренебречь. Интересно заметить, что при $inline$ производительность опять улучшается при достижении $\lambda_{crit}=1024$ , скорее всего это обусловлено тем, что все нити GPU обходят одни и те же вершины дерева одновременно, что улучшает использование кэша L1 и полностью исключает 'branch divergence'. Также видно, что наилучшее быстродействие у реализации без использования стека (cuda+heap+nested+tex+stackless), она обгоняет по скорости вариант со стеком примерно в $inline$ раза. Прочие реализации ещё в несколько раз медленнее. Для закрепления результата проведём расчет времени на GPU с более новой архитектурой.

Результаты запуска на GeForce GTX 1080 Ti (одинарная точность)

Таблица 7. Зависимость времени вычисления (в секундах) функции $inline$ от размера блока для различных GPU реализаций при количестве тел $inline$ и $\lambda_{crit}=4$

Размер блока/ядро	8	16	32	64	128	256	512	1024
opencl+dense	47.8	23.4	11.6	11.59	12.8	12.8	12.8	12.8
cuda+dense	49.0	23.8	11.9	11.8	11.7	11.7	11.7	11.7
opencl+heap+cycle	7.48	8.26	7.73	7.36	7.33	7.27	7.25	7.26
opencl+heap+nested	1.33	1.20	1.41	2.46	2.53	2.49	2.44	2.47
cuda+heap+nested	1.23	1.10	1.31	2.28	2.29	2.28	2.23	2.25
cuda+heap+nested+tex	0.88	0.68	0.654	1.6	1.6	1.6	1.6	1.6
cuda+heap+nested+tex+stackless	0.71	0.47	0.45	0.43	0.43	0.42	0.41	0.395

Рис 12. Зависимость времени вычисления функции $inline$ от отношения критического расстояния до узла дерева к его радиусу ( $\lambda_{crit}$ ) для различных GPU реализаций обхода дерева

При использовании GeForce GTX 1080 Ti для вычисления, разница между реализациями обхода дерева со стеком и без стека достигает двух раз, при условии, что мы пренебрегаем временем построения дерева. Этот факт подталкивает нас к тому, чтобы в будующем перенестии на GPU и построение дерева. Из сравнения таблиц 5-7 видно, что нет единого оптимального размера блока для разного количества тел и тем более для разных архитектур GPU, причём, разница времени вычисления может достигать нескольких раз, даже если не брать в расчёт граничные значения. Таким образом, перед длительными расчетами имеет смысл определять оптимальный размер блока для каждой конфигурации.

Главное, чего мы достигли — это возможность моделировать попарное взаимодействие немногим более миллиона тел ( $2^{20}$ ) за разумное время на одном, не самом новом GPU. На более новых GPU (Tesla V100), видимо, можно будет обрабатывать уже около двух миллионов взаимодействующих тел за разумное время, т.к. их производительность примерно в четыре раза выше, чем у половинки Tesla K80. Хотя, это число ещё и несравнимо с количеством звёзд даже в карликовых галактиках, таких как Малое Магелланово Облако, но, на мой взгляд, является внушительным.

Заключение

Применение вложенных методов решения дифференциальных уравнений позволяет решать подобные задачи с высоким уровнем точности при сравнительно небольших временных затратах, а применение алгоритмов аппроксимации функции вычисления силы попарного притяжения позволяют обрабатывать колоссальные объёмы взаимодействующих тел. Таким образом, в отличие от инопланетян из «Задачи трёх тел», мы в состоянии решить задачу $inline$ тел, и для небольшого числа тел и для целых звёздных скоплений, хотя и ценой некоторой потери точности.

Визуализация

Для тех, кто дочитал до конца приведу ещё несколько видеороликов с визуализацией процесса эволюции систем тел.

Моделирование столкновения двух галактик. Общее количество тел 60 тысяч.

Моделирование эволюции галактики, состоящей из миллиона звёзд. В центре тело с массой 99% от общей. Одиночные частицы практически неразличимы. Уже больше напоминает волны в капле жидкости. Раскрашено в соответствии с модулем скорости. Низкая скорость — синий цвет, средняя — зелёный, высокая — красный. Видно, что в центре скорость выше, и плавно убывает к краям, а самая низкая в экваториальной плоскости.

Более 'динамичное' моделирование эволюции галактики, состоящей из миллиона звёзд. В центре тело с массой 10% от общей. Центральное тело влияет на остальные существенно меньше. Сначала 'звёзды' разлетаются, потом собираются обратно в несколько скоплений, и в конце опять образуют одно большое скопление.

В процессе моделирования порядка 5% 'звёзд' покинуло начальную область безвозвратно.

На 10-й секунде очень напоминает существующую галактику Колесо телеги.

Код проекта можно найти на гитхабе.

Теги:

Хабы: