Магниты были знакомы людям с древнейших времён, но физика ферромагнетизма остаётся загадкой. Теперь знакомая всем головоломка приближает физиков к ответам на вопросы
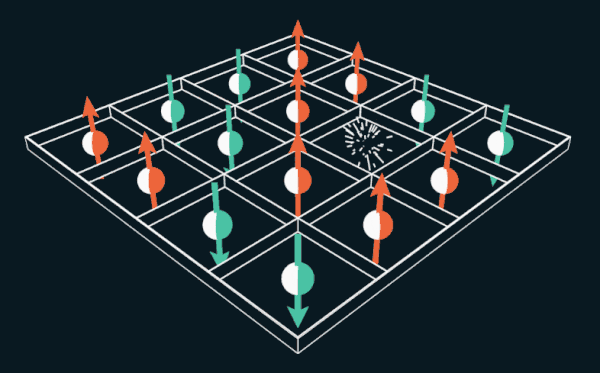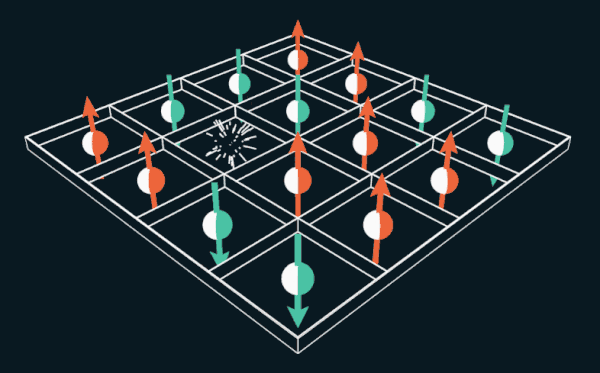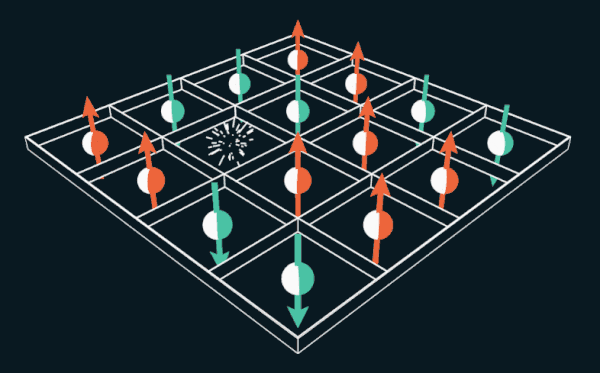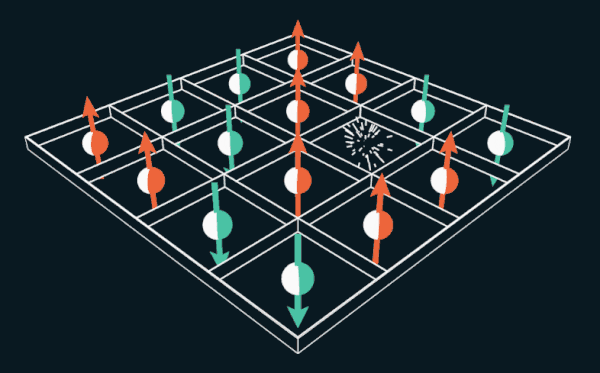
Игра в 15 предлагает игроку сдвигать пронумерованные плитки в рамках решётки. Если заменить номера спинами электронов, головоломку можно будет использовать для объяснения того, как работают постоянные магниты.
На несколько месяцев в 1880-м году целые регионы США поддались пристрастию, аналогов которого ранее никто не видел. «По всей стране буквально разразилась эпидемия», — писал журнал The Weekly News-Democrat города Импория, штата Канзас, 12 марта 1880. «Целые города завлечены, люди теряют сон и сходят с ума». Эпидемия распространилась на Европу, и дошла даже до Австралии с Новой Зеландией.
Заболеванием стала новая страсть: обескураживающее простая механическая игрушка-головоломка «15». Она известна до сих пор, и состоит из поля 4х4 квадрата, в котором можно передвигать 15 пронумерованных плиток с целью расставить их по порядку.
По сегодняшним стандартам игра кажется старомодной, но в 1880-м она была на пике популярности. «Ни один ребёнок не сможет устоять перед таким развлечением, ни один взрослый не окажется настолько сильным или высокомерным, чтобы избежать её очарования», — писала газета. А разочарование, возможно, проистекало из математически доказанного факта, что лишь половина конфигураций этой головоломки можно успешно решить (что, вероятно, было неизвестно попавшим под её влияние).
Сегодня, почти 140 лет спустя, к игре «15» снова возродился интерес, но на этот раз она выступает не в качестве отвлечения, а как способ понять вроде бы не связанную с ней и куда как более сложную головоломку: как работают магниты.
Постоянные магниты, как те, что висят на дверце вашего холодильника, притягиваются благодаря такому явлению, как ферромагнетизм. В ферромагнетике выравниваются спины электронов, и все вместе генерируют магнитное поле. Точнее, такие металлы, как железо, кобальт и никель демонстрируют зонный магнетизм, поскольку их электроны способны свободно двигаться в рамках материала. У каждого электрона есть свой собственный магнитный момент, но чтобы понять, как и почему все эти моменты выстраиваются в магните, требуется вычислить квантовые взаимодействия между всеми электронами, что чрезмерно сложно сделать.
«Зонный магнетизм, на самом деле – одна из сложнейших задач теоретической физики конденсированного состояния», — сказала Вай Ли, физик из Университета Джонса Хопкинса.
Однако Ли и двое аспирантов, Эрик Бобров и Китон Стьюбис, возможно, подошли немножечко ближе к решению этой задачи. Используя математику головоломки «15», они расширили известную теорему, описывающую идеализированное состояние зонного магнетизма. В их новом анализе, опубликованном в журнале Physical Review B, они расширяют теорему, чтобы объяснить более широкую и реалистичную систему, что потенциально может привести к созданию более точной модели работы магнитов.
«Это прекрасная работа», — сказал Дэниел Аровас, физик из Калифорнийского университета в Сан-Диего. «Особенно эта работа нравится мне в связи с тем, что подробных результатов, касающихся зонного магнетизма, слишком мало и они слишком разрознены».
Прыжки по дыркам
На самом базовом уровне электроны в металле должны подчиняться двум крупным ограничениям. Во-первых, все они заряжены отрицательно, поэтому отталкиваются друг от друга. Во-вторых, электроны обязаны подчиняться т.н. принципу Паули, постулирующему, что две частицы [с полуцелым спином / прим. перев.] не могут находиться в одинаковом квантовом состоянии. Это означает, что электроны с одинаковым спином – пропорциональным магнитному моменту электрона — не могут занимать одно и то же состояние в атоме металла. А два электрона с противоположными спинами могут.
Оказывается, что простейшим способом удовлетворить одновременно взаимное отталкивание и ограничения принципа Паули для группы электронов будет находиться по отдельности и выравнивать спины – в результате чего материал становится ферромагнитным.
Однако это лишь упрощённая картина. Физики никак не могли построить подробную модель появления такого организованного рисунка выровненных спинов из бесчисленных квантовых взаимодействий между отдельными электронами. К примеру, как пояснил Ли, волновая функция электрона – сложное математическое описание его квантовых свойств — может быть запутанной с волновой функцией другого электрона. Чтобы досконально разобраться в том, как поведение отдельных частиц приводит к появлению такого коллективного явления, как ферромагнетизм, придётся отслеживать волновую функцию каждого электрона в системе, в то время как она непрерывно меняет волновую функцию каждого из оставшихся электронов в процессе их взаимодействия. На практике такая повсеместная запутанность делает невозможным записать полные и всеобъемлющие уравнения, необходимые для описания ферромагнетизма.
Вместо этого физики, в том числе и Ли, пытаются собрать информацию, изучая упрощённые, идеализированные модели, описывающие физику, лежащую в основе ферромагнетизма. В частности, её последняя работа расширяет важное открытие, сделанное более 50 лет назад.
В середине 1960-х два физика с противоположных сторон земного шара независимо вывели доказательство, объяснявшее, почему электроны должны выравниваться и создавать ферромагнитное состояние. Дэвид Тулес, физик, работавший тогда в Кембриджском университете, который в итоге удостоится нобелевской премии 2016 года, и Йосуке Нагаока, физик из Университета Нагои, гостивший в то время в Калифорнийском университете в Сан-Диего, опубликовали свои доказательства в 1965 и 1966 годах соответственно. Их результат, получивший название теорема Нагаоки-Тулеса (или просто теорема Нагаоки), основывается на идеализированной системе электронов, расположенных на атомной решётке. Так что, хотя она и не объясняет поведение реальных магнитов, она всё равно была важной, впервые в принципе показав, почему спины электронов должны выравниваться. А поскольку их анализ представлял собой математические доказательства, они были точными, не обременёнными типичными для физики приближениями.
Чтобы понять теорему, представьте двумерную квадратную решётку. Каждый узел может разместить два электрона с противоположными спинами, но теорема предполагает, что для размещения двух электронов в одном месте потребуется бесконечное количество энергии. Это гарантирует, что на каждом месте будет находиться только один электрон. В такой конфигурации каждый электрон может направить свой спин либо вверх, либо вниз. Им не обязательно выравниваться, поэтому такая система не должна быть ферромагнетиком.

Вай Ли, физик из Университета Джонса Хопкинса
Теперь уберём один электрон. В результате останется вакантное место, именуемое дыркой. Соседний электрон может соскользнуть в дырку, оставив позади новое пустое место. Другой электрон может переехать в новое пустое место, оставив позади очередную дырку. В таком примере дырка, по сути, прыгает с одного места на другое, перемещаясь по сетке. Тулес и Нагаока обнаружили, что в таком случае при добавлении единственной дырки электроны выровняются спонтанно. Они доказали, что это будет состояние с наименьшей энергией, состояние ферромагнетика.
Аровас объясняет, что для того, чтобы система пришла в состояние с наименьшей энергией, дырка должна иметь возможность свободно перемещаться, не нарушая конфигурацию спинов электронов – такой процесс потребует дополнительной энергии. Но когда двигается дырка, должны двигаться и электроны. Чтобы электроны двигались, не нарушая конфигурации спинов, они должны быть выровнены.
«Теорема Нагаоки – один из немногих примеров, при помощи которых можно математически доказать отдельные случаи ферромагнетизма, — сказал Масаки Ошикава, физик из Токийского университета. – Но с точки зрения физики всё это весьма искусственно».
К примеру, электронам требуется очень много энергии, чтобы преодолеть их взаимное отталкивание и устроиться в одном месте – но не бесконечное, как требует теорема. Кроме того, картина, нарисованная Нагаокой и Тулесом, применима только к простым решёткам: двумерным решёткам, состоящим из квадратов или треугольников, или к трёхмерным кубическим решёткам. В природе же ферромагнетизм возникает во многих металлах со структурами всякого рода.
Если теорема Нагаоки-Тулеса на самом деле объясняет ферромагнетизм, тогда она должна быть применимой ко всем решёткам. Люди предполагали, что так и есть, сказала Ли. «Но никто не дал реального, чёткого доказательства». Ну то есть, до сих пор.
Плитки со спинами
В 1989 Хал Тасаки, физик из японского университета Гакусюин, расширил эту теорему, обнаружив, что она будет применимой, пока у решётки будет такое математическое свойство, как связность. Возьмём простой случай квадратной решётки с одной движущейся дыркой. Если, подвигав дырку, вы можете воспроизвести любую конфигурацию спинов, сохраняя количество электронов, со спинами, направленными как вверх, так и вниз, то условие связности выполняется.
Но кроме квадратных и треугольных решёток, и трёхмерных кубов, было непонятно, будет ли выполняться условие связности в других случаях – и, значит, как широко можно применять эту теорему.
Чтобы разобраться с этим вопросом, Ли начала с шестиугольной решётке из сот. Её студенты, Бобров и Стьюбис, работая над этой задачей, поняли, что она напоминает манию XIX века: головоломку «15». Поменяйте метки плиток с чисел на спины, направленные вверх и вниз, и головоломка становится эквивалентной ферромагнетику Нагаоки, с дыркой, двигающейся по решётке электронов.
Головоломка разрешается, когда у вас есть возможность перераспределить плитки в любой последовательности, что полностью совпадает с условием связности. Так что вопрос о том, удовлетворяется ли для данной решётки условие связности, становится вопросом о том, можно ли решить эквивалентную головоломку на решётке такой структуры.
Оказывается, что в 1974 году математик Ричард Уилсон, работающий ныне в Калифорнийском технологическом институте, решил эту задачу, обобщив и решив головоломку «15» для всех решёток. В рамках доказательства он показал, что почти на всех неразделимых решётках (у которых все узлы остаются связанными даже после удаления одного из них), можно двигать плитки и получить любую конфигурацию, пока количество движений остаётся чётным. Единственное исключение – одиночные многоугольники больше треугольника, и нечто под названием «граф θноль», в котором вершина в центре шестиугольника соединена с двумя противоположными вершинами.
Исследователи смогли напрямую применить доказательство Уилсона к теореме Нагаоки-Тулеса. Они доказали, что условие связности выполняется для системы электронов и единственной дырки почти на всех решётках, включая такие распространённые структуры, как двумерные соты и трёхмерные ромбовидные решётки. Два исключения – многоугольники больше треугольника, и граф θноль – в любом случае не встречаются в реальных ферромагнетиках.
Взрыв дырок
Использование головоломки «15» – это свежий и потенциально плодотворный подход, сказал Срирам Шастри, физик из Калифорнийского университета в Санта-Круз. «Мне нравится то, что он привлекли к работе новый язык, новый набор связей с теорией графов, — сказал он. – Я думаю, что это богатая связь – в будущем она может стать богатым источником идей». Но, хотя исследование делает значительный шаг вперёд, проблемы пока остаются.
Одно из осложнений связано с тем, что теорема Нагаоки-Тулеса не всегда работает, когда движущейся дырке нужно сделать нечётное количество шагов в процессе движения по решётке, сказал Шастри. Возможно, наиболее бросающейся в глаза проблемой будет то, что теореме требуется наличие ровно одной дырки – не больше, не меньше. Однако в металлах полно дырок, они часто занимают до половины решётки.
Но физики пытались обобщить теорему для систем со множеством дырок. Используя численные методы, физики, показали, что ферромагнетизм Нагаоки, судя по всему, работает для квадратной решётки конечного размера, до 30% которой составляют дырки. В текущей работы исследователи применили точные аналитические техники к двумерным сотам и к трёхмерным ромбовидным решёткам. Ферромагнетизм Нагаоки, судя по всему, существует, пока количество дырок не превышает количество узлов решётки в степени 1/2 для сот, и в степени 2/5 для ромбовидной решётки.
Эти точные решения могут привести к созданию более полной модели зонного магнетизма. «Это всего лишь один небольшой шаг к установке строгой математической отправной точки для будущих исследований», — сказала Ли.