Jupyter уже давно зарекомендовал себя как удобную платформу для работы в различных областях на стыке программирования, анализа данных, машинного обучения, математики и других. Вот например очень известная книга по анализу данных, состоящая из Jupyter блокнотов. Поддержка  , markdown, html дает возможность использовать использовать Jupyter в качестве платформы для удобного оформления научного-технического материала. Преимущество таких блокнотов заключается в интерактивности, возможности сопровождать сухой материал примерами программ, при этом эта интерактивность очень естественна и проста в использовании. В этой статье хотелось бы рассказать про возможность создания в Jupyter анимированных примеров работы различных алгоритмов и привести несколько из них с исходным кодом. В качестве кликбейта алгоритм Дейкстры.
, markdown, html дает возможность использовать использовать Jupyter в качестве платформы для удобного оформления научного-технического материала. Преимущество таких блокнотов заключается в интерактивности, возможности сопровождать сухой материал примерами программ, при этом эта интерактивность очень естественна и проста в использовании. В этой статье хотелось бы рассказать про возможность создания в Jupyter анимированных примеров работы различных алгоритмов и привести несколько из них с исходным кодом. В качестве кликбейта алгоритм Дейкстры.
Все примеры, которые будут представлены в статье, можно найти вот в этом ноутбуке, основной материал будет спрятан под спойлерами из-за того, что кода и gif довольно много. Чтобы воспроизвести часть примеров, которые будут представлены в любом случае понадобится этот репозиторий из-за того, что он содержит некоторые промежуточные утилиты.
Под Jupyter есть набор виджетов (ipywidgets), которые представляю собой различного рода инструменты управления, взаимодействуя с модулем IPython.display предоставляют интерактивную визуализацию. Следующий код представляет все ключевое взаимодействие с виджетами, с помощью которого можно сделать интерактивную анимацию на содержимом списка:
Вот что получится, если подать функции animate_list список из целых чисел:

Чтобы продемонстрировать работу какого-либо алгоритма с помощью animate_list нужно сгенерировать промежуточные состояния алгоритма и сохранить их визуальное представление в нужном формате.
Базовые алгоритмы для работы с последовательностями/массивами достаточно текстового представления. У меня к сожалению были проблемы с базовыми строками, которые отказывались обрабатывать перевод строки, в результате я использовал IPython.display.Code. Начнем с классической быстрой сортировки.
Похожим образом можно визуализировать и бинарный поиск
А вот пример для строк: процесс построения префикс-функции:
Matplotlib — библиотека Python для отрисовки различных графиков. Вот несколько примеров как можно её использовать для визуализации алгоритмов. Начнем с примера итеративных алгоритмов поиска минимума функции, наиболее простым из которых является метод случайного локального поиска, которые делает локальное изменение тек��щего приближения и переходит в него если значение значение функции в новой точки оказалось лучше:
А вот пример ЕМ алгоритма для данных извержений Old Faithful гейзера, такой же пример приведен на википедии:
Следующий пример скорее игрушечный, но тоже показывает, что можно сделать в matplotlib: визуализация замощения клетчатой фигуры на плоскости максимальным числом доминошек с помощью нахождения максимального паросочетания:
Ну и попутно демонстрация алгоритма раскраски планарного графа в 5 цветов, чтобы визуально разбиение смотрелось лучше:
Последний пример с matplotlib из вычислительной геометрии — алгоритм Грэхэма-Эндрю для построения выпуклой оболочки на плоскости:
Последнее, что хотелось бы отметить в контексте matplotlib — это альтернативный способ создания анимаций через matplotlib.animation.FuncAnimation. У этого способа есть свои плюсы: его можно конвертировать в html с помощью IPython.display.HTML, результат будет более надежным, чем на виджетах (у меня виджеты периодически торомозят), не будет требовать рабочего ядра Jupyter, но в этом случае анимация стоновится обычным видео и средства управления ограничены проигрывателем.
С помощью graphviz можно отрисовывать графы. Обратите внимание, что для воспроизведения примеров с его помощью необходимо будет установить graphviz не только в python, но и в систему. Начнем с обхода в глубину:
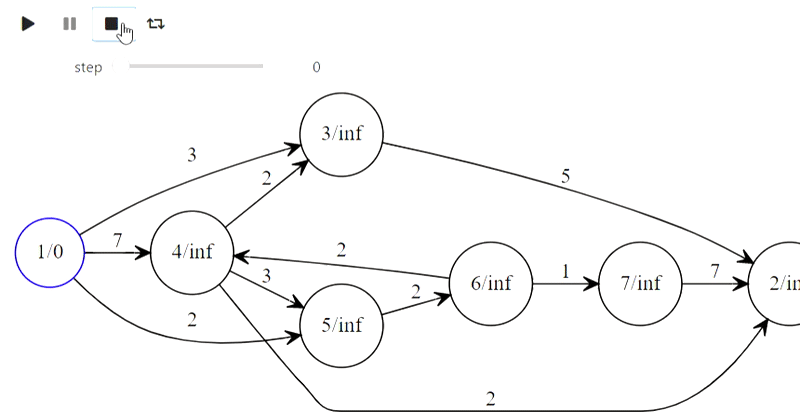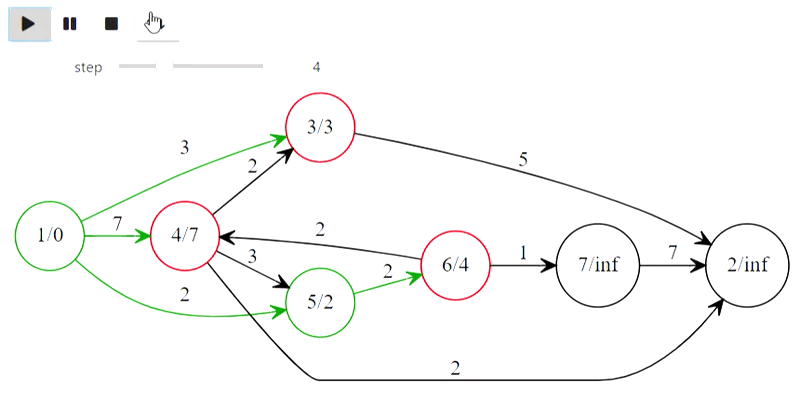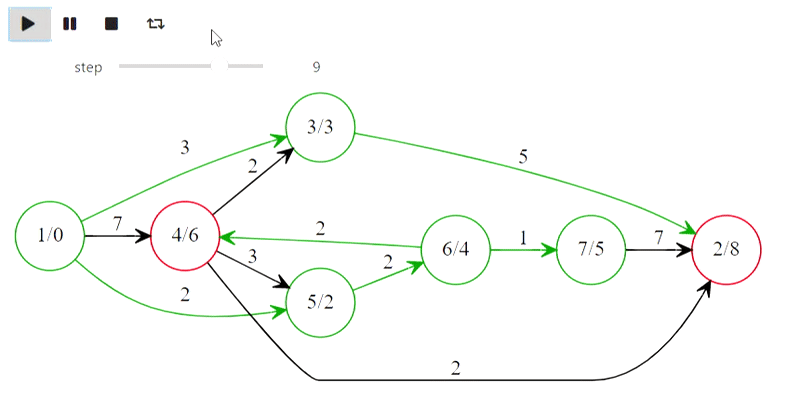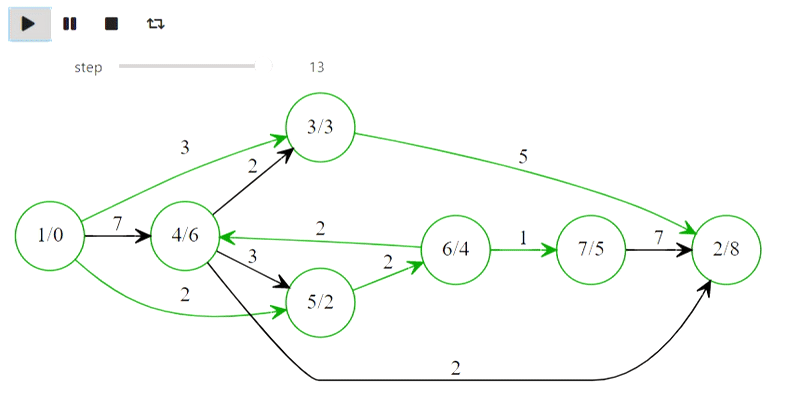
Ну а вот и алгоритм Дейкстры из заголовка
А вот таким образом происходит построение префиксного дерева для слов 'мама', 'мать', 'мартышка', 'мыла', 'молоко':
Ну и напоследок алгоритм Куна для нахождения максимального паросочетания:
А вот эта часть относится к неудавшейся попытке. IPython.display умеет парсить latex, однако при попытки его использовать вот что у меня получилось (должен был быть метод Гаусса):
Пока я не знаю, что с этим делать, но возможно знающие люди подскажут.

Предисловие
Все примеры, которые будут представлены в статье, можно найти вот в этом ноутбуке, основной материал будет спрятан под спойлерами из-за того, что кода и gif довольно много. Чтобы воспроизвести часть примеров, которые будут представлены в любом случае понадобится этот репозиторий из-за того, что он содержит некоторые промежуточные утилиты.
Чем анимируем
Под Jupyter есть набор виджетов (ipywidgets), которые представляю собой различного рода инструменты управления, взаимодействуя с модулем IPython.display предоставляют интерактивную визуализацию. Следующий код представляет все ключевое взаимодействие с виджетами, с помощью которого можно сделать интерактивную анимацию на содержимом списка:
from ipywidgets import interact, interactive, fixed, interact_manual
import ipywidgets as widgets
from IPython.display import display
def step_slice(lst, step):
return lst[step]
def animate_list(lst, play=False, interval=200):
slider = widgets.IntSlider(min=0, max=len(lst) - 1, step=1, value=0)
if play:
play_widjet = widgets.Play(interval=interval)
widgets.jslink((play_widjet, 'value'), (slider, 'value'))
display(play_widjet)
# slider = widgets.Box([play_widject, slider])
return interact(step_slice,
lst=fixed(lst),
step=slider)
Вот что получится, если подать функции animate_list список из целых чисел:
a = [10, 9, 8, 7, 6, 5, 4, 3, 2, 1]
animate_list(a, play=True, interval=200);

Чтобы продемонстрировать работу какого-либо алгоритма с помощью animate_list нужно сгенерировать промежуточные состояния алгоритма и сохранить их визуальное представление в нужном формате.
Тектовые анимации
Базовые алгоритмы для работы с последовательностями/массивами достаточно текстового представления. У меня к сожалению были проблемы с базовыми строками, которые отказывались обрабатывать перевод строки, в результате я использовал IPython.display.Code. Начнем с классической быстрой сортировки.
Код
from IPython.display import Code
import random
def qsort_state(array, left, right, x, p, q):
extended_array = list(map(str, array[:left])) + ['['] + list(map(str, array[left: right])) + [']'] + list(map(str, array[right:]))
offset_x = sum(list(map(len, extended_array[:left]))) + left + 2
zero_line = ''.join([' ' for i in range(offset_x)]) + f'x = {x}'
first_line = ' '.join(extended_array)
offset_p = sum(list(map(len, extended_array[:p + 1]))) + p + 1 + len(extended_array[p + 1]) // 2
offset_q = sum(list(map(len, extended_array[:q + 1]))) + q + 1 + len(extended_array[q + 1]) // 2
second_line = ''.join([' ' if i != offset_p and i != offset_q else '↑' for i in range(len(first_line))])
return Code(zero_line + '\n' + first_line + '\n' + second_line)
def qsort(array, left, right, states):
if right - left <= 1:
return
x = array[random.randint(left, right - 1)]
p = left
q = right - 1
states.append(qsort_state(array, left, right, x, p, q))
while p <= q:
while array[p] < x:
p += 1
states.append(qsort_state(array, left, right, x, p, q))
while array[q] > x:
q -= 1
states.append(qsort_state(array, left, right, x, p, q))
if p <= q:
array[p], array[q] = (array[q], array[p])
states.append(qsort_state(array, left, right, x, p, q))
p += 1
q -= 1
if p <= q:
states.append(qsort_state(array, left, right, x, p, q))
qsort(array, left, q + 1, states)
qsort(array, p, right, states)
a = [234, 1, 42, 3, 15, 3, 10, 9, 2]
states = []
qsort(a, 0, len(a), states)
animate_list(states, play=True);
Результат
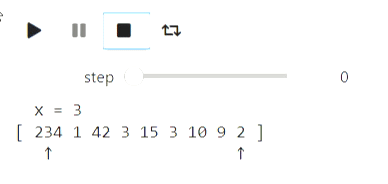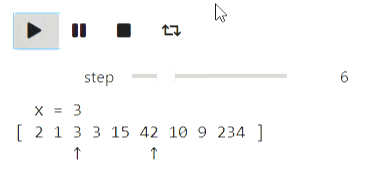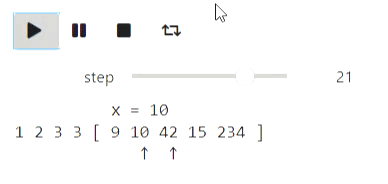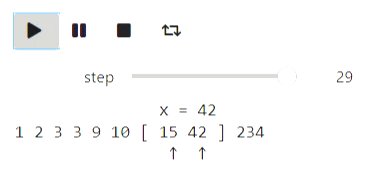

Похожим образом можно визуализировать и бинарный поиск
Код
def bs_state(array, left, right, x):
extended_array = list(map(str, array[:left])) + ['['] + list(map(str, array[left: right])) + [']'] + list(map(str, array[right:]))
mid = (left + right) // 2
offset_x = sum(list(map(len, extended_array[:mid + 1]))) + mid + 1
return Code(' '.join(extended_array) + '\n' + ''.join([' ' for i in range(offset_x)]) + str(x))
# Эта версия бинарного поиска находит последний элемент, который
# меньше или равен искомого
states = []
left = 0
right = len(a)
x = 14
while right - left > 1:
states.append(bs_state(a, left, right, x))
mid = (left + right) // 2
if a[mid] <= x:
left = mid
else:
right = mid
states.append(bs_state(a, left, right, x))
animate_list(states, play=True, interval=400);
Результат


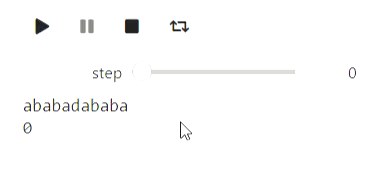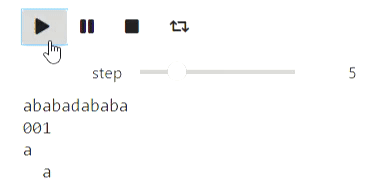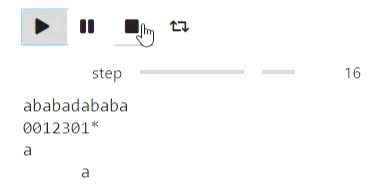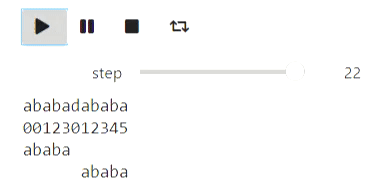
А вот пример для строк: процесс построения префикс-функции:
Код
def prefix_function_state(s, p, k, intermidiate=False):
third_string = ''.join([s[i] if i < k else ' ' for i in range(len(p))])
fourth_string = ''.join([s[i] if i >= len(p) - k else ' ' for i in range(len(p))])
return Code(s + '\n' + ''.join(list(map(str, (p + ['*'] if intermidiate else p )))) \
+ '\n' + third_string + '\n' + fourth_string)
def prefix_function(s, states):
p = [0]
k = 0
states.append(prefix_function_state(s, p, k))
for letter in s[1:]:
states.append(prefix_function_state(s, p, k, True))
while k > 0 and s[k] != letter:
k = p[k - 1]
states.append(prefix_function_state(s, p, k, True))
if s[k] == letter:
k += 1
p.append(k)
states.append(prefix_function_state(s, p, k))
return p
states = []
p = prefix_function('ababadababa', states)
animate_list(states, play=True);
Результат

Визуализация с использованием Matplotlib
Matplotlib — библиотека Python для отрисовки различных графиков. Вот несколько примеров как можно её использовать для визуализации алгоритмов. Начнем с примера итеративных алгоритмов поиска минимума функции, наиболее простым из которых является метод случайного локального поиска, которые делает локальное изменение тек��щего приближения и переходит в него если значение значение функции в новой точки оказалось лучше:
Код
import numpy as np
import matplotlib.pyplot as plt
# Функция, которую минимизируем, минимум в точке (0, 0)
def f(x, y):
return 1.3 * (x - y) ** 2 + 0.7 * (x + y) ** 2
# Отрисовка траектории и линий уровня функции
def plot_trajectory(func, traj, limit_point=None):
fig = plt.figure(figsize=(7, 7))
ax = fig.add_axes([0, 0, 1, 1])
if limit_point:
ax.plot([limit_point[0]], [limit_point[1]], 'o', color='green')
#Level contours
delta = 0.025
x = np.arange(-2, 2, delta)
y = np.arange(-2, 2, delta)
X, Y = np.meshgrid(x, y)
Z = np.zeros_like(X)
for i in range(X.shape[0]):
for j in range(X.shape[1]):
Z[i][j] = func(X[i][j], Y[i][j])
CS = ax.contour(X, Y, Z, [0.5, 1.5, 3], colors=['blue', 'purple', 'red'])
ax.plot([u[0] for u in traj], [u[1] for u in traj], color='black')
ax.plot([u[0] for u in traj], [u[1] for u in traj], 'o', color='black')
plt.close(fig)
return fig
x, y = (1.0, 1.0)
num_iters = 50
trajectory = [(x, y)]
plots = []
# Итерируемся и сохраняем текущий путь на каждом шаге
for i in range(num_iters):
angle = 2 * np.pi * np.random.rand(1)
dx, dy = (np.cos(angle) / 2 / (i + 1) ** 0.5, np.sin(angle) / 2 / (i + 1) ** 0.5)
trajectory.append((x + dx, y + dy))
plots.append(plot_trajectory(f, trajectory, limit_point=(0, 0)))
if f(x, y) > f(x + dx, y + dy):
x = x + dx
y = y + dy
else:
trajectory = trajectory[:-1]
animate_list(plots, play=True, interval=300);
Результат
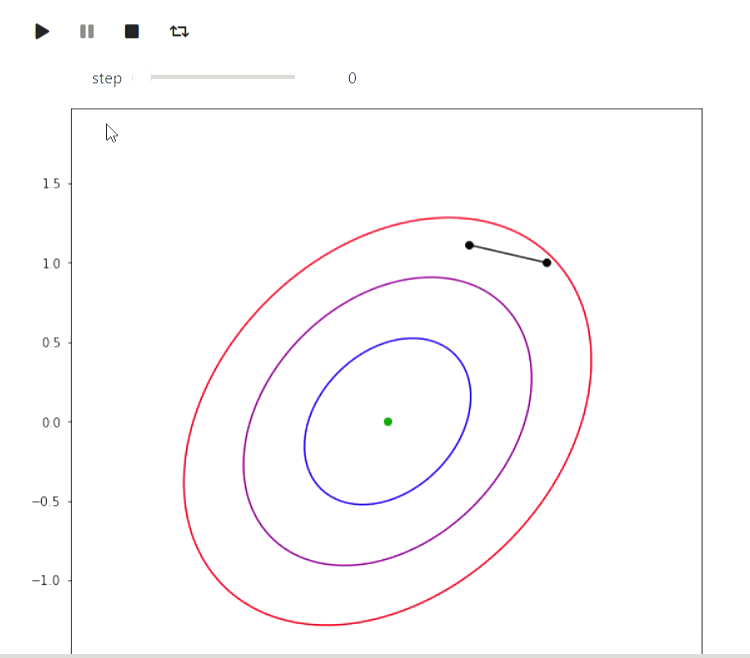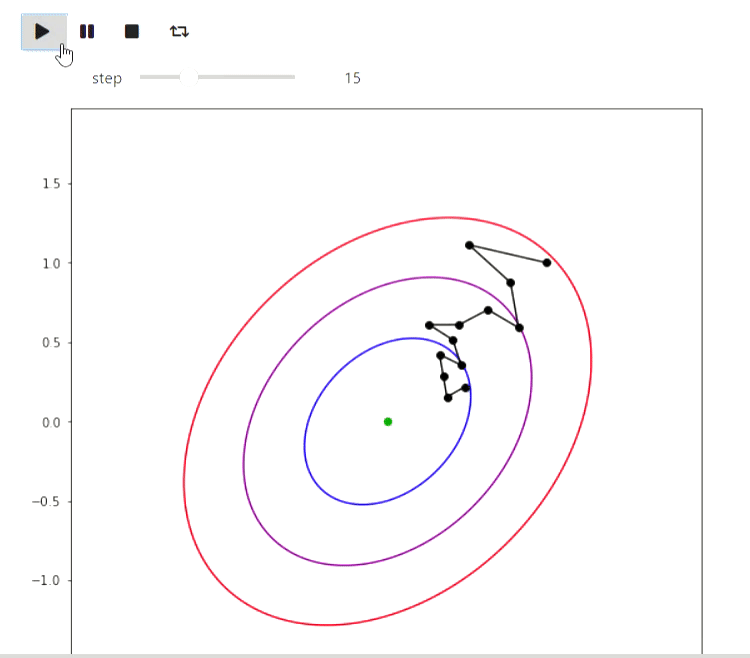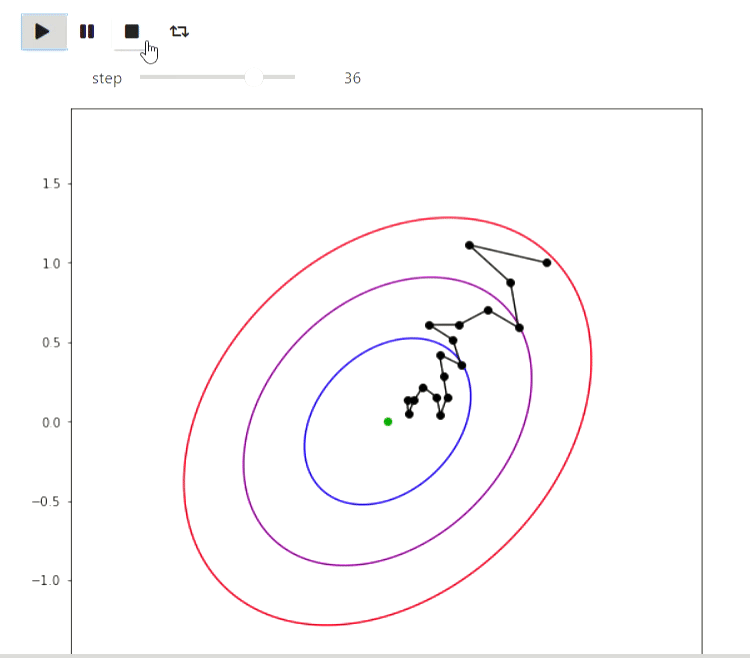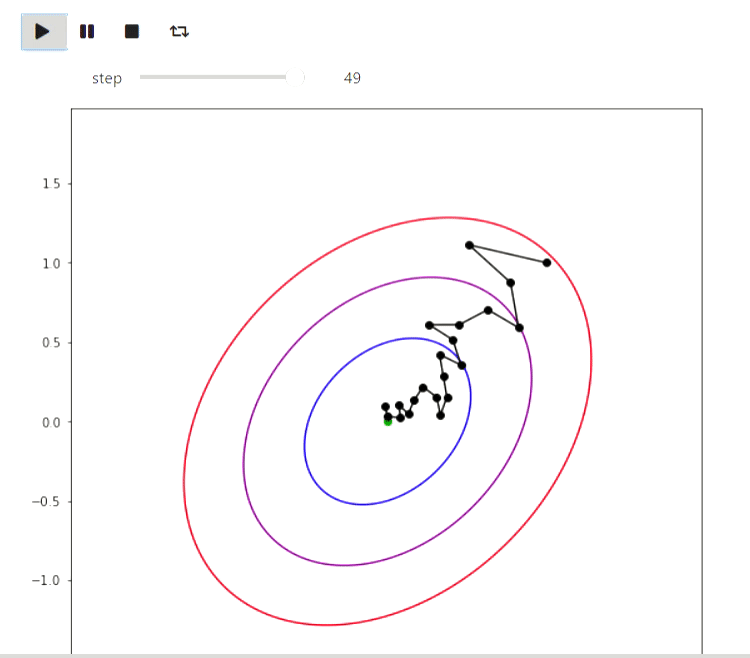

А вот пример ЕМ алгоритма для данных извержений Old Faithful гейзера, такой же пример приведен на википедии:
Код
# Данные можно взять например здесь
# http://www.stat.cmu.edu/~larry/all-of-statistics/=data/faithful.dat
data = []
with open('data/faithful.csv') as f:
for line in f:
_, x, y = line.split(',')
try:
data.append((float(x), float(y)))
except ValueError:
pass
colors = ['red', 'blue', 'yellow', 'green']
# За основу взято https://jakevdp.github.io/PythonDataScienceHandbook/05.12-gaussian-mixtures.html
from matplotlib.patches import Ellipse
def draw_ellipse(position, covariance, ax=None, **kwargs):
"""Draw an ellipse with a given position and covariance"""
ax = ax or plt.gca()
# Convert covariance to principal axes
if covariance.shape == (2, 2):
U, s, Vt = np.linalg.svd(covariance)
angle = np.degrees(np.arctan2(U[1, 0], U[0, 0]))
width, height = 2 * np.sqrt(s)
else:
angle = 0
width, height = 2 * np.sqrt(covariance)
# Draw the Ellipse
for nsig in range(1, 4):
ax.add_patch(Ellipse(position, nsig * width, nsig * height,
angle, color='red', **kwargs))
def plot_gmm(gmm, X, label=True, ax=None):
ax = ax or plt.gca()
if label:
labels = gmm.predict(X)
ax.scatter(X[:, 0], X[:, 1], c=labels, s=20, cmap='plasma', zorder=2)
else:
ax.scatter(X[:, 0], X[:, 1], s=20, zorder=2)
w_factor = 0.2 / gmm.weights_.max()
for pos, covar, w in zip(gmm.means_, gmm.covariances_, gmm.weights_):
draw_ellipse(pos, covar, alpha=w * w_factor)
def step_figure(gmm, X, label=True):
fig = plt.figure(figsize=(7, 7))
ax = fig.add_axes([0, 0, 1, 1])
ax.set_ylim(30, 100)
ax.set_xlim(1, 6)
plot_gmm(gmm, X, label=True, ax=ax)
plt.close(fig)
return fig
from sklearn.mixture import GaussianMixture
x = np.array(data)
# max_iters=1 и warm_start=True заставляют gmm.fit делать ровно одну итерацию
# и сохранять состояние
gmm = GaussianMixture(2, warm_start=True, init_params='random', max_iter=1)
# GMM выдает предупреждения на то, что одной итерации мало
import warnings
warnings.simplefilter('ignore')
# Инициализируем на небольшой порции данных
gmm.fit(x[:10,:])
steps = [step_figure(gmm, x)]
for i in range(17):
gmm.fit(x)
steps.append(step_figure(gmm, x))
animate_list(steps, play=True, interval=400);
Результат
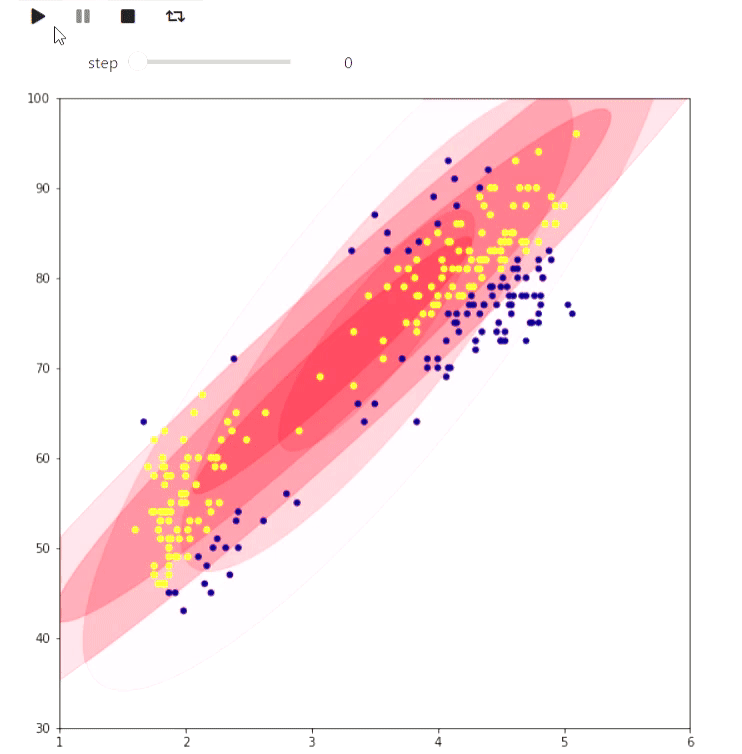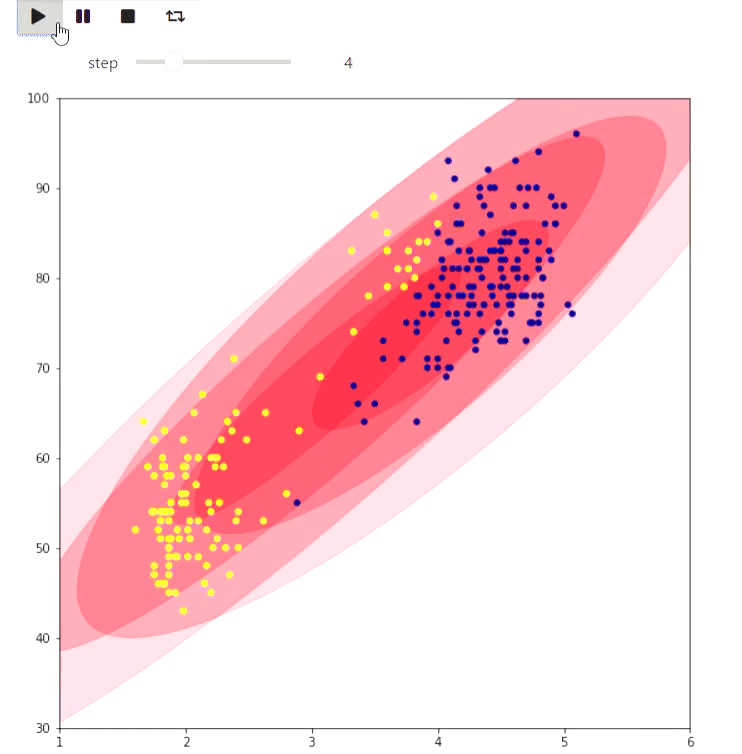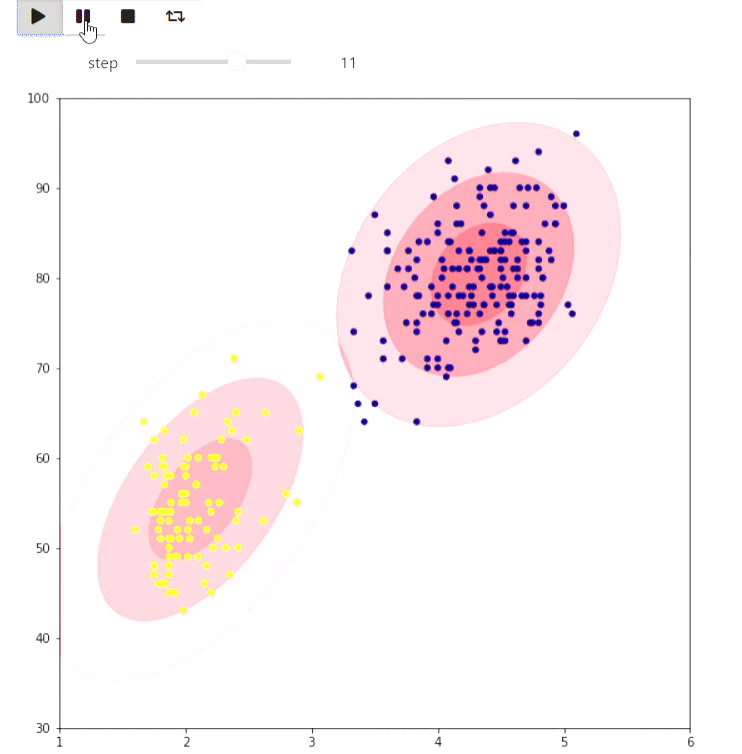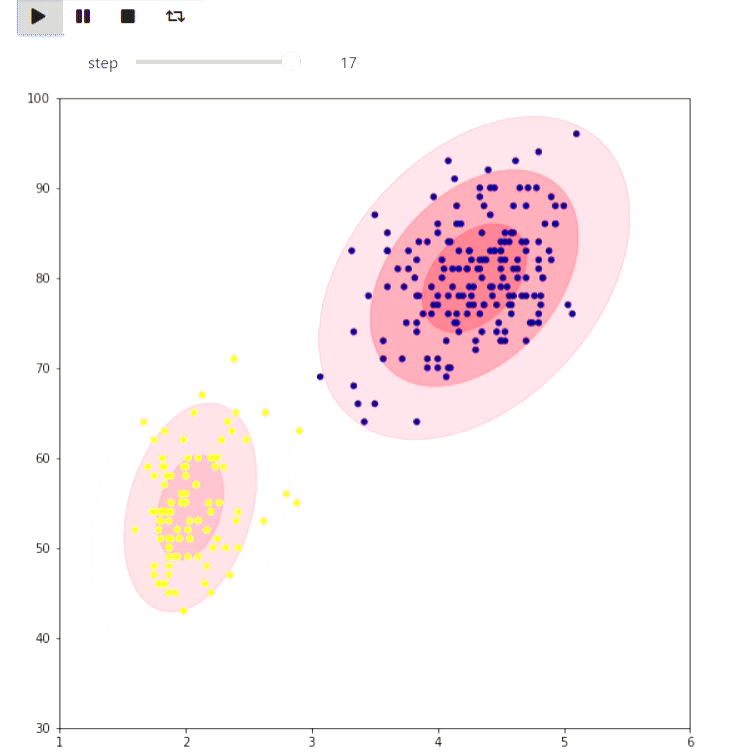

Следующий пример скорее игрушечный, но тоже показывает, что можно сделать в matplotlib: визуализация замощения клетчатой фигуры на плоскости максимальным числом доминошек с помощью нахождения максимального паросочетания:
Код
# Обертка над matplotlib для отрисовки прямоугольника, разделенного на квадраты разных цветов
from animation_utils.matplotlib import draw_filling
def check_valid(i, j, n, m, tiling):
return 0 <= i and i < n and 0 <= j and j < m and tiling[i][j] != '#'
def find_augmenting_path(x, y, n, m, visited, matched, tiling):
if not check_valid(x, y, n, m, tiling):
return False
if (x, y) in visited:
return False
visited.add((x, y))
for dx, dy in [(-1, 0), (1, 0), (0, -1), (0, 1)]:
if not check_valid(x + dx, y + dy, n, m, tiling):
continue
if (x + dx, y + dy) not in matched or find_augmenting_path(*matched[(x + dx , y + dy)], n, m, visited, matched, tiling):
matched[(x + dx, y + dy)] = (x, y)
return True
return False
def convert_match(matched, tiling, n, m):
result = [[-1 if tiling[i][j] == '#' else -2 for j in range(m)] for i in range(n)]
num = 0
for x, y in matched:
_x, _y = matched[(x, y)]
result[x][y] = num
result[_x][_y] = num
num += 1
return result
def match_with_flow(tiling):
result_slices = []
n = len(tiling)
m = len(tiling[0])
matched = dict()
# Для наглядности визуализации
rows = list(range(n))
columns = list(range(m))
random.shuffle(rows)
random.shuffle(columns)
result_slices.append(convert_match(matched, tiling, n, m))
for i in rows:
for j in columns:
if (i + j) % 2 == 1:
continue
visited = set()
if find_augmenting_path(i, j, n, m, visited, matched, tiling):
result_slices.append(convert_match(matched, tiling, n, m))
return result_slices
tiling_custom=[
'...####',
'....###',
'......#',
'#.#....',
'#......',
'##.....',
'###...#',
]
sequencial_match = match_with_flow(tiling_custom)
animate_list(list(map(draw_filling, sequencial_match)), play=True);
Результат


Ну и попутно демонстрация алгоритма раскраски планарного графа в 5 цветов, чтобы визуально разбиение смотрелось лучше:
Код
def color_5(filling):
result = [[i for i in row] for row in filling]
# Строим граф
domino_tiles = [[] for i in range(max(map(max, filling)) + 1)]
domino_neighbours = [set() for i in range(max(map(max, filling)) + 1)]
degree = [0 for i in range(max(map(max, filling)) + 1)]
n = len(filling)
m = len(filling[0])
for i, row in enumerate(filling):
for j, num in enumerate(row):
if num >= 0:
domino_tiles[num].append((i, j))
for i, tiles in enumerate(domino_tiles):
for x, y in tiles:
for dx, dy in [(-1, 0), (1, 0), (0, -1), (0, 1), (-1, -1), (-1, 1), (1, -1), (1, 1)]:
a, b = x + dx, y + dy
if 0 <= a and a < n and 0 <= b and b < m and filling[a][b] >= 0 and filling[a][b] != i \
and filling[a][b] not in domino_neighbours[i]:
domino_neighbours[i].add(filling[a][b])
degree[i] += 1
# Первым делом нужно найти такой порядок вершин, все вершины имели не больше 5 соседей среди
# предыдущих. Такой существует в силу того, что граф планарный, а найти его эффективнее всего
# по очереди находя вершину наименьшей степени и удаляя её из графа, так мы получаем обратный порядок
active_degrees = [set() for i in range(max(degree) + 1)]
for i, deg in enumerate(degree):
active_degrees[deg].add(i)
reversed_order = []
for step in range(len(domino_tiles)):
min_degree = min([i for i, dominoes in enumerate(active_degrees) if len(dominoes) > 0])
domino = active_degrees[min_degree].pop()
reversed_order.append(domino)
for other in domino_neighbours[domino]:
if other in active_degrees[degree[other]]:
active_degrees[degree[other]].remove(other)
degree[other] -= 1
active_degrees[degree[other]].add(other)
# Теперь перебираем в обратном порядке и либо красим в еще не занятый цвет,
# если есть свободный из 5 цветов, иначе находим цепочку из чередующихся цветов,
# которые могут быть перекрашены. Такая найдется в силу планарности
colors = [-1 for domino in domino_tiles]
slices = [draw_filling(result)]
for domino in reversed(reversed_order):
used_colors = [colors[other] for other in domino_neighbours[domino] if colors[other] != -1]
domino_color = len(used_colors)
for i, color in enumerate(sorted(set(used_colors))):
if i != color:
domino_color = i
break
if domino_color < 5:
colors[domino] = domino_color
for x, y in domino_tiles[domino]:
result[x][y] = domino_color
slices.append(draw_filling(result))
continue
# Начиная отсюда код я не тестировал, не нашел примера
c = 0
other = [other for other in domino_neighbours[domino] if colors[other] == c]
visited = set([other])
q = Queue()
q.put(other)
domino_was_reached = False
while not q.empty():
cur = q.get()
for other in domino_neighbours[cur]:
if other == domino:
domino_was_reached = True
break
if color[other] == c or color[other] == c + 1 and other not in visited:
visited.add(other)
q.put(other)
if not domino_was_reached:
for other in visited:
color[other] = color[other] ^ 1
for x, y in domino_tiles[other]:
result[x][y] = color[other]
color[domino] = c
for x, y in domino_tiles[domino]:
result[x][y] = c
slices.append(draw_filling(result))
continue
# Проделываем тоже самое для 2 и 3.
c = 2
other = [other for other in domino_neighbours[domino] if colors[other] == c]
visited = set([other])
q = Queue()
q.put(other)
domino_was_reached = False
while not q.empty():
cur = q.get()
for other in domino_neighbours[cur]:
if other == domino:
domino_was_reached = True
break
if color[other] == c or color[other] == c + 1 and other not in visited:
visited.add(other)
q.put(other)
for other in visited:
color[other] = color[other] ^ 1
for x, y in domino_tiles[other]:
result[x][y] = color[other]
color[domino] = c
for x, y in domino_tiles[domino]:
result[x][y] = c
slices.append(draw_filling(result))
return result, slices
filling_colored, slices =color_5(sequencial_match[-1])
animate_list(slices, play=True);
Результат


Последний пример с matplotlib из вычислительной геометрии — алгоритм Грэхэма-Эндрю для построения выпуклой оболочки на плоскости:
Код
def convex_hull_state(points, lower_path, upper_path):
fig = plt.figure(figsize=(6, 6))
ax = fig.add_axes([0, 0, 1, 1])
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
for name, spine in ax.spines.items():
spine.set_visible(False)
spine.set_visible(False)
ax.scatter([x for x, y in points], [y for x, y in points])
ax.plot([x for x, _ in lower_path], [y for _, y in lower_path], color='red')
ax.plot([x for x, _ in upper_path], [y for _, y in upper_path], color='blue')
plt.close(fig)
return fig
def vector_prod(point_a, point_b):
return point_a[0] * point_b[1] - point_a[1] * point_b[0]
def convex_hull(poitns):
sorted_points = sorted(points, key=lambda x: x[1])
sorted_points = sorted(sorted_points, key=lambda x: x[0])
states = []
upper_path = [sorted_points[0]]
lower_path = [sorted_points[0]]
states.append(convex_hull_state(points, lower_path, upper_path))
for point in sorted_points[1:]:
while len(upper_path) > 1 and vector_prod(point - upper_path[-1], upper_path[-1] - upper_path[-2]) > 0:
upper_path = upper_path[:-1]
upper_path.append(point)
states.append(convex_hull_state(poitns, lower_path, upper_path))
upper_path = upper_path[:-1]
upper_path.append(point)
states.append(convex_hull_state(points, lower_path, upper_path))
for point in sorted_points[1:]:
while len(lower_path) > 1 and vector_prod(point - lower_path[-1], lower_path[-1] - lower_path[-2]) < 0:
lower_path = lower_path[:-1]
lower_path.append(point)
states.append(convex_hull_state(poitns, lower_path, upper_path))
lower_path = lower_path[:-1]
lower_path.append(point)
states.append(convex_hull_state(poitns, lower_path, upper_path))
return states
points = [np.random.rand(2) for i in range(20)]
states = convex_hull(points)
animate_list(states, play=True, interval=300);
Результат


Последнее, что хотелось бы отметить в контексте matplotlib — это альтернативный способ создания анимаций через matplotlib.animation.FuncAnimation. У этого способа есть свои плюсы: его можно конвертировать в html с помощью IPython.display.HTML, результат будет более надежным, чем на виджетах (у меня виджеты периодически торомозят), не будет требовать рабочего ядра Jupyter, но в этом случае анимация стоновится обычным видео и средства управления ограничены проигрывателем.
Graphviz
С помощью graphviz можно отрисовывать графы. Обратите внимание, что для воспроизведения примеров с его помощью необходимо будет установить graphviz не только в python, но и в систему. Начнем с обхода в глубину:
Код
# Обертка для упрощения работы с графами
from graph_utils.graph import Graph, Arc, Node
def enter_node(node):
node.SetColor('blue')
def enter_arc(node, arc):
node.SetColor('green')
arc.attributes['style'] = 'dashed'
arc.attributes['color'] = 'green'
def return_from_arc(node, arc):
arc.attributes['style'] = 'solid'
arc.attributes['color'] = 'red'
node.SetColor('blue')
def ignore_arc(arc):
arc.attributes['color'] = 'blue'
def leave_node(node):
node.SetColor('red')
def dfs(graph, node_id, visited, outlist, path):
visited.add(node_id)
path.append(node_id)
enter_node(graph.nodes[node_id])
outlist.append(graph.Visualize())
for arc in graph.nodes[node_id].arcs:
if arc.end not in visited:
enter_arc(graph.nodes[node_id], arc)
dfs(graph, arc.end, visited, outlist, path)
return_from_arc(graph.nodes[node_id], arc)
path.append(node_id)
else:
ignore_arc(arc)
outlist.append(graph.Visualize())
leave_node(graph.nodes[node_id])
arcs = [
Arc(1, 3, 3),
Arc(1, 4, 7),
Arc(4, 3, 2),
Arc(4, 5, 3),
Arc(1, 5, 2),
Arc(6, 4, 2),
Arc(5, 6, 2),
Arc(6, 7, 1),
Arc(7, 2, 7),
Arc(4, 2, 2),
Arc(3, 2, 5)
]
# Если следующий код выдает ошибку, что ему не удается выполнить `dot`, то
# скорее всего придется отдельно поставить graphviz
# https://graphviz.org/download/
graph = Graph(arcs)
visited = set()
dfs_outlist = []
path = []
dfs_outlist.append(graph.Visualize())
dfs(graph, 1, visited, dfs_outlist, path)
dfs_outlist.append(graph.Visualize())
animate_list(dfs_outlist, play=True, interval=400);
Результат
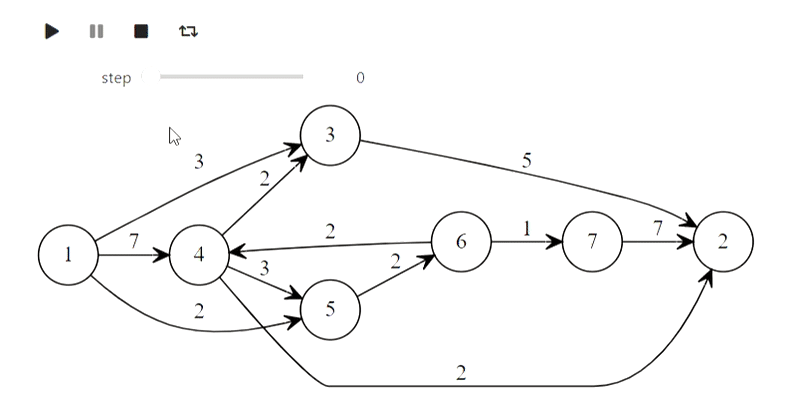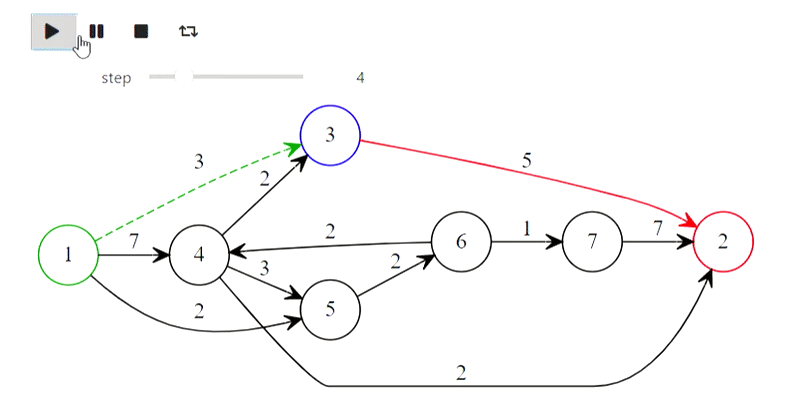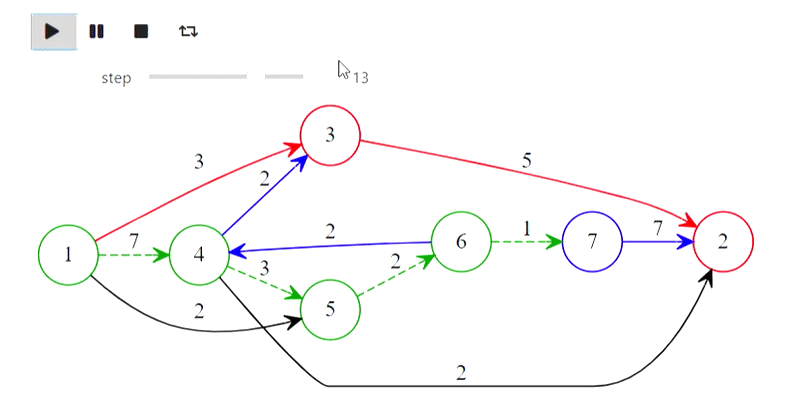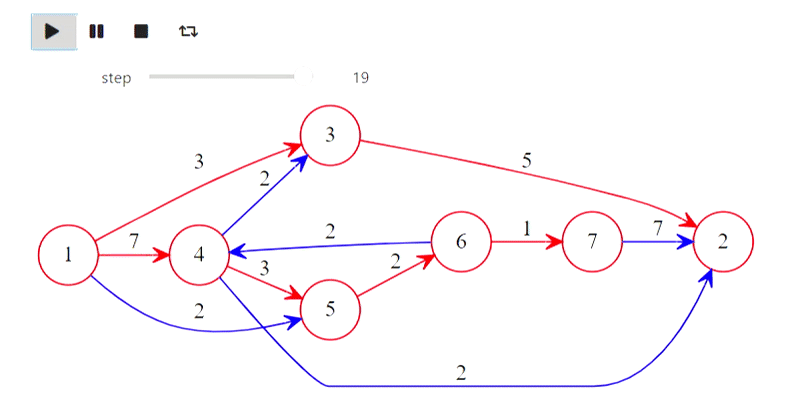

Ну а вот и алгоритм Дейкстры из заголовка
Код
def mark_labelled(node):
node.SetColor('red')
def mark_scanned(node):
node.SetColor('green')
def process_node(node):
node.SetColor('blue')
def set_previous(arc):
arc.SetColor('green')
def unset_previous(arc):
arc.SetColor('black')
def scan_arc(graph, arc, l, p, mark):
if l[arc.end] > l[arc.beginning] + arc.weight:
l[arc.end] = l[arc.beginning] + arc.weight
if p[arc.end] is not None:
unset_previous(p[arc.end])
# Сохраняем arc, а не arc.beginning, чтобы было больше информации
p[arc.end] = arc
set_previous(p[arc.end])
mark[arc.end] = True
mark_labelled(graph.nodes[arc.end])
def scan_node(graph, node_id, l, p, mark):
for arc in graph.nodes[node_id].arcs:
scan_arc(graph, arc, l, p, mark)
mark[node_id] = False
mark_scanned(graph.nodes[node_id])
# Это не традиционная реализация алгоритма Дейкстры, а реализация
# сканирующего метода, подробности смотрите тут
# http://forskning.diku.dk/PATH05/GoldbergSlides.pdf
def base_scanning_method(graph, s, choice_function):
l = {key: float('Inf') for key in graph.nodes.keys()}
p = {key: None for key in graph.nodes.keys()}
mark = {key: False for key in graph.nodes.keys()}
l[s] = 0
mark[s] = True
mark_labelled(graph.nodes[s])
out_lst = []
while True:
node_id = choice_function(l, mark)
if node_id is None:
break
process_node(graph.nodes[node_id])
out_lst.append(graph.Visualize(l))
scan_node(graph, node_id, l, p, mark)
out_lst.append(graph.Visualize(l))
return l, p, out_lst
# Функция выбора в алгоритме Дейкстры
def least_distance_choice(l, mark):
labelled = [node_id for node_id, value in mark.items() if value == True]
if len(labelled) == 0:
return None
return min(labelled, key=lambda x: l[x])
graph = Graph(arcs)
l, p, bfs_shortest_path_lst = \
base_scanning_method(graph, 1, least_distance_choice)
animate_list(bfs_shortest_path_lst, play=True, interval=400);
Результат


А вот таким образом происходит построение префиксного дерева для слов 'мама', 'мать', 'мартышка', 'мыла', 'молоко':
Код
class TrieNode:
def __init__(self, parent, word=None):
# Хранение этого поля очень расточительно, используется исключительно
# для демонстра��ии ленивого подсчета суффиксных ссылок
self.parent = parent
# Здесь аналогично, это поле чаще всего избыточно
self.word = word
self.children = {}
self.suff_link = None
def init_trie():
trie = [TrieNode(-1)]
return trie
def to_graph(trie):
arcs = []
for i, node in enumerate(trie):
for c, nextstate in node.children.items():
arcs.append(Arc(i, nextstate, c))
if node.suff_link is not None and node.suff_link != 0:
arcs.append(Arc(i,
node.suff_link,
attributes={"constraint" : "False", "style" : "dashed"}))
return Graph(arcs)
def add_word(trie, word, steps):
_num = 0
for ch in word:
if not ch in trie[_num].children:
_n = len(trie)
trie[_num].children[ch] = _n
trie.append(TrieNode((_num, ch)))
_num = trie[_num].children[ch]
graph = to_graph(trie)
graph.nodes[_num].SetColor('red')
steps.append(graph.Visualize())
trie[_num].word = word
def make_trie(words):
steps = []
trie = init_trie()
steps.append(to_graph(trie).Visualize())
for word in words:
add_word(trie, word, steps)
steps.append(to_graph(trie).Visualize())
return trie, steps
words = [
'мама',
'мать',
'мартышка',
'мыла',
'молоко'
]
trie, steps = make_trie(words)
animate_list(steps, play=True, interval=500);
Результат


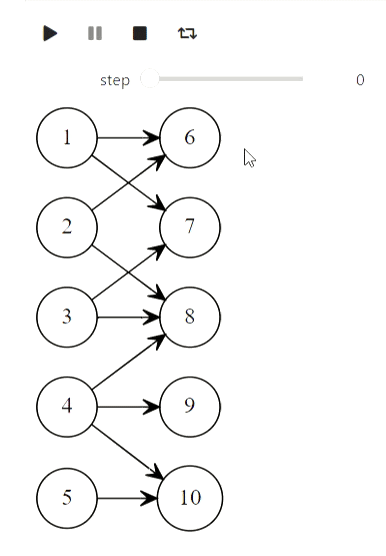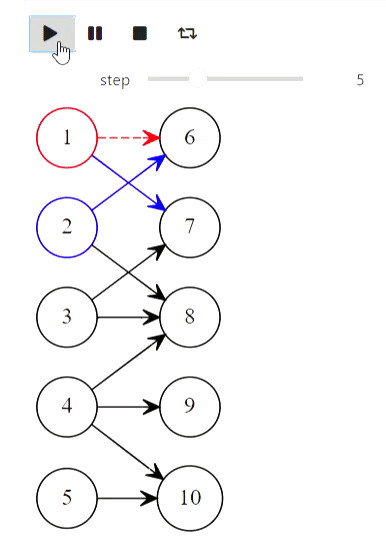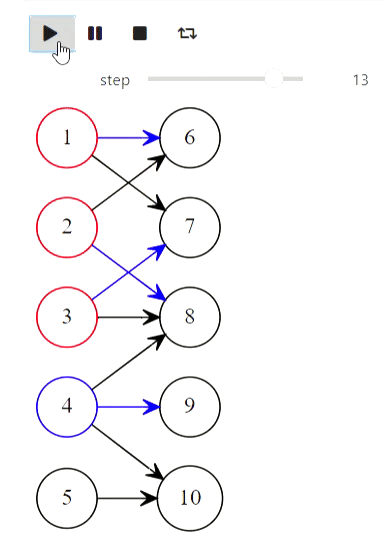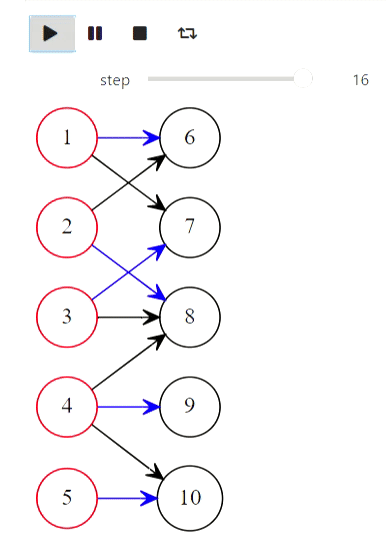
Ну и напоследок алгоритм Куна для нахождения максимального паросочетания:
Код
def mark_for_delete(arc):
arc.SetColor('red')
arc.SetStyle('dashed')
def mark_for_add(arc):
arc.SetColor('blue')
def clear(arc):
arc.SetColor('black')
arc.SetStyle('solid')
def find_augmenting_path(graph, node_id, visited, match, deleted):
if node_id in visited:
return False
visited.add(node_id)
for arc in graph.nodes[node_id].arcs:
if arc.end not in match or find_augmenting_path(graph, match[arc.end].beginning, visited, match, deleted):
if arc.end in match:
mark_for_delete(match[arc.end])
deleted.append(match[arc.end])
match[arc.end] = arc
mark_for_add(arc)
return True
return False
def kuhns_matching(graph, first_part):
states = [graph.Visualize()]
match = dict()
for node_id in first_part:
node = graph.nodes[node_id]
node.SetColor('Blue')
states.append(graph.Visualize())
deleted = []
if find_augmenting_path(graph, node_id, set(), match, deleted):
states.append(graph.Visualize())
for arc in deleted:
clear(arc)
states.append(graph.Visualize())
node.SetColor('red')
states.append(graph.Visualize())
return states
arcs = [
Arc(1, 6),
Arc(1, 7),
Arc(2, 6),
Arc(3, 7),
Arc(3, 8),
Arc(4, 8),
Arc(4, 9),
Arc(4, 10),
Arc(5, 10),
Arc(2, 8)
]
first_part = [1, 2, 3, 4, 5]
graph = Graph(arcs)
states = kuhns_matching(graph, first_part)
animate_list(states, play=True, interval=400);
Результат

Алгоритмы с матрицами
А вот эта часть относится к неудавшейся попытке. IPython.display умеет парсить latex, однако при попытки его использовать вот что у меня получилось (должен был быть метод Гаусса):
Код
from animation_utils.latex import Matrix
from IPython.display import Math
n = 5
A = np.random.rand(n, n)
L = np.identity(n)
U = np.array(A)
steps = []
steps.append(Math(str(Matrix(L)) + str(Matrix(U))))
for k in range(n):
x = U[k,k]
for i in range(k+1, n):
L[i,k] = U[i,k] / x
U[i,k:] -= L[i,k] * U[k,k:]
steps.append(Math(str(Matrix(L)) + str(Matrix(U))))
animate_list(steps, play=True, interval=500);
Результат
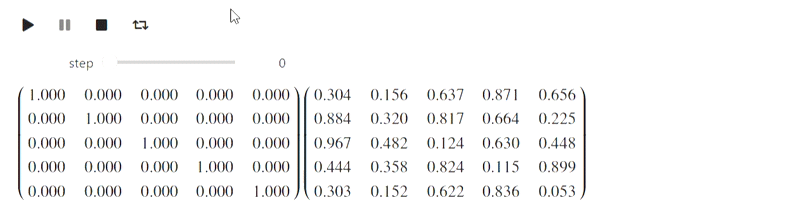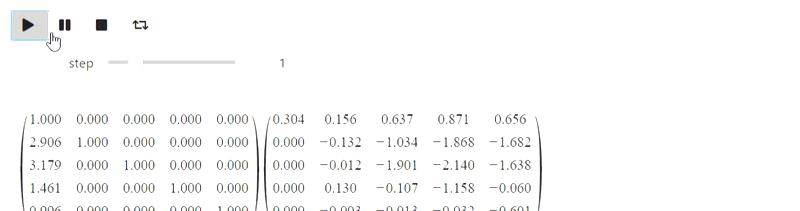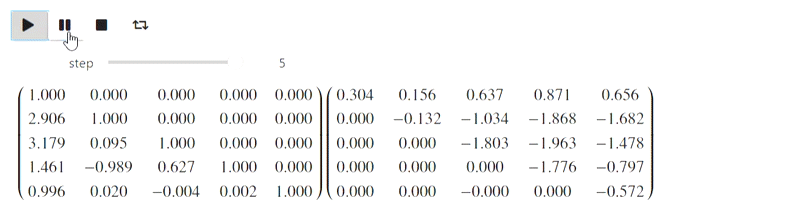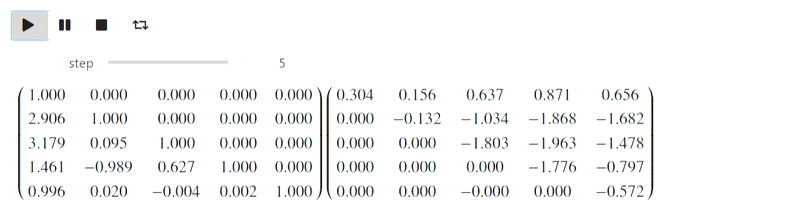

Пока я не знаю, что с этим делать, но возможно знающие люди подскажут.
