В этой части автор Александр Щекатуров, рассказывает основные принципы создания системы управления и ее моделирования в структурном виде. Всем кто одолел первые части лекций по теории управления в технических система, все будет ясно и понятно (ну почти). Лекции на хабре лежат по ссылкам:
- Введение в теорию автоматического управления.
- Математическое описание систем автоматического управления 2.1 — 2.3, 2.3 — 2.8, 2.9 — 2.13
В данной статье мы попробуем применить эти данные на практике. Используя модель, мы разберемся как воздействовать на коптер, что бы он летел в нужную нам сторону.
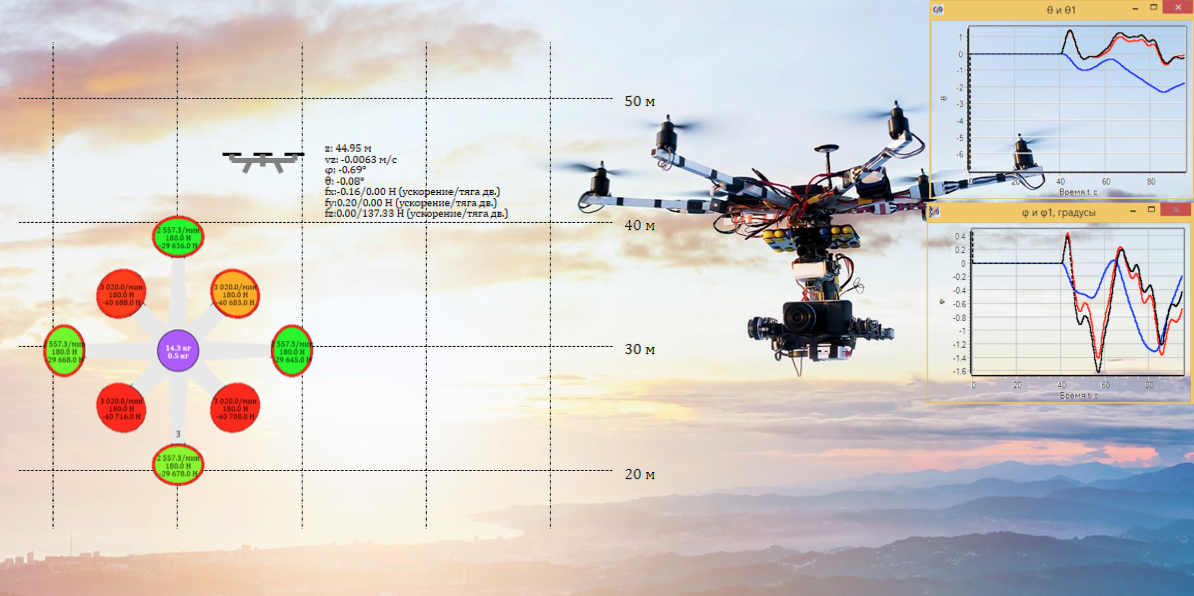
4 Управление моделью коптера
Всё что было описано в предыдущей части – это, по сути, формулировка «внутреннего» закона полета коптера – отвечающего на вопрос как именно объект будет менять свои ускорения, скорости и координаты в зависимости от приложенных сил и моментов. Т.е. мы записали уравнение F(t) = ma(t) (и аналогичное для суммарного момента и углового ускорения) для октокоптера заданной геометрической конструкции. В эти уравнения входят некоторые константы – масса коптера, его моменты инерции по главным осям (составляющие тензора инерции), угол отклонения силы тяги ВМГ от вертикали, длины лучей рамы коптера, и некоторые другие массогабаритные характеристики. Как правило, это константы, за редким исключением. Но т.к. задача поставлена в общем виде, мы не подставили ещё конкретных чисел, а все эти величины заменили на символы (символьные константы и/или переменные), и теперь требуется их задать числами для работоспособности модели. Для двигателей это будет коэффициент пропорциональности между квадратом угловой скорости и силой тяги, для массы коптера – масса рамы плюс массы всех ВМГ и т.д.
4.1 Переменные проекта — сигналы модели
В SimInTech используется плоский неструктурированный список сигналов, и/или структурированная (объектно-ориентированная) база сигналов для задания констант и переменных модели, если в ней есть типовые (повторяющиеся) элементы. В данной модели были и тем и другим способом заведены следующие сигналы (переменные и константы), см. рисунки 13 и 14:
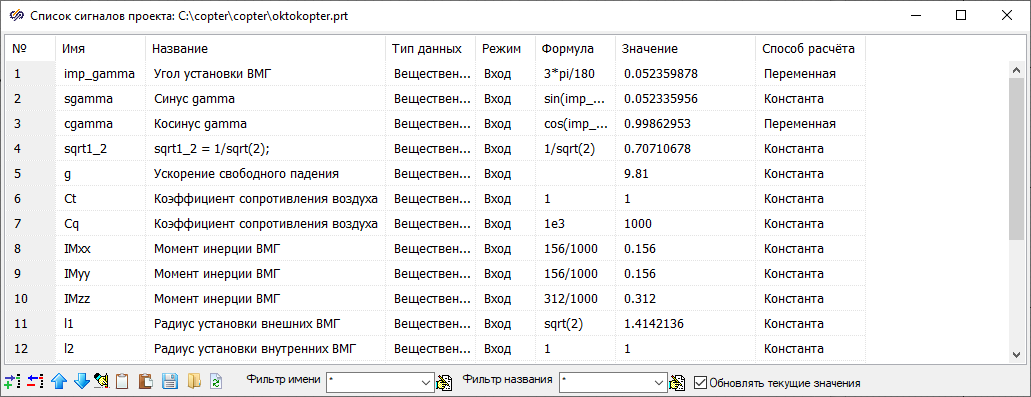
Рисунок 13. Сигналы проекта
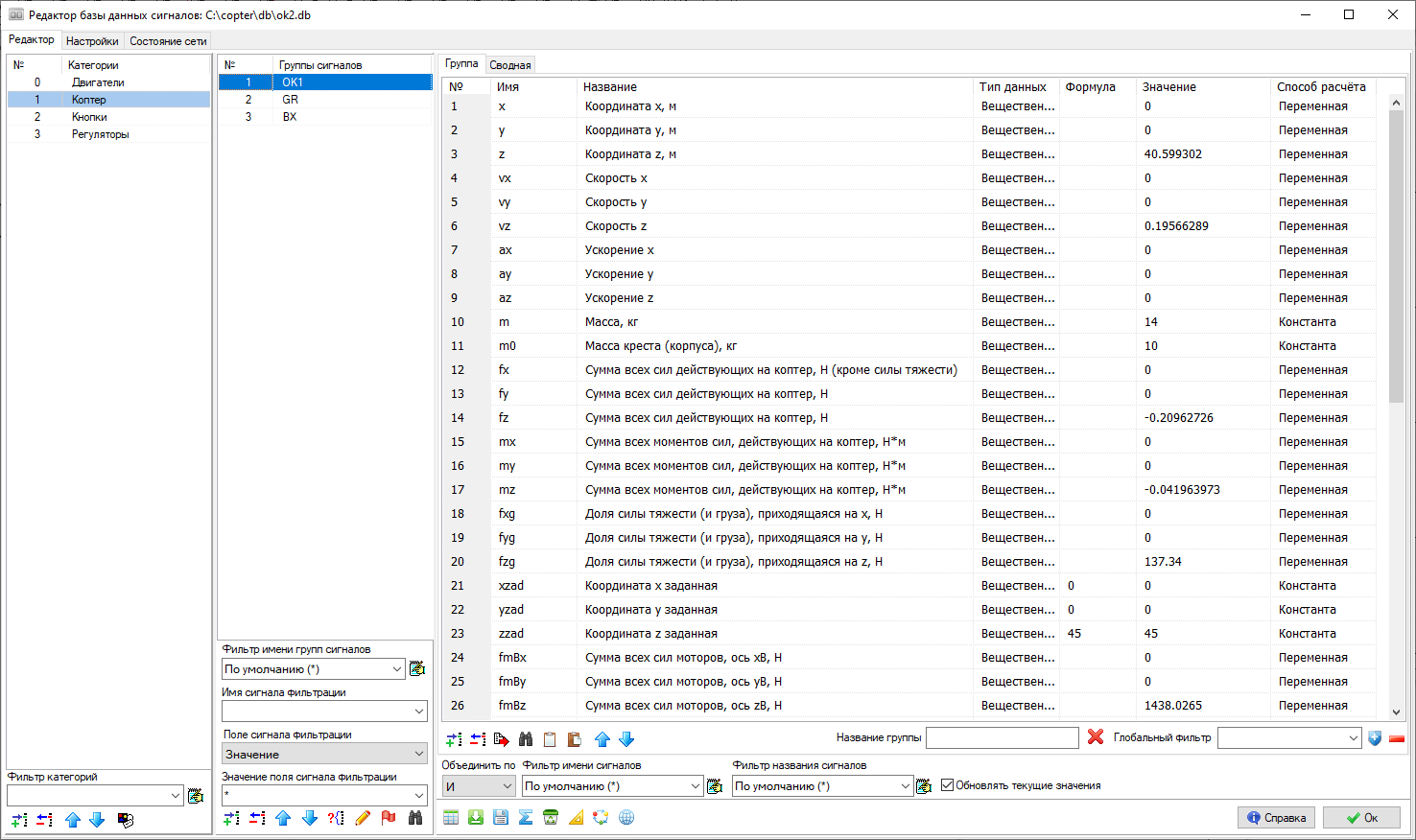
Рисунок 14. База сигналов проекта
Среди повторяющихся элементов в коптере явно можно выделить ВМГ – они все однотипны и параметризуются одинаковыми (по смыслу) переменными. Также, для регуляторов, которых будет всего 6 (по числу каналов регулирования) – тоже можно выделить однотипные элементы. Если это будут ПИД-регуляторы, то коэффициенты пропорциональности P, I, D будут в наличии у каждого из регуляторов, со своим конкретным значением.
Таким образом, в одном месте в структурированном виде собраны все константы (параметризующие модель) и переменные, используемые для вычислений. В дальнейшем их легко можно забирать отсюда, из базы сигналов, и использовать в других частях модели. При необходимости вносить в модель корректировки констант – это тоже удобно делать когда они все сведены в одном месте модели, а не разбросаны в разных местах.
Рассмотрим немного подробнее параметризацию двигателей (см. рисунок 15). Всего в базе 8 групп сигналов, по 15 сигналов в каждой – то есть 120 переменных и констант, описывающих состояние всех двигателей. Важными и задаваемыми пользователем (разработчиком модели) являются wnom, wmin – номинальная и минимальная частоты вращения. В дальнейшем эти значения используются в модели двигателя, ограничивая «снизу» текущую частоту вращения, и для расчета текущих оборотов ВМГ в единицах измерения. Остальные переменные – расчитываются в модели и зависят от времени. В эту же категорию можно в дальнейшем добавить и коэффициенты пропорциональности между квадратом угловой скорости и силой тяги ВМГ.
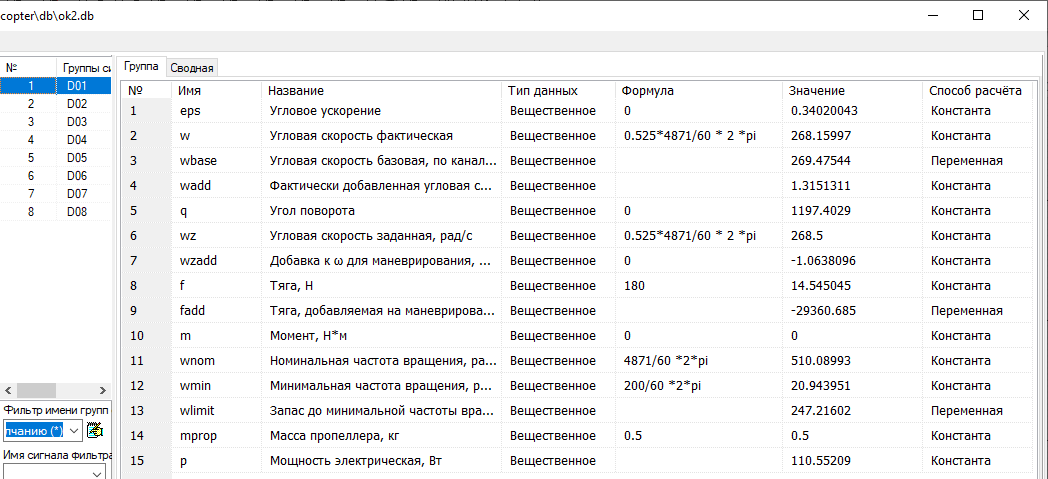
Рисунок 15. Категория «Двигатели»
4.2 Оптимальное управление
С точки зрения управления коптер представляет собой не самую простую конструкцию – мы имеем 8 двигателей, которыми можно управлять индивидуально, но практически каждый из них влияет на все 12 из переменных состояния (фазовых координат) коптера. То есть, если мы будем «рулить» одним из двигателей – менять его обороты в большую или меньшую сторону, это будет оказывать воздействие на каждую из координат x, y, z и на каждую из трёх угловых скоростей. Кроме случаев, когда вектор тяги параллелен какой-либо из координатных плоскостей системы B – тогда на 4 из 12 переменных состояния данная сила тяги воздействовать не будет. И, если бы мы делали всё методами классической теории управления, то можно было бы записать 8х12 = 96 передаточных функций между 8 входными воздействиями и 12 выходными (переменными состояния) коптера.
Также, изменение оборотов (частоты вращения) двигателей приводит к нелинейному (а к квадратичному) изменению силы тяги. В проектировании регуляторов коптера это предполагается как аксиома, и она довольно хорошо согласуется с экспериментальными данными.
Задача оптимального управления заключается в том, чтобы перевести коптер из точки А в точку Б с минимальным перерегулированием, по оптимальной (как правило кратчайшей) траектории и за минимальное время. При этом налагаются ограничения на максимальную скорость, ускорения и углы наклона коптера (отклонение от горизонтальности). Проблема заключается в том, что в «прямую» сторону можно довольно несложно посчитать – как воздействует каждый из двигателей (8 переменных – 8 частот вращения) на каждую из 12 переменных состояния. А если учитывать еще и ускорения, то на каждую из 18 переменных. Но в задаче управления требуется наоборот – при заданных начальных и конечных координатах требуется вычислить как именно надо управлять двигателями чтобы коптер перешел из одного состояния в другое.
Если не сильно вдаваться в теоретические дебри теории оптимального управления и нелинейного программирования, такую задачу можно свести и решить методом множителей Лагранжа, а точнее – условиями и методом Каруша-Куна-Такера, где ограничения, накладываемые на переменные, представляют собой неравенства.
Чтобы упростить изложение, приведем краткий ход решения задачи. Для начала запишем матрицу Г размерностью 6х8 – по количеству каналов управления (6) и количеству ВМГ (8), которая будет отображать как именно каждый из двигателей влияет на каждый из каналов управления:
Где: fi|x,y,z – это коэффициент перед для вычисления силы, которую создаёт i-ая ВМГ в соответствующем направлении, а mi|x,y,z – коэффициент перед
для вычисления момента сил, который создаёт i-ая ВМГ в том же направлении:
Примечание: если у ВМГ будет еще реактивный момент, то у будет еще одно слагаемое.
Легко видеть, что матрица Г показывает зависимость между квадратом угловой скорости i-ой ВМГ и управляющими (силовыми) воздействиями по каждому из каналов управления: . Нам же нужно получить обратное решение – зависимость угловой скорости i-ого двигателя от поданного управляющего воздействия по какому-либо из каналов управления. В общем виде эта задача имеет бесконечное множество решений, однако среди этого бесконечного множества можно выделить по тому или иному критерию или способу оптимальное решение.
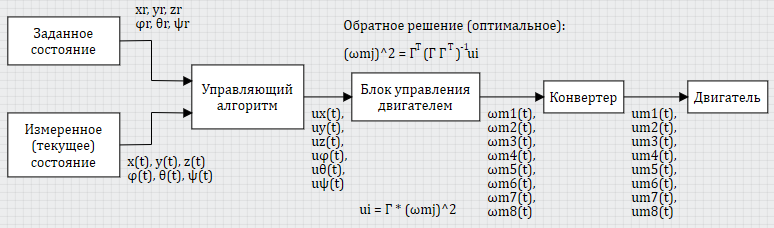
Рисунок 16. Структура регулятора
Методами теории оптимального управления (подробнее см. [1, раздел 4.1.1]) задача решается поиском так называемой обратной псевдоинверсной матрицы , которая вычисляется как:
. Она же и является оптимальным решением поставленной задачи с наложенными ограничениями на решение.
На практике, для заданной геометрии коптера и полученных 48 чисел в матрице Г, получаем другие 48 чисел, которые определяют правило управления (микширования) двигателей, при поступлении той или иной команды по какому-либо каналу управления. На рисунке 16 представлена общая схема построения регулятора. Задатчик положения вырабатывает нужные координаты, в которые требуется привести коптер. Они сравниваются по какому-то алгоритму с измеренными координатами и управляющий алгоритм вырабатывает 6 управляющих воздействий, по каждому из каналов управления.
На основе посчитанной псевдообратной матрицы , блок управления двигателями вычисляет текущие заданные значения угловых скоростей для каждого из 8 двигателей, как бы суммируя пришедшие 6 команд по каналам управления и определенным образом микшируя двигатели при этом. Сформированные 8 угловых скоростей отправляются на задатчик оборотов двигателей и осуществляется регулирование и управление коптером (см. рисунок 16).
Управляющие команды по каждому из каналов управления формируются как рассогласование между заданной координатой (углом) и текущей, измеренной координатой. Это в самом простом варианте. В более сложном управляющий алгоритм должен иметь в своём составе алгоритм приоритетности стабилизации положения коптера над алгоритмом перемещения в пространстве. Дело в том, что по каждому из каналов есть запас (располагаемая у ВМГ возможность) управления. И, если (например) мы сделаем приоритетным перемещение по оси х то при большом рассогласовании между текущей координатой x и заданной регулятор будет стремиться наклонить всё больше и больше коптер вокруг оси y, и при определенном наклоне уже не х��атит возможностей двигателей обеспечивать стабилизацию коптера и регулирование высоты полёта. Для коптера с конкретными параметрами двигателей, винтов, массы и размеров это всё можно вычислить и наложить нужные ограничения на управляющие воздействия ui(t), а также их приоритет. Но это выходит за рамки данной статьи, где мы делаем модель в общем виде. Просто отметим, что стабилизация положения для коптера – самая важная задача, перемещение – уже вторична, поскольку без стабильного положения переместиться куда-либо целенаправленно будет невозможно.
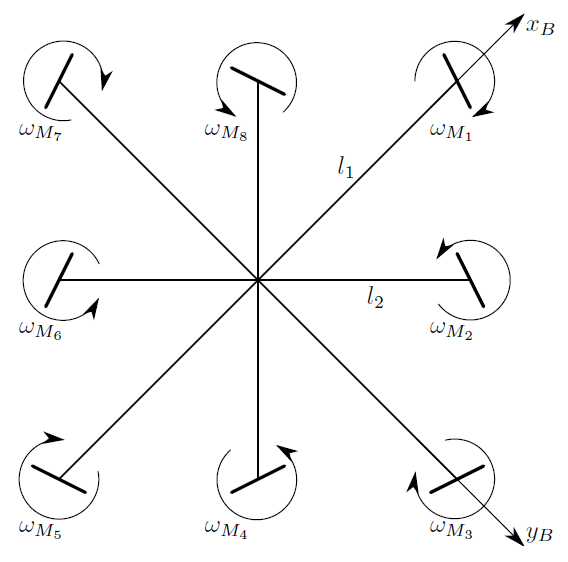
Выпишем аналитические выражения для элементов первых двух столбцов матрицы Г в случае рассматриваемого октокоптера (без реактивного момента ВМГ и без прецессии!):
Видно, что первая ВМГ (ось силы тяги которой параллельна плоскости yz) не создаёт никакой силы вдоль оси x и никакого момента вокруг оси x (т.к. пересекает её). Поэтому при управлении по оси x или для создания вращательного момента вокруг оси x первый двигатель «бесполезен». Аналогично будет с 5-ым двигателем, а для 3-его и 7-ого будет такая же картина для оси y (всё справедливо в системе координат В).
Аналитические выражения для матрицы будут гораздо более громоздкими и большого смысла не имеют – проще вычислить численно матрицу Г, а потом и искомую
. В нашем случае для одного из вариантов октокоптера, она получилась равной:
Смысл матрицы примерно в следующем: она показывает на какое количество надо изменить частоту вращения каждой i-ой ВМГ (из 8), чтобы осуществить единичное управляющее воздействие на объект по тому или иному каналу управления. Например, если мы хотим к коптеру приложить силу 1 Н по каналу управления x (первая колонка), то угловую скорость 1-го двигателя и 5-го менять не надо, а к текущим угловым скоростям других двигателей надо добавить или отнять примерно 13,8 рад/с. Это довольно приличное изменение угловой скорости, и вообще управляемость по каналам x, y появилась здесь как побочное следствие того, что каждая из ВМГ повёрнута вокруг своего луча еще на 3 градуса.
Если бы все ВМГ были расположены вертикально, то первые две колонки матрицы получились бы бесконечными – т.е. коптер с вертикально расположенными ВМГ по горизонтальным осям не управляется вообще! Управление по этим осям (в инерциальном пространстве) достигается поворотом коптера вокруг осей и перенаправлением суммарного вектора тяги в какую-либо сторону.
Третья колонка – управление по оси z, имеет отрицательные числа т.к. ось z направлена вниз, а вектора силы тяги ВМГ – вверх. Обратим внимание, что абсолютные значения чисел третьей колонки гораздо меньше, чем первой и второй и все имеют один и тот же знак. Это означает что коптер имеет гораздо лучшую управляемость по вертикальной оси, что очевидно, т.к. все ВМГ как раз и работают практически в эту сторону (а не влево-вправо-вперёд-назад). Четвёртая колонка и пятая – это управляемость коптера по крену и тангажу, последняя шестая – по курсу. Видно, что по курсу коптер гораздо слабее управляем, чем по крену и тангажу. Но для наших целей, и для целей настоящей обучающей статьи, этого было достаточно. Подбором направлений сил тяги ВМГ (и перевычислением матриц для новой геометрии) можно этот баланс менять.
Обратим также внимание на то, что теоретически – при вычисленном и приведенном здесь количественно микшировании двигателей, достигается только управление по выбранному каналу, без влияния на другие каналы управления. Т.е. при выбранном расположении ВМГ у октокоптера, в некоторых малых пределах можно изменять направление вектора тяги, без создания поворотных моментов т.е. не наклоняя сам коптер, и он будет горизонтально лететь и управляться без наклонов. Но только в очень узком диапазоне скоростей и внешних возмущений.
Общая структура регулятора приведена на рисунках 17 и 18.
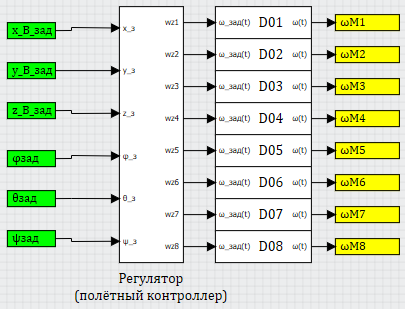
Рисунок 17. Общая схема регулятора
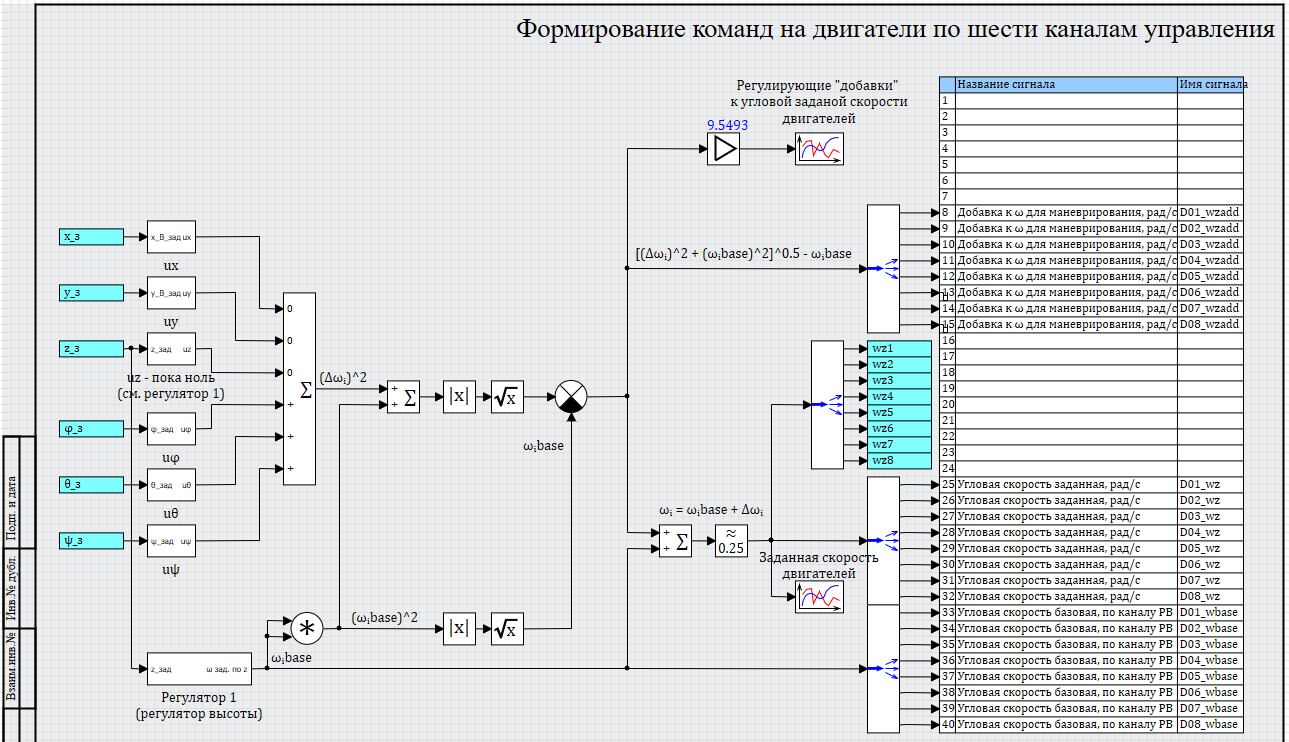
Рисунок 18. Схема каналов регулятора
В самом простейшем случае — на 6 входов регулятора поступают заданные фазовые координаты, они сравниваются с текущими (измеренными) и в общем случае в соответствии с матрицей и ПИД-регулированием по каждому из каналов, вырабатывается 6 управляющих векторов, по 8 переменных в каждом, которые суммируются и получаем итоговый вектор управления с заданными угловыми скоростями для каждого из двигателей. На практике, не всё так просто…
4.3 Регулятор высоты
Регулятор высоты можно выделить отдельно от других, поскольку он задействует примерно одинаково все двигатели, и даже без матриц Г и понятно: для того чтобы коптер летел вверх, надо увеличивать газ, а чтобы вниз – уменьшать обороты ВМГ. В качестве простейшего регулятора высоты можно взять обычный ПИД-регулятор, который справится с управлением при верно подобранных коэффициентах. На рисунке 19 показан один из вариантов регулятора, с доработкой ограничения вертикальной скорости, если текущая позиция отличается от заданной более чем на 5 метров.
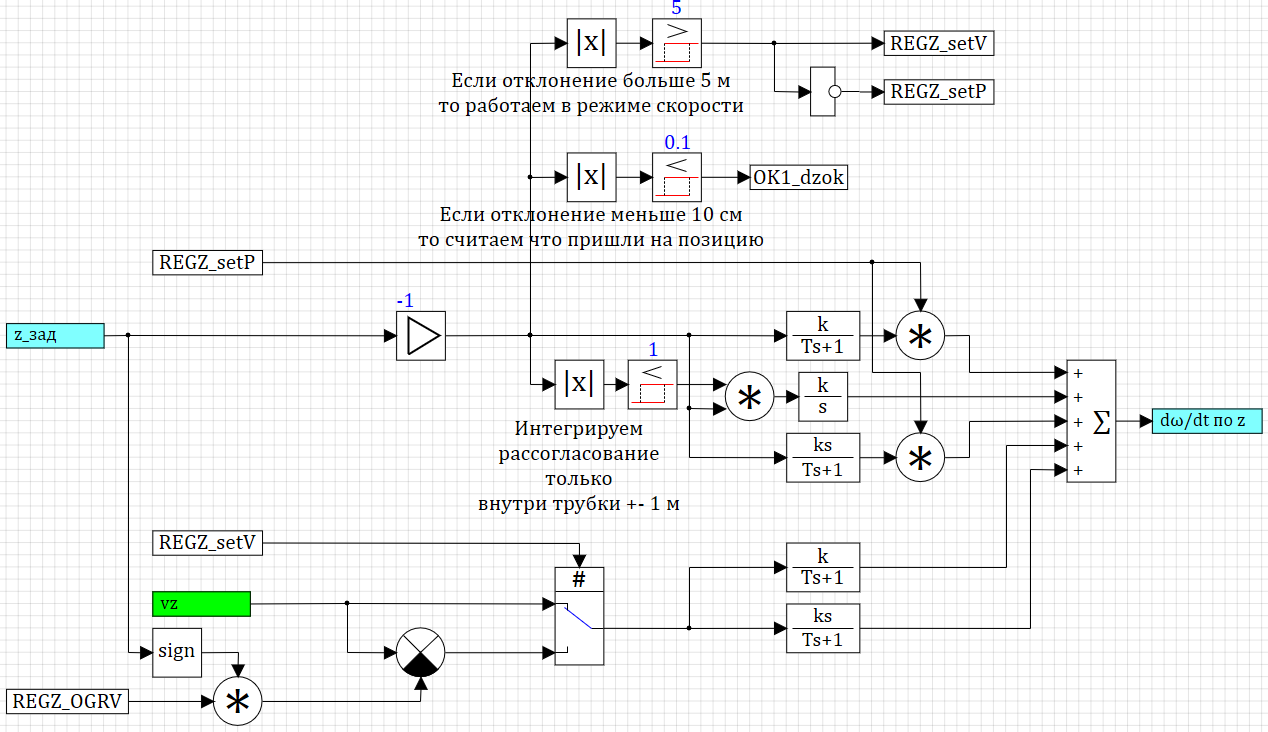
Рисунок 18. Регулятор высоты, один из вариантов
В чем основная идея регулятора: на вход подается текущая величина рассогласования между заданной высотой и измеренной высотой, подаётся текущая вертикальная скорость и ограничение на вертикальную скорость. Если рассогласование больше 5 метров, то регулятор работает в режиме ограничения скорости и стремится к тому, чтобы вертикальная скорость vz стала равной +OGRV м/с или -OGRV м/с в зависимости от направления полёта. Если рассогласование менее 5 м, то регулятор стремится к нулевой скорости полёта и сведению в ноль рассогласования по высоте.
Выходной сигнал регулятора подается с коэффициентами матрицы (согласно третьей колонке) на каждый из 8 двигателей.
4.4 Регулятор ориентации коптера
Углы φ крена и θ тангажа являются одними из самых важных для коптера т.к. отвечают за стабилизацию его положения в пространстве, и должны иметь самый высший приоритет среди других каналов управления. Поскольку коптер симметричен, то регуляторы с точностью до осей симметрии похожи друг на друга.
В стабильном состоянии по каждой из осей и
угол наклона должен быть нулевым, угловая скорость должна быть нулевой, и приложенный момент сил тоже должен быть нулевым. Регулятор ориентации должен быть достаточно быстродействующим чтобы успевать парировать внешние возмущающие моменты и не давать коптеру сильно отклоняться от нулевой позиции, т.к. любой наклон коптера приводит к уменьшению вертикальной составляющей силы тяги и к уводу коптера в соответствующую сторону вбок.
Для сведения к нулю трёх составляющих – угла, скорости и момента – они должны быть входными сигналами в регулятор. Один из вариантов представлен на рисунке 19. Заданное значение равно нулю, и в стабильном состоянии выходной сигнал сумматора будет равен нулю. Если появляется какое-то ненулевой состояние, то выход регулятора будет также отличен от нуля, далее он домножается на вектор, равный 4-ой колонке псевдообратной матрицы , представленной выше и формируется вектор усилий на 8 ВМГ, который должен компенсировать возникший дисбаланс поворота вокруг оси
.
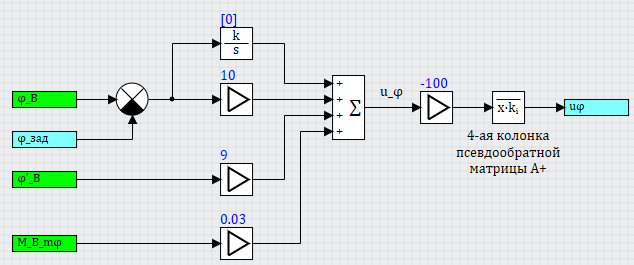
Рисунок 19. Регулятор крена
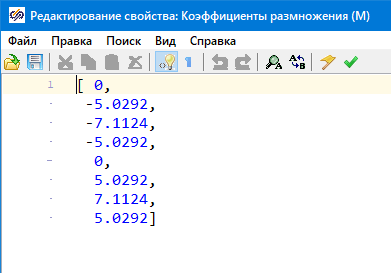
Рисунок 20. Коэффициенты блока типа «Размножитель» в регуляторе крена
Аналогично выполнен и регулятор по каналу тангажа (представлен на рисунке 21).
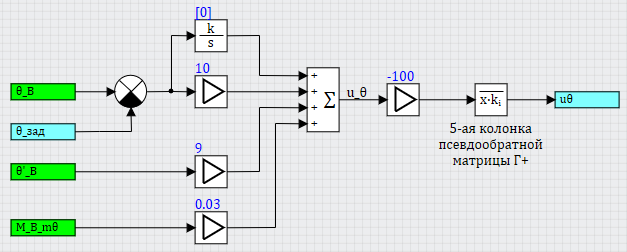
Рисунок 21. Регулятор тангажа
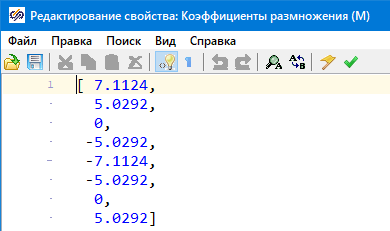
Рисунок 22. Коэффициенты блока типа «Размножитель» в регуляторе тангажа
Конкретные значения на линиях регулятора, пропорциональных углу, угловой скорости и угловому ускорению (моменту сил) подбираются численным экспериментом для данного коптера (с конкретными массой, моментами инерции по осям, двигателями, размером рамы и т.д.).
4.5 Регулятор положения коптера в пространстве
Итого, регулятор ориентации коптера и регулятор высоты, работая совместно, обеспечивают «висение» коптера в определённой точке пространства в состоянии динамического равновесия. При этом, у коптера еще остается некоторый запас управляемости, который позволяет ему двигаться целенаправленно вдоль координатных осей. Но данные регуляторы несколько сложнее чем регулятор ориентации.
Во-первых, они работают в системе координат В, а в общем случае коптер вращается в пространстве (по курсу) и направления осей x и y системы В не совпадают с такими же осями в системе I. Поэтому рассогласование его позиции в системе I надо переводить в систему В и дополнительно подготавливать задание на регулятор положения по осям x и y.
Во-вторых, рассогласование в этом регуляторе может быть как небольшим, так и значительным, а обычный ПИД-регулятор, как правило, не может одинаково эффективно работать с малыми и с большими отклонениями, требуется доработка регулятора – например, переключение регулятора положения в режим поддержания постоянной скорости при каких-то условиях.
В-третьих, у классического коптера с винтами, расположенными в одной плоскости и параллельными силами тяги, направленными вверх, практически нет возможности создавать боковую силу тяги – т.е. по существу, коптер является неуправляемым по осям X и Y. В нашем варианте, когда винты довернуты еще на 3 градуса вокруг своих лучей, у них появляется небольшая сила тяги направленная в стороны, и микшированием двигателей можно создавать боковую силу тяги. Однако, она очень несущественна, почти нулевая – об этом свидетельствуют большие числа в 1 и 2 колонках матрицы — для того, чтобы создать силу тяги величиной 1Н в сторону, нужно изменить частоту вращения двигателей почти на 15 рад/с (квадрат частоты вращения – на 191 (1/с)2). С точки зрения управления, это слишком большая величина. Поэтому коптеры управляются по направлениям X и Y при помощи других каналов управления – поворачиваясь вокруг осей X и Y (об этом напишем дальше).
Но структурно – если делать регулятор по каналам Х и Y типовым образом, регулятор может быть выполнен аналогично регуляторам ориентации – на выходе формируется управляющее воздействие по каналу X (Y) и домножается на вектор – 1 (или 2) колонку матрицы , а полученные 8 сигналов п��даются на ВМГ.
Один из вариантов регулятора по каналу X и Y представлены на рисунке 23 и 24.
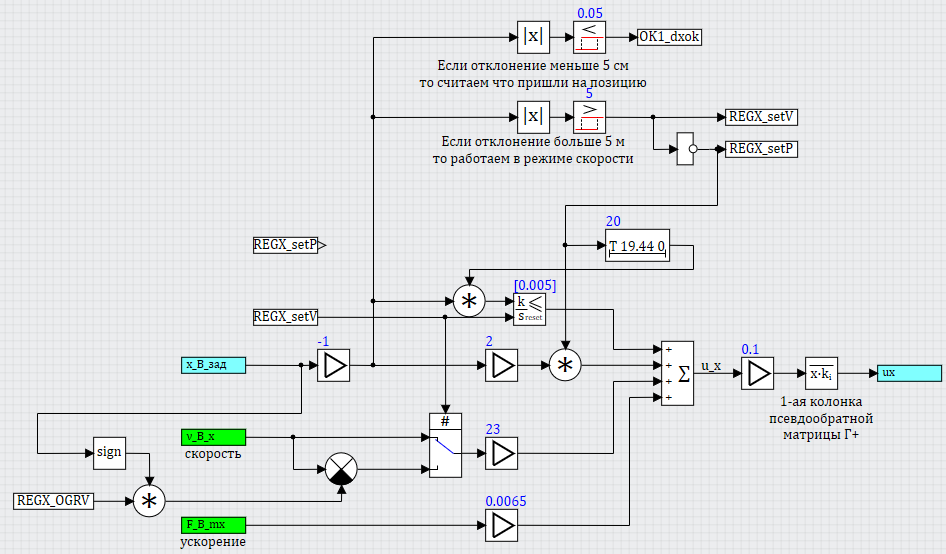
Рисунок 23. Регулятор по каналу Х
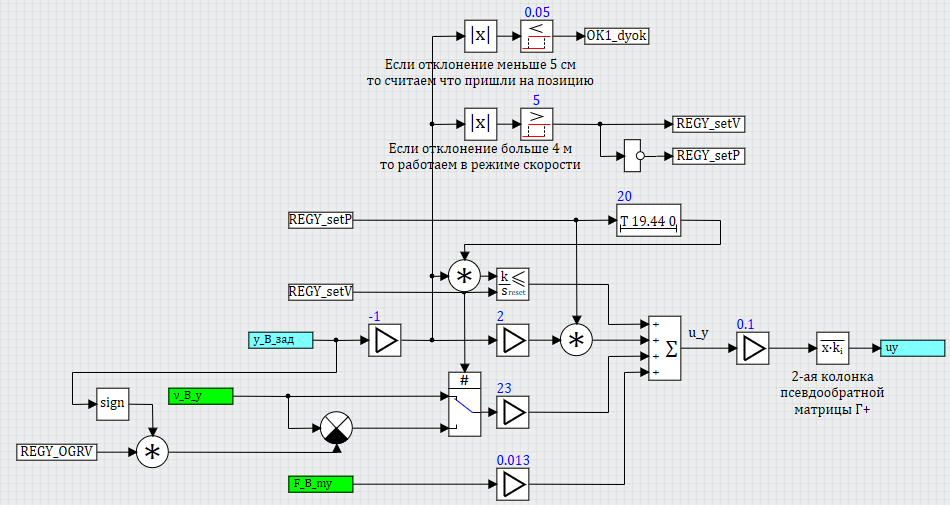
Рисунок 24. Регулятор по каналу Y
Регуляторы двухрежимные, при отклонении от заданной позиции более чем на 5 метров, переключаются в режим работы «V» и поддерживают скорость по направлению на уровне REGX_OGRV (или REGY_OGRV) м/с. При этом, интегрирующая ветка регулятора отключается. При переходе в режим позиции, интегрирующая ветка включается в работу с некоторой задержкой – чтобы коптер успел подлететь к заданной точке и не набралась существенная величина на интеграторе за время «подлета».
Но, отметим еще раз – такой подход будет справедлив и оправдан при существенной управляемости коптера по горизонтальным осям, что может быть достигнуто относительно большим наклоном винтов от вертикальной оси.
Приведенные здесь регуляторы, хотя и кажутся сложными на первый взгляд, являются только лишь базовыми версиями, которые позволяют управлять коптерами. Дальнейшая разработка модели может (и должна) привести к более сложным регуляторам и к повышению качества переходных процессов.
В сумме, на выходе всех 6 каналов управления (по курсу регулятор во многом аналогичен регуляторам ориентации и для сокращения материала не приводим его здесь) мы имеем по каналу регулятора высоты некоторую «базовую» желаемую частоту вращения для каждой из 8 ВМГ, и некоторую «добавку», сформированную остальными 5-ю каналами управления. Единственный нюанс – микшированные добавки, т.к. это не прямая добавка к частоте вращения, а добавка к квадрату частоты вращения, и для того чтобы вычислить добавку именно к частоте вращения, надо еще дополнительно проделать несложные математические вычисления, см. рисунок 25:
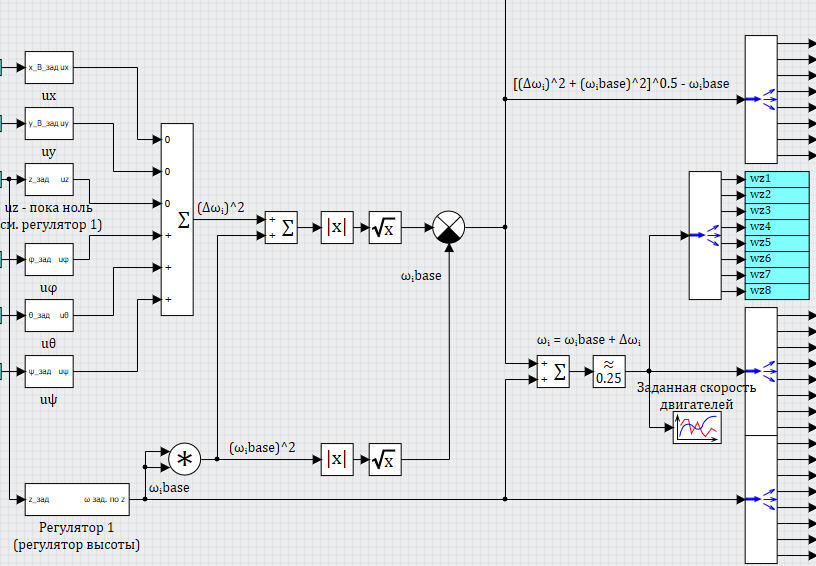
Рисунок 25. Суммирование каналов управления
Сложность вычисления в том, что добавка частоты вращения зависит и от нужного квадрата добавки, и от самой базовой частоты вращения – и чтобы вычислить итоговую частоту вращения как сумму базовой и добавки надо предварительно сделать еще ряд вычислений:
где квадраты скоростей – это сигналы, выходы каналов управления.
Таким образом, в зависимости от текущего уровня «базовой» частоты вращения (которая определяется в основном массой коптера и, возможно, груза и получается на выходе из регулятора высоты), определяется нужная «добавка» угловой скорости для каждой из ВМГ, суммируется с базовой частотой вращения и отправляется как задатчик на регулятор двигателя каждой из ВМГ.
4.6 Регулятор положения коптера в пространстве по каналам крена и тангажа
Опишем кратко подход, который используется для формирования задания по крену и тангажу для того, ��тобы коптер летел в заданном направлении. Для простоты, предположим что курс коптера нулевой (угол ψ равен нулю всегда), тогда для того чтобы коптер двигался вдоль оси X, требуется изменить его угол тангажа θ, а для того чтобы он двигался вдоль оси Y, требуется изменить угол крена.
Путем несложных выкладок, можно получить следующие формулы для вычисления угла наклона:
где и
– рассогласования заданных значений координат и измеренных в инерциальной системе отсчета, а выражения под арксинусом дополнительно ограничиваются некоторой величиной (полученной исходя из запасов управляемости коптера по крену и тангажу), например, диапазоном
.
Если такие величины подать вместо нулевого значения на вход регуляторам крена и тангажа, то регулятор будет дополнительно доворачивать коптер на небольшой угол, для полета вдоль своих осей X и Y. Если учитывать еще и возможность изменения курса, то формулы получатся посложнее, но смысл управления будет тем же самым. Реализация такого управления показана на рисунке 26.
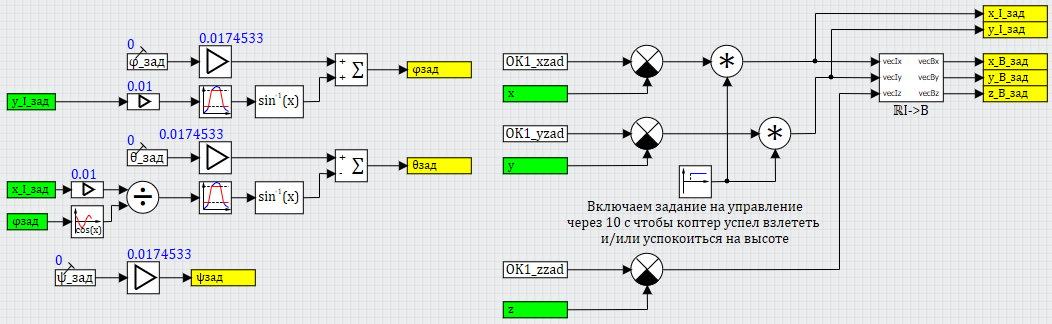
Рисунок 26. Формирование задания на крен и тангаж
Модель коптера можно взять по этой ссылке здесь...:
Видео модели коптера можно посмотреть здесь…
Список литературы
- Первая часть. Введение в моделирование динамики квадро-, гекса- и октокоптеров
- Design, Modeling and Control of an Octocopter, Oscar Oscarson, Royal Institute of Technology 2015
- Development, Modelling and Control of a Multirotor Vehicle, Markus Mikkelsen, Umeå University 2015.
